[알고리즘] Chapter03. 알고리즘(근삿값, 평균, 재귀, 하노이 탑, 병합 정렬, 퀵 정렬)

✍🏻 25일 공부 이야기.

근삿값, 평균, 재귀, 하노이 탑, 병합 정렬, 퀵 정렬 이론을 살펴보았다:)

근사값

• 근사값 : 특정 값에 가장 가까운 값

import random

nums = random.sample(range(0,50),20)
print(f'nums : {nums}')

inputNum = int(input('input number : '))
print(f'inputNum : {inputNum}')

nearNum = 0 #근사값
minNum = 50 #먼저 차이를 선언할 때는 가장 큰 차이(최대값 알고리즘을 이용)로 설정한다.
            #어떠한 차이도 최대값을 넘을 수 없기 때문.

for n in nums: #차이를 계산
  absNum = abs(n - inputNum) #차이
  #print(f'absNum : {absNum}')

  if absNum < minNum: #차이가 기존에 계산된 차이보다 작다면
    minNum = absNum #그 값으로 교체
    nearNum = n #그리고 근사값은 n이 된다.

print(f'nearNum : {nearNum}')

💻 출력

nums : [5, 13, 34, 6, 2, 35, 24, 49, 30, 15, 41, 4, 48, 42, 29, 25, 3, 39, 0, 33]
input number : 20
inputNum : 20
nearNum : 24

강의에서는 위와 같이 알려줬는데, minNum 을 왜 저렇게 설정해야하는지 이해하고 있을 때 하나의 의문이 들었다. 문제에서는 nums 리스트 내의 숫자들 중(즉, 0부터 50사이의 숫자들 내에서만) 특정값과 가까운 값을 찾고자 할 때라는 가정이 있었던 것 같다.

만약 0 미만, 50 초과되는 수의 근사값을 찾고싶다면?

minNum 을 50으로 설정해두었기 때문에 차이가 50을 넘는 수를 입력한다면 아래와 같이 근사값을 제대로 찾지 못한다.

💻 출력

nums : [23, 38, 41, 44, 45, 12, 22, 40, 35, 18, 47, 46, 19, 34, 43, 48, 42, 26, 5, 24]
input number : 150
inputNum : 150
nearNum : 0

그렇다면, 어떠한 수라도 입력하면 근사값을 찾게 해주는 방법은 무엇이 있을까?

나는 최소값 알고리즘을 이용한 방법으로 풀어보았다.

class MinAlgorithm:
  def __init__(self, n):
    self.nums = n
    self.minNum = 0
    self.minNumIdx = 0
  def setMinIdxAndNum(self):
    self.minNum = self.nums[0]
    self.minNumIdx = 0

    for i, n in enumerate(self.nums):
      if self.minNum > n:
        self.minNum = n
        self.minNumIdx = i
  def getMinNum(self):#최소값
    return self.minNum
  def getMinNumIdx(self): #최소값 인덱스
    return self.minNumIdx
    
    
import random

nums = random.sample(range(0,50),20)
print(f'nums : {nums}')

inputNum = int(input('input number : '))
print(f'inputNum : {inputNum}')

absNumList = [] #차이를 담을 리스트

for n in nums: #차이 계산
  absNumList.append(int(abs(n - inputNum))) 
print(f'absNumList : {absNumList}')

'''
이 부분에서 absNumList를 정렬하여 최소값을 찾거나, 
min() 함수를 이용해 최소값을 찾을 수도 있겠지만, 
지금은 함수를 사용하지 않고 하드코딩을 하는 것이 목적이기 때문에 
최소값 알고리즘을 사용해서 풀이해보았다.
'''
findNearNum = MinAlgorithm(absNumList)
findNearNum.setMinIdxAndNum()
minAbs = findNearNum.getMinNum() #차이의 최소값
nearNumIdx = findNearNum.getMinNumIdx() #차이가 최소값인 인덱스
nearNum = nums[nearNumIdx] #근사값

print(f'nums 리스트 숫자들 중 {minAbs}차이로 {inputNum}과의 근사값은 \
{nearNumIdx}번째에 있는 {nearNum}이다.')

💻 출력

nums : [48, 44, 30, 9, 45, 10, 47, 39, 2, 15, 20, 3, 38, 23, 5, 49, 21, 18, 8, 0]
input number : -10
inputNum : -10
absNumList : [58, 54, 40, 19, 55, 20, 57, 49, 12, 25, 30, 13, 48, 33, 15, 59, 31, 28, 18, 10]
nums 리스트 숫자들 중 10차이로 -10과의 근사값은 19번째에 있는 0이다.

💻 출력

nums : [23, 36, 14, 20, 6, 42, 27, 41, 29, 31, 12, 5, 34, 15, 2, 17, 16, 38, 18, 39]
input number : 35
inputNum : 35
absNumList : [12, 1, 21, 15, 29, 7, 8, 6, 6, 4, 23, 30, 1, 20, 33, 18, 19, 3, 17, 4]
nums 리스트 숫자들 중 1차이로 35과의 근사값은 1번째에 있는 36이다.

위 방법을 사용하면 어떤 숫자든 근사값을 찾을 수 있다.

그렇다고 해서 위 알고리즘이 완벽(?)한 것은 아니다. 2번 출력을 보면 35와 가까운 수는 36과 34로 2개가 있는데, 앞서 있는 36이 출력된 것을 볼 수 있다. 위 코드에는 근사값이 2개 이상 있을 때 어떻게 처리할지에 대한 코드는 없기 때문ㅎㅎ

코딩은 항상 문제를 해결해도 예외 상황이 생겨나서 그걸 다시 또 처리해가는 과정이 재밌는 것 같다 :)

평균

• 평균 : 여러 수나 양의 중간값을 갖는 수

어떤 체조선수의 점수의 평균을 구하고 순위를 정하는 알고리즘을 만들어보자.

💡 평균을 계산하고 해당 값이 어디에 들어가야하는지, 들어간다면 기존 값들은 어떻게 이동되는지 생각해보아야 함.

class Top5Players: #상위 5명의 순위를 보여주는 클래스
  def __init__(self, cs, ns): #현재 top5 랭킹과 새로운 스코어를 입력받음
    self.currentScores = cs
    self.newScore = ns
  def setAlignScore(self): #근사값을 이용하여 순위를 정렬하는 알고리즘
    nearIdx = 0 
    nearScore = 0
    minNum = 10.0 #최대 점수가 10.0
    for i, s in enumerate(self.currentScores): #차이 계산
      absNum = abs(self.newScore - s)
      if absNum < minNum:
        minNum = absNum
        nearIdx = i
        nearScore = s
    # 근사값과 근사값 인덱스 찾기 완료

    if self.newScore >= self.currentScores[nearIdx]: #새로운 스코어가 근사값보다 큰 경우
      for i in range(len(self.currentScores)-1, nearIdx, -1): #현재 5위부터 근사값 순위까지의 점수들은
        self.currentScores[i] = self.currentScores[i-1] #하나씩 밀려남(말이 밀려나는 것이지, 현재 5위는 순위표에서 탈락되는 것) 
      self.currentScores[nearIdx] = self.newScore #새로운 스코어를 기존 근사값 자리에 넣어줌
    else: #새로운 스코어가 근사값보다 작은 경우
      for i in range(len(self.currentScores)-1, nearIdx+1, -1):
        self.currentScores[i] = self.currentScores[i-1] #현재 5위부터 (근사값 순위 + 1)위 까지의 점수들은 하나씩 밀려나고
      self.currentScores[nearIdx + 1] = self.newScore #근사값 뒤 자리에 새로운 스코어를 넣어줌

  def getFinalTop5Scores(self):
    return self.currentScores
    
scores = [8.9, 7.6, 8.2, 9.1, 8.8, 8.1, 7.9, 9.4, 7.2, 8.7]
#scores = [8.1,8.1,8.1,8.1,8.1,8.1,8.1,8.1,8.1,8.1]
top5PlayerScores = [9.12, 8.95, 8.12, 7.90, 7.88]
print(f'top5PlayerScores : {top5PlayerScores}')

total = 0; average = 0
for n in scores:
  total += n
average = round((total / len(scores)), 2)
print(f'total : {total}')
print(f'average : {average}')

tp = Top5Players(top5PlayerScores, average)
tp.setAlignScore()
top5PlayerScores = tp.getFinalTop5Scores()
print(f'top5PlayerScores : {top5PlayerScores}')

💻 출력

top5PlayerScores : [9.12, 8.95, 8.12, 7.9, 7.88]
total : 83.9
average : 8.39
top5PlayerScores : [9.12, 8.95, 8.39, 8.12, 7.9]

재귀 알고리즘

• 재귀 : 나 자신을 다시 호출하는 것

반복문 중 일부는 재귀 알고리즘으로 바꿔 사용할 수 있는데, 대표적으로 최대공약수를 구했던 유클리드 호제법이 있다.

이전에 반복문으로 구했던 유클리드 호제법 🖱️링크

def gcd(n1, n2):
  #유클리드 호제법
  #두 자연수 n1, n2(n1 > n2)에 대하여 n1를 n2로 나눈 나머지를 r( = n1 % n2)이라고 할 때,
  #n1과 n2의 최대공약수는 n2와 r의 최대공약수와 같다
  if n1 % n2 == 0:
    return n2
  else:
    #print(f'n1 : {n1}, n2 : {n2}')
    return gcd(n2, n1 % n2)

print(f'gcd(96, 40) : {gcd(96, 40)}')

💻 출력

gcd(96, 40) : 8

하노이의 탑

• 하노이의 탑
  

  세 개의 기둥을 이용해서 원판을 다른 기둥으로 옮기는 퍼즐 게임으로 아래 2가지의 규칙을 따라야한다.

  1. 한 번에 한 개의 원판만 옮길 수 있다.
  2. 큰 원판이 작은 원판 위에 있어서는 안된다.

#하노이탑
#ⅰ. 마지막 원판을 뺀 나머지 원판들을 2번 기둥에 옮기고
#ⅱ. 마지막 원판을 3번 기둥에 옮기고
#ⅲ. 2번 기둥에 있는 나머지 원판들을 3번 기둥에 옮긴다
#ⅰ번과 ⅲ번 과정이 재귀를 이용할 수 있다

def moveDisc(discCnt, fromBar, toBar, viaBar): #원판 개수, 1번 기둥, 3번 기둥, 2번 기둥
  if discCnt == 1:
    print(f'{discCnt}disc를 {fromBar}에서 {toBar}(으)로 이동!')
  else:
    #ⅰ(discCnt-1)개 원판들을 2번 기둥으로 이동
    moveDisc(discCnt -1, fromBar, viaBar, toBar)

    #ⅱ마지막 원판를 3번 기둥으로 이동
    print(f'{discCnt}disc를 {fromBar}에서 {toBar}(으)로 이동!')

    #ⅲ(discCnt-1)개 원판들을 3번 기둥으로 이동
    moveDisc(discCnt -1, viaBar, toBar, fromBar)

moveDisc(3,1,3,2)

💻 출력

1disc를 1에서 3(으)로 이동!
2disc를 1에서 2(으)로 이동!
1disc를 3에서 2(으)로 이동!
3disc를 1에서 3(으)로 이동!
1disc를 2에서 1(으)로 이동!
2disc를 2에서 3(으)로 이동!
1disc를 1에서 3(으)로 이동!

병합 정렬

• 병합 정렬 : 자료구조를 분할하고 각각의 분할된 자료구조를 정렬한 후 다시 병합하여 정렬하는 방법.

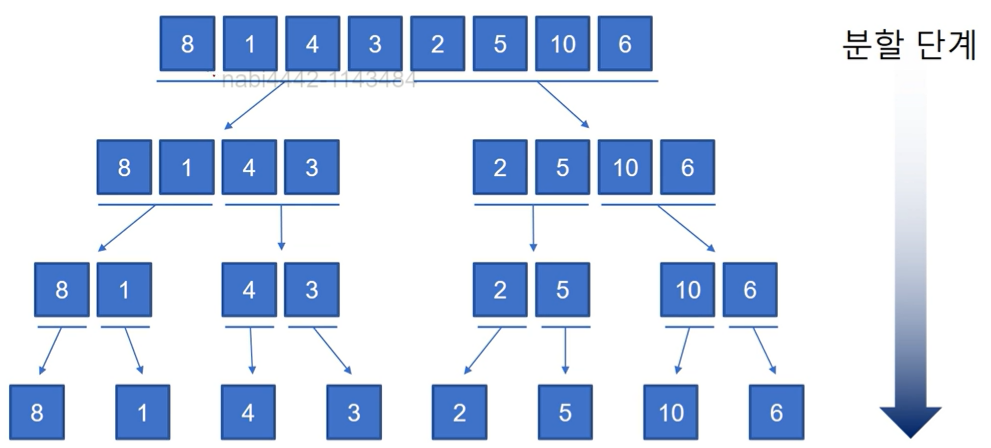
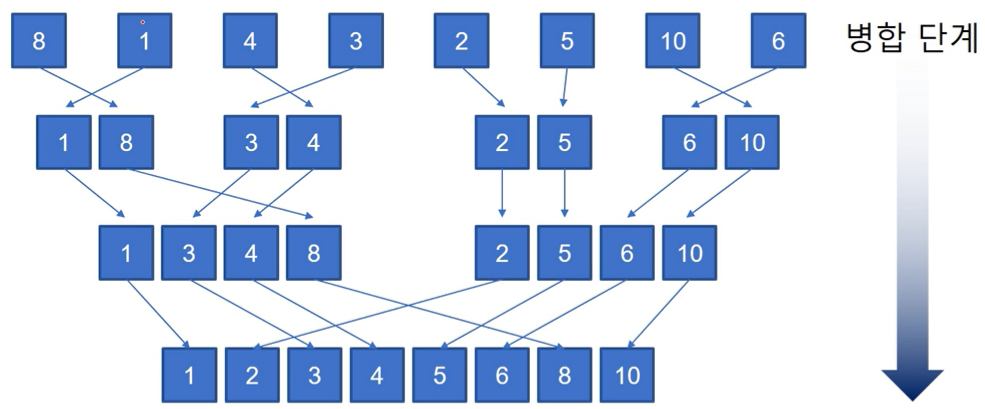
크고 작음을 비교해서 자리 바꿈을 하며 병합함

def mergeSort(ns): #만약 오름/내림차순 옵션을 넣는다면 
				   #(1) 부분도 같이 옵션을 넣어주어야함(재귀)

  #분해하는 단계 완료됨 
  if len(ns) < 2 : 
    return ns 
  #중간 인덱스를 구해서 자료구조들을 분해함
  midIdx = len(ns) // 2 #소수점은 버림함
  leftNums = mergeSort(ns[:midIdx]) #(1)
  rightNums = mergeSort(ns[midIdx:]) #(1)

  #병합하는 단계
  mergeNums = []
  leftIdx = 0; rightIdx = 0
  # print(f'leftNums : {leftNums}')
  # print(f'rightNums : {rightNums}')
  # print('******************************')
  while leftIdx < len(leftNums) and rightIdx < len(rightNums):
    #반으로 나누고 정렬한 후, 맨 앞 원소들끼리 비교
    #기준에 맞는 값을 재위치시킴
    #두 리스트를 다 검사할 때까지 아래 코드 실행
    # print(f'leftNums : {leftNums[leftIdx]} , rightNums : {rightNums[rightIdx]}')
    if leftNums[leftIdx] < rightNums[rightIdx]: #왼쪽 수 < 오른쪽 수 이면 
      mergeNums.append(leftNums[leftIdx]) #작은 왼쪽 수를 먼저 정렬 리스트에 넣어줌
      leftIdx += 1 #왼쪽 인덱스를 늘려가며 다시 검사
    else:#왼쪽 수 > 오른쪽 수 이면
      mergeNums.append(rightNums[rightIdx]) #작은 오른쪽 수를 먼저 정렬 리스트에 넣어줌
      rightIdx += 1 #오른쪽 인덱스를 늘려가며 다시 검사 
  # print(f'mergeNums : {mergeNums}')
  # print('******************************')
  mergeNums = mergeNums + leftNums[leftIdx:] + rightNums[rightIdx:] #정렬된 값과 나머지 값들을 합쳐줌
            #작은수들이 미리 정렬된 mergeNums 먼저
  print(f'mergeNums : {mergeNums}')
  return mergeNums

nums = [8,1,4,3,2,5,10,6]
print(f'merge sort nums : {mergeSort(nums)}')

💻 출력

mergeNums : [1, 8]
mergeNums : [3, 4]
mergeNums : [1, 3, 4, 8]
mergeNums : [2, 5]
mergeNums : [6, 10]
mergeNums : [2, 5, 6, 10]
mergeNums : [1, 2, 3, 4, 5, 6, 8, 10]
merge sort nums : [1, 2, 3, 4, 5, 6, 8, 10]

퀵 정렬

• 퀵 정렬 : 기준값보다 작은 값과 큰 값으로 분리한 후 다시 합쳐서 정렬하는 방법.
  

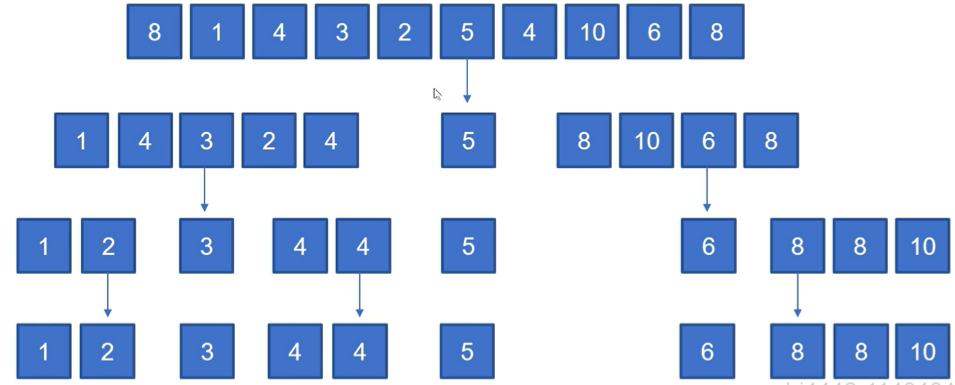
def qSort(ns):
  if len(ns) < 2:
    return ns
  
  #중앙값을 기준점으로 잡음
  midIdx = len(ns) // 2
  midVal = ns[midIdx]

  smallNums = []; sameNums = []; bigNums = []
  # print(f'nums : {ns}')
  for n in ns:
    #기준값과 비
    if n < midVal:
      smallNums.append(n)
    elif n == midVal:
      sameNums.append(n)
    else:
      bigNums.append(n)
  
  # print(f'smallNums : {smallNums}')
  # print(f'sameNums : {sameNums}')
  # print(f'bigNums : {bigNums}')

  return qSort(smallNums) + sameNums + qSort(bigNums)

nums = [8,1,4,3,2,5,4,10,6,8]
print(f'quick sort nums : {qSort(nums)}')

💻 출력

quick sort nums : [1, 2, 3, 4, 4, 5, 6, 8, 8, 10]