DP? (Dynamic Programming)

function fibMemo(n, memo = []) {
    if(memo[n] !== undefined) return memo[n];
		// 이미 해결한 하위 문제인지 찾아본다
    if(n <= 2) return 1;
    let res = fibMemo(n-1, memo) + fibMemo(n-2, memo);
		// 없다면 재귀로 결과값을 도출하여 res 에 할당
    memo[n] = res;
		// 추후 동일한 문제를 만났을 때 사용하기 위해 리턴 전에 memo 에 저장
    return res;
}

가장 큰 문제를 방문 후 작은 문제를 호출하여 답을 찾는 방식이다.
재귀호출을 통해 값을 구하고 구한 값을 배열에저장하는 Memoization방식을 사용한다.

Bottom-up(Iteration + Tabulation)

function fibTab(n) {
    if(n <= 2) return 1;
    let fibNum = [0, 1, 1];
		// n 이 1 & 2일 때의 값을 미리 배열에 저장해 놓는다
    for(let i = 3; i <= n; i++) {
        fibNum[i] = fibNum[i-1] + fibNum[i-2];
		// n >= 3 부터는 앞서 배열에 저장해 놓은 값들을 이용하여
		// n번째 피보나치 수를 구한 뒤 배열에 저장 후 리턴한다 
    }
    return fibNum[n];
}

가장 작은 문제들 부터 답을 구해가며 전체 문제의 답을 찾는 방식이다.
반복문을 이용해서 답을 구한다.

차이점

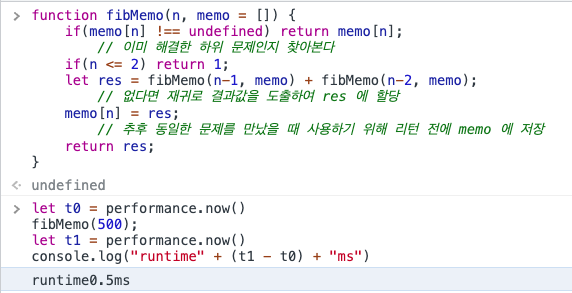
먼저 Top-down은 input이 500이 주어질때 0.5ms의 퍼포먼스를 보여준다.

반면 Bottom-up은 동일한 inputdl 주어질때 평균 0.2ms의 퍼포먼스를 보여준다.

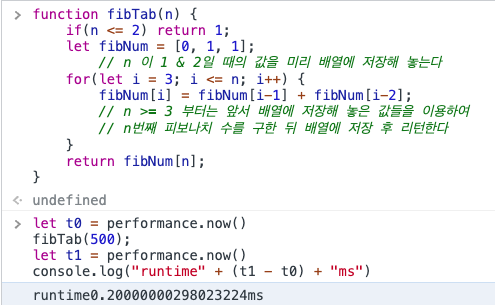
왜 차이가 날지에 대해서 고민해봤다. Top-down방식은 함수를 재귀호출하고 있다. 반면에 Bottom-up방식은 함수를 재귀호출 하고 있지 않기 때문에 시간과 메로리 사용량이 줄어든 것으로 보여진다.

고민

알고리즘을 구현할때 가독성때문에 재귀호출방식을 자주 사용했었다. 하지만 재귀호출방식으로는 런타임아웃이 뜨는 문제가 여럿 있었고, 같은 코드를 반복문으로 바꿔서 적용했을때는 통과하는 경우가 많았다. 예상하기로 함수를 다시 호출한다는 것이 시간과 공간복잡도를 더 사용한다라고 생각했었는데 이번 블로깅을 통해 이해할 수 있었다. 하지만 Bottom-up방식의 dp는 생각해내기가 너무 어려운것 같다.

황순은

안녕하세요.

이전 포스트