순환 신경망(RNN)

기존의 신경망 구조는 정해진 입력 $x$를 받아 $y$를 출럭해주는 형태였습니다. 하지만 순환 신경망(RNN)은 입력$x_1$와 직전의 은닉상태(hidden state)인 $h_{t-1}$를 참조하여 현재의 상태인 $h_t$를 결정하는 작업을 여러 time-step에 걸쳐 수행합니다. 각 time-step별 RNN의 은닉 상태는 경우에 따라 출력값이 될 수 있습니다.
RNN을 수식으로 표현하면 $h_t = f(x_t,h_{t-1};\theta)$입니다.

피드 포워드

기본적인 RNN을 활용한 피드포워드 계산의 흐름을 살펴보겠습니다.

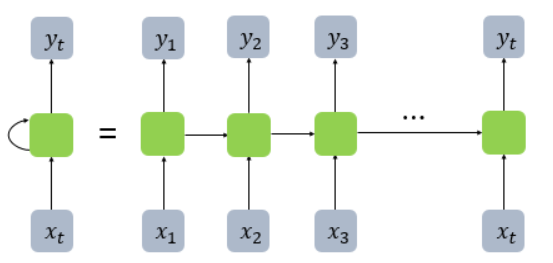
위의 그림과 같이 각 time-step별로 입력 $x_t$와 $h_{t-1}$이 RNN으로 들어가서 $\widehat{y_t}$을 출력합니다. 이후 정답인$y_t$와 비교하여 손실 $L$을 계산합니다. 위 그림을 수식으로 나타내면 아래와 같습니다.

입력 $x_t$를 입력받아서 입력에 대한 가중치 $W_{ih},b_{ih}$를 곱하고 더한후, 함께 입력으로 받은 $h_{t-1}$과 가중치 $W_{hh},b_{hh}$를 곱하고 더한 값을 모두 더해줍니다. 이후에 활성화 함수 $tanh$를 거쳐 현재의 은닉상태 $h_t$를 반환합니다.

최종적으로 time-step별 $y_t$를 계산하여 모든 time-step에 대한 손실$L$을 구한 후, time-step의 수만큼 평균 냅니다.

RNN의 입력 텐서와 은닉 상태 텐서의 크기

이때 입력으로 주어지는 $x_t$의 미니배치까지 감안한 크기는 다음과 같습니다.

파이토치의 텐서에 대해 size() 함수를 호출했을떄 반환되는 튜플값과 같은 표현입니다. (batch_size, 1 , input_size)

텐서에서 batch_size의 숫자는 미니배치에서 샘플 인덱스를 나타내며, input_size의 숫자는 미리 정해진 입력벡터의 차원(예를 들면 임베딩 계층의 출력 벡터의 차원 수)를 나타냅니다. 두번째 숫자인 1은 시퀀스 내에서 현재 time-step의 인덱스를 나타냅니다. 그럼 n개의 time-step을 가진 전체 시퀀스는 (batch_size, n, input_size)로 나타납니다.

BPTT

이렇게 순전파된 이후에 역전파 과정을 거칩니다.
각 time-step의 RNN에 사용된 파라미터 $\theta$는 모든 시간에 공유되어 사용됩니다. 따라서 앞서 구한 손실 $L$에 미분을 통해 역전파를 수행하게 되면, 각 time-step별로 뒤로부터 $\theta$의 기울기가 구해지고, 이전 time-step(t-1)$\theta$의 기울기에 더해집니다. 즉, t가 0에 가까워 질수록 RNN 파라미터 $\theta$의 기울기는 각 time-step별 기울기가 더해져 점점 커집니다.

이런 RNN의 속성을 '시간 축에 대해서 수행되는 역전파 방법'이란 뜻으로 BPTT라고 합니다. 이런 속성으로 인해 RNN은 마치 time-step 수만큼 계층이 존재하는 것과 마찬가지인 상태가 됩니다.

기울기 소실

그런데 앞의 RNN의 수식을 보면 활성화 함수로 tanh함수가 사용됩니다.

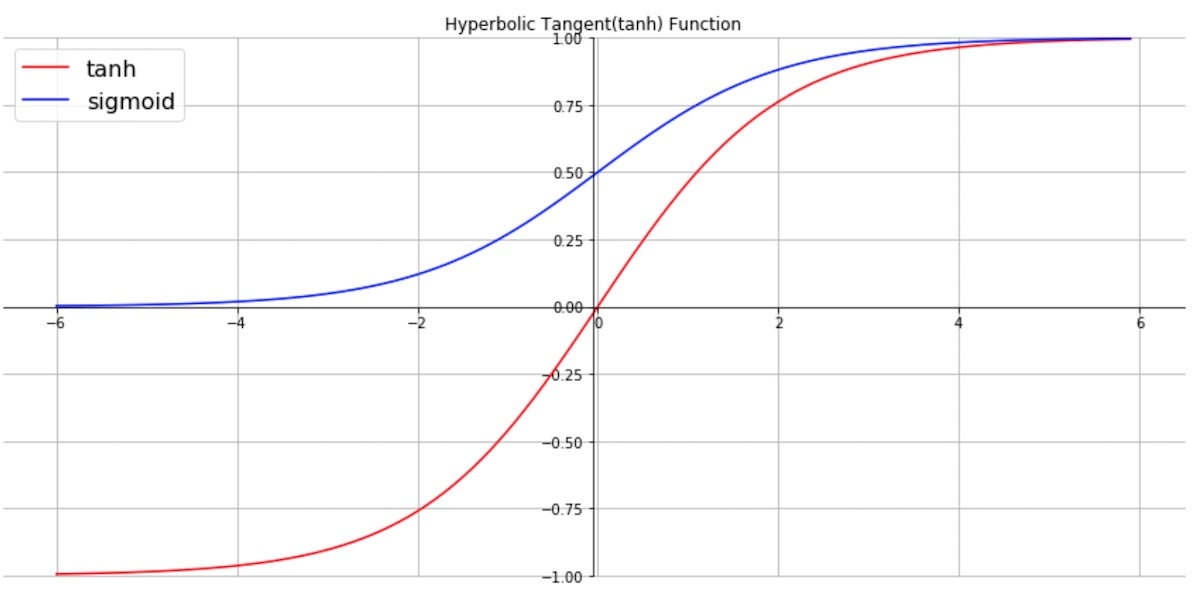
빨간선이 tanh, 파란색이 sigmoid 함수입니다. 그래프를 보면 tanh의 양 끝 기울기가 점차 0에 가까워 집니다. 따라서 양 끝 값을 반환하는 층의 경우 기울기가 0에 가까워지고, 그 다음으로 미분 값을 전달받는 계층은 제대로 된 미분 값(기울기)을 전달 받을 수 없게 됩니다.

이를 기울기 소실이라고 합니다. 따라서 RNN과 같이 time-step이 많거나, RNN이 아니더라도 여러 계층 구조를 갖는 다층 퍼셉트론(MLP)의 경우 기울기 소실 문제가 쉽게 발생합니다. 최근에는 ReLU와 레지듀얼 커넥션으로 해결 가능합니다.

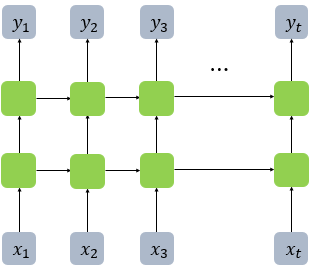
여러 계층을 갖는 RNN

RNN은 하나의 time-step 내에서 여러 층의 RNN을 쌓아올릴 수도 있습니다. 이렇게 되면 층별로 파라미터 $\theta$를 공유하지 않고 따로 가집니다. 각 층 사이에 드롭아웃(dropout)을 끼워 넣기도 합니다.

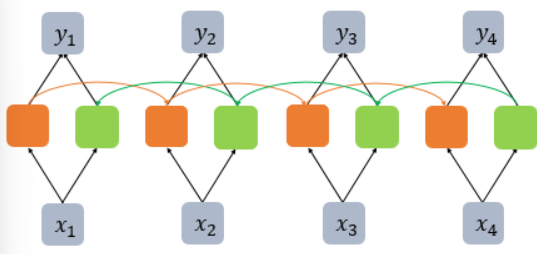
양방향 RNN

앞에서 이야기한 RNN은 time-step을 1부터 마지막 time-step에 이르기까지 차례로 입력받아 진행했습니다. 하지만 양방향 RNN을 사용하면 기존의 정방향에 역방향이 추가되어 마지막 time-step에서부터 거꾸로 역방향으로 입력받아 진행합니다. 이 경우에도 정방향과 역방향은 $\theta$를 공유하지 않습니다.

자연어 처리에 RNN을 적용하는 사례

RNN의 입출력은 기본적으로 다음과 같이 분류할 수 있습니다.

입력	출력	비고
다수	단일	many to one
다수	다수	many to many
단일	다수	one to many

하나의 출력을 사용할 경우

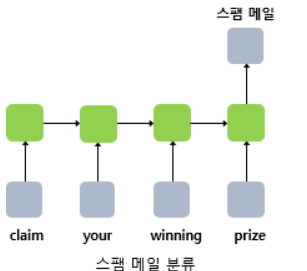
가장 대표적인 사례가 텍스트 분류 예제입니다.
이때 단어(토큰)의 개수만큼 입력이 RNN에 들어가고, 마지막 time-step의 결괏값을 받아서 softmax 함수를 통해 해당 입력 텍스트의 클래스를 예측하는 확률 분포를 근사하도록 동작합니다.

자연어 처리에서 단어는 불연속적인 값을 지닙니다. 따라서 이때 각 time-step별 입력 단어인 $x_t$는 불연속적인 이산 분포로 부터 샘플링된 샘플입니다. $x_t$는 원 핫 벡터로 표현되고, 임베딩 계층을 거쳐 정해진 차원의 단어 임베딩 벡터인 덴스 벡터로 표현되어 RNN에 입력으로 주어집니다. 정답 또한 불연속적 값인 단어 또는 클래스가 될 것입니다. 따라서 우리는 softmax 함수를 통해 멀티눌리 확률 분포를 표현합니다. 또한 원래의 정답도 원핫 벡터가 되어 교차 엔트로피 손실함수를 통해 softmax 결괏 값 벡터와 비교하여 손실값을 구하게 됩니다.

모든 출력을 사용할 경우

여전히 입력은 불연속적인 값이 될 것이고, 출력 또한 불연속적인 값이 될 것 입니다. 따라서 다음 그림과 같이 각 time-step별로 불연속적 샘플인 원핫 베거를 입력으로 받아 임베딩 계층을 거쳐 덴스 벡터를 만들어 RNN을 거치고, RNN은 time-step별로 결과물을 출력한 뒤, time-step별로 softmax함수를 거쳐 이산확률 분포의 형태로 만듭니다. 이후 불연속적인 원핫 벡터로 구성된 정답과 비교하여 손실을 구합니다.

LSTM

RNN은 가변길이의 시퀀셜 데이터 형태 입력에는 휼륭하게 동작하지만, 그 길이가 길어지면 앞서 입력된 데이터를 잊어버리는 치명적인 단점이 있습니다. 하지만 LSTM(long short-term memory)의 등장으로 RNN의 단점을 보완할 수 있게 되었습니다.

LSTM은 기존 RNN의 은닉 상태 이외에도 별도의 셀 스테이트(cell state)라는 변수를 두어 그 기억력을 증가시킵니다. 그뿐아니라 여러가지 게이트(gate)를 둠으로써 기억하거나, 잊어버리거나, 출력하고자 하는 데이터의 양을 상황에 따라 마치 수도꼭지를 잠갔다가 열듯이 효과적으로 제어합니다. 그 결과 긴 길이의 데이터에 대해서도 효율적으로 대체할 수 있게 되었습니다. 다음은 LSTM의 수식입니다.

여기서 $W$는 전부 가중치를 의미합니다.

입력 게이트

$i_t = \sigma(W_{ii}x_t + b_{ii}, W_{hi}h_{t-1} + b_{hi})$
$g_t = tanh(W_{ig}x_t + b_{ig}+ W_{hg}h_{t-1} + b_{hg})$
입력 게이트는 현재 정보를 기억하기 위한 게이트입니다. 현재 시점 t의 x값과 입력 게이트로 이어지는 가중치 $W_{ii}$를 곱한 값과 이전 시점 t-1의 은닉 상태가 입력 게이트로 이어지는 가중치 $W_{hi}$를 곱한 값을 더한 뒤 시그모이드를 지납니다. 그리고 현재시점 t의 x값과 입력 게이터로 이어지는 가중치 $W_{ig}$를 곱한 값과 이전 시점 t-1의 은닉 상태가 입력 게이트로 이어지는 가중치 $W_{hg}를 곱한 값을 더하여 tanh를 지납니다.

삭제 게이트

$f_t = \sigma(W_{if}x_t + b_{if}, W_{hf}h_{t-1} + b_{hf})$
삭제 게이트는 기억을 삭제하기 위한 게이트입니다. 현재시점의 x값과 이전 시점의 은닉상태가 시그모이드 함수를 지나게 됩니다. 그 결과로 0에서 1 사이의 값이 나오는데 0에 가까울수록 많은 정보가 삭제된 것입니다.

셀 스테이트(cell state)

$c_t = f_t{\displaystyle \bigcirc }c_{t-1}+i_t{\displaystyle \bigcirc }g_t$
입력 게이트에서 구한 $i_t, g_t$ 이 두 개 의 값에 대해서 원소 곱(아다마르 곱)을 진행합니다. 이 값이 이번에 기억할 값입니다. 입력 게이트에서 선택된 기억을 삭제 게이트의 결과값과 더합니다. 이 값을 현재 시점의 t의 셀 스테이트(cell state)라고 하며, 이 값은 다음 t+1 시점의 LSTM 셀로 넘겨집니다.

출력 게이트와 은닉상태

출력 게이트는 현재 시점 t의 x값과 이전 시점 t-1의 은닉 상태가 시그모이드 함수를 지난 값입니다. 해당 값은 현재 시점 t의 은닉 상태를 결정하는데 쓰이게 됩니다. 셀 스테이트의 값이 tanh 함수를 지나 -1에서 1사이의 값이 되고, 해당 값은 출력 게이트의 값과 연산되면서, 값이 걸러지는 효과가 발생해 은닉상태가 됩니다. 이 은닉 상태의 값 역시 출력층로 향합니다.

GRU

GRU(gated recurrent unit)는 LSTM의 간소화 버전입니다. 기존 LSTM이 복잡한 모델인 데 비해 더 간단한? 버전입니다.

GRU 또한 LSTM과 마찬가지로 시그모이드 $\sigma$로 구성된 리셋 게이트 $r_t$아 업데이트 게이트$z_t$가 있습니다.

GRU는 LSTM 대비 더 가벼운 몸집이지만 아직까지는 LSTM을 사용하는 빈도가 더 높습니다.