📌 딥러닝이란?

1980년대 (1950) 부터 신경망(Neural Networks)이 인기를 끌기 시작하여, NeurIPS, Snowbird 같은 훌륭한 학회들과 더불어 많은 성공 사례와 큰 기대를 모았다.

1990년대에 다양한 기법들이 등장하면서 뒷전으로 밀렸지만, 2010년 경 "딥러닝"으로 부활하여 현재는 매우 지배적인 분야이다.

성공 배경에는 Computing Power, Larger Training Sets, PyTorch, Tensorflow

---

📌 PyTorch vs. Tensorflow

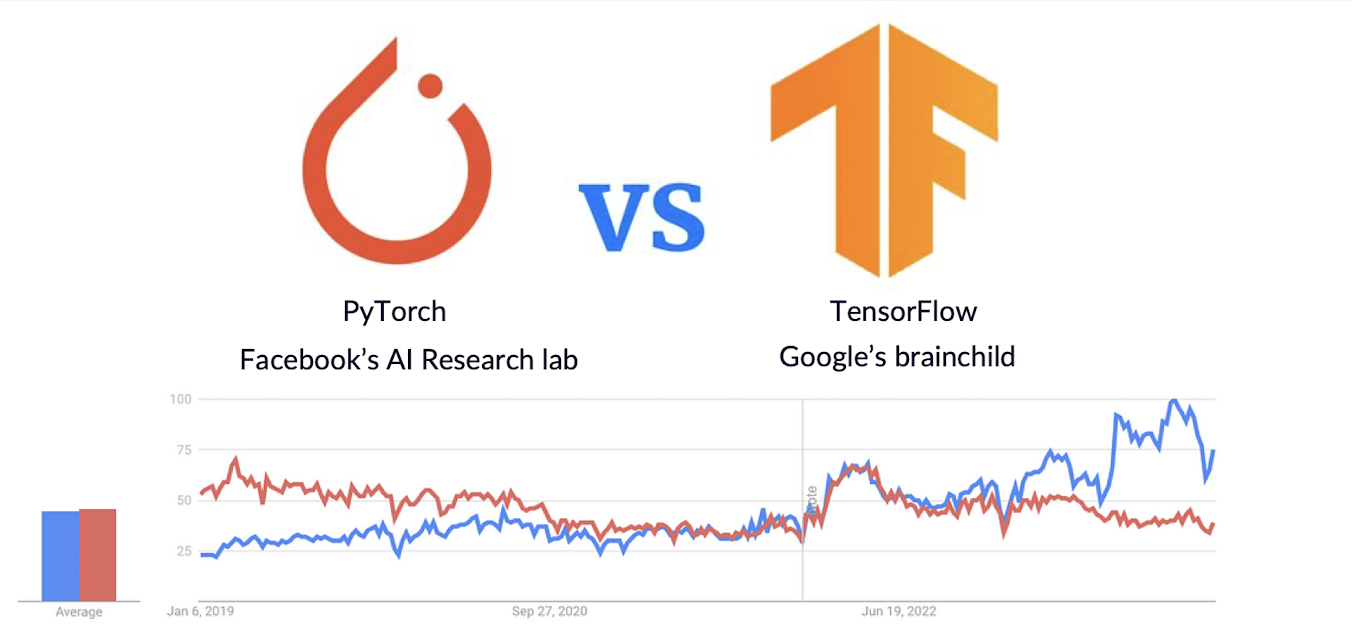
PyTorch

• 간편하고 유연성이 좋으며 Pythonic(파이썬과의 연계)하다.
• 초보자와 연구자들이 많이 사용

Tensorflow

• 구조적인 접근 '정적 계산 그래프(static computation graph)'를 사용하여 사전에 계획이 필요하다.
• 처음부터 구조적인 생태계를 고려하여 개발할 경우 사용하면 고성능 모델 개발에 유리하다.

---

Single Layer Neural Network

✔️ 단일 계층 신경망을 통한 Y 예측

• 𝑌 = 𝑓(𝑋) → 목표는 입력 𝑿로부터 결과 𝒀를 예측하는 것.

• 𝑌: 반응 변수 (예측하고자 하는 값)

• 𝑋 = (𝑋₁, … , 𝑋ₚ): 입력 벡터, 총 p개의 변수로 구성됨

• 𝑓(𝑋): 입력 𝑿에 대한 비선형 함수, 학습을 통해 추정됨

파라미터의 개수
$parameters: (p+1) \cdot K + (K + 1)$ 는 다음과 같다. → $W_{kj} + \beta_k$

✔️ 단일 계층 신경망(Single Layer Neural Network) 모델

• 함수 형태:

  $f(X) = \beta_0 + \sum_{k=1}^{K} \beta_k h_k(X)$

• 이때, 각 은닉 유닛 $h_k(X)$ 는 다음과 같이 계산됨:

  $h_k(X) = g\left(w_{k0} + \sum_{j=1}^{p} w_{kj} X_j \right)$

• 전체를 다시 쓰면:

  $f(X) = \beta_0 + \sum_{k=1}^{K} \beta_k \cdot g\left(w_{k0} + \sum_{j=1}^{p} w_{kj} X_j \right)$

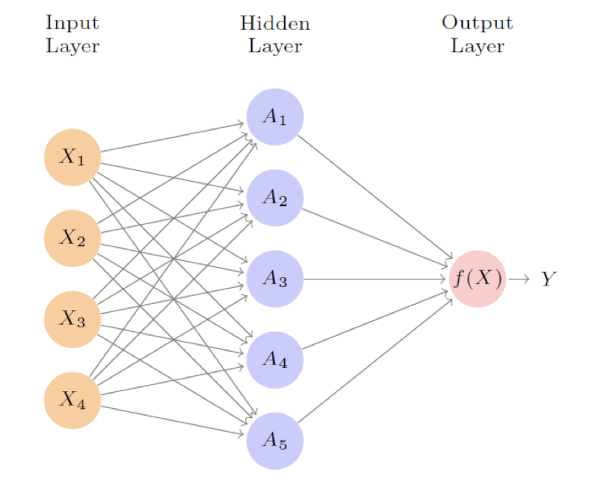
📌 구성 요소 설명
K: 은닉 유닛(hidden units)의 개수
𝑔(z): 사전에 정의된 비선형 활성화 함수 (예: ReLU, sigmoid, tanh 등)
𝑤ₖⱼ: 은닉층의 가중치
𝛽₀, 𝛽ₖ: 출력층의 바이어스와 가중치

---

Activation Function

$A_k = h_k(X) = g\left(w_{k0} + \sum_{j=1}^{p} w_{kj} X_j \right)$ 는 은닉층에서의 활성값(activation) 이라고 불린다.

여기서 $g(z)$ 는 활성화 함수(activation function) 라고 한다.

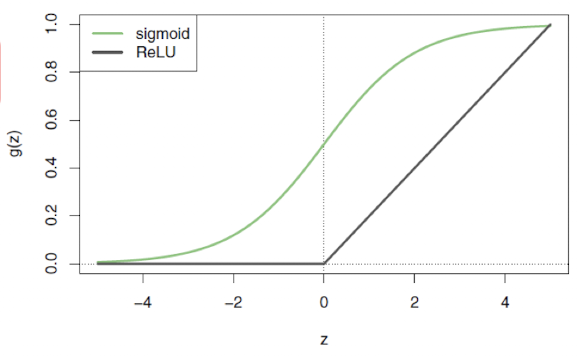
자주 사용되는 활성화 함수로는 시그모이드(Sigmoid) 와 ReLU(Rectified Linear Unit) 가 있다.

Sigmoid 함수

출력값은 항상 0과 1 사이이며, 확률처럼 해석할 수 있다.

ReLU 함수

입력이 0보다 작으면 0을 출력하고, 0 이상이면 그대로 출력한다.

ReLU 함수는 시그모이드보다 계산 효율이 높기 때문에, 최근의 신경망 모델에서는 ReLU가 기본 활성화 함수로 널리 사용된다.

🔍 은닉층의 활성화 함수와 비선형성

은닉층에서의 활성화 함수는 일반적으로 비선형이다.
만약 활성화 함수가 선형이라면, 전체 신경망 모델은 결국 선형 모델로 수렴하게 된다.
(즉, 은닉층을 쌓는 의미가 사라진다.)

✅ 모델 수식

‼️ 예시: 이차 함수(quadratic function)를 활성화 함수로 사용할 경우 (비선형이지만 매우 단순한 형태)

• 입력 $X = (X_1, X_2)$
• 은닉 유닛 수: $K = 2$
• 활성화 함수: $g(z) = z^2$

• 가중치 및 계수:
  $\beta_0 = 0,\quad \beta_1 = \frac{1}{4},\quad \beta_2 = -\frac{1}{4}$
  $w_{10} = 0,\quad w_{11} = 1,\quad w_{12} = 1$
  $w_{20} = 0,\quad w_{21} = 1,\quad w_{22} = -1$

• 은닉 유닛 계산:
  $h_1(X) = (0 + X_1 + X_2)^2 = (X_1 + X_2)^2$
  $h_2(X) = (0 + X_1 - X_2)^2 = (X_1 - X_2)^2$

• 최종 출력:
  $f(X) = \frac{1}{4}(X_1 + X_2)^2 - \frac{1}{4}(X_1 - X_2)^2 = X_1 X_2$

즉, 결과는 입력 간 상호작용(interaction term) 을 나타내는 항이지만, 여전히 선형 모델이다!

✅ 모델학습
신경망 모델은 다음 손실 함수를 최소화하여 학습된다. (예: 회귀 문제):

Multilayer Neural Network

현대의 신경망(Modern Neural Networks)은 일반적으로 하나 이상의 은닉층(hidden layer)을 가진다.

적당한 크기의 여러 은닉층을 쌓는 것이 훨씬 더 좋은 해법을 찾는 데 용이하다.
즉, 다층 구조(multi-layer structure)가 학습을 더 효율적이고 효과적으로 만든다.

🔢 MNIST 숫자 인식 (MNIST Digits)

• MNIST: 손글씨 숫자 (0~9) 이미지 데이터셋

• 28 × 28 크기의 흑백 이미지, 총 784개의 픽셀

• 픽셀 값은 0~255 범위의 정수값 (학습용 60,000장, 테스트용 10,000장)

• 입력 벡터:

  $X = (X_1, X_2, \dots, X_{784}), \quad X_j \in (0, 255)$

• 출력 벡터 (one-hot 인코딩된 더미 변수 임 → 10개중 하나만 1):

  $Y = (Y_0, Y_1, \dots, Y_9)$

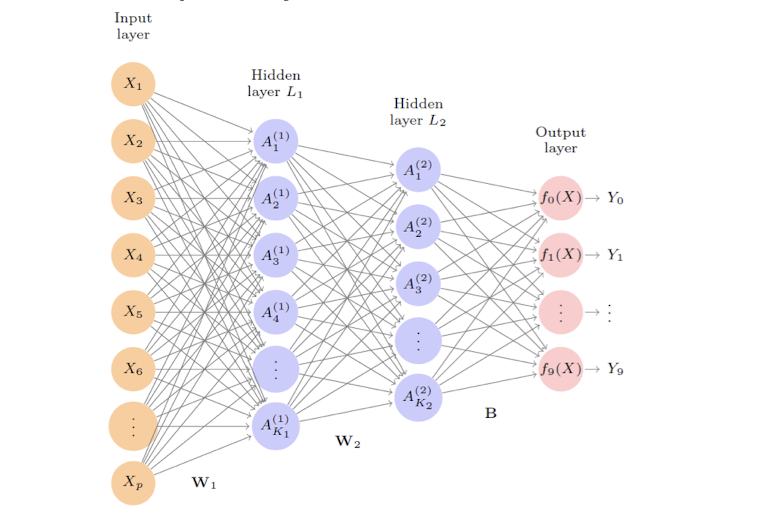
🖇️ 1층 은닉층 ($L_1$: 256 유닛)

은닉 유닛 계산:

가중치 행렬 $𝑊^{(1)}$ 크기:

🖇️ 2층 은닉층 ($L_2$: 128 유닛)

은닉 유닛 계산:

가중치 행렬 $𝑊^{(2)}$ 크기:

🖇️ 출력층 (10개 유닛)

선형 결합:

가중치 행렬 $B$ 크기:

전체 파라미터 수 (bias 포함):

✅ 출력층 활성화 함수: Softmax

멀티클래스 로지스틱 회귀와 동일한 방식
10개의 확률값은 0 이상이며 합이 1, 가장 높은 확률의 클래스를 최종 예측

✅ 학습: 손실 함수 (Cross-Entropy)

• $y_{im} =1$: 정답이 클래스 $𝑚$ 일 때만 $1$, 나머지는 $0$ (one-hot encoding)

negative log-likelihood를 최소화하기 위함

✅ 테스트 에러율과 정규화

많은 파라미터 수 → 정규화(regularization)가 필수
사용된 정규화 방식: 릿지(Ridge), 드롭아웃(Dropout)
최고의 모델은 에러율 0.5% 미만 달성 (인간의 에러율은 약 0.2% (테스트 이미지 10,000장 중 20개 오류))

2D Tensor: (#Samples, #Features)