저는 해당 책을 보고 개념을 정리하였습니다.

- 모두의 딥러닝
Gradient descent
경사 하강법은 반복적으로 기울기 a를 변화 시켜서 m의 값을 찾아내는 방법이다. 즉, 오차의 변화에 따라 이차 함수 그래프를 만들고 적절한 학습률을 설정해 미분 값이 0인 지점을 구하는 것을 말한다.
Back propagation
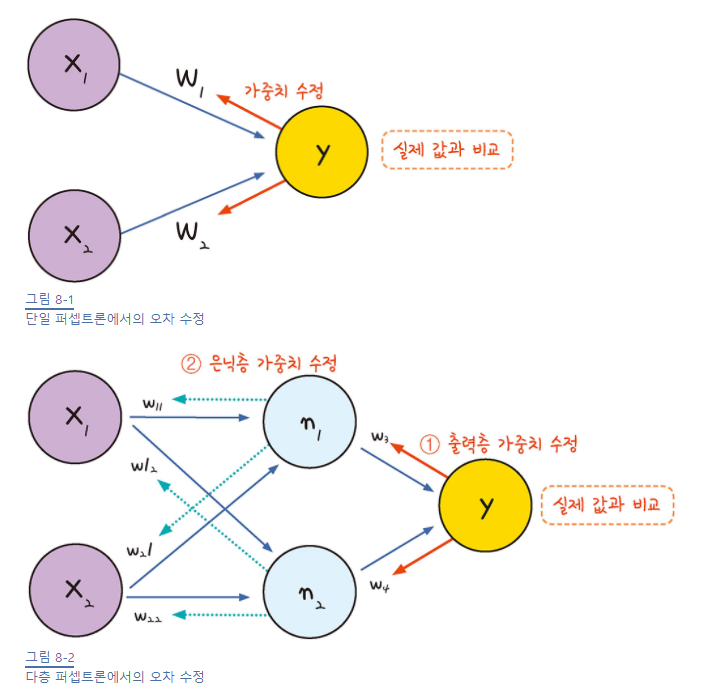
단일 퍼셉트론에서 결괏값을 얻으면 오차를 구해 이를 토대로 앞 단계에서 정한 가중치를 조정하는 것과 마찬가지로, 다층 퍼셉트론 역시 결괏값의 오차를 구해 이를 토대로 하나 앞선 가중치를 차례로 거슬러 올라가며 조정해 갑니다.
- output layer의 가중치 수정
- hidden layer의 가중치 수정
그러다 보니 최적화의 계산 방향이 출력층에서 시작해 앞으로 진행됩니다. 그래서 다층 퍼셉트론에서의 최적화 과정을 오차 역전파(back propagation)이라 부릅니다.
구성
오차 역전파의 구동 방식은 다음과 같습니다.
- 임의의 초기 가중치(W)를 준 뒤 결과(y_out)을 계산한다.
- 계산 결과와 우리가 원하는 값 사이의 오차를 구한다.
- 경사 하강법을 이용해 바로 앞 가중치를 오차가 작아지는 방향으로 업데이트한다.
- 위 과정을 더이상 오차가 줄어들지 않을 때까지 반복한다.
여기서 '오차가 작아지는 방향으로 업데이트한다'는 의미는 미분 값이 0에 가까워지는 방향으로 나아간다는 말입니다. 즉, '기울기가 0이 되는 방향'으로 나아가야 하는데, 이 말은 가중치에서 기울기를 뺐을 때 가중치의 변화가 전혀 없는 상태를 말합니다.
따라서 오차 역전파를 다른 방식으로 표현하면 가중치에서 기울기를 빼도 값의 변화가 없을 때까지 계속해서 가중치 수정 작업을 반복하는 것입니다.
W(t+1) = Wt -
코딩으로 설계
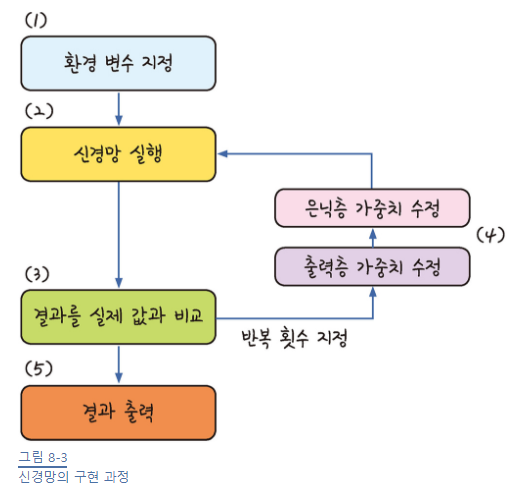
- 환경 변수 지정 | 환경 변수에는 입력값과 타겟 결괏값이 포함된 데이터셋, 학습률 등이 포함됩니다, 또한, 활성화 함수와 가중치 등도 선언되어야 합니다.
- 신경망 실행 | 초깃값을 입력하여 활성화 함수와 가중치를 거쳐 결괏값이 나오게 합니다.
- 결과를 실제 값과 비교 | 오차를 측정합니다.
- 역전파 실행 | 출력층과 은닉층의 가중치를 수정합니다.
- 결과 출력
오차역전파의 계산법
1. 출력층의 오차 업데이트
각 노드 내부에서는 입력 값을 이용해 가중합을 만드는 단계와 이 가중합을 활성화 함수를 적용해 출력하는 단계로 구분됩니다
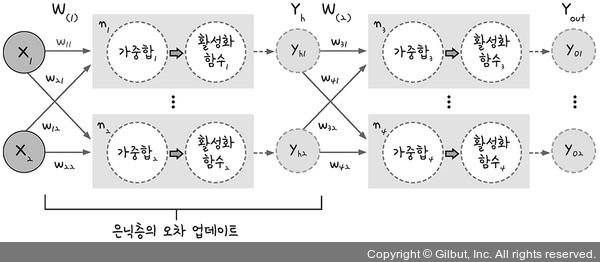
이 두 단계를 각 노드 내부에 표시하고 각 가중치(w) 값과 은닉층의 출력 값(Yh)를 포함하여 표현하면 다음 그림과 같습니다.
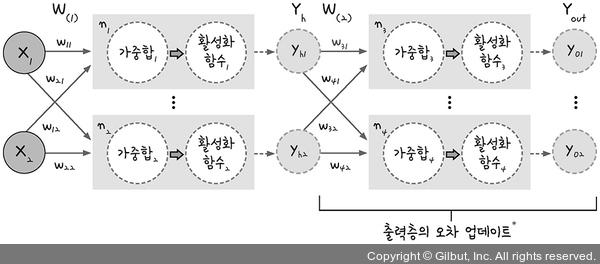
오차 역전파는 Yout 값에서 거꾸로 거슬러 올라가며 가중치 W(2)와 가중치 W(1)이 더는 업데이트되지 않을 때까지 반복하여 계산하는 것입니다.
먼저 W(2)의 값 중 하나인 w31을 업데이트하는 과정을 알아보겠습니다. 오차 역전파의 공식을 이용해 w31을 업데이트하려면 다음 공식으로 계산해야 합니다.

w31 값은 이미 알고 있으므로 여기서 t는 한 단계 앞, t + 1은 현재 단계의 계산을 의미합니다. w31t는 한 단계 앞에서 이미 계산된 값을 의미하므로 여기서는 구할 필요가 없습니다. 따라서 우리가 실제로 구해야 하는 값은 입니다. 이는 오차 Yout를 구하고 이를 w31에 대하여 편미분하라는 뜻입니다. 먼저 오차 Yout를 구해보겠습니다.
2. 오차 공식
오차 Yout 안에는 두 개(yo1, yo2)의 출력 값이 있습니다. 즉, 오차 Yout = 오차 yo1 + 오차 yo2입니다. 여기서 오차 yo1과 오차 yo2는 각각 앞서 배운 평균 제곱 오차를 이용해 구합니다. yo1, yo2의 실제 값을 yt1, yt2이라고 할 때, 다음과 같이 계산합니다.

우리가 해야 할 일은 결국 계산을 통해 나오는 ‘출력 값’이 실제 세상을 통해 알아낸 ‘실제의 값’과 같아지도록 가중치를 조절해 주는 것이지요. 실제 값은 우리의 목표(target)이므로 Ytarget, yt1, yt2라고 표현한 것입니다. yt1, yt2에서의 t는 target, 즉 우리가 구해야 할 목표를 의미합니다.
이제 오차Yout은 다음과 같이 구할 수 있습니다.

3. 체인 룰
이제 이 값을 w31에 대해 편미분해보겠습니다. 의 계산은 합성 함수 미분 공식을 따릅니다. 즉, 체인 룰(chain rule)에 의해 다음과 같이 계산할 수 있습니다.

체인 룰은 연쇄 법칙이라고도 부르며, ‘합성 함수’를 미분할 때의 계산 공식입니다. 여기서 합성 함수란 함수 안에 또 다른 함수가 들어있는 것을 말합니다. f(x) 함수에 들어 있는 x 값이 또 다른 함수 g(x)의 결과일 때를 말하지요.
합성 함수는 f(g(x))와 같이 표시합니다. 그리고 이를 미분하면 안에 있는 g(x)를 x로 대체하여 계산한 값과 g(x)를 미분한 값을 서로 곱해 주면 됩니다. 식으로 표현하면 다음과 같습니다.



4. 체인 룰 계산하기
yo1 - yt1로 편미분되는 과정을 유도하면 다음과 같습니다.

정리하면

이 부분을 보기 앞서 다음 그림을 한 번 더 보겠습니다.
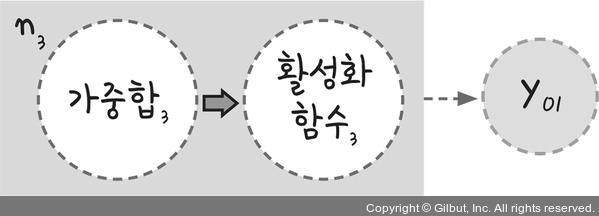
여기서 가중합3이 yo1으로 바뀌는 과정에는 활성화 함수3을 거치는 것을 알 수 있습니다. 가중합3이 활성화 함수3을 통해 yo1이 됩니다. 그러면 가중합3을 yo1에 대해 미분하라는 것은 yo1을 배출한 활성화 함수3을 미분하라는 뜻이 됩니다.

활성화 함수에는 여러 가지가 있지만, 그중에서 시그모이드 함수를 사용했습니다.
함수 σ(x)를 시그모이드 함수

로 정의할 때 이를 미분한
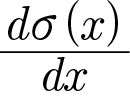
의 값은 다음과 같습니다.

시그모이드 함수 미분 과정

이제 주어진 식을 정리하면

다음과 같습니다.
여기서 가중합3은 n1, n2 노드로부터 전달된 yh 값과 w(2) 값을 통해 만들어집니다.

이를 w31에 대해 편미분하므로 w31과 관계없는 w41yh2과 바이어스 항은 모두 상수로 처리되어 사라집니다. 따라서 남은 w31yh1 항을 미분하면 다음과 같이 정리됩니다.

5. 가중치 업데이트하기
앞서 구한 값을 w31에서 빼주면 새로운 w31 값을 구할 수 있습니다. 따라서 출력층의 가중치를 업데이트하는 방법을 다음과 같이 정리할 수 있습니다.

이 형태는 다음 오차 업데이트 때도 반복해서 나타납니다. 따라서 이 식을 한 번 구해 놓으면 이후는 그대로 사용해서 오차를 구할 수 있습니다. 이를 node3의 델타(delta) 식이라고 합니다.
이 델타 식을 δy라고 하면 우리가 해내야 하는 오차의 업데이트는 다음과 같은 식으로도 구할 수 있습니다.

6. 은닉층의 오차 업데이트
이제 출력층을 거쳐 은닉층의 오차가 업데이트되는 과정을 살펴보겠습니다. 마찬가지로 은닉층의 오차 W(1) 중 하나인 w11의 값을 업데이트하는 방법을 설명하겠습니다.
마찬가지로 가중치에 기울기를 뺀 값을 구해야 합니다. 이때 우리가 구하려는 값이 w11이므로 다음과 같이 계산합니다.

Yh가 은닉층 안에 위치해 있으므로 겉으로 드러나지 않기 때문입니다. 따라서 그 값을 알 수 없습니다. 우리가 알 수 있는 출력 값은 Yout뿐이므로 은닉층의 오차 업데이트를 위한 기울기를 구할 때도 Yout에서 출발해야 합니다.
체인 룰을 적용하여 다음과 같이 계산합니다.
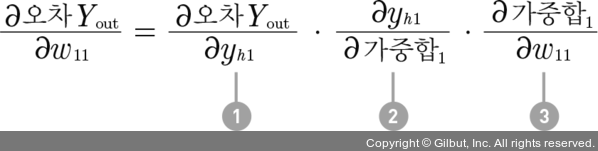
여기서 ➋항과 ➌항은 이전과 같은 방법으로 계산됩니다. 따라서 다음과 같이 바꿔줄 수 있습니다.

7. 은닉층의 오차 계산 방법
이번에는 yh1에 대해 미분해야 합니다. yh1은 오차 yo1과 오차 yo2 의 형성에 모두 관계가 있습니다.
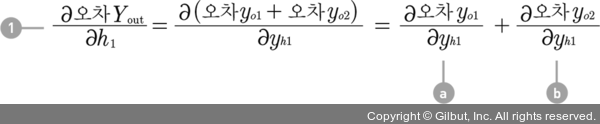
먼저 (a) 부분을 보겠습니다. 체인 룰에 의해 다음과 같이 바뀝니다.

a-1) 과정을 다시 미분하면

으로 바뀌고 이중 먼저

에 포함된 오차 yo1은
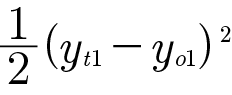
이므로 yo1로 편미분하면 yo1 - yt1이 됩니다.
그리고
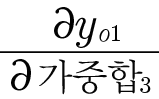
는 앞에서 설명했듯이 시그모이드 함수의 미분이 됩니다. 따라서 yo1 * (1 - yo1)로 계산됩니다.
이제 나머지 a-2를 미분하면 w31이 남습니다.
따라서 앞의 이 식

을 정리하면 아래의 식이 나옵니다.

그런데 여기서 (yo1- yo t) * yo1(1-yo1) 부분이 앞에 나왔던 델타 식(δy)의 형식입니다. 지금 우리는 yo1을 구해야 하므로 델타 식을 δyo1라고 할 때, 위 값은 다음과 같이 간단하게 표시할 수도 있습니다.

이제 다시 돌아가서
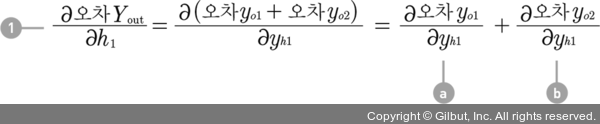
b를 보겠습니다. b부분은 체인 룰에 의해 다음과 같이 변형됩니다.

이중

부분은 체인룰에 의해

다음과 같이 바뀌고
a 식의 풀이에서 설명한 방식과 똑같이 적용되므로 답은

입니다.
여기서 (yo2 - yt2) * yo2(1 - yo2) 부분은 델타 식 형식입니다. 이 델타 식을 δyo2라고 할 때 주어진 식은 다음과 같이 표시할 수 있습니다.

결론적으로 식을 정리하면

이와 같습니다.
델타 식
위의 과정을 통해 output layer와 hidden layer의 업데이트를 위해 도출된 두 개의 식을 보겠습니다.
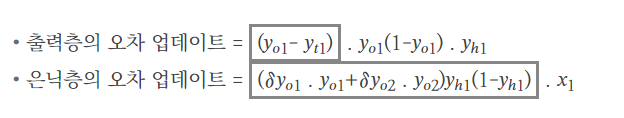
(yo1- yt1)가 (δyo1 yo1+ δyo2 yo2 )로 바뀌었지만, 나머지 부분은 out(1 - out)의 형태를 띠고 있습니다.
여기서 (yo1- yt1)는 오차의 값입니다. 하지만 은닉층에서는 이렇게 오차를 계산할 수 없습니다. 은닉층에서 일어나는 일은 우리 눈으로 볼 때는 알 수 없으므로 출력층에서 yo 값을 가져와서 계산해야 합니다. 그러므로 위 식의 (δyo1 . yo1+ δyo2 . yo2)처럼 형태가 복잡해졌을 뿐 결국 오차를 나타냅니다.
따라서 두 식 모두 ‘오차 . out(1 - out)’의 형태, 즉 델타 식의 형태로 단순화할 수 있었습니다.
델타 식이 중요한 이유는 이렇게 한 층을 거슬러 올라갈 때마다 같은 형태가 계속 나타나기 때문입니다.
은닉층의 델타 식이므로 이것을 δh라고 할 때, 은닉층의 가중치 업데이트를 식으로 표현하면 다음과 같습니다.


궁금했던 부분인데 좋은 글 감사합니다. 많은 도움 되었습니다. ^^