개념 내용, 이미지 출처: 딥러닝 교과서
이번 글은 오차 역전파 알고리즘(backpropagation algorithm)에 대해 공부하고 정리해보도록 하겠습니다.
신경망에서 경사 하강법을 적용할 때 손실 함수에서 각 가중치까지 신경망의 역방향으로 실행했던 함수를 따라가며 미분을 계산해서 곱했습니다. 만일 이 과정을 모든 파라미터에 대해 개별적으로 진행한다면 같은 미분을 여러 번 반복하는 비효율적인 계산 과정을 거치게 되는데요. 이런 문제를 해결하기 위해 제안된 방법이 오차 역전파 알고리즘(backpropagation algorithm)입니다.
1. 역전파 알고리즘
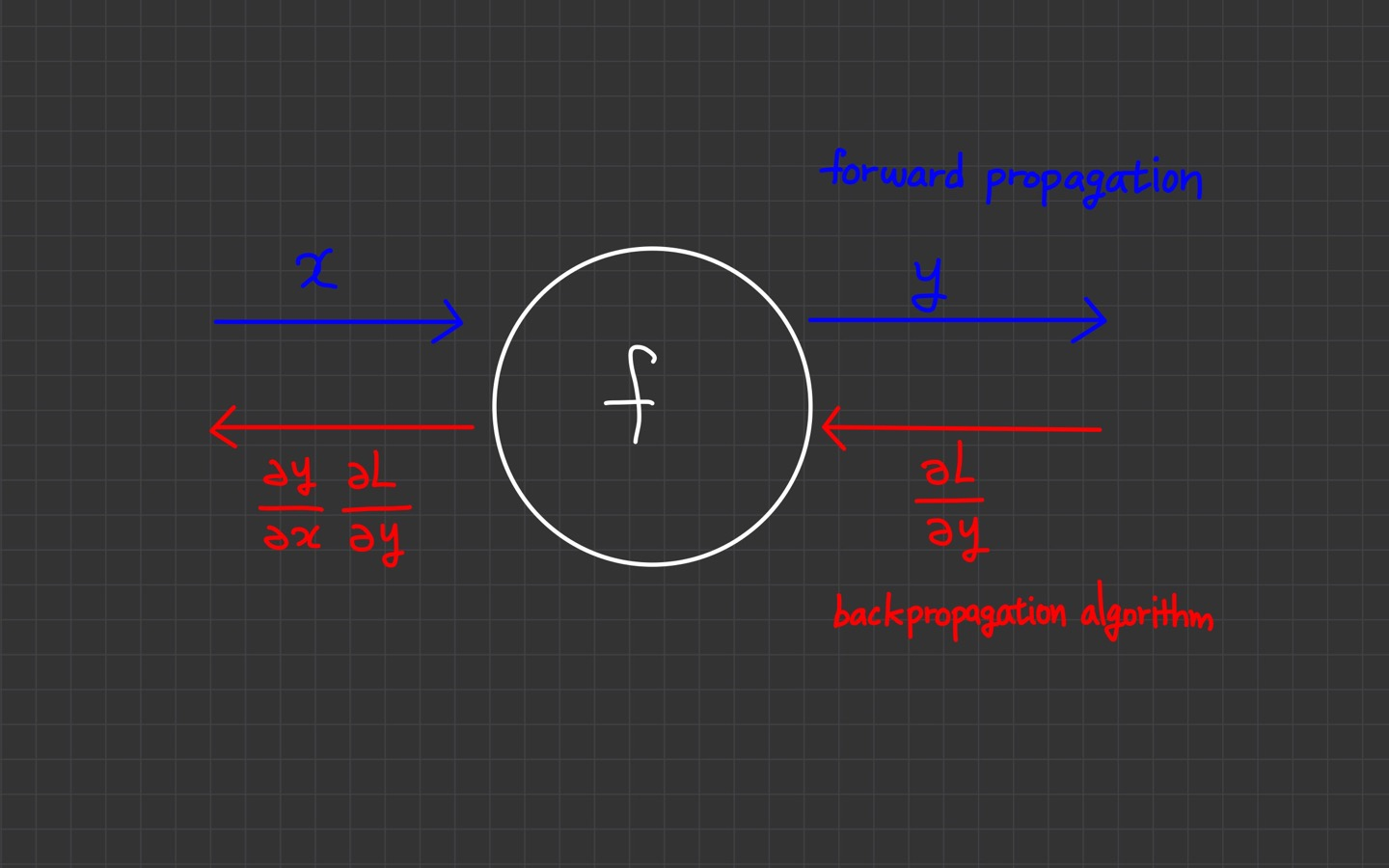
계산 과정을 그래프로 나타냈습니다.
왼쪽에서 오른쪽으로 진행하는 단계를 순전파(forward propagation)라고 합니다. 입력값 는 함수 를 거쳐 로 순전파되고 있습니다.
반대로 오른쪽에서 왼쪽으로 진행하는 단계를 역전파(backpropagation)이라고 합니다. 빨간색 화살표가 역전파를 의미합니다.
여기서는 하나의 노드만 존재하지만 실제 neural network는 노드가 많은 계산 그래프입니다. 네트워크는 최종적으로 정답과 비교한 다음에 loss를 구합니다.
목적은 neural network의 오차를 줄이는 것이기 때문에 각 parameter별로 loss에 대한 gradient를 구한 뒤 gradient가 향한 쪽으로 parameter들을 업데이트합니다.
입력값 에 대한 loss의 변화량, 를 구할 차례입니다. 이는 미분의 연쇄법칙(chain rule)*에 의해 계산할 수 있습니다.
는 Loss로부터 흘러들어온 gradient입니다. 는 현재 입력값에 대한 현재 연산결과의 변화량, 즉 local gradient입니다.
현재 입력값 에 대한 loss의 변화량은 loss로부터 흘러들어온 gradient에 local gradient를 곱해서 구해야 합니다.
이 gradient는 다시 앞쪽에 배치돼 있는 노드로 역전파됩니다.
뉴런 의 또 다른 가중치 에 대해 미분한다고 가정하면,
연쇄 법칙(chain rule)으로 미분을 표현해보면 마지막 항인 를 제외한 앞부분의 공통부분이 의 미분과 동일하다는 것을 알 수 있습니다.

따라서 공통부분은 한 번 계산해두면 같은 뉴런에 속한 모든 가중치의 미분을 계산할 때 재사용할 수 있습니다.

공통부분의 계산을 중복하지 않기 위해,
손실 함수에서 시작해서 입력 계층 방향으로 계산된 미분값을 역방향으로 전파해주면 됩니다.
이때 각 뉴런의 공통부분에 해당하는 미분값을 오차라고 하며, 오차를 역방향으로 전파하며 미분을 계산한다고 하여
이 방법을 오차의 *역전파 알고리즘이라고 부릅니다.
2. 역전파 알고리즘의 실행 순서
역전파 알고리즘에서 손실 함수부터 시작해 가중치 에 도달할 때까지의 미분 순서를 알아보겠습니다.
1) 손실 함수 미분
역전파 알고리즘에서 손실 함수부터 시작하므로, 먼저 손실 함수에 대한 입력의 미분을 계산해서 출력 계층에 전달합니다.
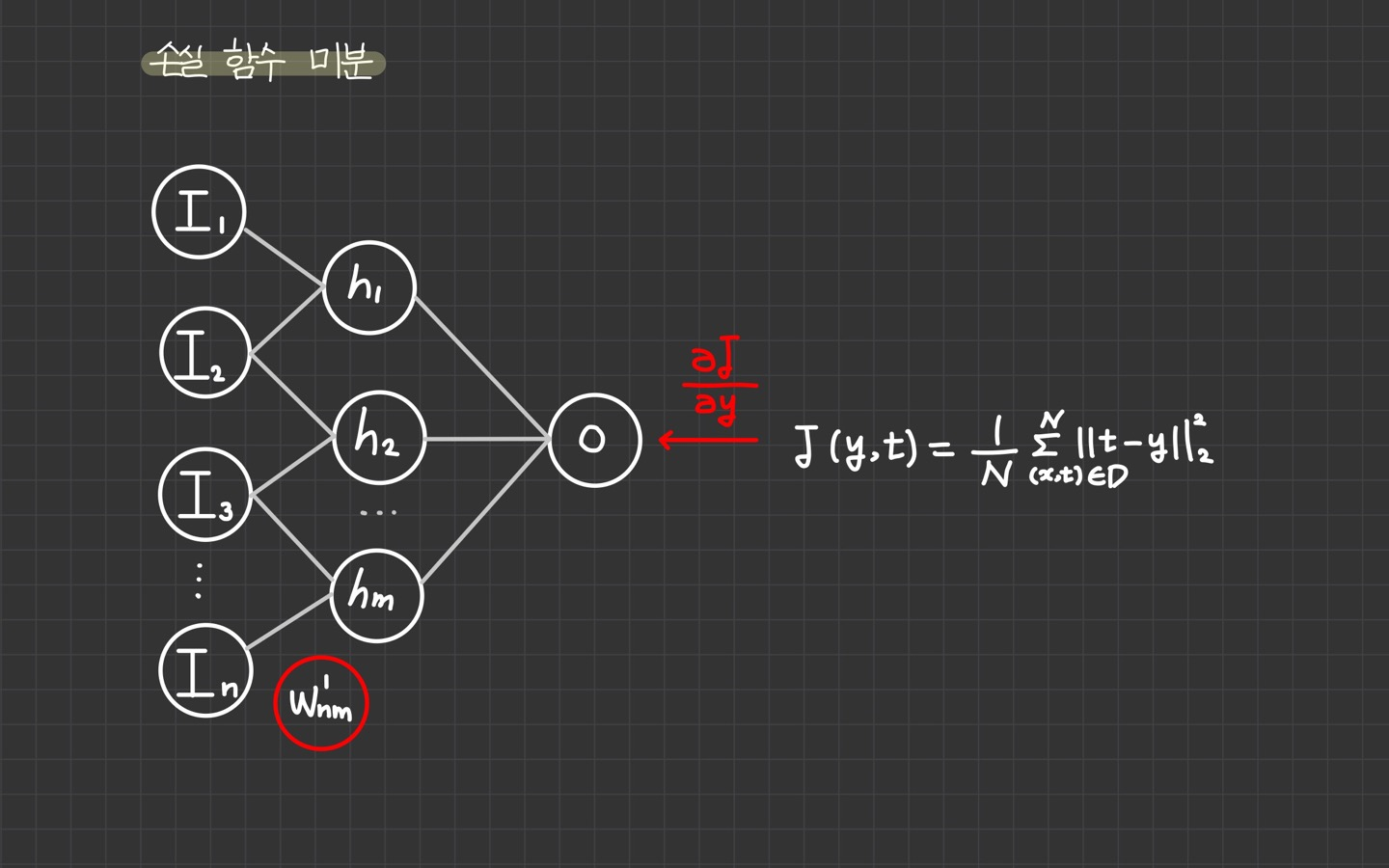
1️⃣ 손실함수 미분
-
손실 함수 지역 미분: 손실 함수 의 지역 미분 를 계산한다.
-
손실 함수 전역 미분: 손실 함수 전역 미분은 지역 미분 과 같다.
2️⃣ 출력 뉴런에 미분 전달
- 손실 함수 전역 미분 를 출력 계층 에 전달한다.
2) 출력 뉴런 미분
출력 뉴런 는 전역 미분 를 전달받고 가중치의 미분을 계산해서 가중치를 업데이트하고,
입력의 미분을 계산해서 은닉 계층에 전달합니다.
는 활성 함수 와 가중합산 으로 이루어지므로 미분을 별도로 수행해야 합니다.
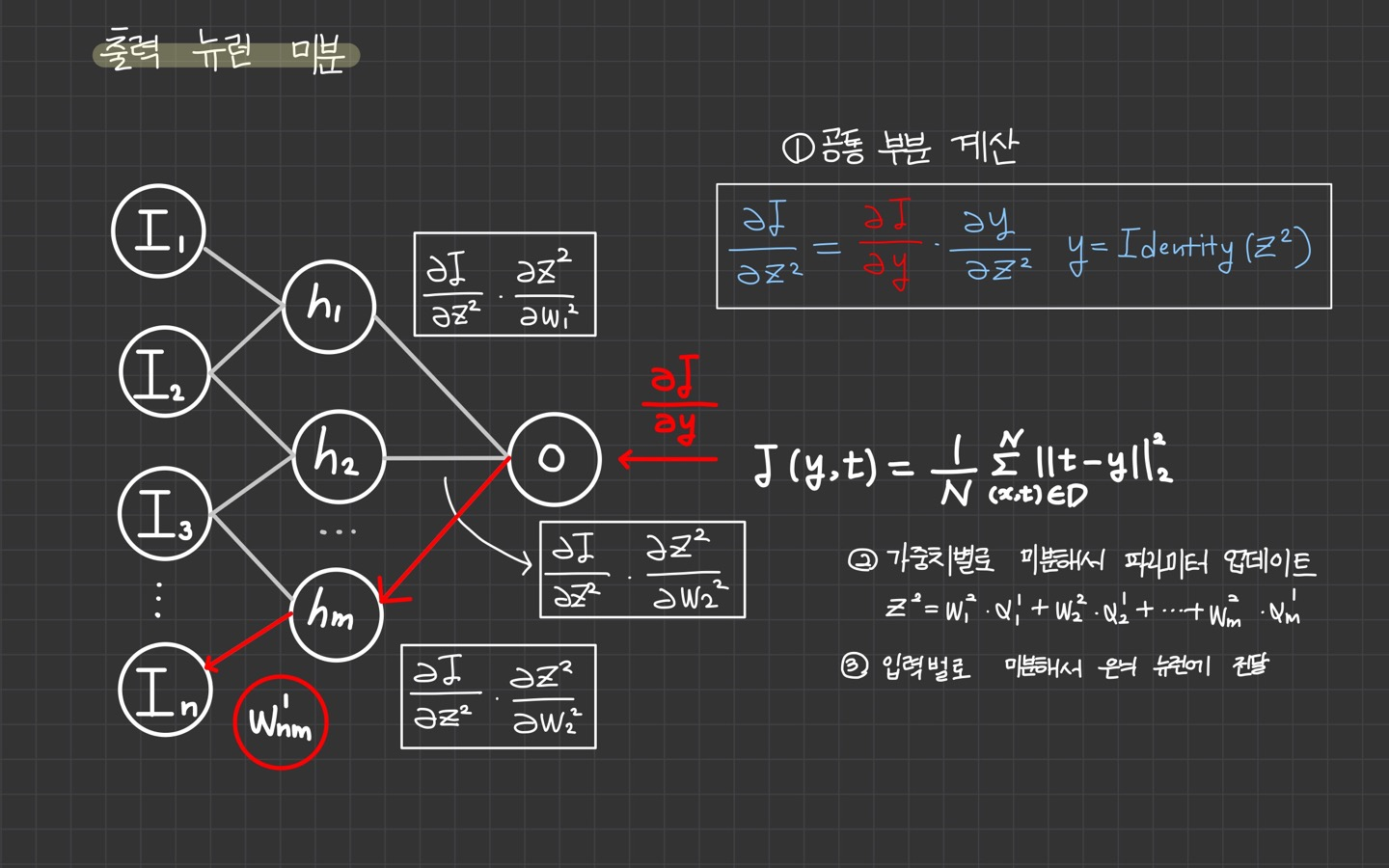
1️⃣ 공통 부분 계산
-
활성 함수 지역 미분: 활성 함수 의 지역 미분 를 계산한다.
-
활성 함수 전역 미분: 와 를 곱해서 활성 함수 전역 미분을 계산한다.
-
공통 부분 계산: 활성 함수의 전역 미분 이 뉴런의 공통부분이 된다.
2️⃣ 가중치 업데이트
-
가중치 지역 미분: 가중 합산식 에 대해 가중치별로 지역 미분 , , ..., 을 계산한다.
-
가중치 전역 미분: 공통 부분 와 , , ..., 을 곱해서 가중치의 전역 미분 , , ..., 를 계산한다.
-
가중치 업데이트: , , ..., 를 업데이트한다.
3️⃣ 은닉 계층에 미분 전달
-
입력 지역 미분: 가중 합산식 에 대해 입력별로 지역 미분 , , ..., 을 계산한다.
-
입력 전역 미분: 공통 부분 과 , , ..., 을 곱해서 입력의 전역 미분 , , ..., 을 계산한다.
-
은닉 뉴런에 미분 전달: 은닉 뉴런 에 입력의 전역 미분 , , ..., 을 전달한다.
3) 은닉 뉴런 미분
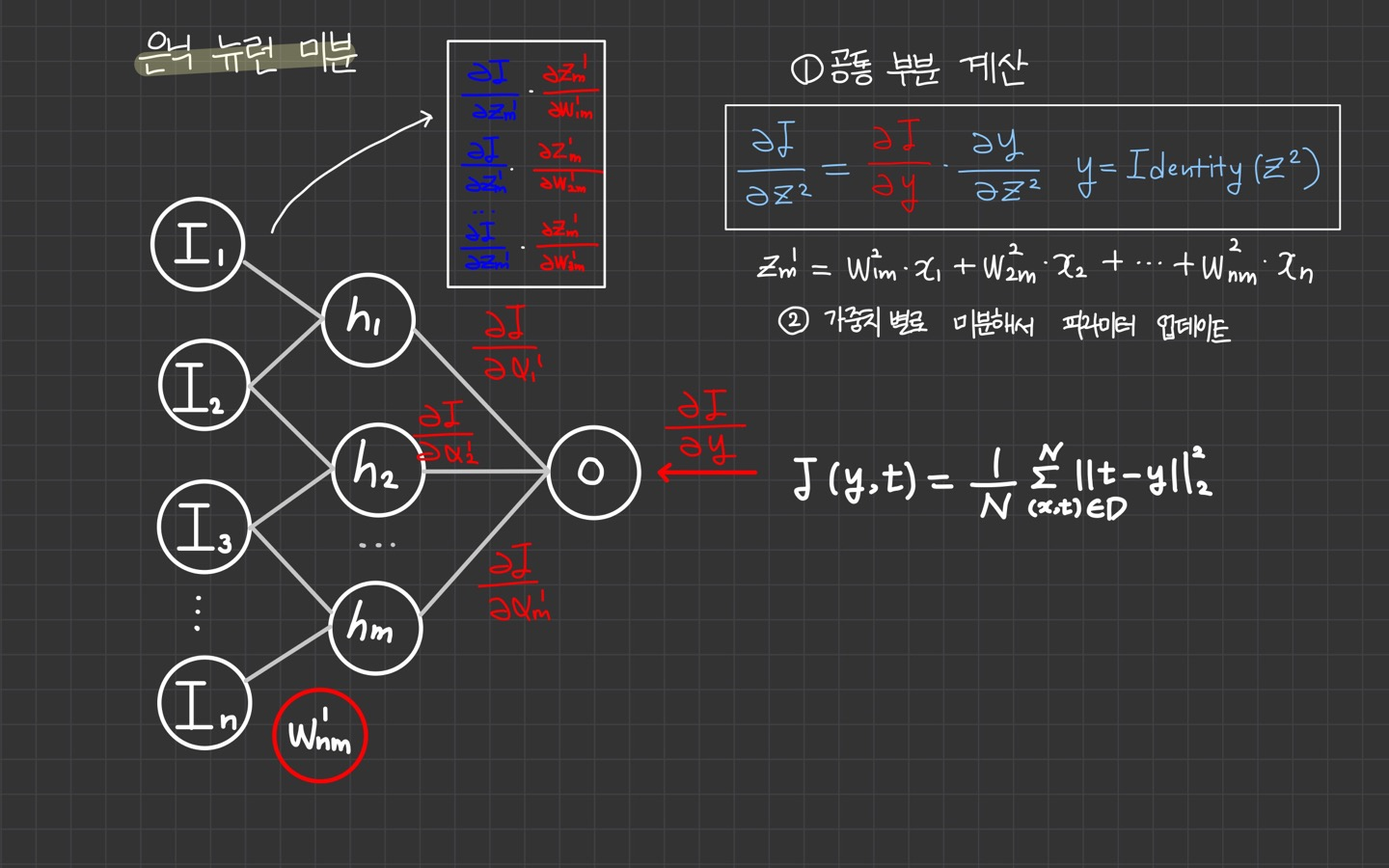
1️⃣ 공통 부분 계산
-
활성 함수 지역 미분: 활성 함수 의 지역 미분 을 계산한다.
-
활성 함수 전역 미분: 과 을 곱해서 활성 함수 전역 미분 을 계산한다.
-
공통부분 계산: 활성 함수의 전역 미분이 뉴런의 공통 부분이 된다.
2️⃣ 가중치 업데이트
-
가중치 전역 미분: 가중 합산 식 에 대해 가중치별로 지역 미분 , , ..., 을 계산한다.
-
가중치 전역 미분: 공통 부분 과 , , ..., 을 곱해서 가중치의 전역 미분 , , ..., 를 계산한다
-
가중치 업데이트: , , ..., 으로 가중치 을 업데이트한다.
3️⃣ 입력 계층에 미분 전달
- 입력 계층에는 가중치가 없으므로 미분을 전달하지 않아도 된다.
4) 역전파 알고리즘 종료
다른 은닉 뉴런에 대해서도 같은 방식으로 가중치를 업데이트합니다.
은닉 계층의 가중치 업데이트가 완료되면 역전파 알고리즘도 종료합니다.
3. 뉴런 관점에서 보는 역전파 알고리즘
역전파 알고리즘을 하나의 뉴런 관점에서 보면 미분 계산 규칙을 좀 더 쉽게 이해할 수 있습니다.
아래 그림과 같이 입력 x, y가 있고 활성함수 를 실행하는 뉴런이 있다고 하면, 뉴런 출력 z는 손실 함수의 입력입니다.
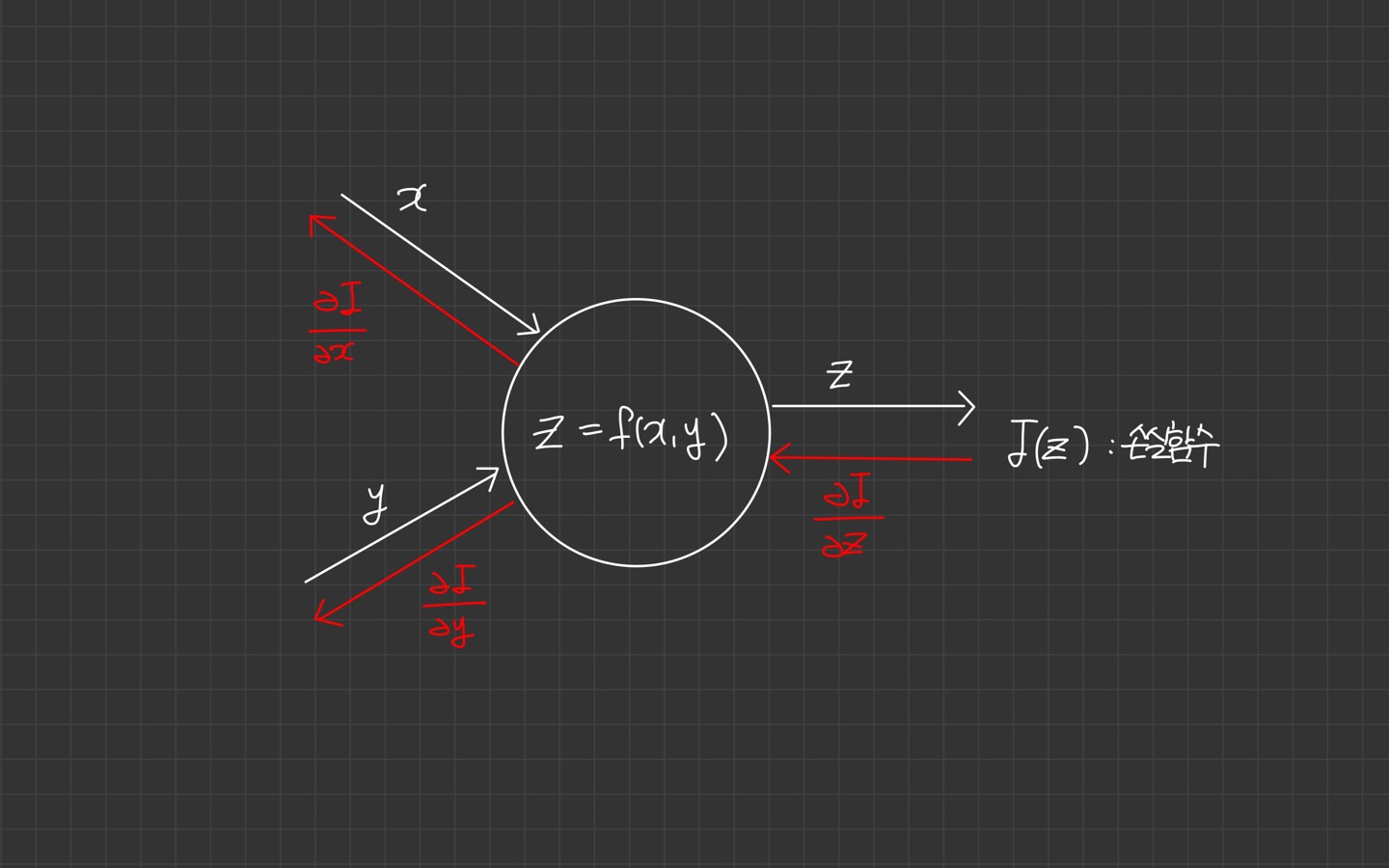
역전파 알고리즘을 적용해봅시다.
손실함수 를 에 대해 미분해서 를 구하고 뉴런에 미분값을 전달합니다.
뉴런의 지역 미분을 구하고, 함수 를 에 대해 미분해서 와 를 구합니다.

위의 과정을 그림으로 나타낸 것이 아래의 이미지이다.
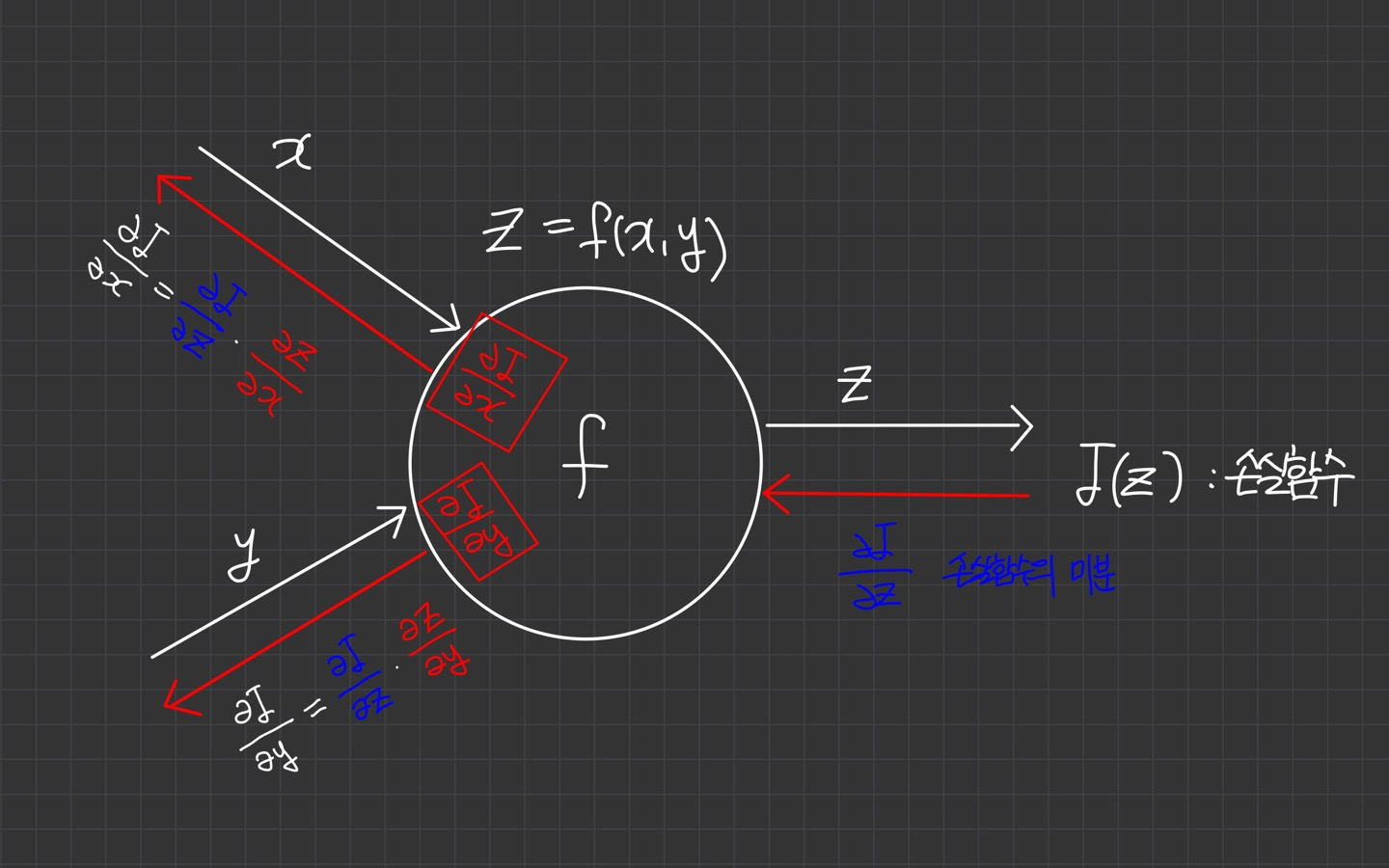
이렇게 하나의 뉴런 입장에서 미분을 계산하는 방식은 지역 미분을 구해 전달받은 전역 미분에 곱하는 것이 전부입니다.
뉴런의 가중치를 업데이트 하기 위해
- 가중치에 대한 지역 미분을 구한다
2.전달 받은 전역 미분에 곱해서 가중치의 전역 미분을 계산한다.
- 계산된 가중치의 전역 미분으로 가중치를 업데이트 한다.
은닉 계층에 미분을 전달하기 위해
-
입력에 대한 지역 미분을 구한다.
-
전달받은 전역 미분에 곱해서 입력에 대한 전역 미분을 계산한다.
-
계산된 입력에 대한 전역 미분을 다음 은닉 뉴런에 전달한다.
이렇게 여기까지 뉴런 관점에서 보는 역전파 알고리즘을 살펴보았다.
4. 계층 단위의 미분
미분 과정은 계층 단위로도 동일한 방식으로 진행할 수 있습니다.
실제 구현 시 계층 단위로 계산하는데 달라지는 점은 뉴런에서 벡터로 표현했던 가중치가 계층에서는 행렬로 표현된다는 점입니다.
따라서 뉴런에서 가중치의 미분을 나타내는 gradient는 벡터로 표현되지만, 계층에서 가중치와 미분을 나타내는 야코비안(jacobian)은 행렬로 표현됩니다.
역전파 알고리즘은 신경망과 같은 그래프 구조에서 연쇄 법칙을 이용해 미분을 효과적으로 수행하기 위한 알고리즘입니다.
따라서 신경망 학습은 역전파 알고리즘을 이용해서 미분을 계산하고, 경사 하강법과 같은 최적화 알고리즘을 통해 파라미터를 업데이트하면서 최적해를 찾는 최적화 과정으로 볼 수 있습니다.
5. 주요 활성 함수의 미분
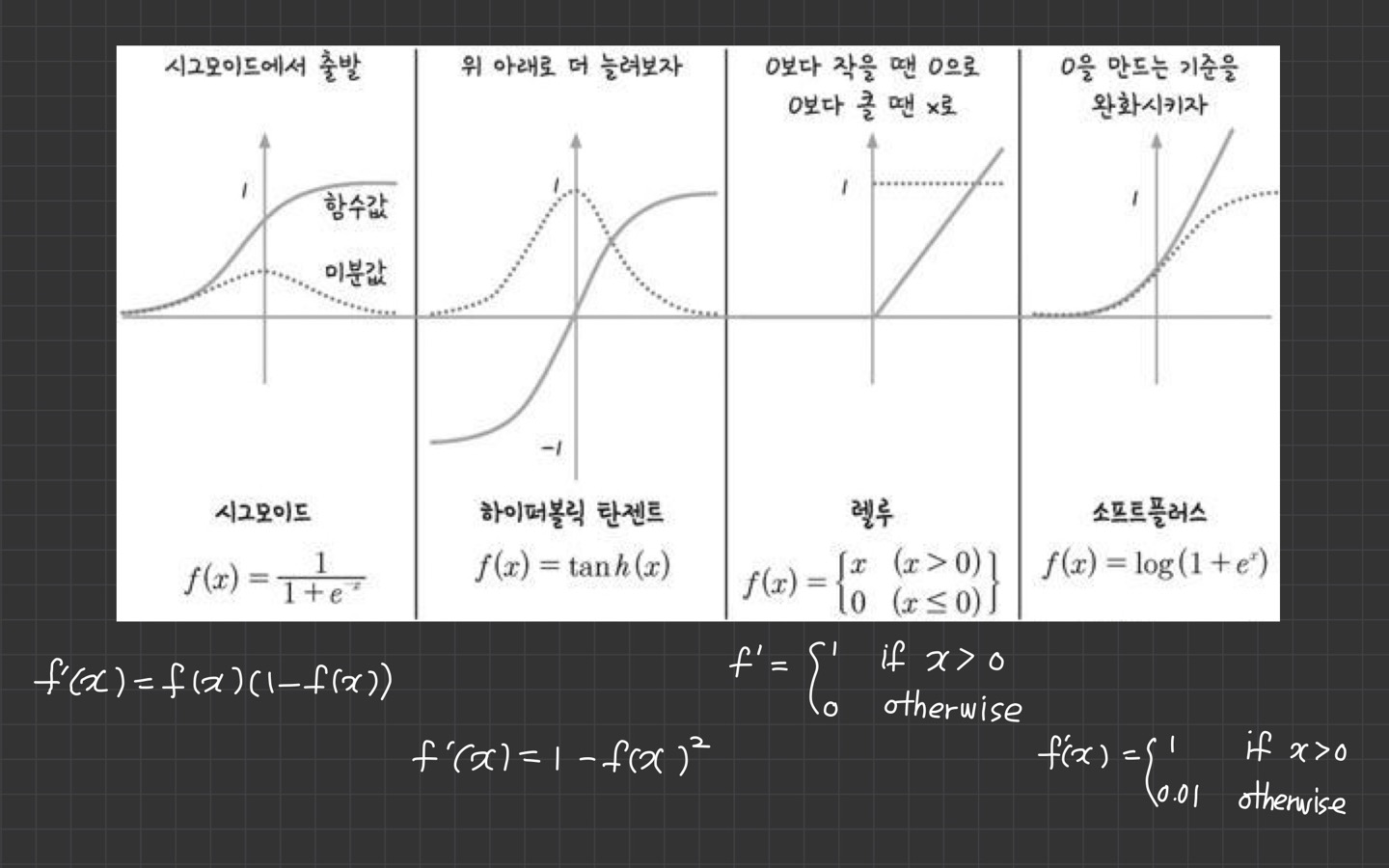
활성 함수의 미분은 간단한 형태로 정으되는데요. 시그모이드 계열의 도함수는 활성 함수 의 식으로 정의되어 계산이 간단합니다.
ReLU 계열은 구간 선형 함수이므로 미분값이 상수입니다. 그래서 미분이 별도로 필요하지 않습니다.
Reference
📗 개념 내용 및 이미지 출처: 딥러닝 교과서
📒 오차 역전파 (backpropagation)

대구캠 1기입니다. 검색하다 나왔는데 양재 퍼실님이네요 팔로우?하겠습니다 자주 참조 하겠습니다ㅎ