개념 내용, 이미지 출처: 딥러닝 교과서
신경망의 학습 목표
신경망 최적화 알고리즘은 대부분 경사 하강법에서 확장된 형태입니다! 신경망의 기본 알고리즘으로 경사하강법을 채택한 이유와 최적화 원리를 살펴보도록 하겠습니다.
신경망의 손실 함수는 차원이 매우 높고 복잡한 모양을 갖고 있습니다.
손실 함수에는
- global minimum
- local minimum
이 있습니다.
global minimum은 함수 전체에서 가장 낮은 곳을 말하며 최솟값이라고 합니다.
local minimum은 함수에서 부분적으로 낮은 곳을 말하며 극소값이라고 합니다.
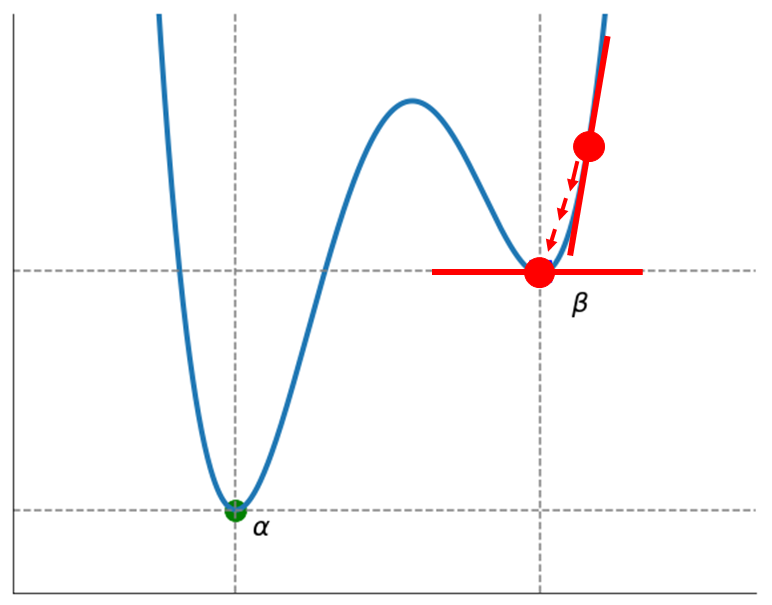
위 그림을 예시로 들면, 가 global minimum이라 볼 수 있고, 가 local minimum이라 볼 수 있습니다.
하지만 2차원 그래프처럼 단순화한다면 찾기 쉽지만 문제가 크고 복잡할 경우 global minimum을 찾기가 어렵고 불가능 할 수 있습니다.
따라서 대부분의 알고리즘은 local minimum을 찾는 것이 목표이고, 여러 개를 찾아 가장 좋은 해를 선택하는 방식을 고려하기도 합니다.
최적화 알고리즘
1차 미분
- 경사 하강법
- 경사 하강법의 변형 알고리즘: SGD, SGD Momentum, AdaGrad, RMSProp, Adam
1.5차 미분
- 준 뉴턴 방법
- 켤레 경사 하강법
- 레벤버그 마쿼트 방법
2차 미분
- 뉴턴 방법
- 내부점법
2차 미분 방식은 curvature을 사용하므로 최적해를 빠르게 찾을 수 있지만, 손실 함수 곡면이 볼록해야만 최적해를 찾을 수 있습니다. 그래서 계산 비용과 메모리 사용량이 많아 신경망에서는 사용하기 어렵습니다.
1.5차 미분 방식은 1차 미분을 이용해 2차 미분을 근사하는 방식인데, 신경망 학습과 별도로 2차 미분을 근사하는 알고리즘을 실행해야하고 2차 미분값도 저장해야 하므로 메모리 사용량이 많습니다.
1차 미분은 상대적으로 수렴 속도는 느리지만, 손실 함수 곡면이 볼록하지 않아도 최적해를 찾을 수 있어서 손실 함수 곡면이 매우 복잡한 신경망에서도 안정적으로 사용이 가능합니다.
그래서 주로 1차 미분 방식인 경사 하강법과 이를 개선한 알고리즘을 사용합니다.
경사 하강법(Gradient Descent)
경사 하강법은 손실 함수의 최소 지점을 찾기 위해 경사가 가장 가파른 곳을 찾아 한 걸음씩 내려 가는 방법이라 볼 수 있습니다.
손실 함수의 기울기를 구하고 기울기의 반대 방향으로 내려 가며 최소 지점을 찾습니다.
이전에 경사하강법에 대해 간단히 포스팅한 적이 있습니다.
해당 내용을 먼저 참고하시면 좋을 것 같습니다. 👉 Gradient Descent - 경사하강법, 편미분, Local Minimum

경사하강법에서는 파라미터 업데이트 과정을 반복하다가 가 임계치 이하가 되면 최소 지점에 도달했다고 판단하고 이동을 멈춥니다.
기울기는 손실함수를 파라미터 에 대해 미분한 그레이디언트를 의미합니다.
그레이디언트란?
그레이디언트란 형태의 실수 함수의 미분을 말합니다.
과 같이 변수 가 차원 벡터이고 함숫값이 실수인 경우, 입력 벡터의 요소별로 함수 f(x)를 편미분한 벡터를 그레이디언트라고 한다.
따라서 그레이디언트는 에서 함수 가 증가하는 방향과 증가율을 나타낸다.
신경망에서 경사 하강법 적용
2계층 신경망 회귀 모델
은닉 계층의 활성 함수는 ReLU, 회귀 모델이므로 출력 계층의 활성 함수는 항등 함수, 손실 함수 는 평균제곱오차입니다.
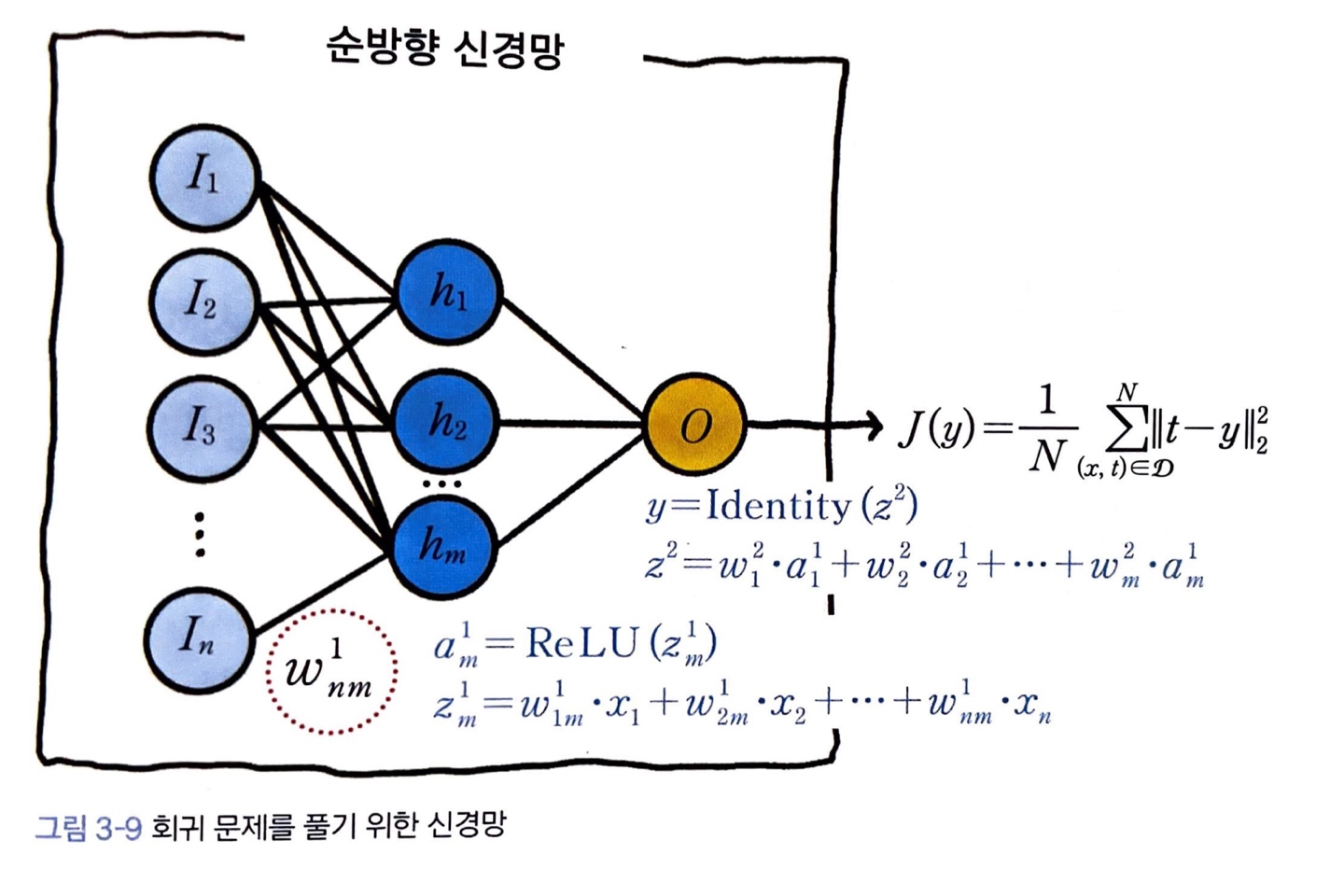
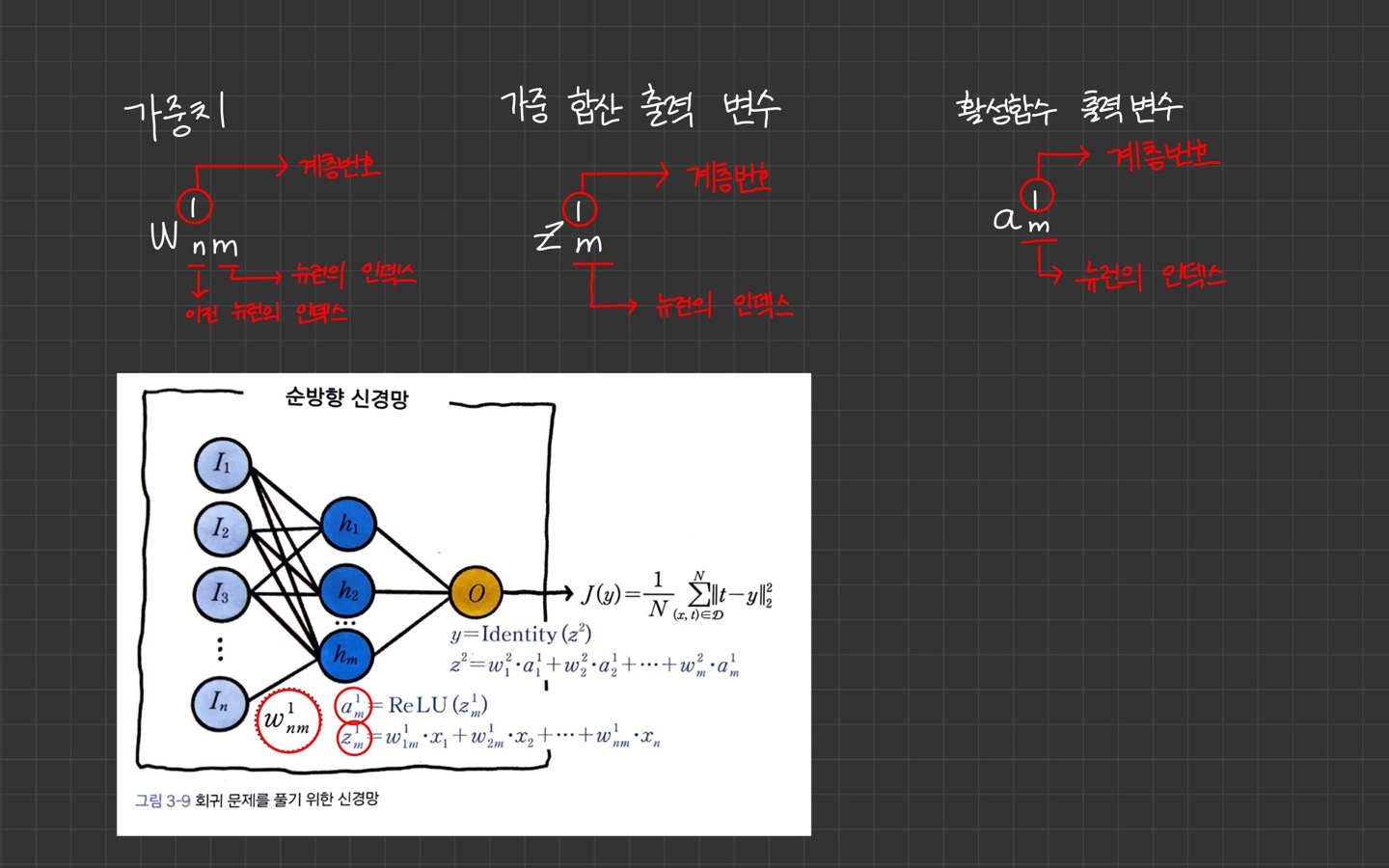
표기 설명은 아래를 참고해주세요.
경사하강법을 이용해서 가중치 값을 업데이트하려면 먼저 손실 함수에 대한 가중치의 미분 을 구해서 다음 업데이트 식으로 을 로 변경합니다.
그런데 이 업데이트 식은 바로 계산할 수가 없습니다.
손실함수에는 가중치 변수 이 포함되지 않아서인데요.
신경망에서 가중치 변수 는 은닉 뉴런에서 정의되며 출력 뉴런을 거쳐서 손실 함수에 간접적으로 영향을 미칩니다.
즉, 손실함수는 합성 함수로 정의되며 합성 함수를 미분하려면 연쇄 법칙(chain rule)을 사용해야 합니다. 연쇄 법칙을 사용해서 표현하면

위 사진의 식과 같습니다.
연쇄 법칙을 사용한 미분 계산
연쇄 법칙으로 합성 함수의 미분을 표현할 때는 합성 함수의 실행 순서에 따라 각 함수의 미분을 곱해줍니다.
가중치 변수 가 정의된 은닉 뉴런부터 손실 함수까지 실행되는 함수의 순서는 아래와 같습니다.

- 식 1의 미분은 가중 합산 을 가중치 변수 로 미분한 값입니다.
- 식 2의 미분은 활성 함수 를 입력 변수 으로 미분한 값입니다.
- 식 3의 미분은 가중 합산 를 입력 변수 로 미분한 값입니다.
- 식 4의 미분은 활성 함수 를 입력 변수 로 미분한 값입니다.
- 식 5의 미분은 손실 함수 를 입력 변수 y로 미분한 값입니다.
각 함수의 미분을 곱하면 연쇄 법칙 형태로 을 정의할 수 있습니다.
신경망에서 연쇄 법칙으로 미분하는 과정
신경망에서 연쇄 법칙으로 미분을 계산하는 과정을 살펴보겠습니다.
손실함수 를 계산한다면 가중치 까지 각 함수를 거꾸로 따라가며 5, 4, 3, 2, 1 의 순으로 미분을 계산해서 곱하면 됩니다.
이 과정을 아래 그림으로 살펴보면 빨간색의 화살표를 따라 신경망의 역방향으로 미분을 계산해서 곱해 나갑니다.
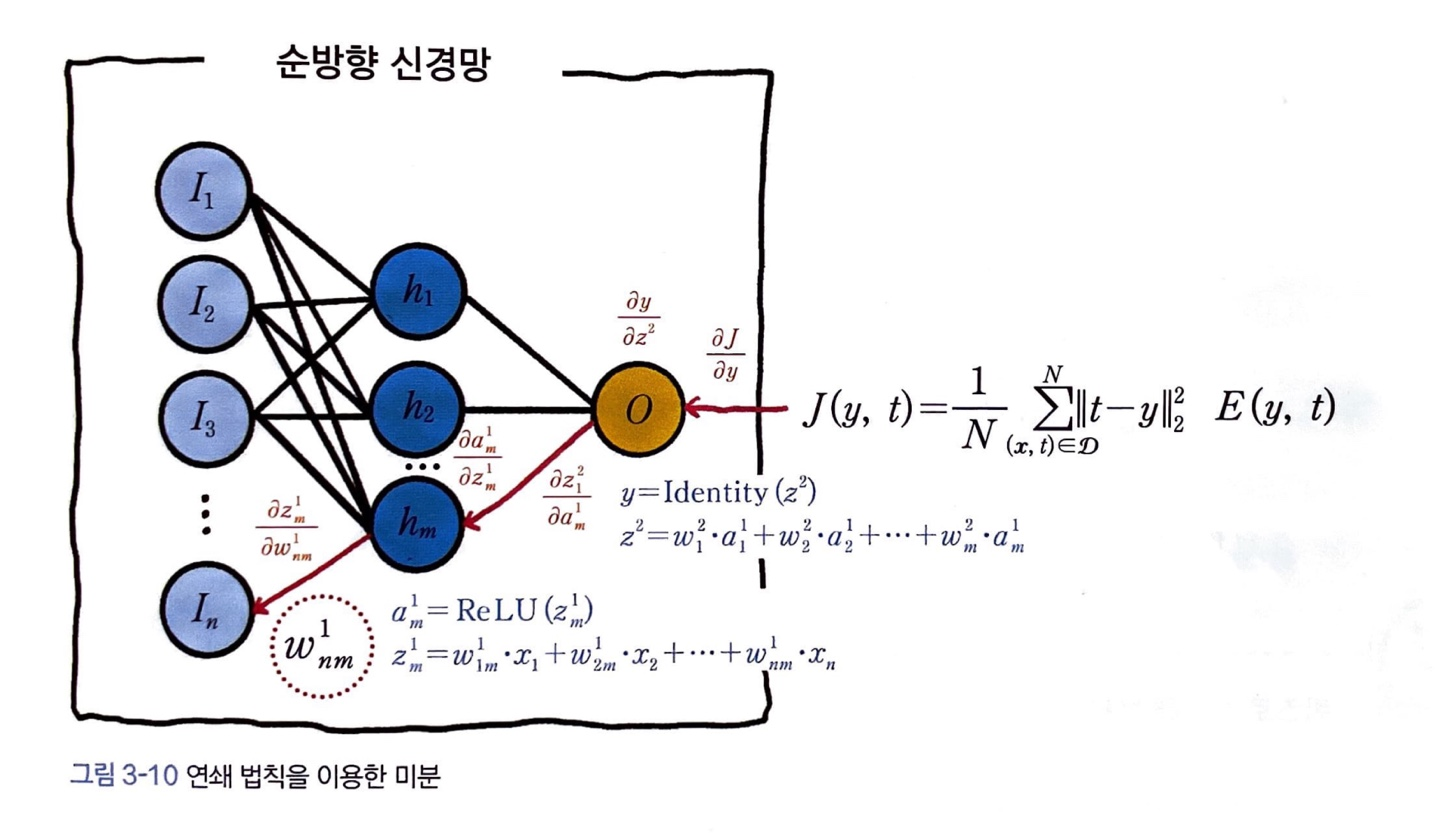

같은 방식으로 신경망의 모든 파라미터에 미분의 연쇄 법칙을 적용하여 경사 하강법을 적용할 수 있습니다!
