이번엔 Batch Normalization의 개념을 정리하려고 합니다. 제가 참고한 포스팅과 영상 등은 아래 Reference에 모두 남겨놓았으니 참고 부탁드립니다.😊
Reference
- 📄 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
- 📄 Normalizing your data (specifically, input and batch normalization)
- 📄 Breaking the ice with Batch Normalization
- 💻 배치 정규화(Batch Normalization) [꼼꼼한 딥러닝 논문 리뷰와 코드 실습]
Contents
- Reference
- Review
- Why normalize?
- Batch Normalization
- Internal Covariate Shift
- Implementaion
- Not use bias
- Summary
Review
Batch Normalization는 neural network를 중점에 두고 데이터 정규화에 대한 고려 사항에 대해 설명합니다.
이 개념을 이해하기 위해선 gradient descent를 이해하는 것이 중요합니다.
간단히 복습하고 넘어가겠습니다.
신경망을 훈련할 때 실제 출력과 예상 출력값을 비교합니다. 그런 다음 gradient descent를 사용하여 출력값을 실제 결과 간의 차이를 최소화하는 방향으로 model의 parameter를 업데이트합니다.
다시 말해, 우리는 model의 예측에서 관찰한 오류를 최소화하려고 시도합니다.
parameter를 업데이트하는 정확한 방법은 초기에 선택한 gradient descent에서 최적화 기술(optimizer) SGD, RMSProp, Adam 등의 변형에 따라 살짝씩 다른 방법이 나왔습니다.
parameter의 update되는 크기를 조절하는 learning rate의 개념도 있었습니다.
이 비율은 parameter가 업데이트하는 과정에서 최적의 값을 피해 급격히 변하는 것을 조절합니다.
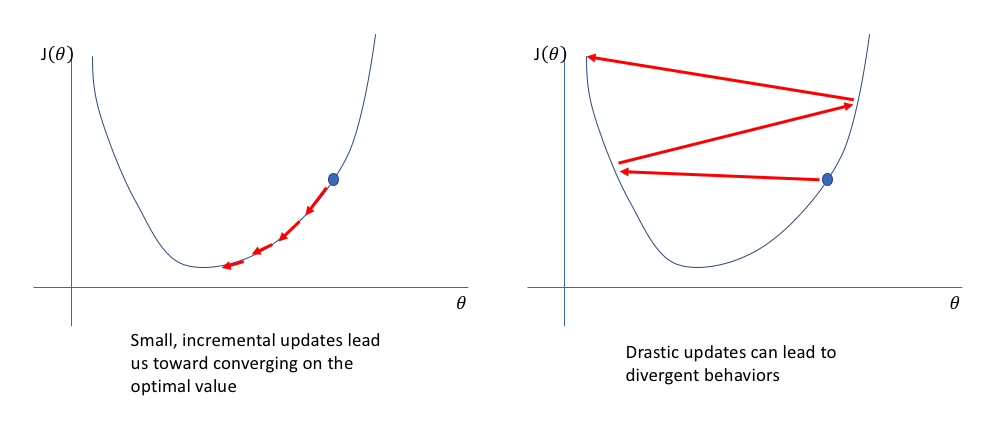
왼쪽은 optimal value를 향해 수렴하기 위해 update되고 있습니다.
오른쪽은 optimal value로 향하지 못하고 발산하고 있습니다.
gradient descent는 loss function이 최소화되도록 각 매개변수에 대한 값을 찾기 위해 loss function의 표면을 탐색합니다.
이 경우 saddle point에 갇히는 것을 방지할 수 있도록 효율적으로 update하는 방법이 아래 그림으로 살펴볼 수 있습니다.
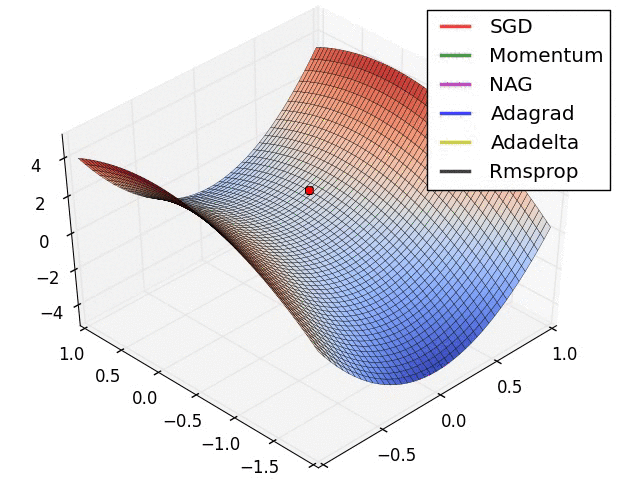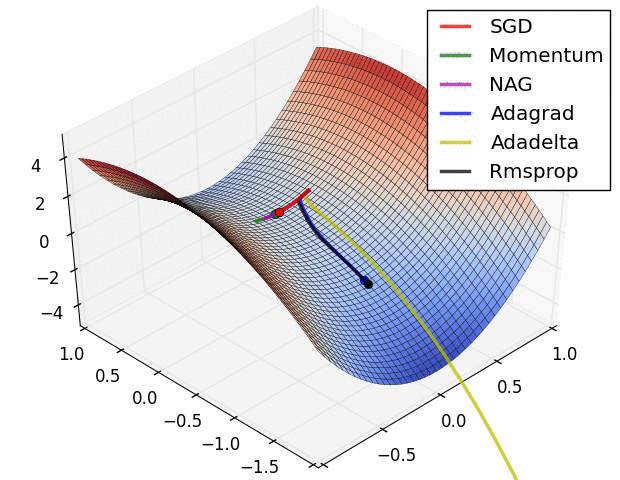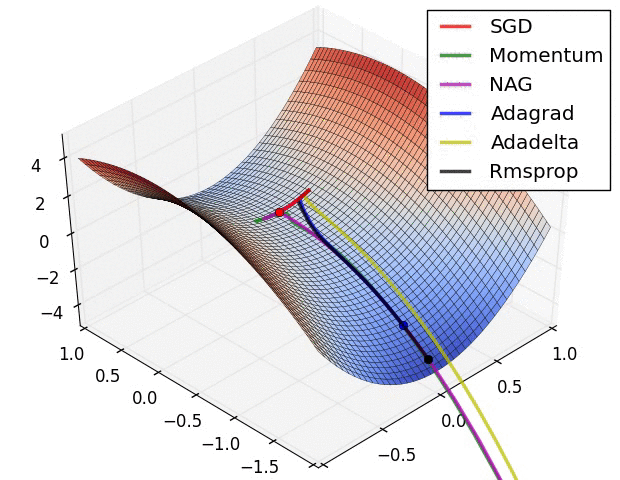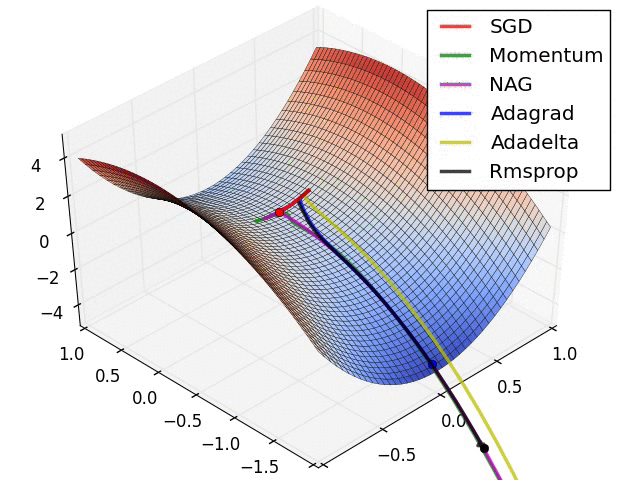
parameter와 loss function의 값을 표현한 3차원 공간
중요한 점은 loss function의 표면이 network의 parameter 값으로 특성화되며 위의 시각화는 parameter 값 범위가 loss function에 미치는 차원을 나타낸다고 볼 수 있습니다.
여기까지 최적의 parameter 값을 찾는 과정을 다시 살펴보았습니다.
슬슬 본론으로 들어가겠습니다.
Why normalize?
그렇다면 정규화되지 않은 데이터의 문제는 무엇일까요?
입력값이 2개인 simple neural network를 떠올려보겠습니다.
(0,1)의 값을 가지는 와 (0, 0.01)의 값을 갖는 의 input data가 있습니다.
network는 일련의 linear combination과 nonlinear activations을 통해 입력 값이 학습되며, 각 입력의 parameter도 다른 척도에 존재합니다.
와 의 feature는 다른 범위에 있기 때문에 학습 가능한 parameter , 가 갖는 값의 범위는 상당히 다르게 됩니다.
특정 parameter gradients에 더 중점을 두는 loss function으로 이어질 수 있습니다.
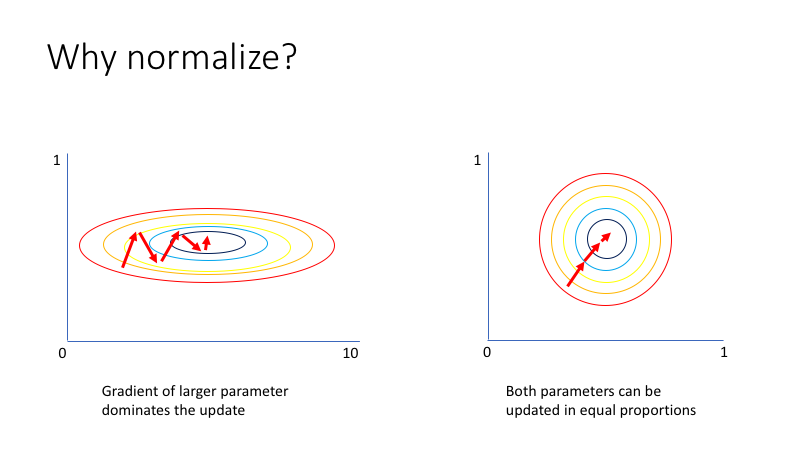
위 그럼으로 살펴보면 unnormalized input features는 왼쪽처럼 길게 나타나고, Normalizing inputs는 더 대칭적인 모양을 갖습니다.
왼쪽 그림의 경우, w가 최적의 값을 찾는데 앞뒤로 많이 진동하는 것을 볼 수 있습니다. 이때는 작은 learning rate를 사용해야하고, 학습 시간이 길어지며 converge하는데까지 오래 걸립니다.
오른쪽 그림의 경우, 데이터가 normalize되면 원 모형의 loss function을 갖게 됩니다. w가 초기화되는 위치는 중요하지 않게 되며, 더 높은 learning rate를 사용할 수 있습니다.
또한, 진동하지 않고 최솟값으로 내려갑니다. 따라서 training time이 더 빠르면서 더 낮은 error값으로 converge합니다.
그래서 모든 입력값을 표준 정규화를 시킴으로서 network가 각 input neuron에 대한 최적의 parameter를 보다 빠르게 학습할 수 있습니다.
또한, input data가 대략 (-1,1)에 속해있는지 확인하는 것도 유용하다고 합니다.
컴퓨터는 정말 크거나 작은 숫자에 대해 연산을 수행할 때 정확도를 잃으며, 일반적인 (-1,1) 범위와 완전히 다른 척도에 있는 경우 신경망의 기본 parameter가 data에 적합하지 않을 수 있습니다.
이미지의 경우 픽셀의 범위가 0과 1로 제한되도록 1/255로 조정하는 것이 일반적입니다.
Batch Normalization
Normalization가 왜 필요한지에 대해 앞에서 살펴보았습니다.
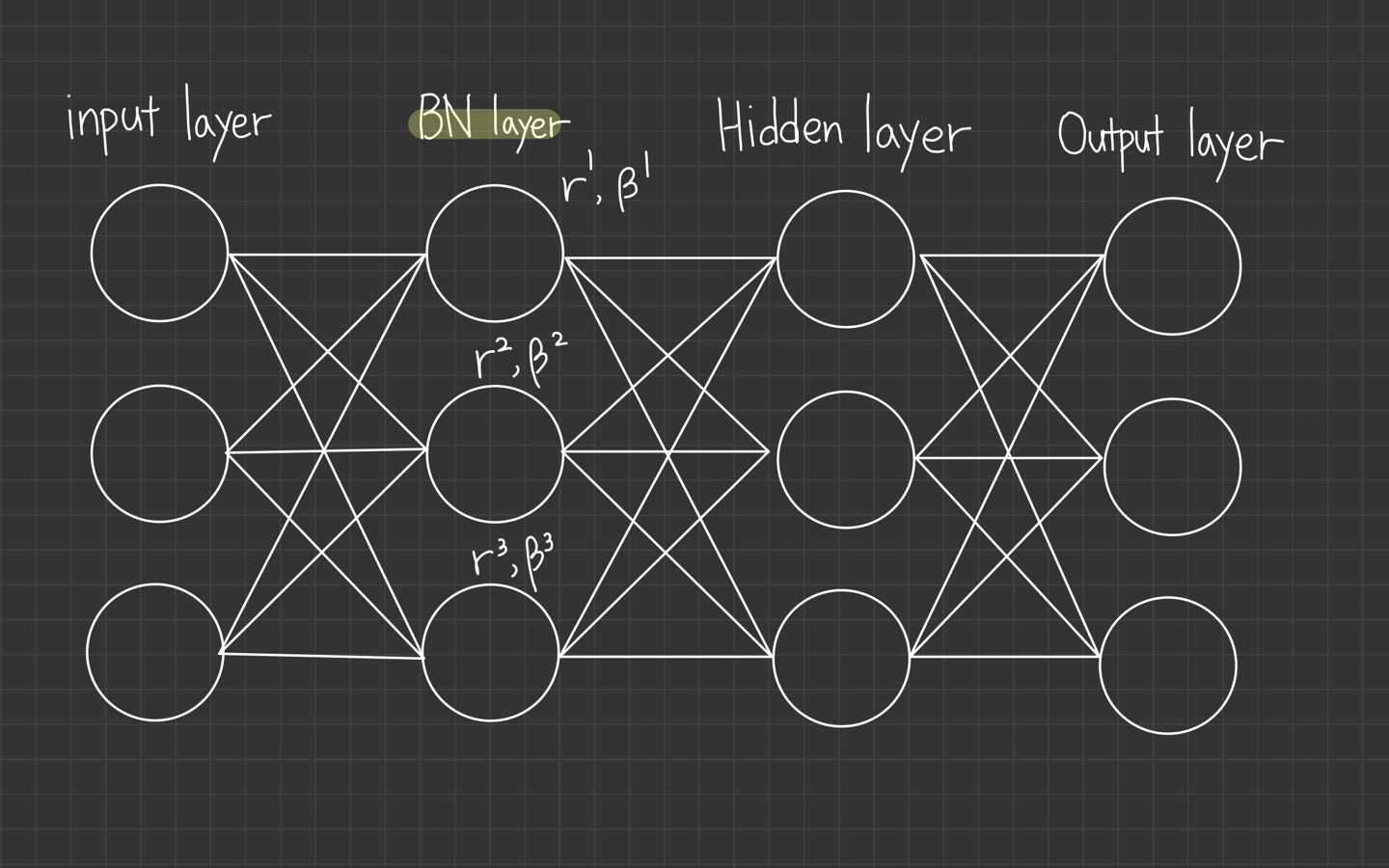
Normalizing inputs improves loss function topology proimarily in these dimensions
input을 정규화하면 network가 첫 번째 layer에서 parameter를 더 효과적으로 학습합니다.
network의 두 번째 layer가 첫 번째 layer의 activation values를 inputs으로 받아들이기 때문에, 이전 layer에서 설정한 정규화된 값을 network에서 더 효율적으로 학습하는데 도움이 된다고 봅니다.
하지만 앞의 예시에서는 Deep Neural Network를 사용할 때, hidden layer에 대한 input distribution은 더 이상 정규화된 분포가 아니며, parameter update로 인해 변경됩니다.
그래서 Batch Normalization의 개념은 모든 hidden layer에 대한 입력 분포가 정규화되도록 하는 아이디어입니다.
모든 layer는 연결하는 weight에 대한 학습 향상을 위해 각 계층의 actiavations을 normalize함으로써 hidden layer에서 더 유용하게 작동하게 합니다.
즉, 각 layer를 normalization하는 것입니다.
이런 이론을 바탕으로 더 깊은 network를 빠르게 training 할 수 있게 되었습니다.
이건 이전 layer의 parameter가 update될 때 활성화 분포가 이동하지 않도록 막습니다.
Internal Covariate Shift
Batch Normalization의 implementation에 대해 살펴보겠습니다.
Deep Neural Network의 Training은 이전 layer의 parameter가 update됨에 따라 각 layer의 입력 분포가 변경됩니다.
이것은 더 낮은 learning rate와 더 신중한 weight initialization을 필요로 하여 training time을 늦추고, saturating non-linearities로 model의 training을 방해합니다.
이 현상을 internal covariate shift이라 하며, layer inputs을 normalize하여 문제를 해결합니다.
잠시 개념을 정리하겠습니다.
neural network의 hidden layer마다 입력되는 값의 분포가 달라지는 현상을 ICS(Internal Covariate Shift)라고 합니다. (내부 공변량 변화)
이제 진짜 Batch Normalization의 개념이 설명할 겁니다!
그래서 생각한 방법은 정규화를 모델 architecture의 일부로 만들고 각 훈련 mini-batch에 대해 정규화를 수행하여 성능을 냈습니다.
Batch Normalization을 이용하면 훨씬 더 높은 learning rate를 사용하고, Initialization에 대해 덜 민감하게 반응할 수 있습니다.
또한, 정규화 역할을 하여 경우에 따라 Dropout이 필요하지 않을 때도 있습니다.
Batch Normalization에서 Batch는 sample data의 Batch에 대해 zero mean and unit variance normalization이 수행됨을 의미합니다.
Implementaion
Batch Normalization의 구현에 대해 설명하겠습니다.
- Input: Values of over a mini-batch: ; parameters to be learned:
- Output:
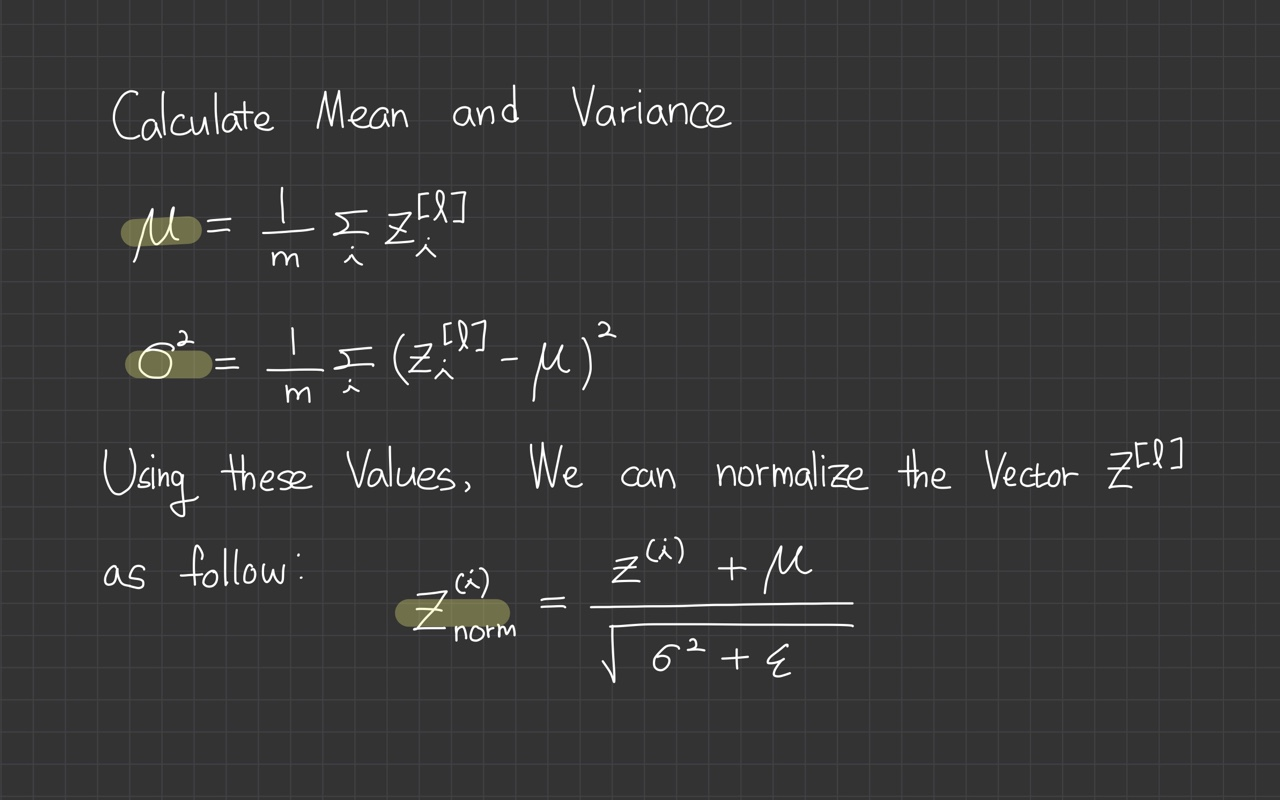
계산식:
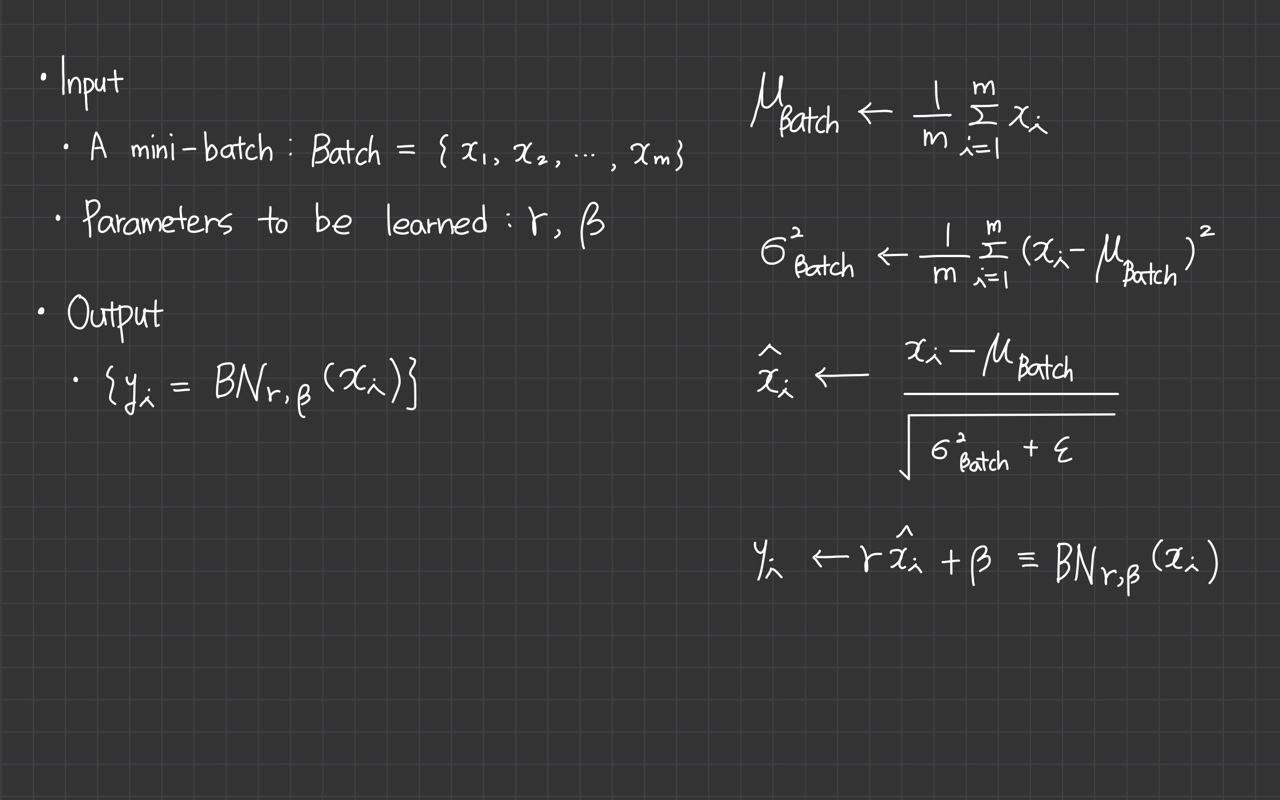
- 로 표시된 데이터의 mini batch가 있습니다. 이 mini batch data의 mean을 계산합니다.
- mini batch data의 variance를 계산합니다.
- 1단계에서 구한 mean을 각 sample data에서 빼주고, 2단계에서 구한 variance를 이용해 standard variance로 나눠줍니다. (variance의 제곱근이 standard variance입니다.) 0으로 나누는 오류 발생을 막기 위해 아주 작은 상수 을 추가합니다.
- 해당 과정을 거치면 mean이 0이 되고 unit variance가 됩니다.
- normalize된 input은 parameter 가 있는 linear function을 통해 전달됩니다. 해당 parameter는 학습 가능한 parameter이며, Batch Normalization을 매우 robust하게 만듭니다.
4번의 과정을 더 살펴보면, z는 zero mean과 unit variance을 갖게 되는데, 이는 사실 일부 sigmoid function 같은 activation function에서는 잘 수행하지 못합니다.
그래서 normalized values를 scaling 해주기 위해 가 필요합니다.
network가 zero mean과 unit variance을 원하지 않는 상황이라 가정하면, 와 를 아래와 같이 학습하여 분포를 복원합니다.
:
: mean(x)
학습 가능한 parameter인 는 문제의 복잡성에 따라 훈련 중에 모든 분포를 학습할 수 있다는 점에서 큰 장점을 가집니다.
각 layer를 단순히 N(0,1)로 정규화하면 non-linear activation function의 영향력이 감소할 수 있는데, 와 가 non-liearity를 유지할 수 있도록 해줍니다.
이를
shift parameter라고도 부릅니다.
따라서 모든 layer에 대해 zero mean, unit variance로 변환하는 것으로 시작하지만, 가 훈련하는 동안 모델에 더 나은 분포를 학습하도록 돕습니다.
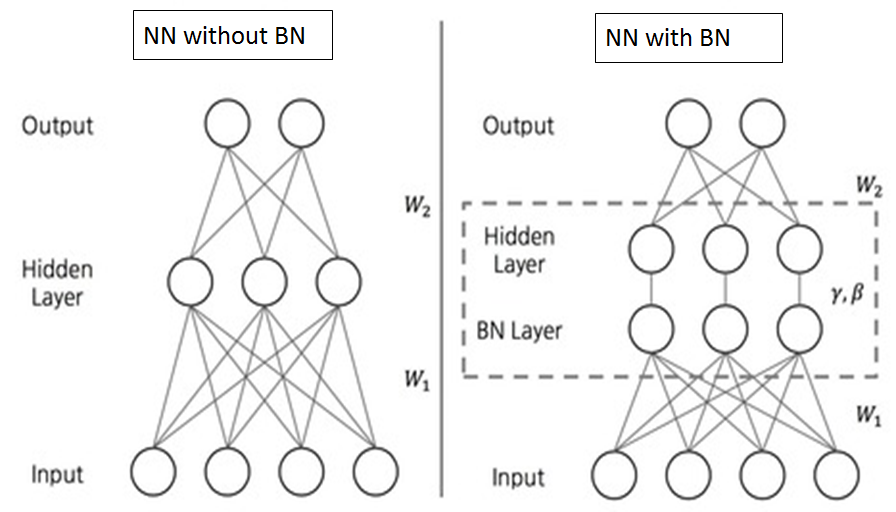
BN에는 학습 가능한 parameter가 있어서 다른 layer라고 봅니다.
keras를 통해 실험한 결과

위의 곡선에서 알 수 있듯이 loss를 0에 가깝게 줄이고, test error의 성능이 향상되었습니다. 이는 일반화의 기능을 보여주었다고 볼 수 있겠네요.
여기까지의 개념을 다시 정리하면, network가 학습에 가장 최적인 분포를 가질 수 있게 layer를 정규화하였습니다.
마지막으로 와 는 각 batch size에 의해 계산되지만, 와 는 모든 batch를 거쳐야 해당 parameter가 학습됩니다.
Not use bias
Batch Normalization의 결과값은 이미 parameter를 사용해 정규화된 z 값을 이미 이동하고 있다는 점을 감안하면, 이 layer에 대한 bias가 필요하지 않음을 알 수 있습니다.
batchnorm은 mean 값으로 activation을 이동합니다.
이에 대한 자세한 내용은 Reference에 있는 논문에 나옵니다.
bias와 유사하게 기능하는 shift parameter를 도입하기 때문에 neural network에서 bias의 필요성이 제거됩니다.
bias term은 각 node에서 작용하는데 반면 batch normalization의 shift parameter는 모든 활성화에 적용됩니다.
activation 자체가 자체 parameter 에 의해 이동하기 때문에, bias가 필요하지 않음을 설명합니다.
더 쉽게 설명해보자면 batch normalization에는 이미 bais term이 포함되어 있습니다.
gamma * normalizied(x) + bias따라서 Conv layer에도 bias term을 추가할 필요가 없다고 하네요.
Summary
배치 정규화의 장점은 학습 속도를 빠르게 올리고, 가중치 초기화에 대한 민감도를 감소 시키며, 모델을 일반화하는 효과가 있습니다.
- training faster
- local minima에 빠지는 것을 막음
- better error surface
- 낮은 loss(낮은 training, test error로 converge)
