개념 내용과 이미지 출처: 딥러닝 교과서
학습(learning)
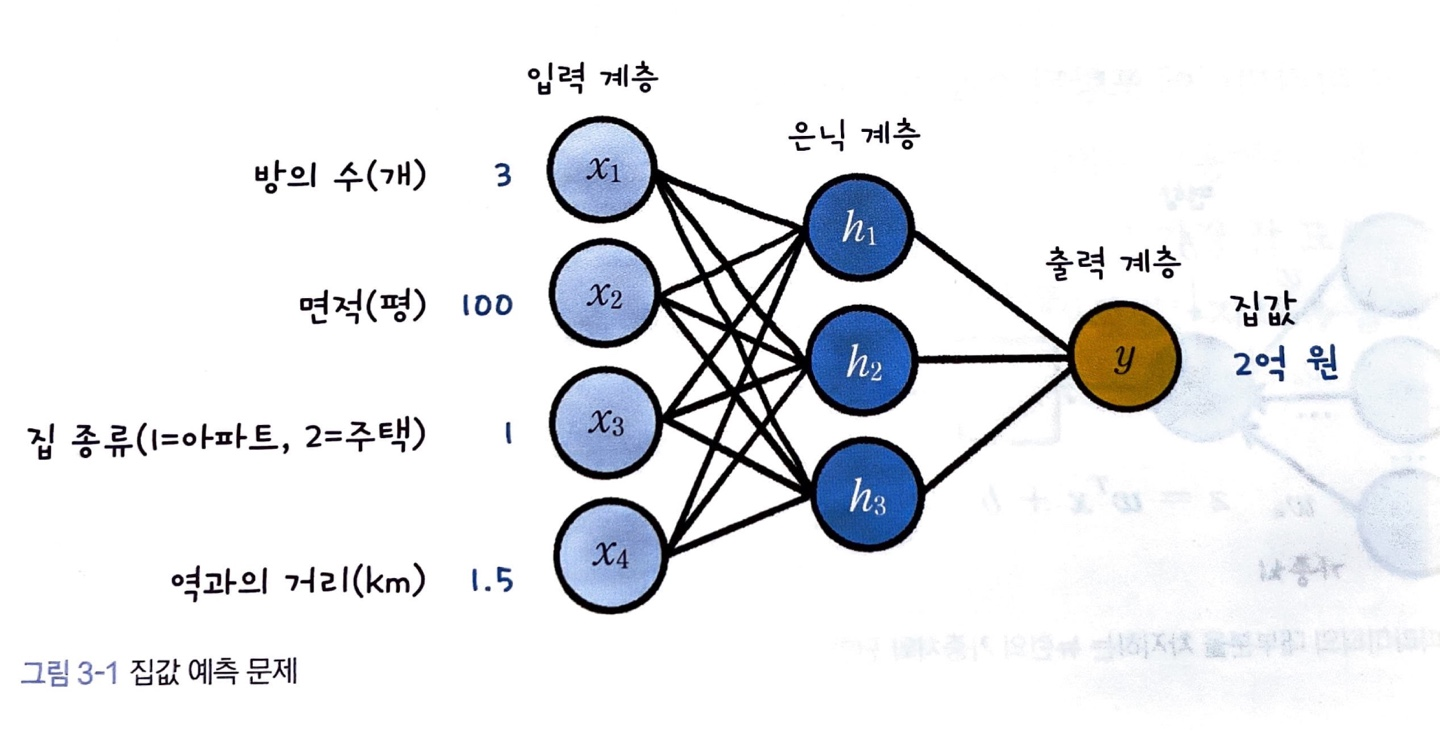
신경망을 이용하여 집값을 예측한다고 가정해봅시다.
신경망에는 집값 예측을 위한 '방의 수, 면적, 집 종류, 역과의 거리'와 같은 입력 데이터와 모델이 예측해야 할 '집값' 데이터인 타깃 데이터가 제공될 뿐, 추론을 위한 규칙은 제공되지 않습니다.
따라서 신경망은 입력 데이터가 들어와도 어떤 출력을 만들어야 할지 모르며, 그 규칙을 학습 데이터를 이용해서 찾아야 합니다.
신경망이 학습한다는 것은 규칙을 찾는 과정을 말합니다.
입출력의 매핑 규칙
신경망에 입력 데이터가 들어왔을 때 어떤 출력 데이터를 만들어야 할지를 정하느 ㄴ규칙은 함수적 매핑 관계로 표현됩니다.
가중 합산과 활성 함수가 연결되어 뉴런을 구성하고, 뉴런이 모여 계층을 구성하며, 계층이 쌓어 신경망의 계층 구조가 정의됩니다.
이처럼 신경망의 요소들이 이루는 복잡한 신경망의 계층 구조 자체가 신경망의 함수적 매핑 관계를 표현하는 것입니다.
신경망의 학습 과정에서 함수적 매핑 관계를 표현하는 전체 계층 구조를 찾아야 하는 것은 아닙니다.
신경망의 구조와 관련된 것은 학습 전 미리 정해두고, 학습 과정에서는 모델 파라미터의 값을 찾습니다.
인공 신경망에서 인공 뉴런의 구조는 사전에 결정하고 학습 과정에서 뉴런의 연결 강도를 포함한 모델 파라미터를 조절합니다.
뉴런의 연결 강도를 결정하는 가중치와 편향은 모델 파라미터의 대부분을 차지합니다. 그 외 활성 함수와 모델 구조와 관련된 파라미터들, 정규화 기법과 관련된 파라미터들, 모델 학습과 관련된 파라미터들이 모델 파라미터에 포함됩니다.
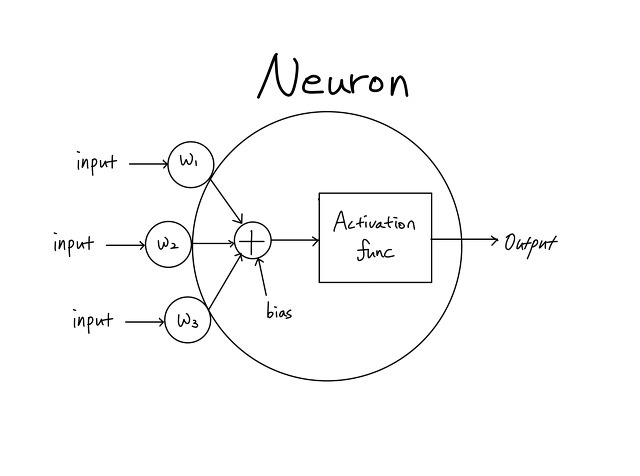
입출력의 매핑 규칙에서 학습해야 할 것들
위의 집값 예측 문제로 돌아오겠습니다.
신경망에서 데이터가 입력되고 '집값'을 예측하는 규칙을 학습을 통해 만들려고 합니다. 이 규칙이 만들어지면 모델은 집값을 예측할 수 있는 추론 능력이 생겼다고 볼 수 있습니다.
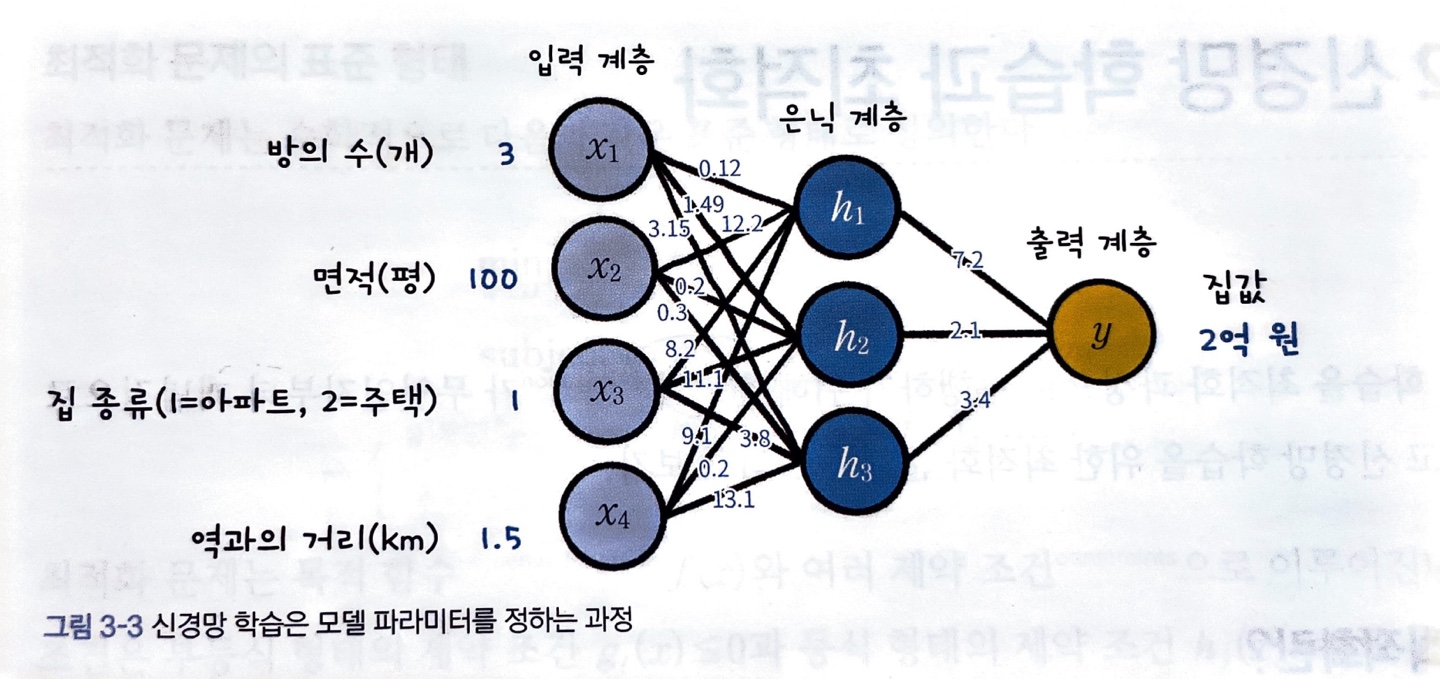
위의 그림처럼 모든 뉴런의 가중치와 편향이 결정될 때 규칙이 완성됩니다.
따라서 학습 과정에서 더 정확한 집값 예측을 위해 신경망 모델의 가중치와 편향을 조정해 나가며, 최적 값이 결정되면 모델은 집값을 예측할 수 있는 추론 능력을 갖게 됩니다.
신경망 학습은 아까 모델의 파라미터값을 찾는 과정이라 했는데, 최적의 파라미터를 찾기 위한 과정을 최적화(optimization) 기법이라고 합니다.
최적화 기법은 함수의 해를 근사적으로 찾는 방법으로 관측 데이터를 가장 잘 표현하는 함수가 되도록 만들어줍니다.
최적화(optimization)
최적화란 유한한 방정식으로 정확한 해를 구할 수 없을 때 근사적으로 해를 구하는 방법입니다.
최적화 문제는 수학적으로 아래와 같은 표준 형태로 정의합니다.

최적화를 통해 찾은 의 값을 최적해라고 하며, 최적해애 점점 가까이 가는 상태를 수렴한다고 하고, 최적해를 찾으면 수렴했다고 합니다.
최소화 문제와 최대화 문제
목적 함수의 부호만 바꿔주면 최소화 문제는 최대화 문제가 된다.
문제를 잘 표현할 수 있는 방식으로 정의하면 되고, 최소화 문제에서의 목적 함수는 비용 함수(cost function) 또는 손실 함수(loss function)이라 부릅니다. 최대화 문제에서는 유틸리티(utility function)이라 부릅니다.
신경망 학습을 위한 최적화 문제 정의
회귀 문제
회귀 문제는 타깃과 예측값의 오차를 최소화하는 파라미터 찾기로 정의할 수 있습니다.
회귀에서 손실 함수는 평균제곱오차(MSE: mean square error)로 정의되며 타깃과 예측값의 오차를 나타냅니다.
분류 문제
분류 문제는 확률 모델 관점에서 관측 확률분포와 예측 확률분포의 차이를 최소화하는 파라미터 찾기로 최적화 문제를 정의할 수 있습니다.
분류 문제에서 손실함수는 Cross Entropy로 정의되며, 타깃의 확률분포와 모델 예측 확률분포의 차이를 나타냅니다.
최적화를 통한 신경망 학습
최적화 알고리즘은 어느 위치에서 출발하든 손실 함수의 최소 지점으로 가야 합니다.
최적화 알고리즘마다 최적해가 있으리라 예상하는 방향, 이동 폭은 다 달라집니다.
교재는 최적화 알고리즘은 4장에서 살펴볼 예정이라 합니다.
Summary
- 신경망을 학습한다는 말은 모델의 파라미터 값을 결정한다는 의미이다.
- 모델 파라미터의 대부분은 뉴런의 가중치와 편향이다.
- 모델의 파라미터값이 결정되면 신경망에 입력이 들어왔을 때 어떤 출력을 만들어야 할지에 관한 규칙이 함수적 관계로 표현된다.
- 신경망 학습은 최적화를 통해 실행된다.
- 신경망 학습을 최적화 문제로 정의하면 회귀 문제의 손실 함수는 평균제곱오차로 정의되며, 분류 문제의 손실 함수는 cross entropy문제로 정의된다.
