hidden layer를 설계할 때 선택할 수 있는 활성 함수는 매우 다양합니다.
활성 함수는 크게 sigmoid 계열과 구간 선형 함수로 정의되는 ReLU(Rectified Linear Unit) 계열로 구분할 수 있습니다.
시그모이드 계열은 sigmoid, (하이퍼볼릭 탄젠트)가 있으며, ReLu 계열은 ReLu, 맥스아웃(maxout), ELU가 포함된다.
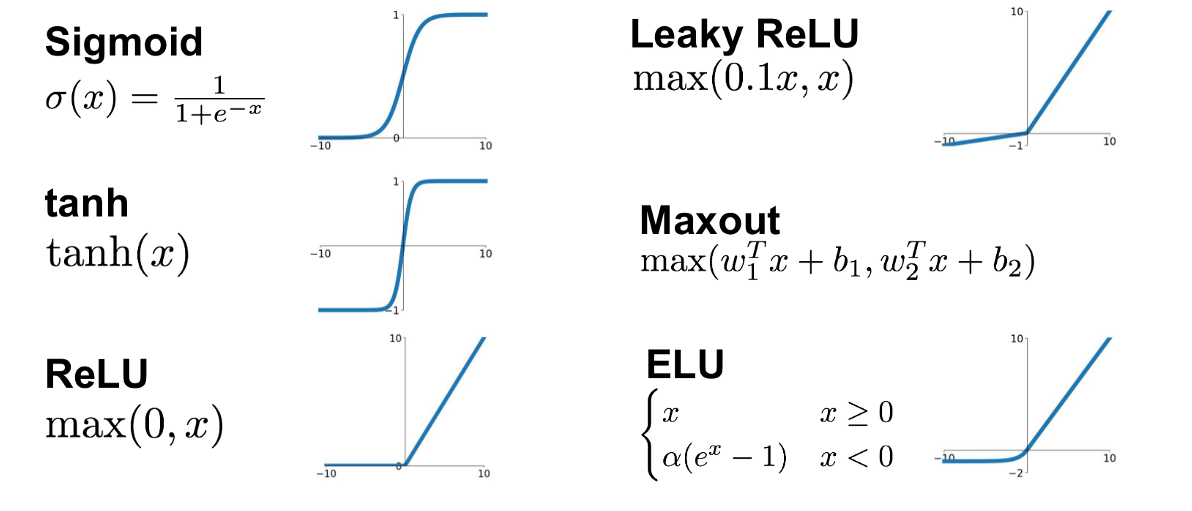
ReLu 계열은 선형성을 갖고 있어서 연산 속도가 매우 빠르고 학습 과정을 안정적으로 만들어줍니다.
따라서 은닉 계층에서는 ReLu 계열을 활성 함수로 사용하는 것이 좋습니다.
시그모이드 계열은 연산 속도도 느리고 그레디언트 소실의 원인이 되어 신경망 학습에는 좋지 않지만, 값을 고정 범위로 만들어주는 기능이 필요한 구조에서 다양하게 활용됩니다.
계단 함수(step function)
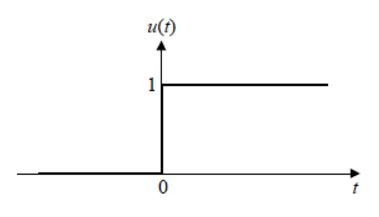
뉴런의 활성과 비활성 상태를 숫자 1과 0으로 표현합니다.
입력값이 0보다 크면 1, 작으면 0을 출력합니다.
계단 함수는 모든 구간에서 미분값이 0이다. 그래서 현대의 신경망에서는 사용이 어렵습니다.
미분을 이용해서 학습하는 역전파 알고리즘에 적용할 경우, 학습이 진행되지 않기 때문인데요.
그래서 역전파 알고리즘을 만들 당시 계단 함수를 대체할 미분 가능한 함수가 필요했습니다.
시그모이드 함수(sigmoid function)
시그모이드는 다음과 같은 S자 형태의 함수입니다.
계단 함수와 같이 값의 범위도 [0, 1]입니다.
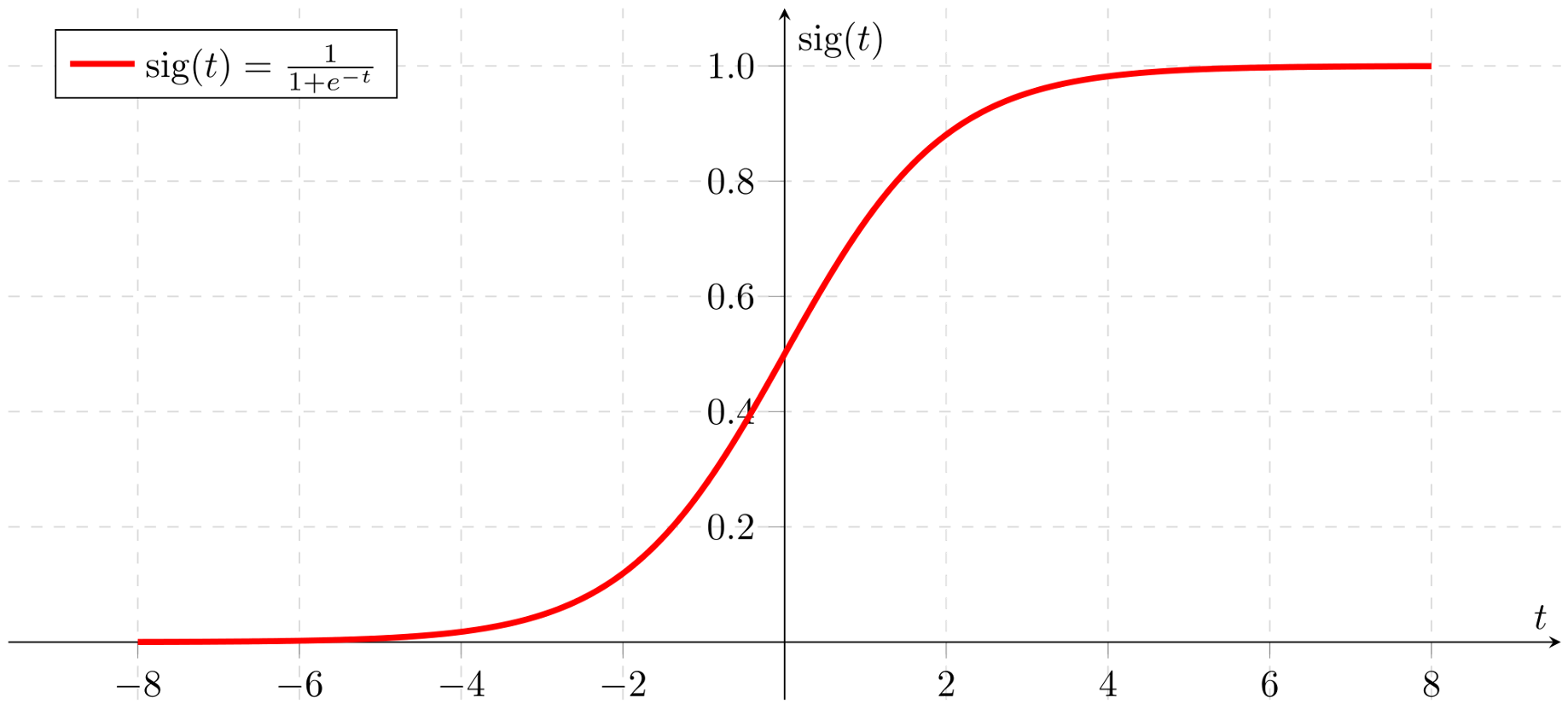
시그모이드는 오랫 동안 activation function으로 활용되었지만 몇 가지 문제점이 있습니다.
- 함수 정의에 지수 함수가 포함되어 있어서 연산 비용이 많이 든다.
- 그레디언트 포화가 발생해서 학습이 중단될 수 있다.
- 양수만 출력하므로 학습 경로가 진동하면서 학습 속도가 느려진다.
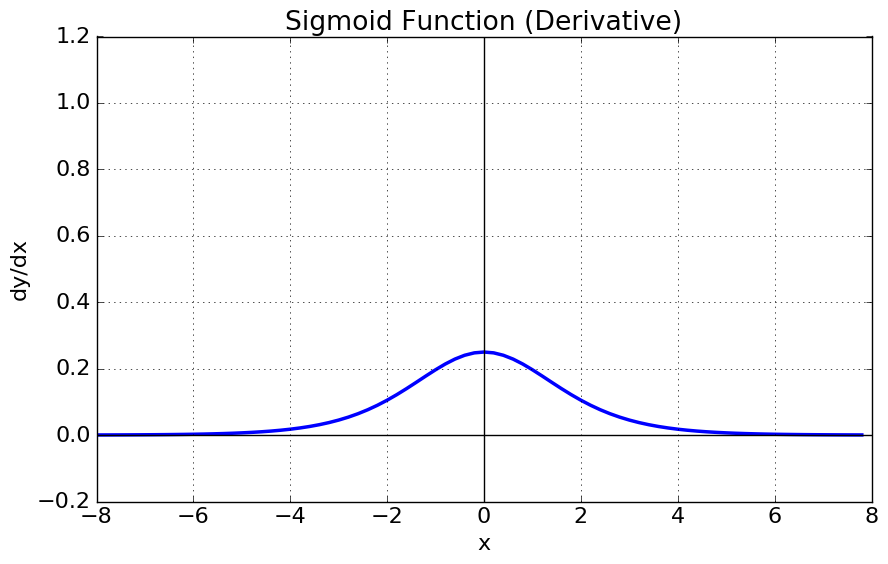
시그모이드 함수를 미분하는 경우 해당 그래프로 변화합니다.
양쪽 끝에서 함숫값이 0과 1로 포화하기 때문에 미분값도 0으로 포화합니다.
시그모이드 함수 끝부분에서 미분값이 0으로 포화되는 그레디언트 포화 상태가 일어납니다.
하이퍼볼릭탄젠트 함수()
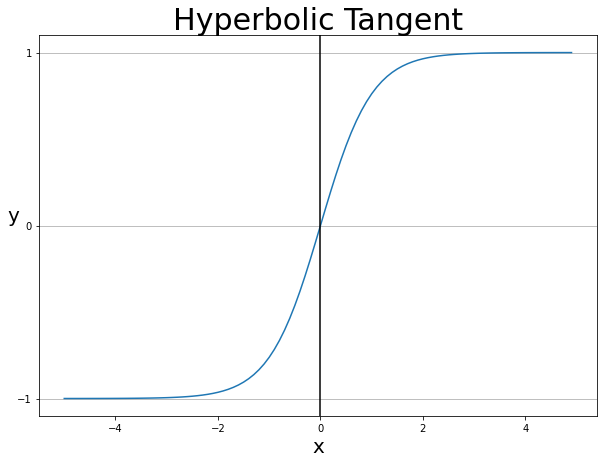
는 함숫값이 [-1, 1] 범위에 있는 S형 함수입니다.
시그모이드가 항상 양수만을 출력하기 때문에 최적화가 비효율적으로 진행되는 문제를 해결하고자 쓰이기 시작했습니다.
하이퍼볼릭 탄젠트는 시그모이드 함수의 선형 변환식으로 나타낼 수 있습니다.
그래서 시그모이드 함수의 문제점인 그레디언트 포화의 문제점이 그대로 남아 있습니다.
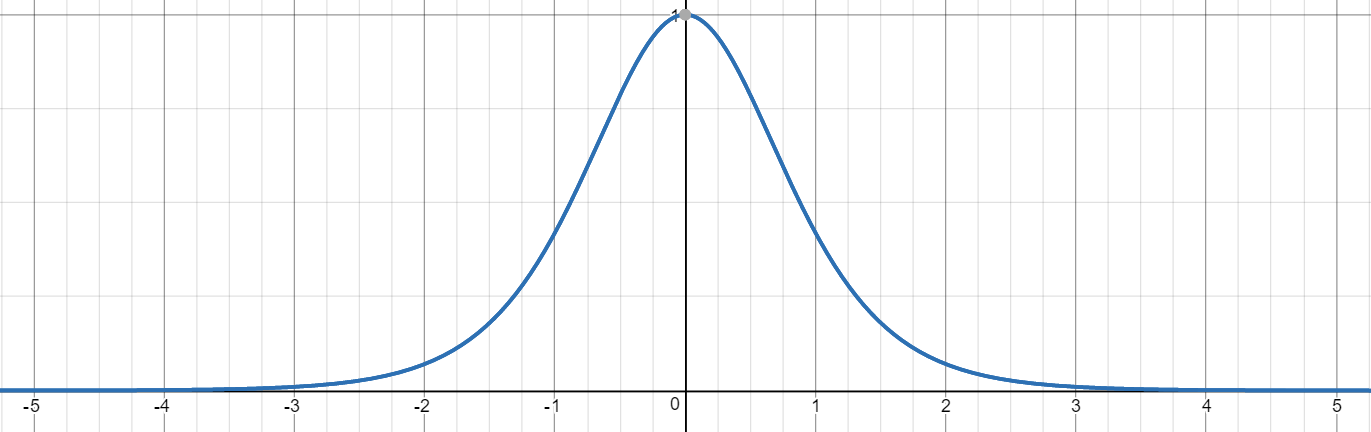
ReLU 함수
ReLU는 0보다 큰 입력이 들어오면 그대로 통과시키고 0보다 작은 입력이 들어오면 0을 출력하는 함수입니다.
따라서 입력값이 양수인 경우에만 활성 상태가 됩니다.
ReLU는 시그모이드 계열보다 추론과 학습 속도가 빠르고 안정적입니다.
그 이유는 연산이 거의 없기 때문인데요. 양수 구간 값을 그대로 통과 시키므로 연산이 필요 없습니다.
음수 구간도 0을 출력하므로 연산이 발생하지 않습니다. 음수 구간의 데이터가 0이 되면서 데이터가 sparse 해져서 추가 연산량이 줄어듭니다.
또한, 미분값이 양수는 1, 음수는 0이므로 학습이 빠릅니다.
ReLU는 양수 구간이 선형 함수이기 때문에 그레디언트 소실이 생기지 않아 안정적으로 학습이 가능합니다.
죽은 ReLU
죽은 ReLU는 뉴런이 계속 0을 출력하는 상태를 말합니다.
그레디언트도 0이 되어 뉴런이 더 학습하지 않고 같은 값을 출력합니다.
이 경우는 가중치 초기화를 잘못했거나 학습률이 매우 클 때 발생합니다.
Leaky ReLU, PReLU, ELU 함수
죽은 ReLU 문제 해결을 위해 음수 구간이 0이 되지 않도록 약간의 기울기를 줍니다.
그 경우가 Leaky ReLU입니다.
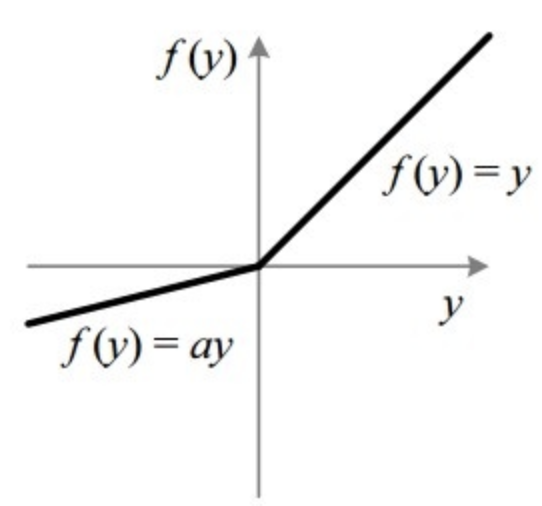
음수 구간에 기울기를 줘서 그레디언트가 생겨 학습 속도가 빨라집니다.
다만, Leaky ReLU는 기울기가 고정되어 있어서 최적의 성능을 내지 못합니다.
기울기 a를 0.01로 고정합니다.
그래서 기울기를 학습하도록 나온 것이 PReLU이며, 뉴런별로 기울기를 학습하므로 성능이 개선됩니다.
ReLU나 PReLU는 음수 구간이 직선이므로 기울기가 작더라도 큰 음숫값이 들어오면 출력값이 마이너스 무한대로 발산할 수 있습니다.
이에 반해 ELU(Exponential Linear Units)는 음수 구간이 와 같이 지수 함수 형태로 정의되어 x값이 음수 방향으로 커지더라도 함숫값이 0에 가까운 일정한 음숫값으로 포화합니다.
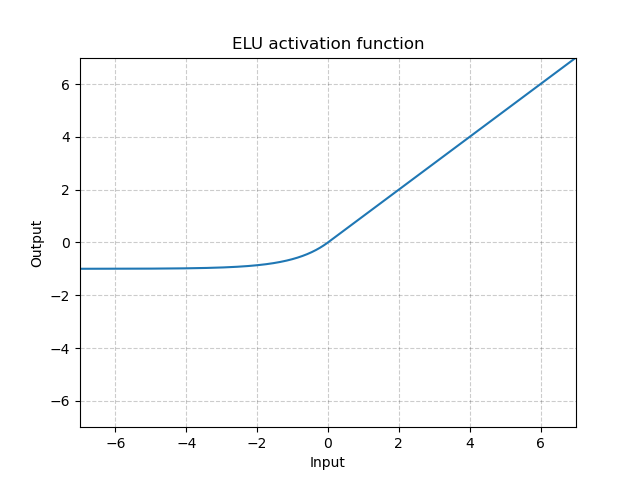
따라서 아주 큰 음숫값이 입력되더라도 함숫값이 커지지 않으므로 노이즈에 덜 민감해집니다.
맥스아웃 함수(maxout function)
maxout은 활성 함수를 구간 선형 함수(piecewise linear function)로 가정하고, 각 뉴런에 최적화된 활성 함수를 학습을 통해 찾아냅니다.
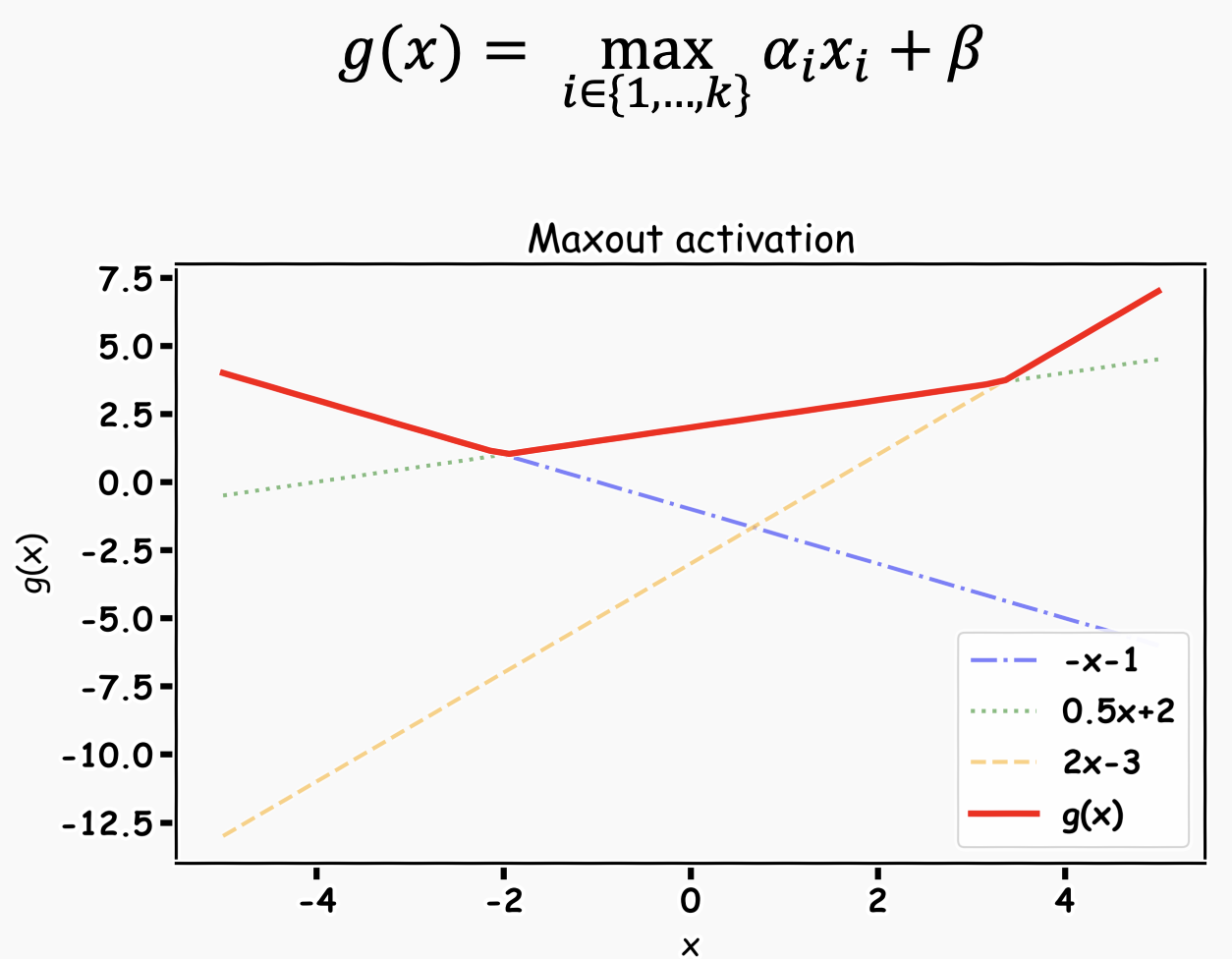
다음 그림과 같이 뉴런별로 선형 함수를 여러 개 학습 시킨 뒤 최댓값을 취하면 빨간 선이 나옵니다.
맥스아웃은 ReLU의 일반화된 형태라고 볼 수 있으며 성능이 뛰어납니다.
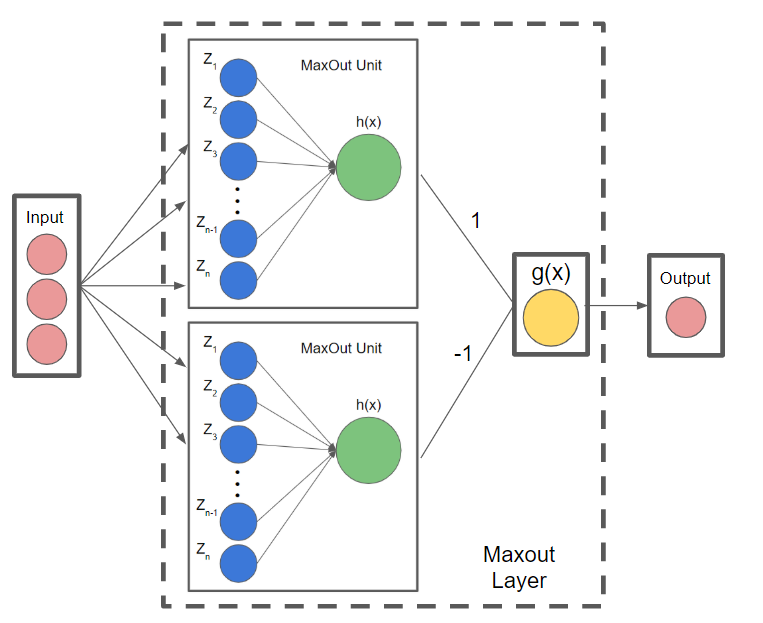
maxout 유닛 구조를 같이 보겠습니다.
맥스아웃 활성 함수를 학습 시키기 위해 뉴런을 확장한 구조를 맥스아웃 유닛이라고 합니다.
맥스아웃 유닛은 선형 함수를 학습하는 선형 노드와 최댓값을 출력하는 노드로 구성됩니다.
선형 노드는 뉴런의 가중 합산과 같은 형태로 선형 함수를 학습하며, 최댓값 출력 노드는 구간별로 최댓값을 갖는 선형 함수를 선택합니다.
위에는 맥스아웃 유닛이 두 개 있는 2계층 신경망입니다.
까지 최댓값을 출력하는 H1 노드로 구성됩니다.
따라서 m개의 선형 함수를 학습해서 m개의 구간으로 정의되는 구간 선형 함수를 만듭니다.
볼록 함수 근사 능력
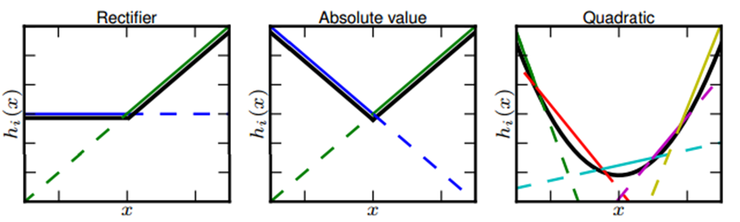
맥스아웃은 선형 노드의 개수에 따라 다른 형태의 볼록 함수를 근사합니다.
다음과 같이 선형 노드가 2개라면 ReLU와 절댓값 함수를 근사할 수 있고,
선형 노드가 5개면 2차 함수를 그낫할 수 있습니다.
선형 노드가 많아질수록 조금 더 부드러운 곡선 형태의 활성 함수를 학습할 수 있지만,
맥스아웃 유닛에 사용되는 파라미터 수가 노드의 개수에 비례해서 증가하므로 선형 노드를 제한적으로 늘려줘야 합니다.
맥스아웃을 적용하면 유닛별로 사용되는 파라미터 수는 증가되지만, 신경망의 깊이를 줄일 수 있어서 전체적인 파라미터 수는 소폭 증가합니다.
Swish 함수
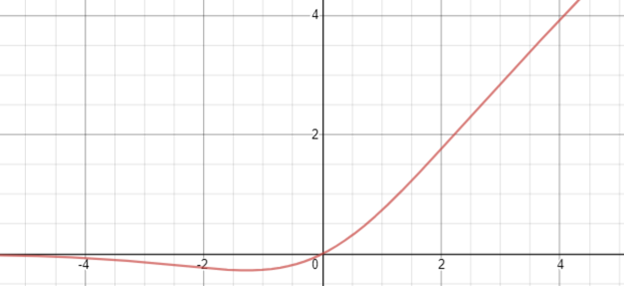
swish 함수는 선형 함수 와 시그모이드 의 곱인 로 정의됩니다.
ReLU나 ELU와 비슷한 모양이지만 원점 근처의 음수 구간에서 잠시 볼록 튀어 나왔다가 다시 0으로 포화하는 곡선 모양입니다.
지금까지 Neural network에서 hidden layer와 output layer 사이의 activation function의 종류에 대해 알아보았습니다!
결론적으로는 위와 같이 여러 종류의 활성화 함수가 있는데 어떤 활성화 함수를 사용해야 할까요?
가장 많이 사용되는 함수는 ReLU입니다. 간단하고 연산량도 적어 우선적으로는 'ReLU'를 사용합니다.
ReLU 다음에 Leaky ReLU 등 ReLU 계열의 다른 함수도 사용해봅니다.
는 잘 사용하지 않습니다. 도 좋은 성능을 보이진 못합니다.
