[Linear Algebra] Linear independence, Span, Basis, Dimension

Lecture 9 선형독립(Linear independence), Span, 기저(Basis) 그리고 차원(Dimension)

저는 위 블로그를 참고하여 그대로 정리하였습니다. Gilbert Strang 교수의 Linear Algebra 강의를 정리한 포스팅입니다. 굉장히 정리가 잘 되어 있어서 강추합니다!

저는 단순히 내용을 그대로 따라 적으며 정리하였으며, 그냥 나중에 제가 복습할 때 보려는 용도로 포스팅합니다!

감사합니다.

Linear independence

선형독립의 개념을 이해하기 전에 알고 가야하는 개념을 설명합니다.

$m$x$n$ 사이즈의 행렬 A가 있습니다. 대신 column의 수 n이 row의 수 m보다 큰 경우를 설명합니다.

이 경우에는 미지수의 개수가 방정식의 개수보다 많기 때문에, 행렬 A에 대해 $Ax=0$에 대한 0이 아닌 해가 존재하게 됩니다. 이말은 즉 Null space가 존재한다는 의미입니다.

그리고 여기서 null space를 구하는 방법을 간단히 복습하고 갑니다. 이 내용에 대해 알고 싶다면 해당 포스팅을 참고해주세요.

독립(independence)의 의미

독립에 대한 개념을 정의하자면

vector $x_1, x_2, ..., x_n$이 있을 때, 만약 모든 계수(coefficient)가 0인 경우를 제외하고 어떠한 선형조합(linear combination)으로도 0을 만들 수 없다면 이 벡터들은 독립(independence)이라고 합니다.

그리고 반대의 경우인 종속(dependent)의 개념에 대해 설명하며, 그래프를 통해 예시로 설명합니다.

선형조합(linear combination)

선형조합(linear combination)이라는 것은 사실 벡터는 변함없이 그대로고 상수 c만 바뀌는 경우입니다. 벡터 방향은 변함없고 크기만 바뀌게 되는데, 크기만 조절해서 0을 만들려면 반드시 벡터들의 방향이 같아야만 합니다.

위의 이미지는 독립인 경우의 예시를 들고 있습니다.

또한 2차원 평면(plane)에 벡터가 3개인 경우의 그래프가 나오는데, 이 경우엔 앞에서 설명했던 $m<n$의 경우이며, free variable이 존재하게 됩니다.

어떤 행렬 A의 column vector가 선형 독립(linear independent)이기 위해서 A에 대한 Null space가 오직 변수가 0인 경우에 대해서만 존재해야한다. ($x_1=0, x_2=0, ..., x_n=0$)

어떤 행렬 A에 대해서 $Ax=0$ 식에 대한 Null space가 $x_1=0, x_2=0, ..., x_n=0$과 같이 모든 x가 0일 때를 제외한 다른 경우가 존재한다면, 그 행렬의 comlumn vector는 종속이다.

종속(dependence)의 예시

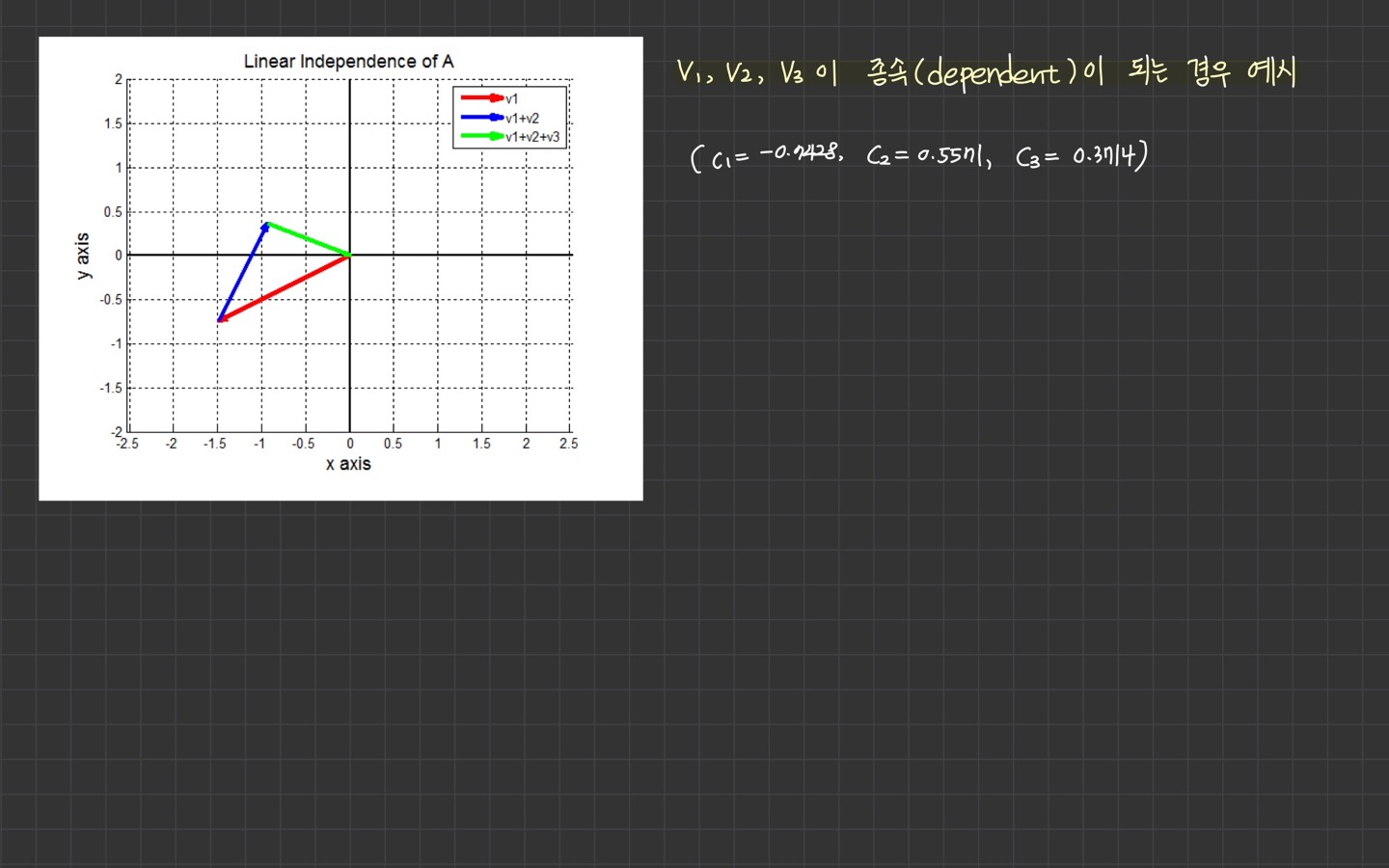
독립(dependence)과 종속(dependence)의 개념

해당 내용을 통해 독립과 종속이 완전히 이해가 되셨으면 좋겠습니다!

Span

• 벡터들로 형성할 수 있는 공간
• $v_1, v_2, ..., v_n$의 선형조합(linear combination)을 통해 만들어지는 공간

vector $v_1, v_2, ..., v_n$이 어떤 공간(space)를 span한다는 의미

• vector $v_1, v_2, ..., v_n$들의 가능한 모든 선형조합으로 공간을 형성하는 것을 의미
• vector들의 모든 가능한 선형조합에 대한 결과 vector들을 한 공간에 몰아 넣은 것을 의미

basis

• vector들은 어떤 공간을 span하면서 그들이 독립(independence)인 vector들을 basis라고 한다.

basis의 조건

• 기저 벡터들은 독립(independent)이다.
• 기저 벡터들은 공간을 span한다.

• standard basis에 대한 개념 설명
• 단위 행렬의 null space는 오직 $[0,0,0]^T$인 zero vector이다.

• (6): $R^3$의 basis가 아님
• (7): $R^3$의 basis가 아님
• (8): $R^3$의 basis임

식 (7)의 시각화

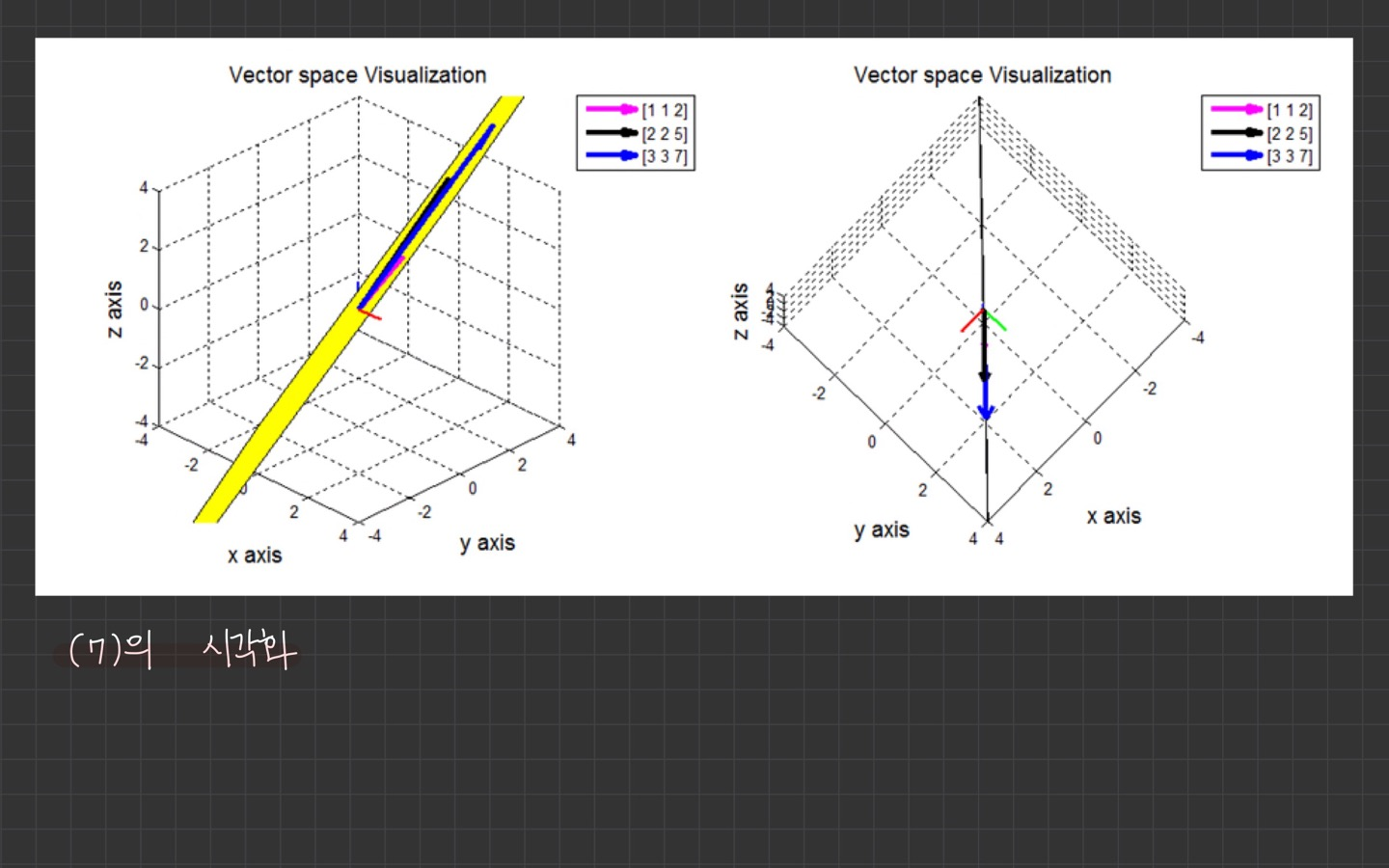
N차원의 basis인지 판단 방법

• basis는 유일하지 않다.

Dimension

주어진 공간(space)들에 대한 모든 기저(basis)들은 같은 수의 벡터를 가진다. 여기서 vector의 수가 그 공간의 차원(dimension)을 의미함

Column space의 차원

$Rank(A)$ = $number$ $of$ $pivot$ $columns$ = $Dimension$ $of$ $C(A)$

Null space의 차원

$dim$ $C(A)$ = $r$
$dim$ $N(A)$ = $number$ $of$ $free$ $variables$ = $n-r$ ...(11)