[Linear Algebra] 고유값(eigenvalue)과 고유벡터(eigenvector)

Lecture 21-(1) 고유값(eigenvalues)과 고유 벡터(eigenvectors)

저는 위 블로그를 참고하여 그대로 정리하였습니다. Gilbert Strang 교수의 Linear Algebra 강의를 정리한 포스팅입니다. 굉장히 정리가 잘 되어 있어서 강추합니다!

저는 단순히 내용을 그대로 따라 적으며 정리하였으며, 그냥 나중에 제가 복습할 때 보려는 용도로 포스팅합니다!

감사합니다.

Eigenvalue and Eigenvector

$Ax$ paralle to $x$ ... (1)

$Ax=\lambda x$ ... (2)

$Ax=\lambda$

고유벡터(eigenvector)

수많은 벡터들 중 어떤 벡터들은 A에 곱해져서 그 위치나 방향이 바뀌어도 원래 자신과 동일한, 혹은 평행한 방향을 가짐

고유값(eigenvalue)

변환 전의 $x$와 A에 곱해져서 변환된 $x$의 크기는 다를 수 있으며, 그 크기는 특정 상수를 곱한 만큼의 차이만 존재. 여기서 크기를 나타내는 특정 상수는 $\lambda$로 표현

the definition of eigenvector

Def.
어떤 선형시스템 방정식(linear system equation) A에 의해 변환되는 수많은 벡터들 중에 곱하기 전과 곱한 후의 벡터 방향이 똑같은 벡터이다.

• 방향은 변하지 않지만 원래의 벡터와 A에 의해 변환된 벡터의 크기가 어떤 상수배만큼 다름. 여기서 상수는 $\lambda$를 의미

2x2 size, Linear system equation

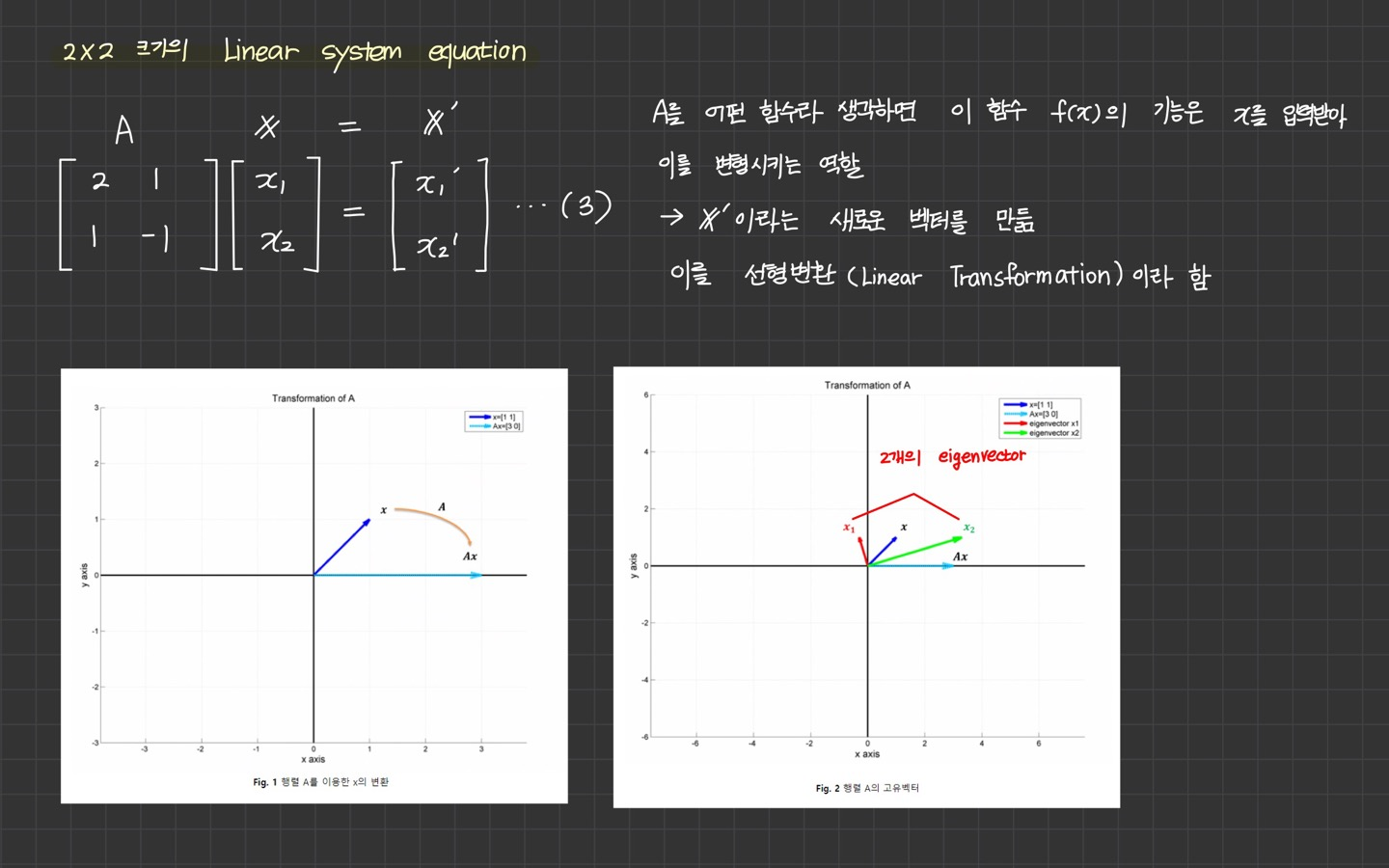
A를 어떤 함수라 생각하면 이 함수 $f(x)$의 기능은 x를 입력받아 이를 변형시키는 역할

$x'$이라는 새로운 벡터를 만듦. 이를 선형변환(linear transformation)이라 함

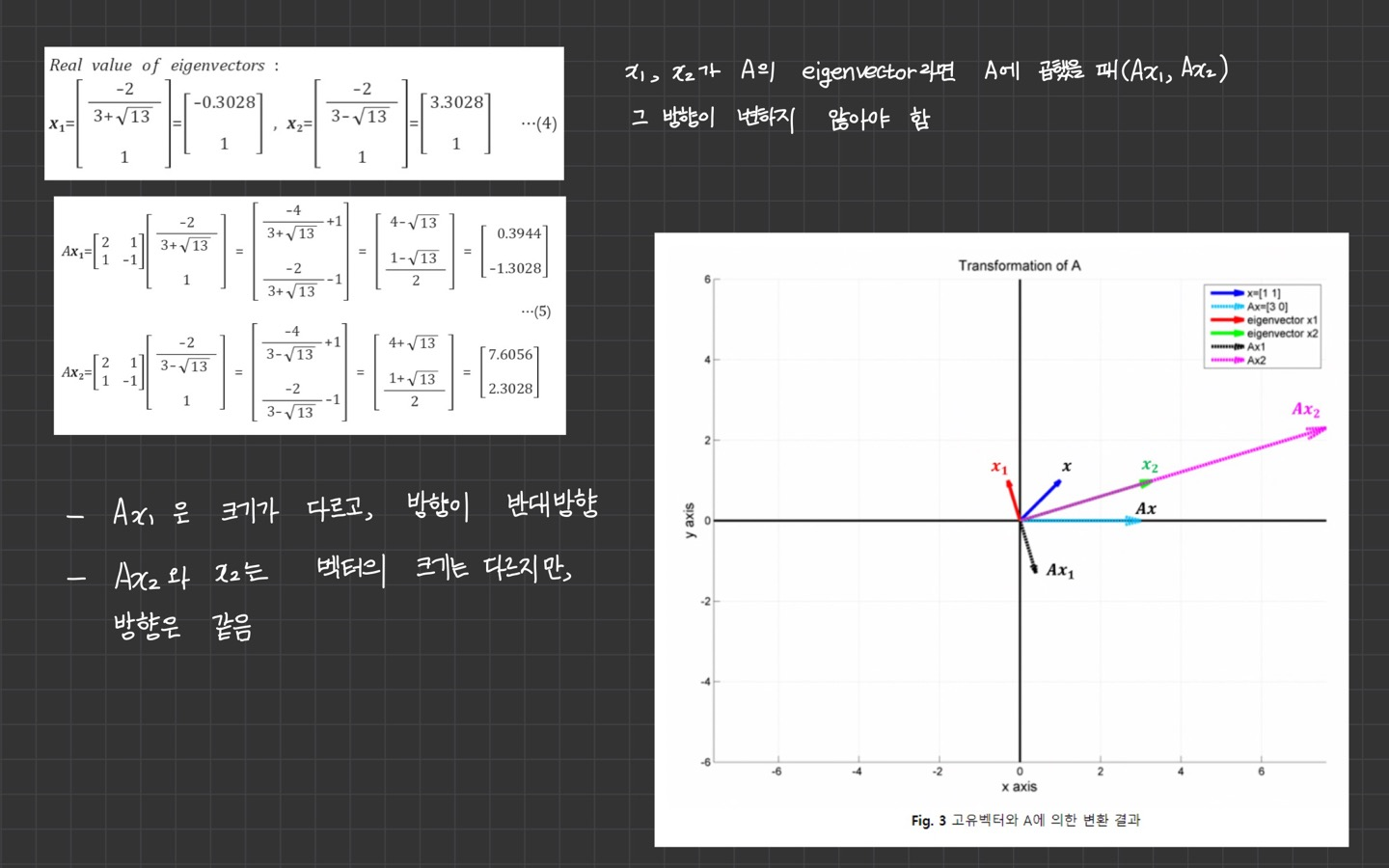
• $Ax_1$는 크기가 다르고 방향이 반대 방향
• $Ax_2$는 벡터의 크기는 다르지만 방향은 같음

eigenvector인가?

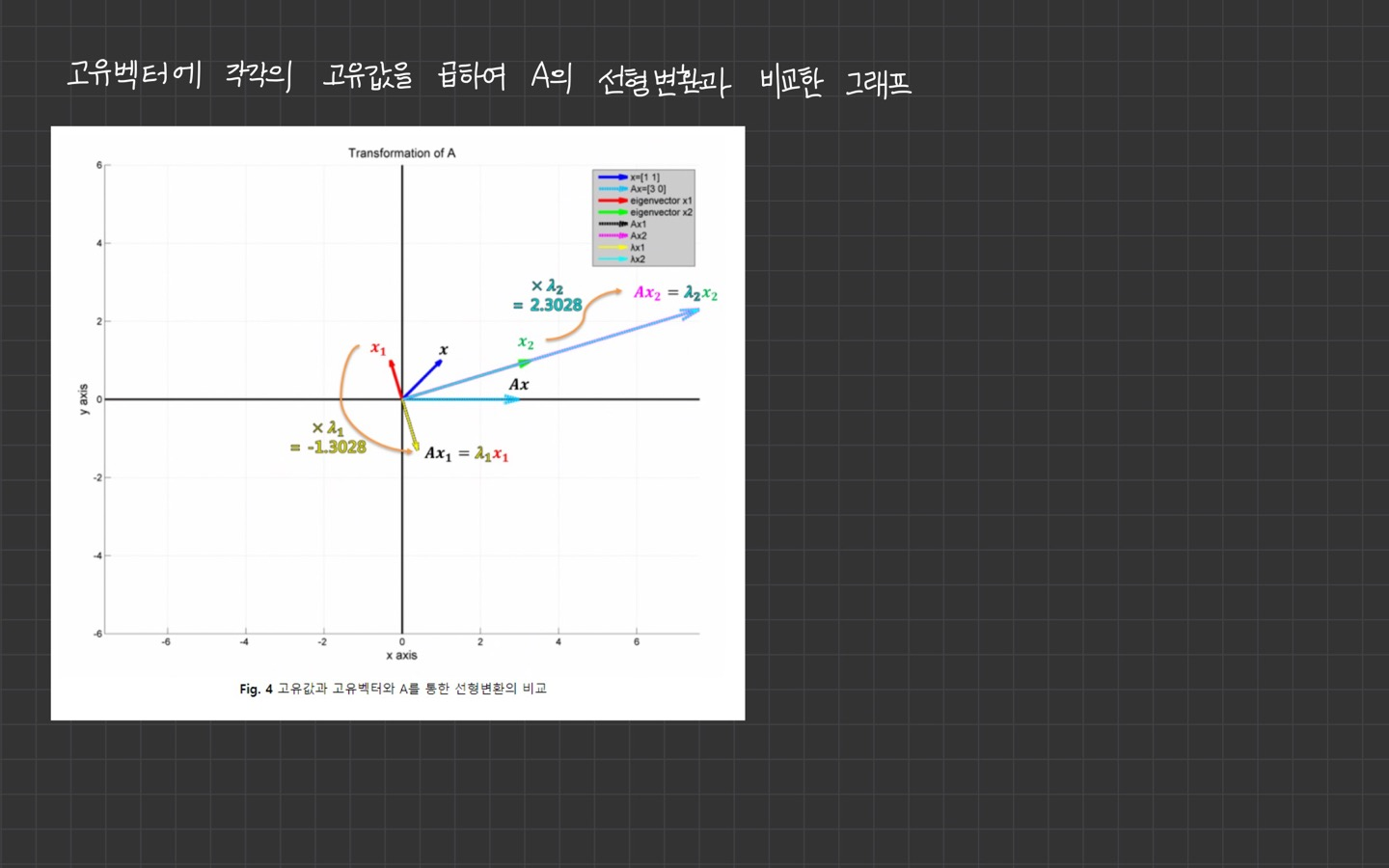
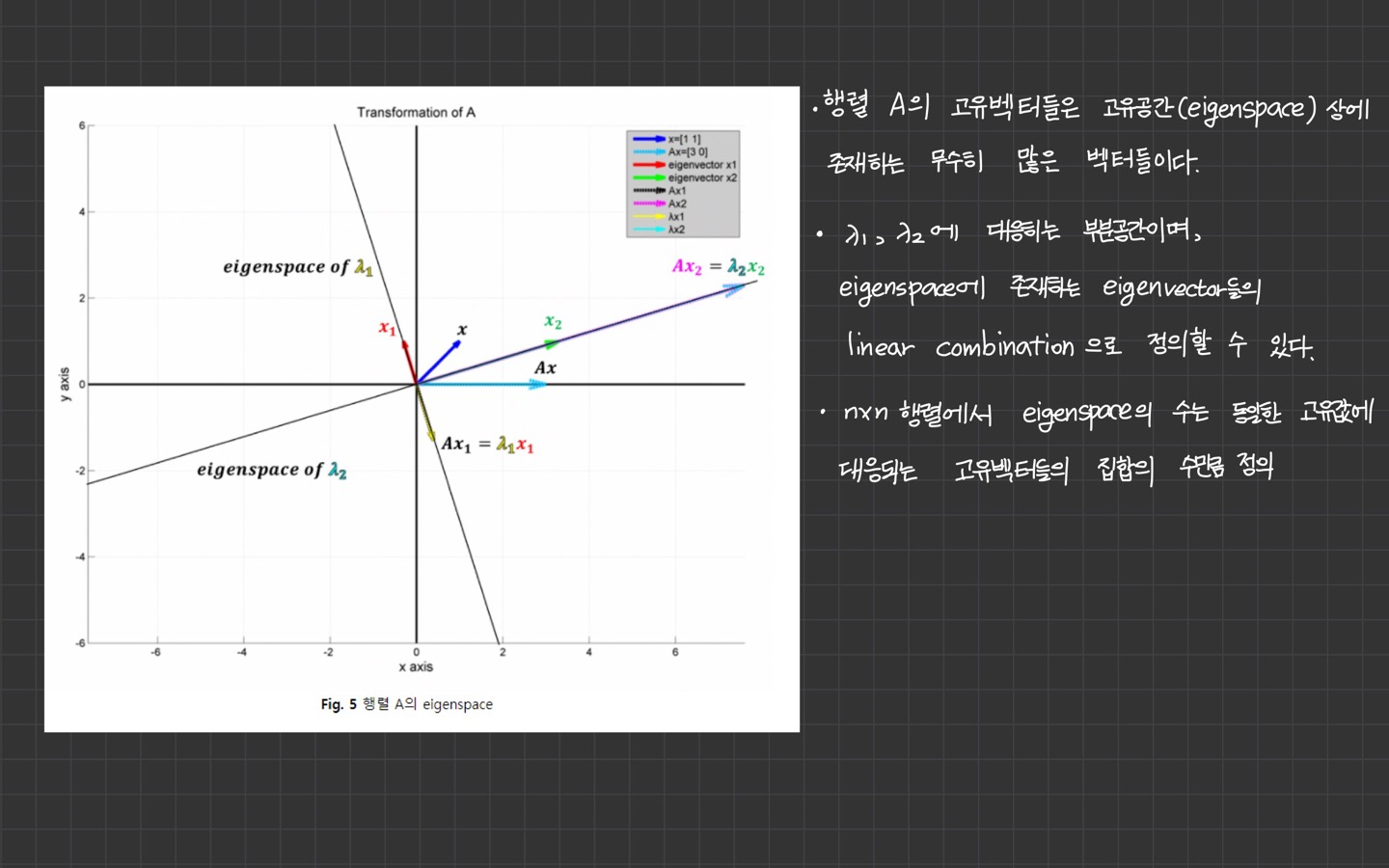
• 고유값을 통해 선형변환 시켜주는 과정