Super Resolution의 문제를 접근하는 방식은 크게 3가지가 있다고 합니다.
- Interpolation-based method
- Reconstruction-based method
- (Deep) Learning-based method
먼저 Interpolation이 무엇인지부터 살펴보겠습니다.
Interpolation에 대한 설명을 참조한 블로그 출처: 여기
Interpolation(보간법)
Interpolation은 보간법이라고도 합니다.
보간법이란? 알려진 값을 가진 두 점 사이 어느 지점의 값이 얼마일지를 추정하는 기법을 의미함
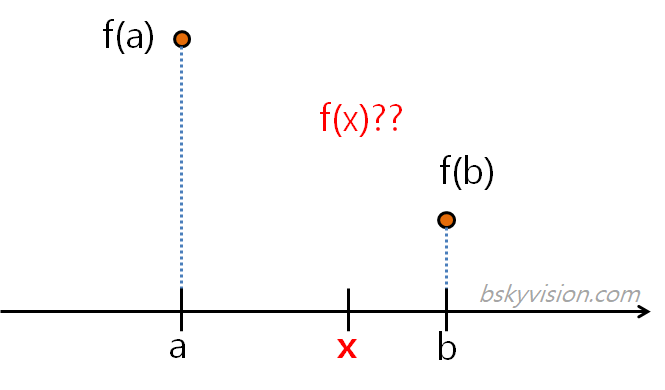
위의 그림을 통해 다시 이해해보자면, a와 b 사이의 x라는 지점의 값이 무엇인지, f(x)를 추정하는 방법입니다.
linear interpolation(선형보간법)
보간법에도 여러가지 접근법이 있다고 합니다. 선형보간법은 아까 보았던 두 점 사이에 직선을 그리는 방법입니다.
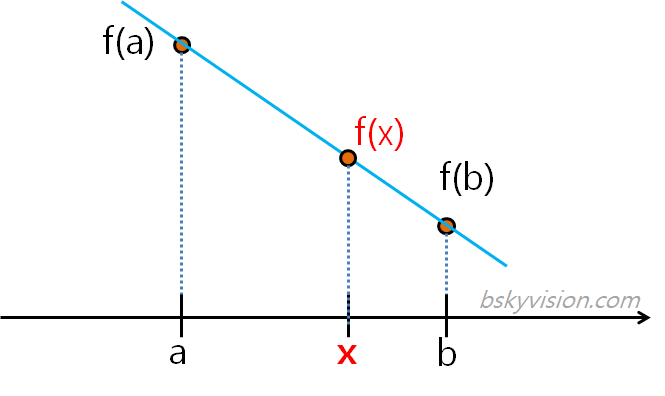
직선은 1차 함수입니다. y=mx+n 식을 이용해서 두 좌표값을 대입시킨다면 그 1차 함수식을 찾아낼 수 있습니다.
1차함수식을 찾아냈다면 f(x)에 좌표값을 대입하여 x의 값을 알아낼 수 있다는 것이 선형보간법의 핵심이라고 합니다.
선형보간법은 두 개의 점을 참조하였습니다.
cubic interpolation(삼차보간법)
선형보간법은 1차 함수를 활용한 보간법이었습니다. 삼차보간법은 3차(cubic) 함수를 사용합니다. 삼차보간법은 a, b가 삼차함수 그래프 위에 있다고 생각합니다.
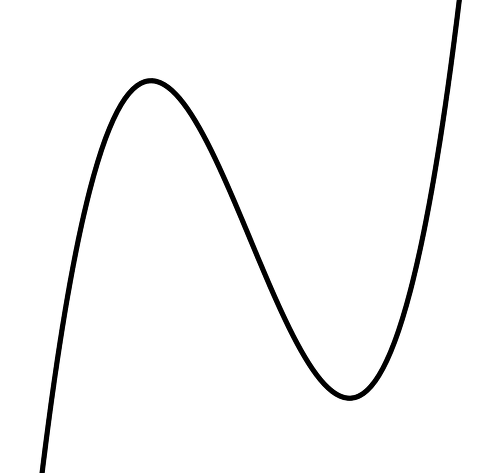
삼차함수는 y=a(x-α)^2(x-β)를 따를 때(α!=β, α>0일 때) 삼차 함수의 가장 일반적인 그래프는 이렇게 생겼습니다.
삼차함수에 지레 겁먹을 필요는 없습니다.😊 그냥 해가 하나 더 늘어났다고 생각하면 편합니다!
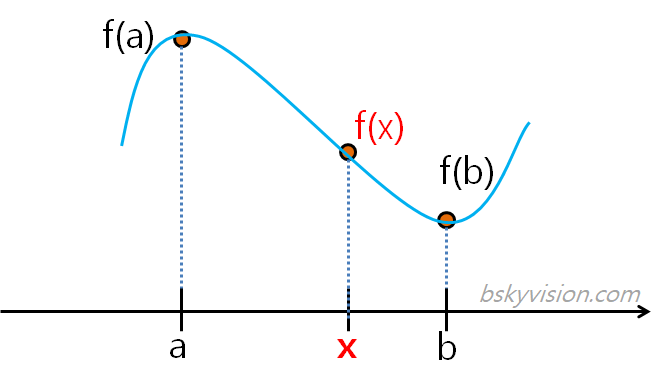
어쨌든 위의 이미지처럼 3차함수를 이용해서 미지의 값을 추정하면 일차함수보다 훨씬 더 부드러운 결과를 만들 수 있습니다.
직선이 아닌 곡선의 이점이라 볼 수 있겠습니다.
대신 f(x)=mx^3+nx^2+jx+k 를 알아내야 합니다. m, n, j, k를 찾아내야 합니다.
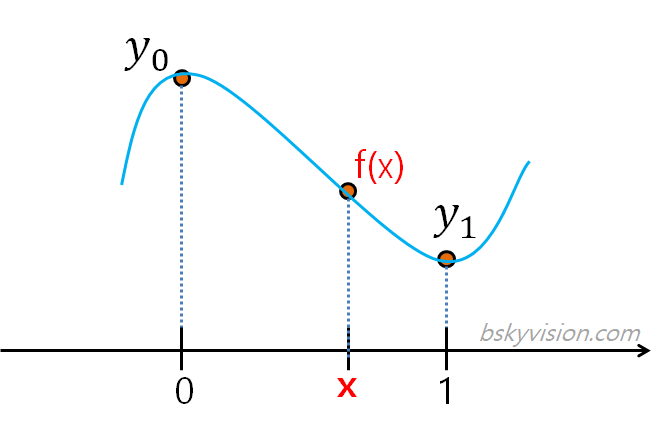
그래서 여기서는 a=0, b=1이라고 가정하였습니다.
그러면 f(0)=y_0, f(1)=y_1이 되겠죠.
f(0)=y_0=k 입니다. ...(1)
f(1)은 y_1이었는데요 식을 정리하면 y_1 = m+n+j+k 가 됩니다.
다시 한 번 정리하면,
y_1-y_0 = m+n+j ...(2)
이제 두 개의 식이 나왔습니다. 3차함수는 3개의 방정식이 나오면 연립방정식으로 풀이할 수 있습니다. 여기서 이제 사용하는 것이 '미분'입니다.
f'(x)=3mx^2+2nx+j
미분식을 구했고 다시 0과 1을 대입해봅시다! 눈으로 수학을 보는 건 원래 어렵습니다.🤣
f'(0) = j ...(3)
f'(1) = 3m+2n+j ...(4)
이제 총 4개의 방정식을 구했습니다. 연립해서 풀면됩니다!
그렇지만 미분에는 특징이 하나 있다면 연속적인 값이라면 미분이 가능하지만, 이산적일 경우엔 미분값을 다른 방식으로 구해야 합니다.
미분을 배워보신 분이라면 당연히 아시겠지만, 미분은 기울기입니다. 도함수의 식을 떠올려 볼까요?
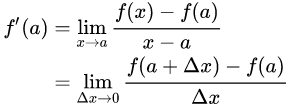
이것은 y의 증가량을 x의 증가량으로 나눠준 것입니다.
그러므로
f'(0) = y1-y(-1)
f'(1) = y_2-y_0/2
입니다.
그래서 참조해야 할 좌표가 늘었습니다. (0,y0), (1, y_1) 외에 (-1, y(-1)), (2, y_2)를 참조해야 합니다.
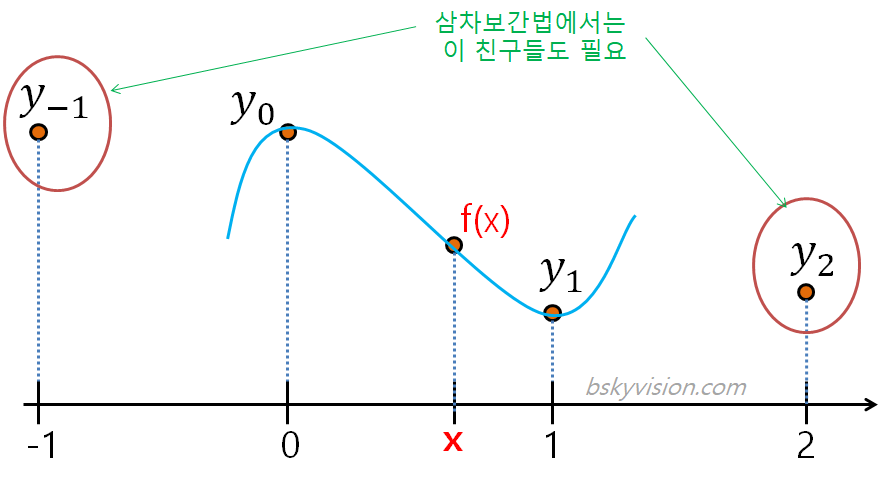
삼차보간법은 이렇게 4개의 이웃점을 필요로 합니다.
이제 f'(0)과 f'(1)을 방정식 (3), (4)에 대입하겠습니다!
j = y1-y(-1)/2
3m+2n+j = y_2-y_0/2
이 나왔습니다. 그럼 j가 y에 대한 식으로 풀렸습니다. 나머지 방정식에 j의 값을 대입하여 정리하면 (직접 하기 귀찮...🙄)
m+n = y(-1)+2y_0+y_1/2
3m+2n = y(-1)-y_0-y_1+y_2/2
이제 m,n에 대한 식이 y로 모두 풀렸으니 m과 n을 정리할 수 있을 것 같습니다.
m = -y_(-1)/2+3/2y_0-3/2y1+y_2/2 ...(2)-2
n = y_(-1)-5/2y_0+2y_1-y_2/2 ...(4)-2
이제 m, n, j, k를 모두 찾아냈습니다!
여기서 중요한 건 삼차함수를 통하여 값을 찾아내었다는 것입니다.
Bilinear Interpolation and Bicubic Interpolation
선형보간법을 2차원으로 확장시킨 것이 bilinear interpolation
삼차보간법을 3차원으로 확장시킨 것이 bicubic interpolation
2차원으로 확장시킨 것 외에 원리상 달라진 것은 없다고 합니다.
쌍선형보간법은 이웃한 4(=2x2)개의 점을 참조하고, 쌍삼차보간법은 16(=4x4)개의 점을 참조합니다.
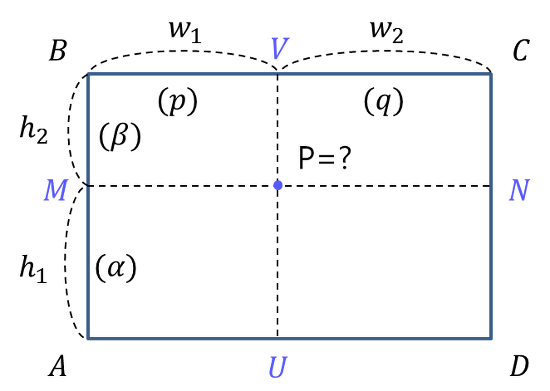
위 그림과 같이 점 P에는 이웃한 4개의 점이 있다는 것을 알 수 있습니다. 사각형 변까지의 거리를 w1, w2, h1, h2로 두고 A, B, C, D의 네 점은, bilinear interpolation에 의해 계산되어 구해집니다.
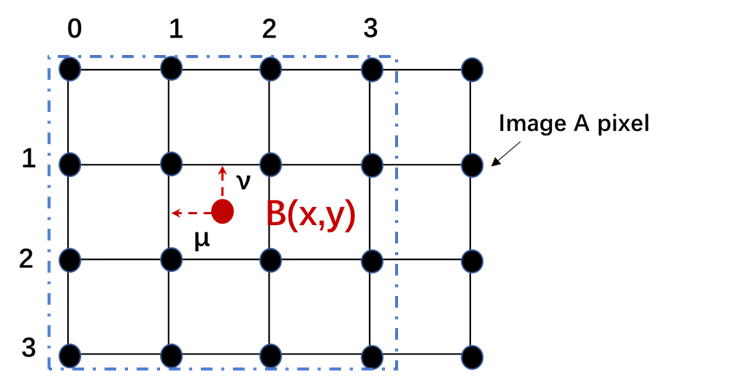
Bicubic Interpolation도 위의 그림을 통해 상상해봅시다.
어쨌든 Interpolation의 방법이 SR의 Solution이 된다는 것입니다. Input Image과 Output Image의 차이를 생각해보거나 Upsampling, Downsampling을 배울 때 Interpolation에 대한 이해는 많은 도움이 될 것입니다.
