이번 포스팅은 standford university의 cs231 lecture 5를 공부하고, 강의와 슬라이드를 바탕으로 정리한 글임을 밝힙니다.
Reference
💻 유튜브 강의: Lecture 5 | Convolutional Neural Networks
💻 한글 강의: cs231n 7강 CNN
📑 slide: PDF
📔 1. CNN 개요
📔 2. Why CNN?
📔 3. CNN의 구조
📗 Intuitively Understanding Convolutions for Deep Learning
📕 06. 합성곱 신경망 - Convolutional Neural Networks
Contents
cs231 내용을 정리할 때, 주로 강의 내용만을 바탕으로 정리하였습니다. 하지만 강의 내용만으로는 부족하다 판단했고, CNN에 대한 좋은 자료가 더 많아서 함께 짬뽕으로 정리하려고 합니다.
그래도 cs231에서 나오는 내용을 바탕으로 관련된 개념만 다루려고 합니다.
강의 내용에만 집중하고 싶으시다면 다른 포스팅도 추천 드립니다.
Outline
Multi-layered Neural Network
Convolutional Neural Networks은
합성곱 신경망이라 부르며, 흔히CNN이라 줄여 부릅니다.
Neural Network을 통해 학습하여 해결하기 어려웠던 문제들을 해결할 수 있었습니다.
다만, 영상 기반 인식 알고리즘에서 좋은 결과를 얻으려면, 사전에 많은 처리 과정이 필요했습니다.
기존 multi-layered neural network를 영상에 바로 적용하는 것은 어려웠습니다.
multi-layered neural network가 갖고 있는 문제점은 무엇이었을까요?
이상적인 머신 러닝 시스템은 training data만 적절히 많이 넣어주면 알아서 분류까지 해주는 것(unsupervised learning)을 기대했지만, 그렇진 않았습니다.
대안으로 prior knowledge를 이용해 네트워크의 구조를 특수한 형태로 변형 시켜줍니다.
2D 이미지가 갖는 특성을 최대한 살릴 수 있는 방법으로 무엇이 있을까요?
아래 예시를 통해 살펴보겠습니다.
multi-layered neural network를 이용해서 32*32 size를 갖는 숫자 필기체를 인식하는 경우를 살펴보겠습니다.
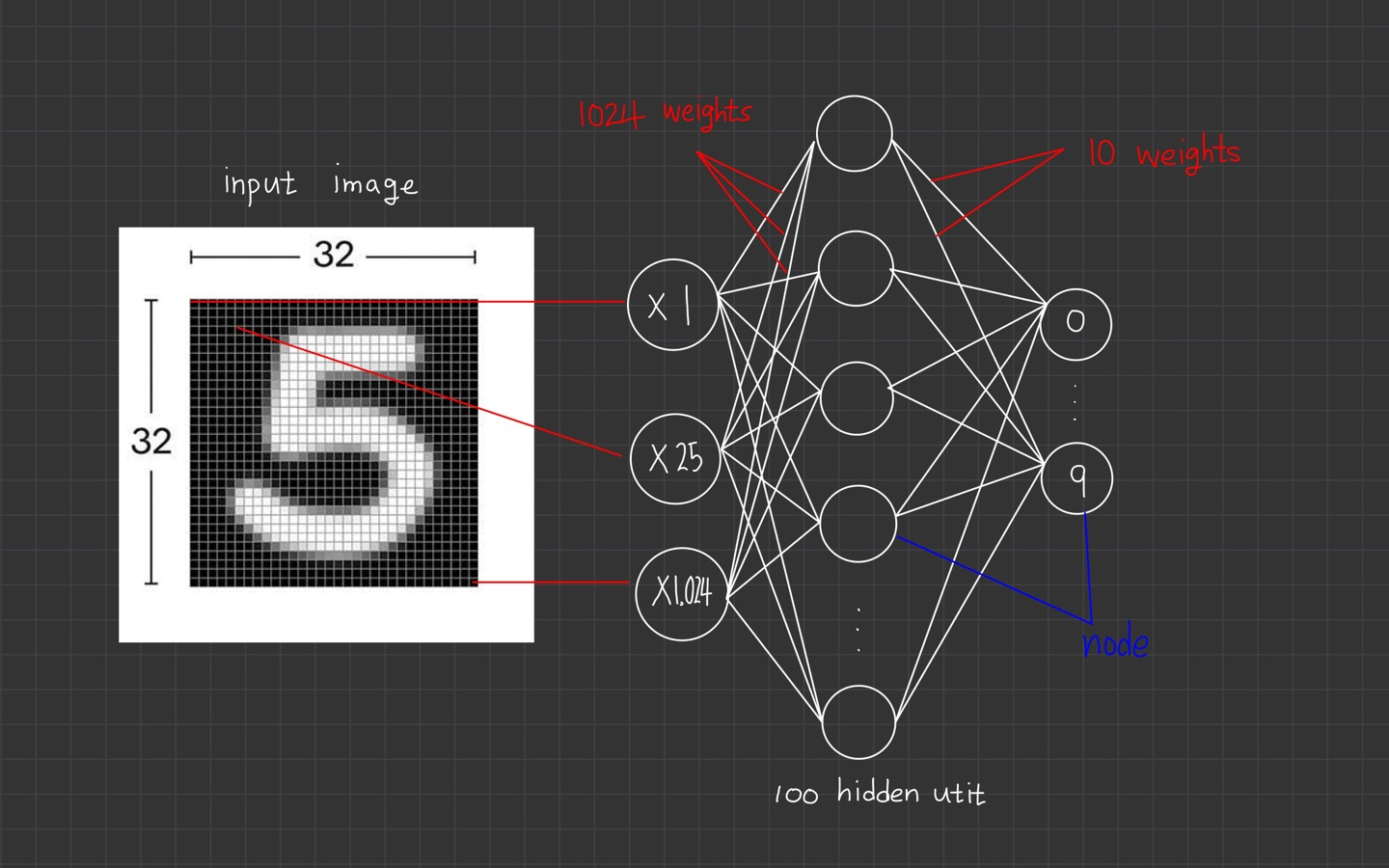
- input image: 32*32 size
- 1 hidden layer
- 100 units
- 10 output
필기체 인식을 위해 위 그림처럼 32*32 size의 pixel을 펼쳐둔 1024개의 입력이 있고, 100개의 node가 있는 hidden -layer 및 10개의 output layer로 구성되어 있습니다.
input data가 1차원 배열로 바꿔주는 과정에서 문제점이 생깁니다.
바로 데이터의 형상이 무시된다는 점입니다.
Image Data의 경우 세로, 가로, 채널의 3차원 형상을 갖고 있습니다. 이 형상을 공간적 구조(spatial structure)을 가진다고 말합니다.
공간적 구조를 갖고 있는 형상의 예를 들어 보겠습니다.
- 공간적으로 가까운 픽셀은 값이 비슷합니다.
- RGB의 각 채널끼리 서로 밀접하게 관련되어 있습니다.
- 거리가 먼 픽셀끼리는 관련이 없습니다.
등 3차원 공간에서는 정보가 내포되어 있게 됩니다.
하지만 FC-layer(Fully Connected Layer)에서는 1차원의 vector로 변환되며 정보들이 사라집니다.
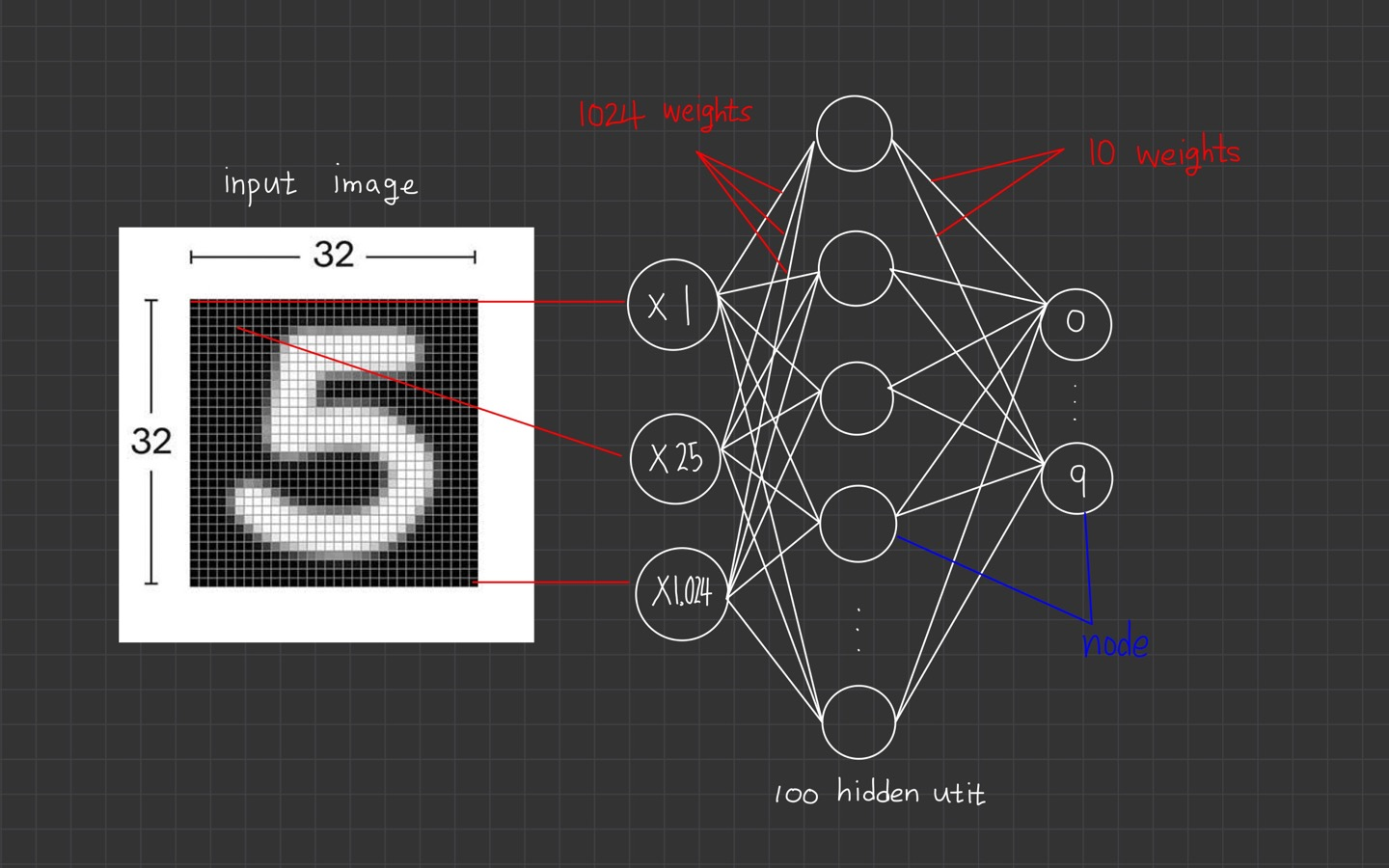
다시 해당 그림을 살펴보겠습니다.
위 그림의 구조는 hidden layer가 1개만 있는 단순한 구조입니다.
여기서 필요한 가중치(weight)와 편향(bias)는 몇 개일까요?
1024 * 100 + 100 + 1000 + 10 = 103,510
여기서 필요한 weight과 bias는 총 103,510개입니다. input data가 커지거나 hidden layer가 2단 이상일 경우 parameter 개수가 엄청나게 많아집니다.
이렇게 많은 parameter를 어떻게 처리해야 할까요?
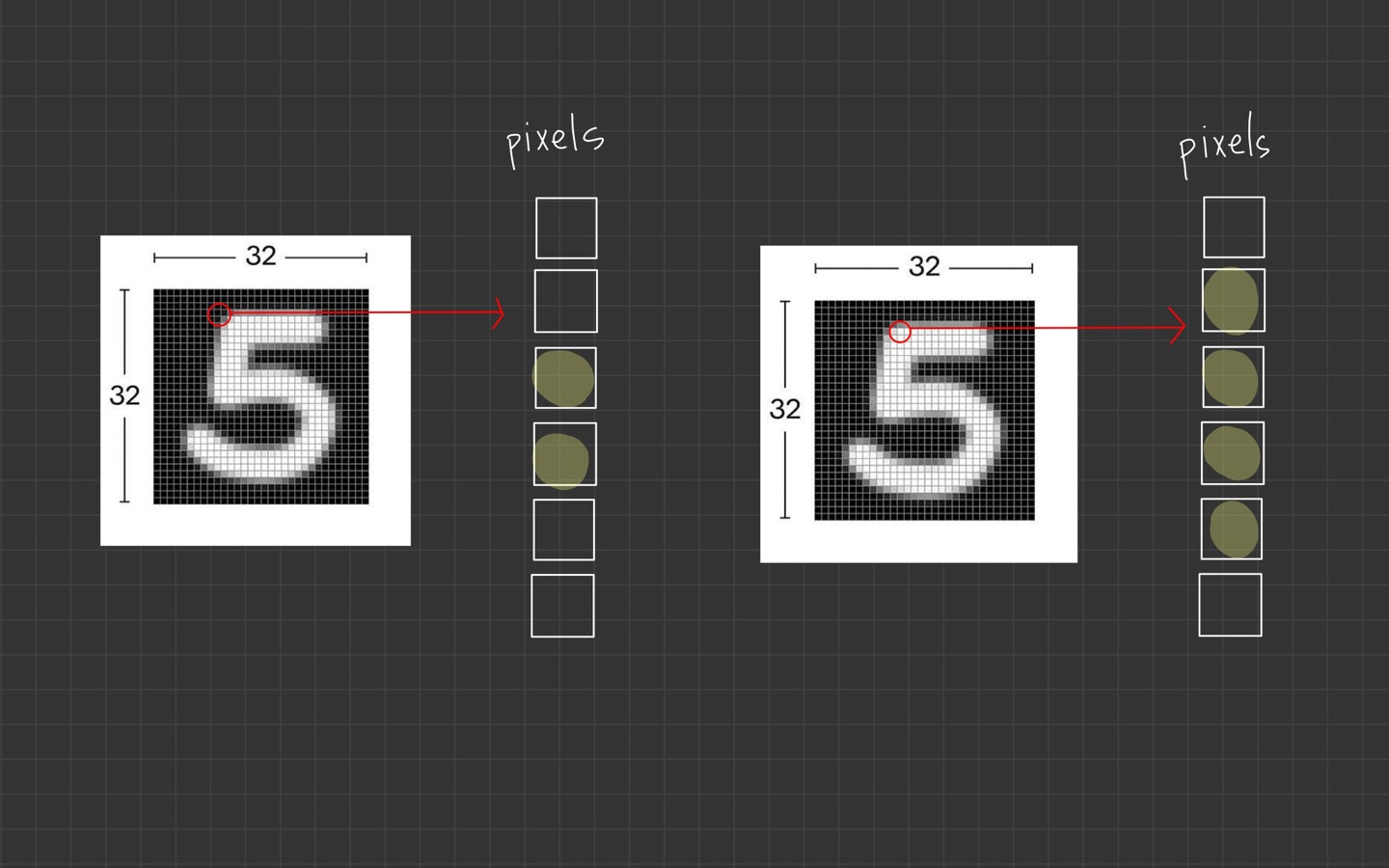
기존 neural network는 전체 글자에서 2픽셀 값만 달라져도 새로운 학습 데이터로 인식하고 처리합니다.

글자의 크기가 달라지거나 회전되는 등 작은 변형(distortion)이 조금만 생겨도 이러한 데이터를 모두 새로운 데이터라 인식합니다.
그래서 모든 변형을 반영한 데이터를 넣어주는 것이 아니라면 좋은 결과를 기대하긴 어렵습니다. 사실상 불가능에 가깝죠.
이는 기존 multi-layered neural network가 갖고 있는 한계점입니다.
문제점
글자의 topology를 고려하지 못하고 pixel로 입력 받는 raw data에 대해 직접 처리를 하기 때문에 많은 training data가 필요로 하고, 학습 시간도 오래 걸립니다.
위의 예시를 Gray-scale에 적용한다면 개의 패턴이 나오므로 전처리 과정 없이는 불가능합니다.
기존 FC-layer neural network를 사용하면 3가지 문제점이 발생합니다.
- Training time
- Network size
- Number of free parameter
MLP를 vision에 적용할 때 나타나는 이러한 문제점을 해결하기 위해 CNN이 나오게 되었습니다.
MLP는 모든 입력이 위치와 상관없이 동일한 수준의 중요도를 갖습니다. 그래서 parameter의 크기가 상당히 커지는 문제가 발생했고, visual cortex와 유사한 신경망을 만들고 싶었습니다.
결과적으로 CNN(Convolutional Neural Network)이 나오게 되었습니다.
Why CNN?
Receptive Field
Receptive Field란 생명 과학 영역에서는 수용 영역이라 부릅니다.
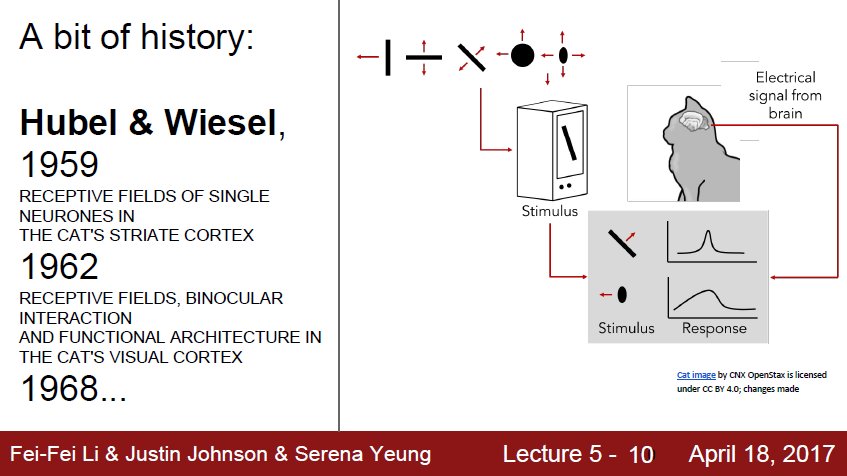
David H. Huble과 Torsten Wiesel은 1958년과 1950년에 시각 피질의 구조에 대한 고양이 실험을 수행했습니다. 이 고양이 실험이 주는 결과가 매우 중요합니다.
실험을 통해 시각 피질 안의 많은 뉴런이 Local Receptive field를 가진다는 것을 알게 되었습니다.

뉴런들이 시야의 일부 범위 안에 있는 시각 자극에만 반응하였습니다.
뉴런의 수용 영역(Receptive Field)들은 서로 겹칠 수 있고 겹쳐지는 수용 영역들이 전체 시야를 이루게 되는 것입니다.
어떤 뉴런은 수직선의 이미지에만 반응하고, 어떤 뉴런은 각도가 바뀔 때마다 선에 반응하였고, 어떤 뉴런은 저수준의 pattern(edge, blob 등)이 조합되어 복잡한 패턴(texture, object)에 반응한다는 것을 알게 되었습니다.
이러한 관찰을 통해 고수준의 뉴런이 이웃해 있는 저수준의 뉴런의 출력에 기반한다는 아이디어를 생각해냈습니다.
cs231에서도 해당 내용이 소개되고 있습니다.
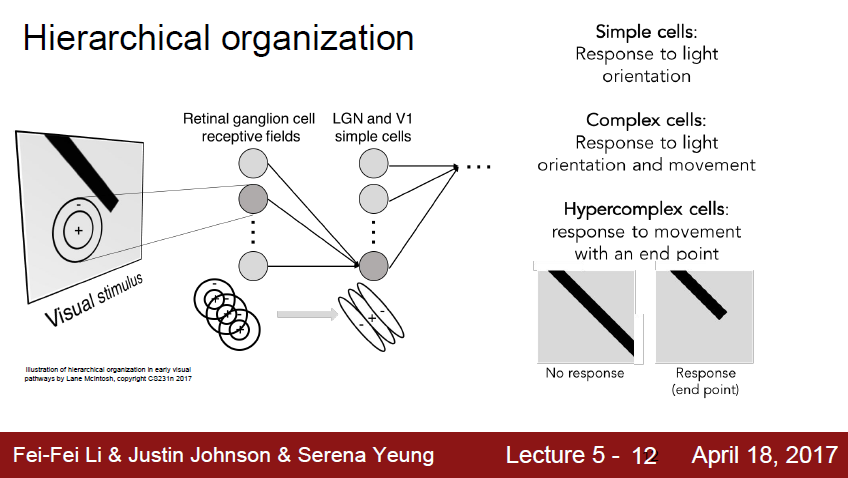
뉴런은 위 이미지처럼 계층구조를 가집니다.
다양한 종류의 시각 자극을 관찰하여 시각 신호를 전달 받습니다.
오른쪽 가장 상위에 있는 simple cells이 다양한 edges의 빛의 방향에 반응합니다. complex celss는 방향과 빛에 반응합니다.
복잡도가 더 증가함에 따라 Hypercomplex cells은 끝점에 더 반응하게 됩니다.
해당 아이디어가 바로 합성곱 신경망(CNN, Convolution Neural Network)으로 진화되었고, 1998년 Yann Lece et al.의 논문에서 손글씨 숫자를 인식하는데 LeNEt-5가 소개되며 CNN이 등장하였습니다.
FC-layer와는 달리 CNN은 Convolutional layer와 pooling layer로 구성되어 있습니다.
Convolution
Convolution을 처음 공부하게 될 때 커널(kernel), 필터(filter), 채널(channel) 등과 같은 용어로 혼란스러울 수 있습니다.
합성곱 신경망(convolution Neural Network, CNN) 에서는 Fully-Connected(Dense) Neural Network와 달리 Neuran을 필터(filter) 혹은 커널(kernel)이라 부릅니다.
뉴런(neuran) = 필터(filter) = 커널(kernal)
다 같은 용어지만, 부를 때 살짝 차이가 있다면
커널(kernal): 입력에 곱하는 가중치
필터(filter): 뉴런의 개수
해당 의미로 주로 사용한다고 합니다. 하지만 막상 공부해보니 다 혼용되며 사용되고 있더군요. 그래서 헷갈리지 않게 잘 이해하며 넘어가는 것이 가장 중요하다 생각합니다.
하나씩 살펴보겠습니다.
영상 처리 분야에서 convolution은 주로 filter 연산에 사용됩니다. 영상들로부터 특정 feature들을 추출하기 위한 필터를 구현할 때 convolution을 이용합니다.
2D Convolution으로 살펴보겠습니다. Kernel은 weight의 작은 행렬을 의미합니다. 이 kernel은 2D input data를 ‘슬라이딩(sliding)’하면서 요소별 곱(elementwise multiplication)을 수행하고, 결과를 a single output pixel로 합산합니다.
아래 이미지를 통해 살펴 보기를 바랍니다.
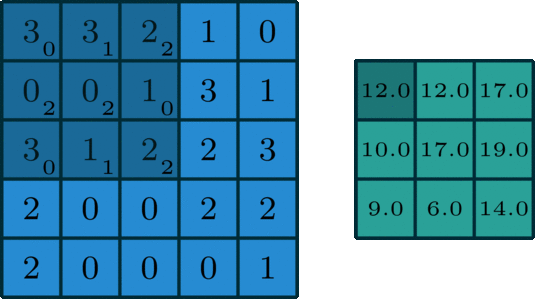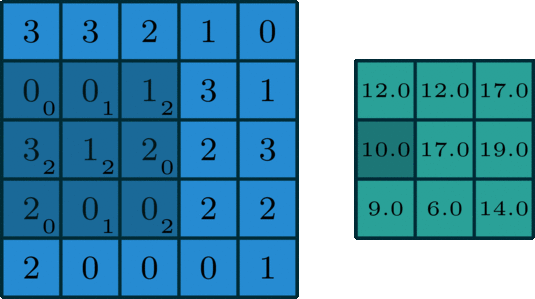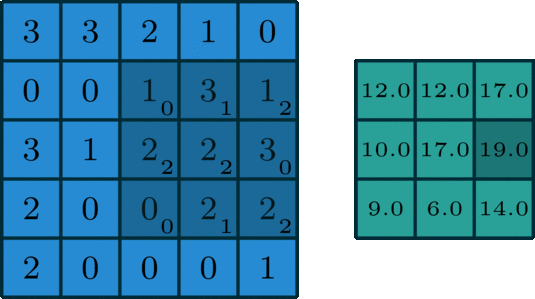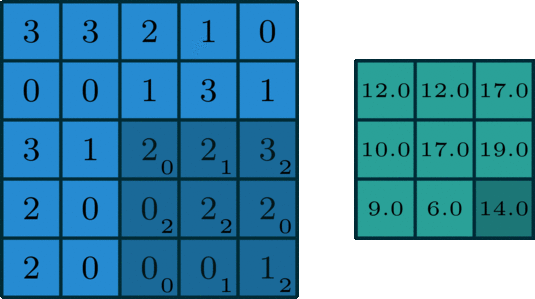
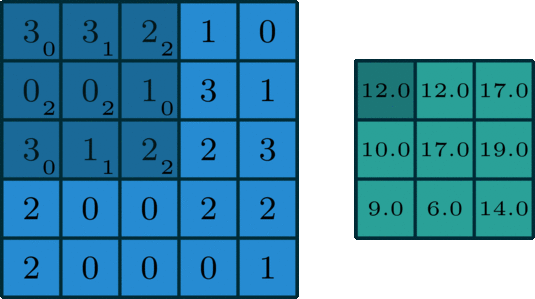
예시로 의 결과를 얻을 수 있습니다.
여기서 용어를 다시 정리하고 가면,

size로 돌아다니며 곱해지는 숫자들이 kernel을 의미합니다. 그래고 곱해져서 연산이 수행되면 결과로

해당 값이 나오게 되는 것입니다. 그리고 오른쪽으로 아래로 한 칸씩 이동하고 있는데 이 경우를 stride는 1이다라고 얘기합니다.
kernel은 모든 위치를 돌아다니며 해당 과정을 반복합니다.
그리고 2D matrix of features를 2D matrix of features로 변환합니다.
2D matrix of features -> 2D matrix of features
output feature은 input layer의 output feature과 거의 동일한 위치에 있는 input feature들의 가중합(weighted sum)이 됩니다.
gif에서 보이는 kernel의 이동을 보시면 해당 설명이 이해가 될 거라 생각합니다.
이건 FC-layer와는 비교되는 부분입니다. 위의 예시는 5x5=25개의 input feature와 3x3=9개의 output feature을 갖고 있습니다.
FC-layer라면 25x9=225 parameter의 weight matrix를 갖게 되며, 모든 output feature은 모든 single input feature의 가중합이 됩니다.
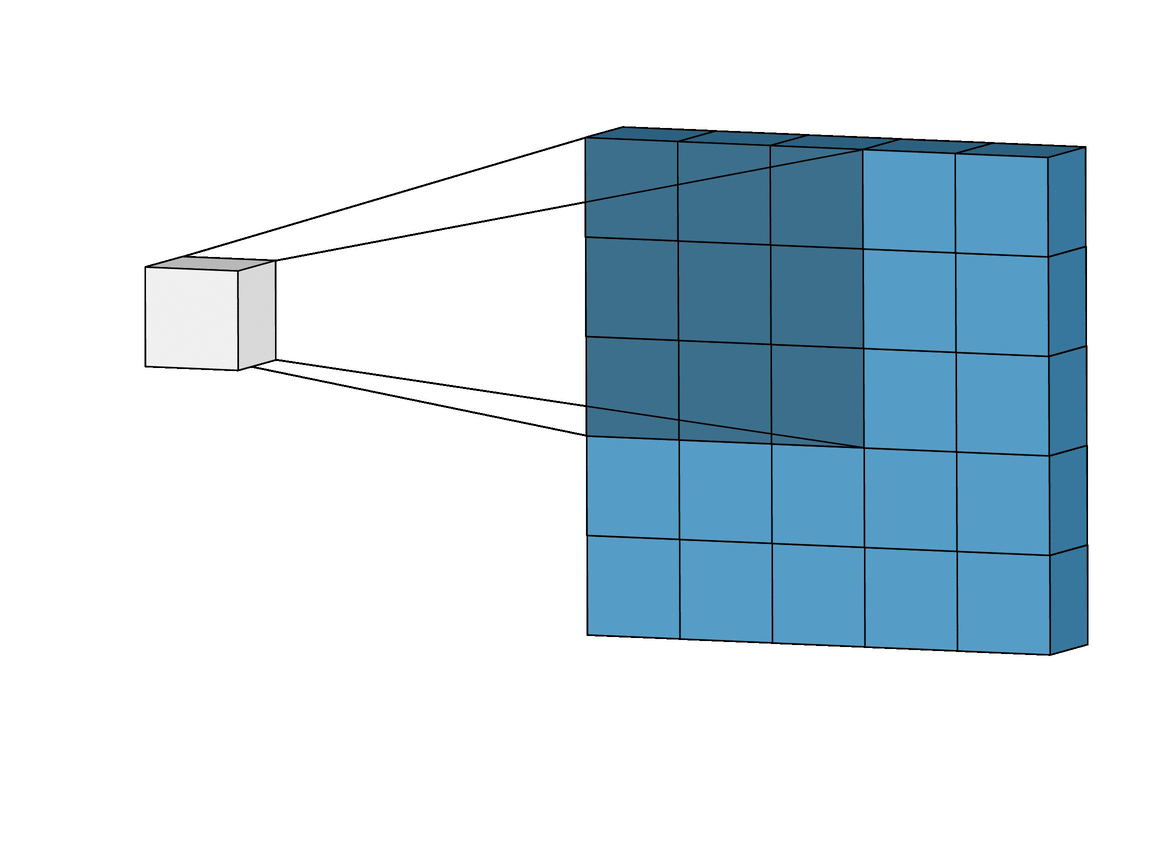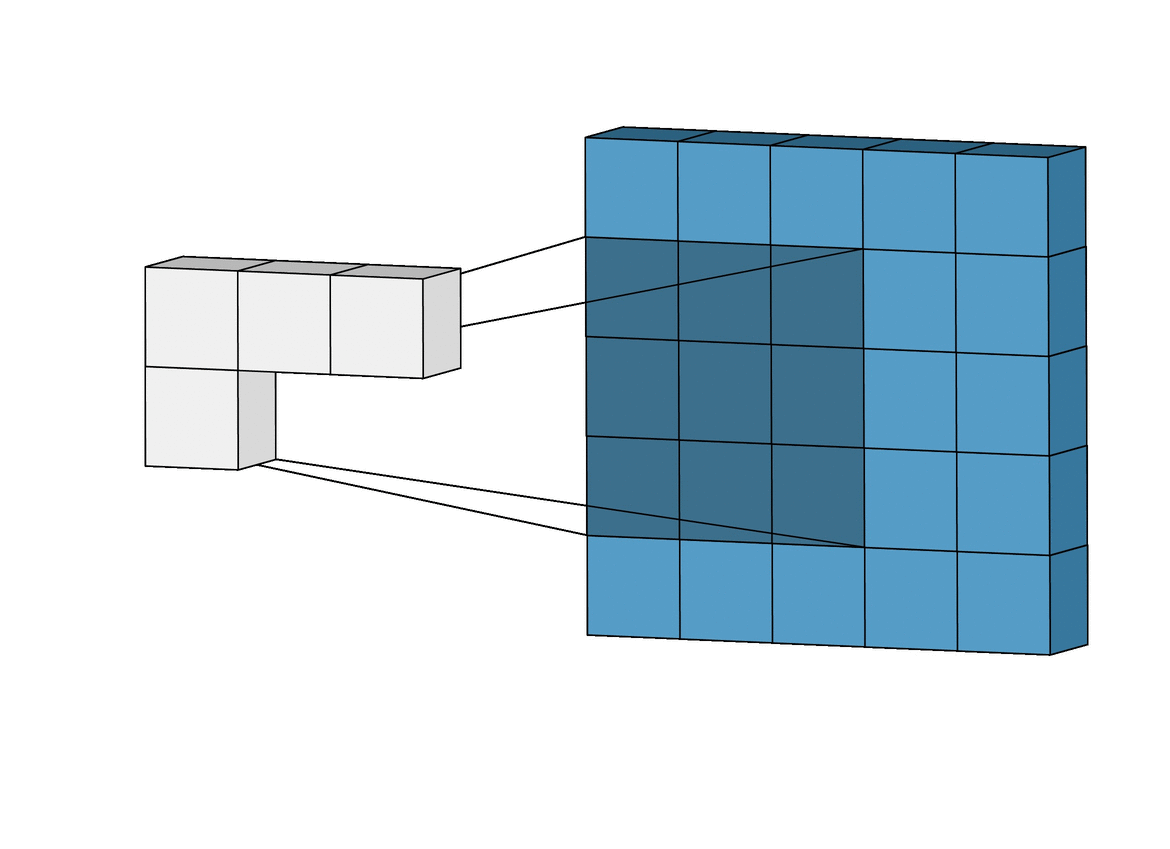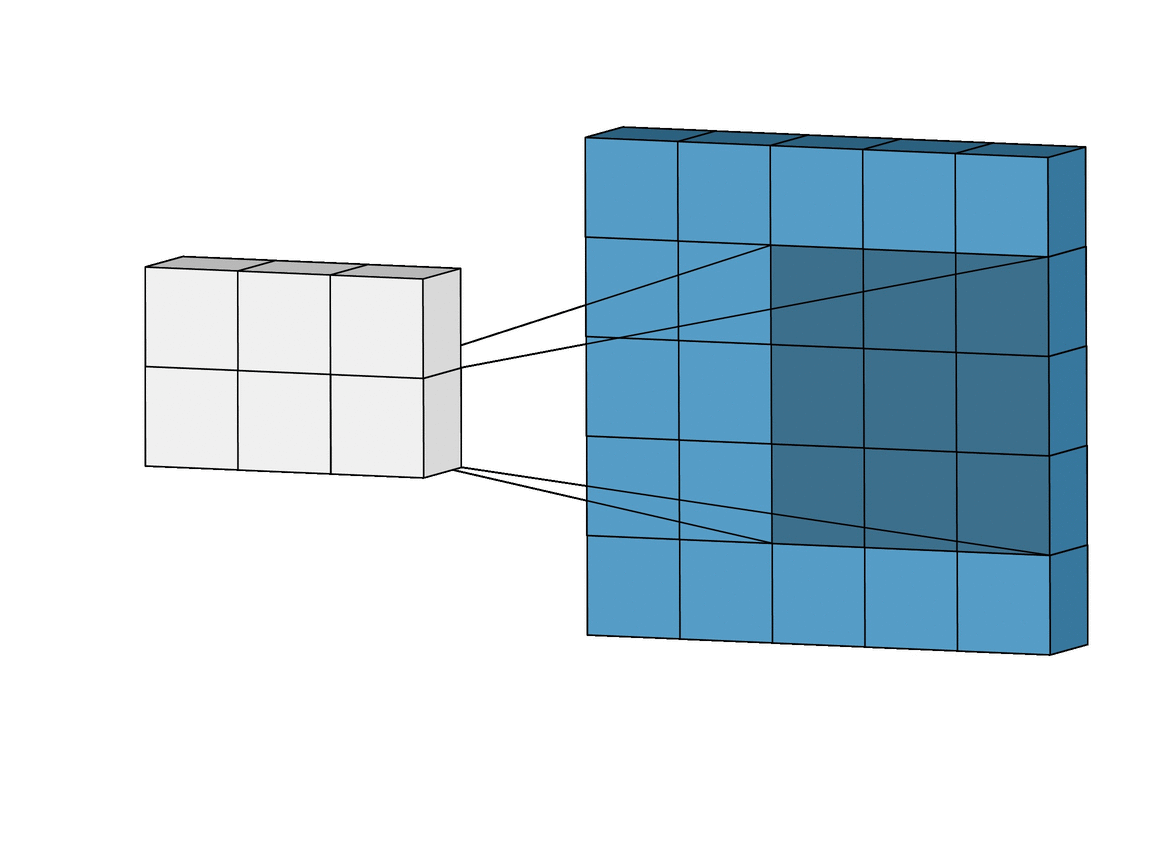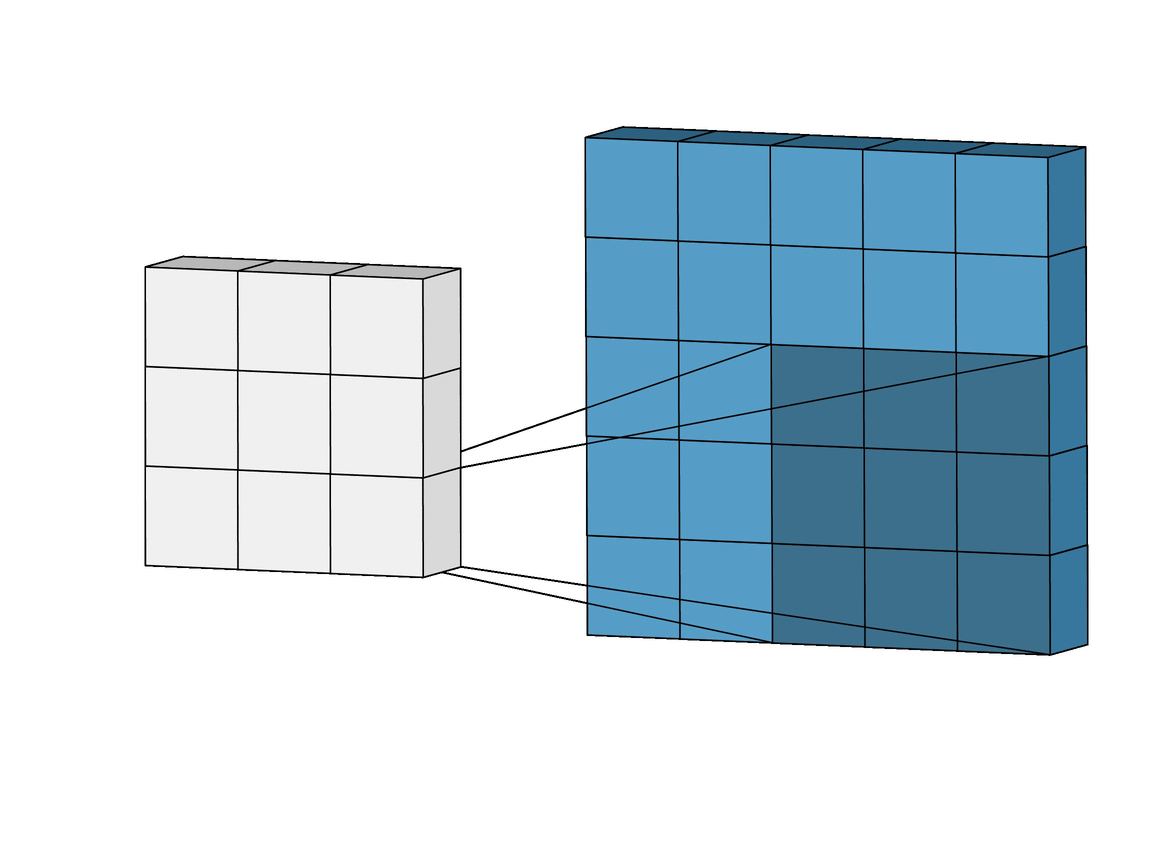
Convolutional Layer에서는 위의 그림처럼 입력 이미지의 모든 픽셀 정보와 연결되는 것이 아닌, kernel이 닫는 Receptive Field 안의 픽셀끼리만 연결이 되어서 앞의 Conv Layer(Convolutional Layer)에는 low-level feature에만 집중하고, 뒤로 갈수록 high-level feature에 집중합니다.
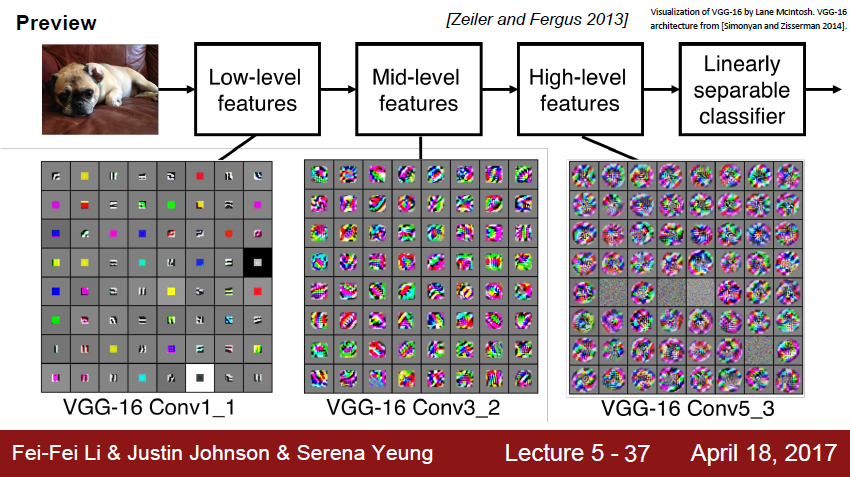
위 슬라이드는 VGG-16의 모델을 사용하였습니다. 첫 번째 layer의 filter를 visualize한 이미지입니다.
edge나 color를 표현한 blob이 통합된 상태입니다. 점점 갈수록 잡아내는 특징이 고수준으로 높아지고 있는 것을 확인할 수 있습니다.
CNN 특징
Neural Network 앞에 Convolution이 붙어 CNN이라 줄여 부르는데요.
Convolution의 특성을 살린 신경망 연산을 한다는 의미입니다. 기존 multi-layered neural network에 비해 중요한 특징을 갖습니다.
- Locality(Local Connectivity)
앞에서 얘기한 내용을 정리해보겠습니다.
- kernel이 작은 local 영역의 픽셀만 결합하여 output을 만들었습니다.
- 즉, output feature은 작은 local area에서 input feature만 보는 역할입니다. - kernel은 output matrix를 만들기 위해 이미지 전체에 적용됩니다.
픽셀은 항상 일관된 순서를 가지며, 서로 인접한 픽셀끼리 영향을 줍니다. 만약 모든 근처의 픽셀이 빨간색이라면 해당 픽셀도 빨간색일 가능성이 높습니다.
이렇게 픽셀은 주변 픽셀 값과 비교하여 정보를 추측할 수 있습니다. 이런 특성을 locality라고 합니다.
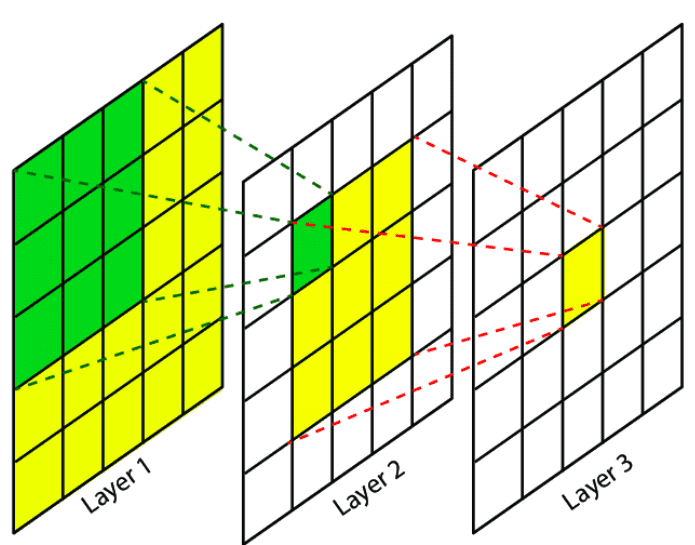
CNN은 Receptive Field와 유사하게 local 정보를 이용합니다. filter를 여러 개 적용하면 다양한 local 특징을 추출해내는데요.
input data에 filter를 적용해서 feature map을 출력하여 다음 layer로 전달합니다.
여기서 Subsampling 과정을 거치면서 영상의 크기를 줄이고, local feature들에 대한 filter 연산을 반복하여 global feature을 얻습니다.
- Shared Weights
Conv의 개념을 설명할 때 봤던 이미지를 살펴보면, 동일한 계수를 갖는 filter를 전체 영상에 반복적으로 이용합니다.
변수의 수를 줄일 수 있으며, topology 변화에 무관한 invariance를 얻게 됩니다.
CS231 Lecture 5
Review
이전 강의에서 Fully Connected Layer에 대해 배웠습니다.
32323 image가 있는 경우, 1차원 vector로 표현하면 3072*1 size로 변합니다.
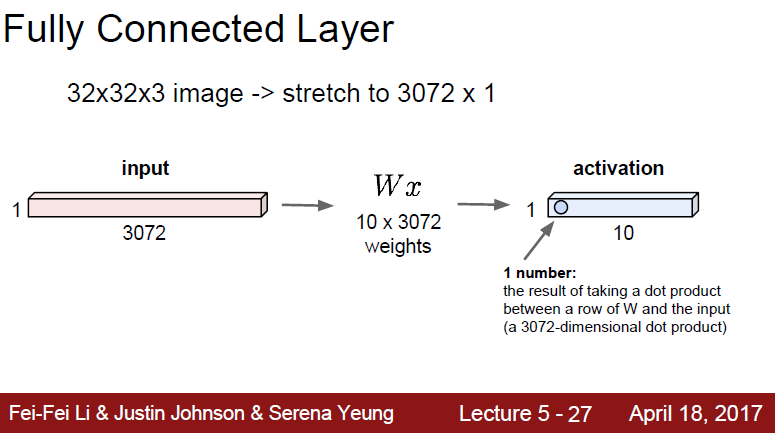
그리고 가중치 행렬과 곱해져서
X
의 activation이 만들어집니다.
여기까지가 이전 강의에서 다뤄왔던 내용입니다.
Convolution Layer(합성곱 층)

xx의 spatial structure을 가진 image가 있습니다.

여기에 xx filter로 Convole 해줍니다.
해당 슬라이드에 중요한게 적혀 있습니다.
- Filters always extend the full
depth of the input volume.
filter는 항상 입력의 채널의 수만큼 확장이 되어야 한다는 뜻입니다.
3 channel을 가진 image의 filter도 똑같은 3 depth을 가집니다.
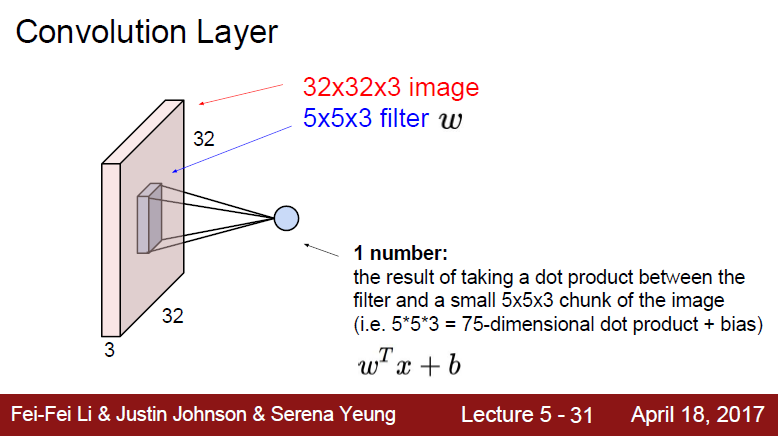
여기서 식이 로 표시된 이유는 행렬 곱을 해주기 위해서입니다. 가중치 행렬을 전치하여 input data 와 곱해줍니다. 그 다음에 편향 를 더해줍니다.
슬라이드 적혀 있는 내용입니다.
- the result of taking a dot product between the filter and a small 5x5x3 chunk of the image (i.e. 5x5x3 = 75-dimensional dot product + bias)
결과는 image의 작은 5x5x3 chunk와 filter 사이의 dot product를 통해 계산됩니다. (5x5x3으로 75-dimensional의 dot product + bias 가 됩니다)
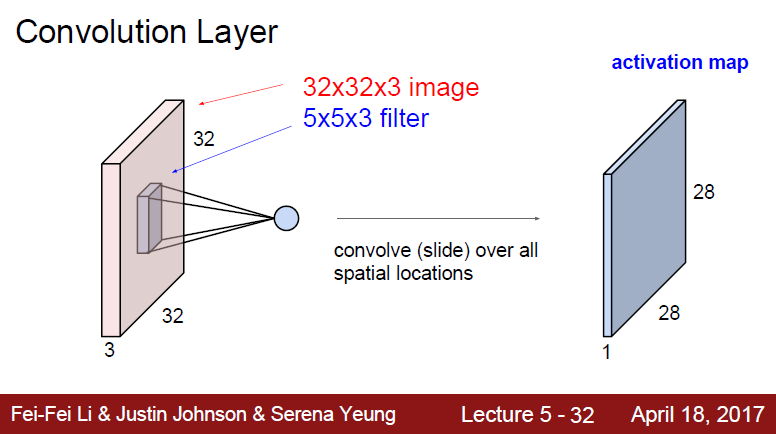
그래서 28x28x1 크기의 activation map이 나오게 됩니다. 여기서는 filter가 1개라고 가정했습니다.

이번 슬라이드에서는 filter가 6개라고 가정을 했고, 28x28x1 size인 총 6개의 activation map이 생겨
28x28x6 size activation map이 생겼습니다.
Conv Layer의 input data를 filter가 sliding하며 Convolve하여 만든 출력을 feature map이라 합니다.(또는 Activation Map이라고 합니다.)
거의 같은 의미로 쓰이는 것 같은데 feature map과 activation map의 차이가 있는지 궁금해서 찾아보았는데요.
Feature Map은 Convolution 연산으로 만들어진 Matrix입니다.Activation Map은 Feature Map Matrix에 activation function을 적용한 결과입니다.
즉, Conv layer의 최종 output이 activation Map입니다.
생각해보면 이름에서 차이를 알 수 있었는데 말이죠.😑
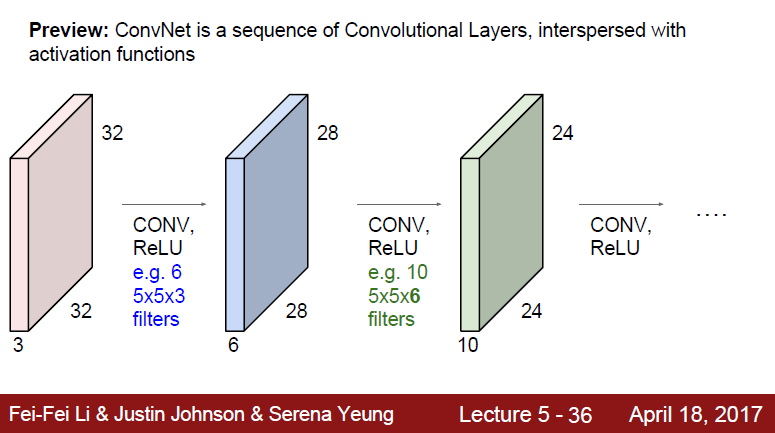
이제 계속 Conv layer를 통과시켜보겠습니다.
-
32x32x3 size에 6개의 5x5x3의 filter를 지나 28x28x6 size의 activation map이 만들어짐
-
28x28x6 size에 10개의 5x5x6 filter를 지나 24x24x10 size의 activation map이 만들어짐
이런식으로 연산이 됩니다.
슬라이드 41p부터 55p까지는 Conv layer를 통과한 input data가 어떤 size로 변하는지 예시를 보여주고, padding과 stride에 대한 개념을 설명합니다.
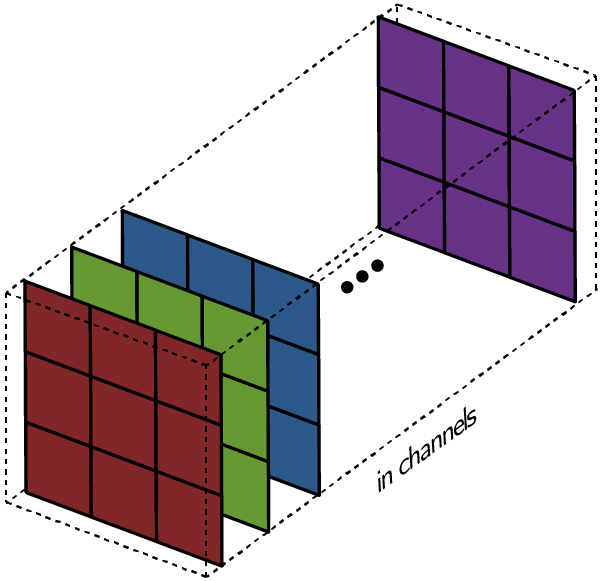
*A filter: A collection of kernels
Padding(패딩)
Padding(패딩)은 Conv 연산을 수행하기 전, 입력 데이터 주변을 특정 값으로 채워서 늘리는 것을 의미합니다.
쉽게 말하면 가짜 픽셀을 가장 자리에 넣어주는 것입니다.
Padding은 출력 데이터의 Spatial Structure을 조절하기 위해 사용합니다.
Padding할 때 채울 값은 지정해줘야 하는 hyper-parameter에 속합니다.
그래서 해당 값을 0으로 채우는 경우를 zero padding이라고 합니다.
Spatial Structure을 조절하기 위해 굳이 Padding을 사용하는 이유는 무엇일까요?
가장 큰 문제점은 가장 자리의 주요한 정보를 놓칠 수도 있기 때문입니다.
kernel이 sliding하며 주요 feature를 뽑아 activation map을 만드는데, 가장 자리는 kernel이 많이 닿을 수가 없습니다.
반대로 중앙부의 data는 정보를 많이 반영할 수 있겠죠.
이렇게 반영되는 정보의 차이를 줄이기 위해 생긴 것이 Padding입니다.
또한, 아까 위 예시에서 봤듯이 data는 Conv layer를 지날 때마다 지속적으로 작아집니다...
32x32x3 -> 28x28x6 -> 24x24x10
주로 Conv layer의 output이 input data의 Spatial Structure와 동일하게 맞추기 위해 사용합니다.
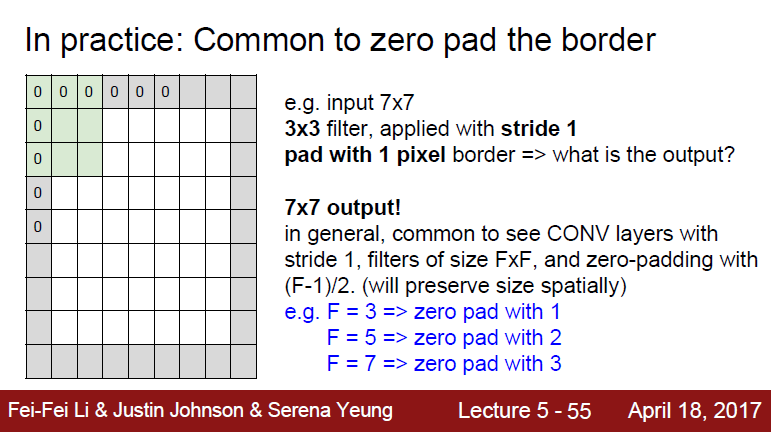
해당 슬라이드는 제로 패딩을 하고, stride 1을 했을 경우 output size를 계산하고 있습니다.
Stride(스트라이드)
Stride는 앞에서 살짝 언급했습니다.
input data에 filter를 적용할 때 이동 간격을 조절해주는 매개변수입니다.
즉, 얼마큼씩 이동할 것인가? 이동 간격을 의미합니다.
stride 또한 output data의 size를 조절하기 위해 사용되는데요.
보통 1과 같이 작은 값에서 더 잘 작동하며, stride가 1인 경우 input data의 Spatial Structure는 pooling layer에서만 조절할 수 있게 됩니다.
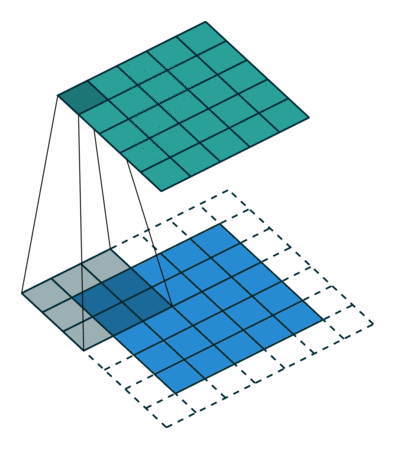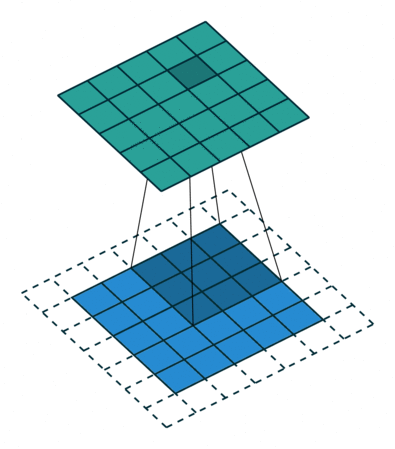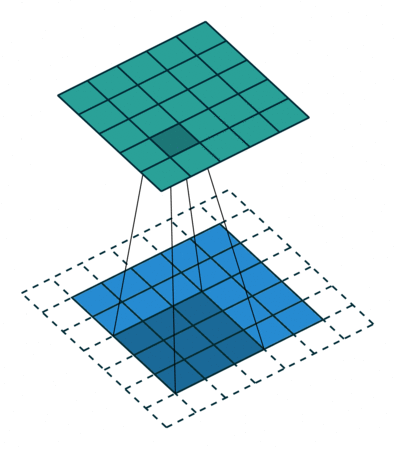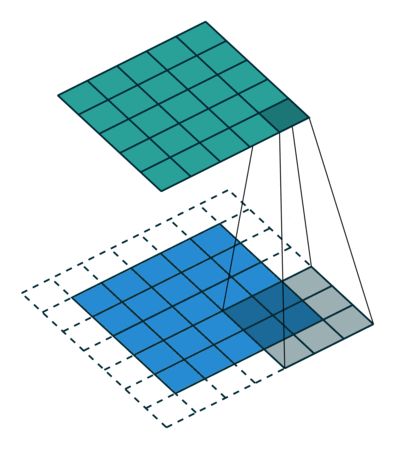
padding 후 3x3 size kernel로 convolve 한 후 5x5 size의 feature map이 나온 것을 볼 수 있습니다.
가장 자리의 pixel은 kernel의 중심에 절대 닿을 수 없습니다.
kernel은 edge 부분을 넘어 확장할 수 없기 때문입니다.

여기서도 3x3 filter는 7x7 input data의 spatial을 넘어버리기 때문에 불가능하다고 나옵니다.
Output size
output size를 계산하는 식이 나옵니다.
Padding과 Stride를 적용하고, input data와 filter의 크기가 주어졌을 때 output data의 크기를 구할 수 있습니다.

위의 경우는 input data의 size가 NxN으로 행렬 사이즈가 같은 경우입니다.
하지만 사이즈가 달라도 결국 계산식은 같습니다.
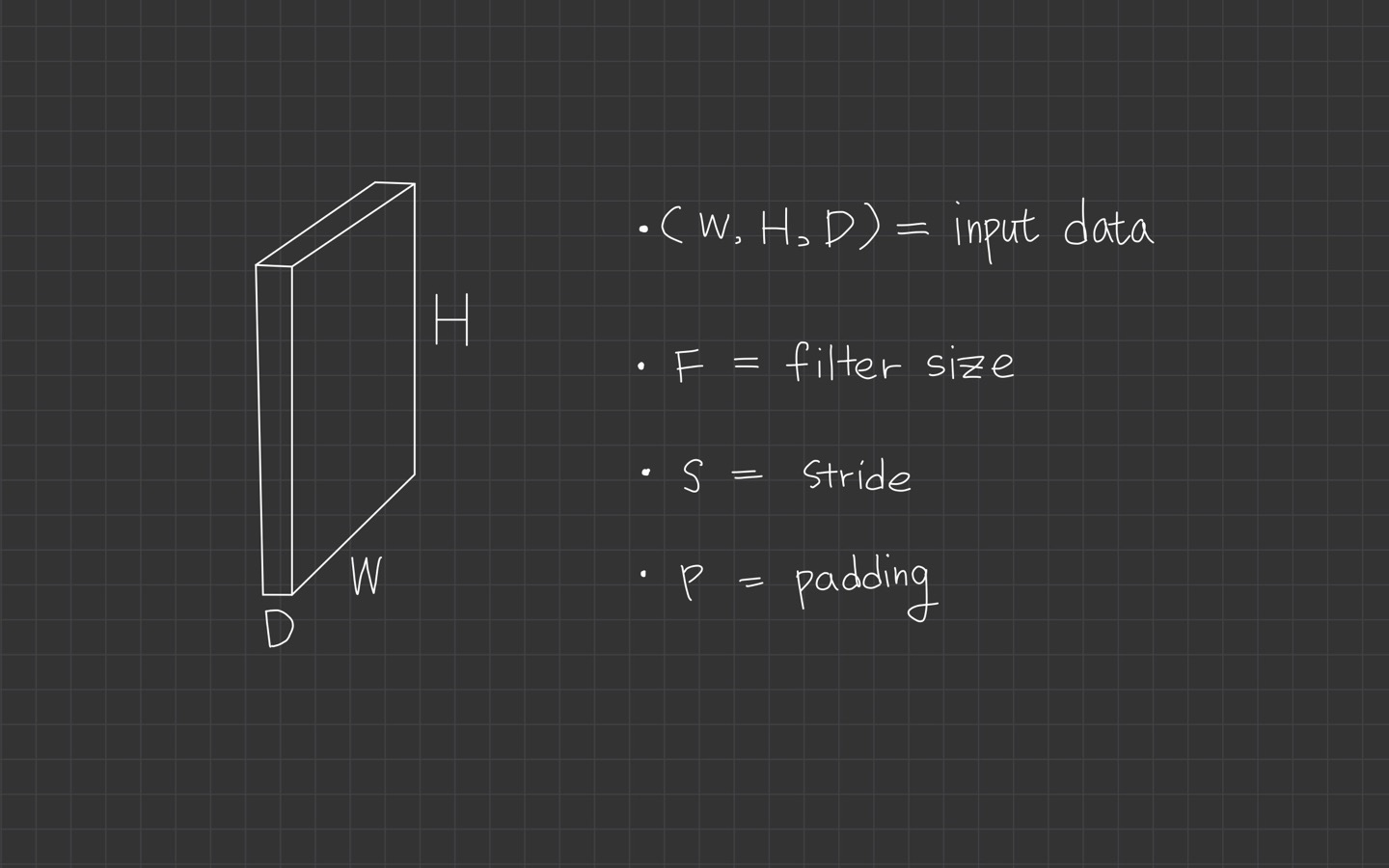
계산식은 이렇습니다.
행과 열이 size가 다른 경우 해당 식을 참고하시면 될 것 같습니다.
depth는 filter의 개수 K와 같습니다.
슬라이드로는

p62에 나오는데, 해당 슬라이드를 몇 번 재탕했는지 화질이 좋진 않네요.
Reminder
마지막 개념 pooling으로 넘어가기잔 Conv layer의 특징에 대해 정리하고 갑니다.
아까 위에서 말한 CNN 특징과 똑같은 내용입니다.
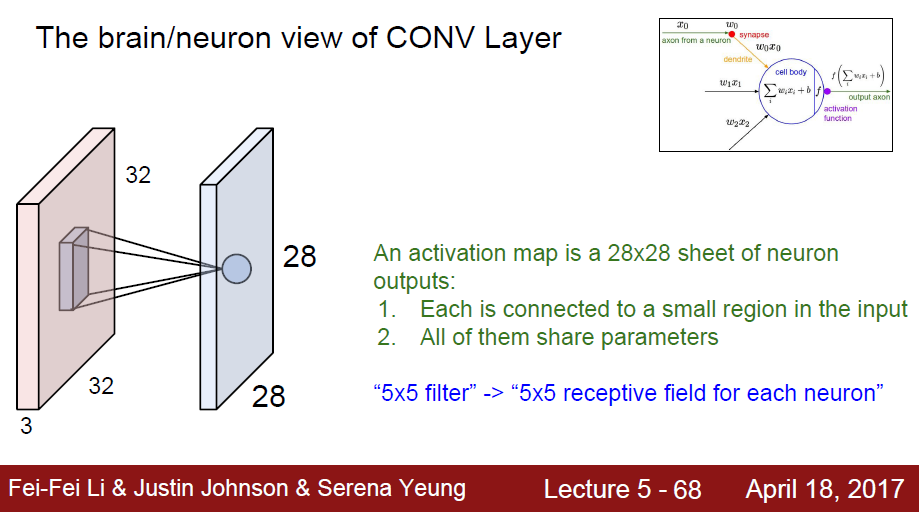
28x28 size의 activation map는
- input data에서 작은 영역에서 나온 각각의 값이 모두 연결된 것입니다. (dot product를 통한 1 number의 모음)
- 모두 같은 parameter를 공유한다. kernel의 값을 공유합니다.
- 5x5 filter란? 각 뉴런에 대한 5x5 receptive field(수용 영역)이다.
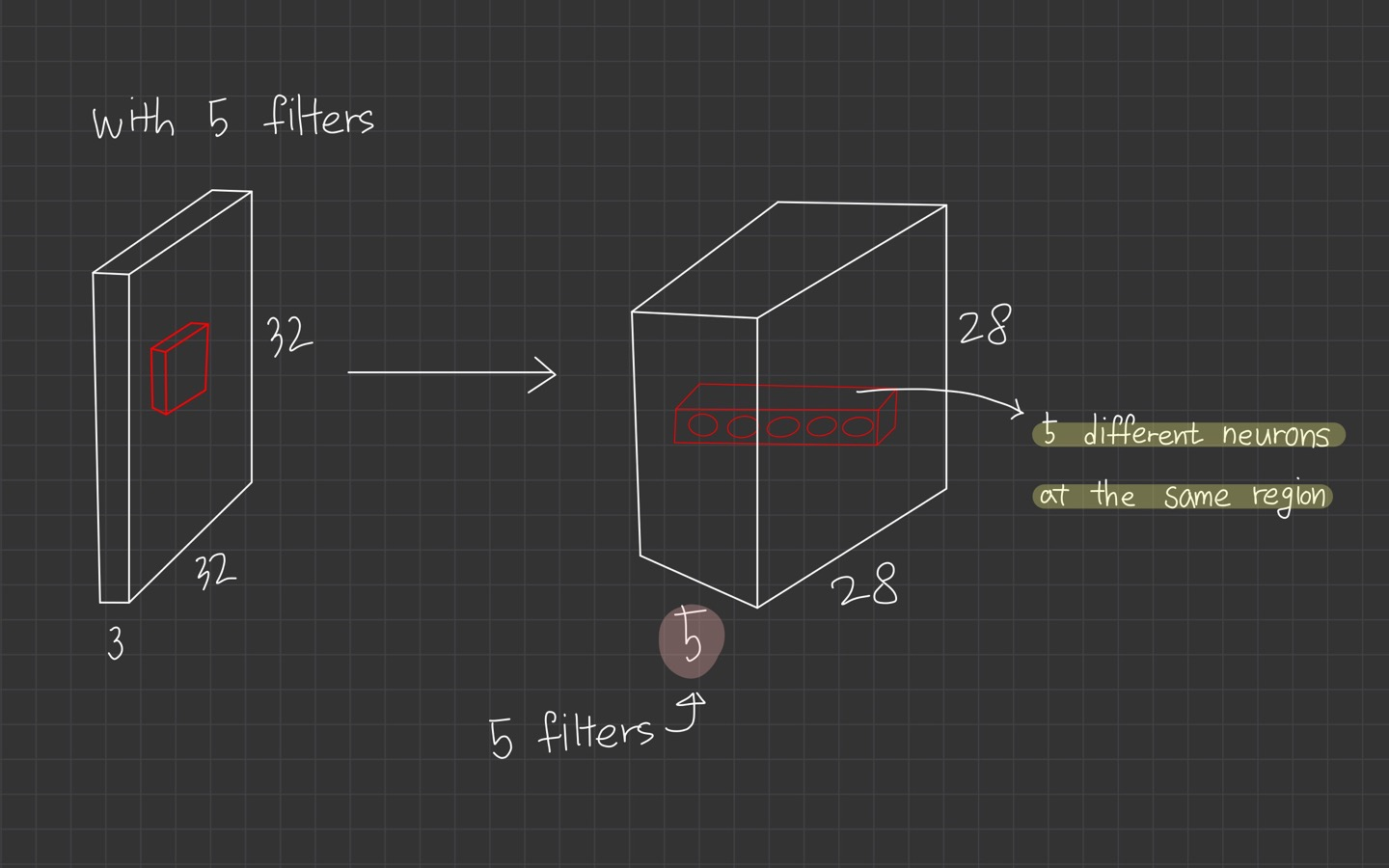
복습
- 5개의 filter를 사용했으므로 activation map의 depth가 5이다.
- 5개의 filter를 사용했으므로 같은 same region에서 5개의 다른 neuron 값이 나온다.
- filter size가 결국 각 뉴런에 대한 receptive field이다.
Pooling
CNN architecture에는 Pooling layer가 꼭 들어갑니다.
input data의 size가 network 시작부터 끝까지 점점 작아집니다. 반면 channel의 수는 점점 깊어집니다.
이것은 stride와 pooling을 통해 수행됩니다.
Locality는 output이 볼 이전 layer의 input을 결정합니다.
receptive field는 출력값이 전체 network에서 볼 수 있는 원래의 input 영역을 결정합니다.
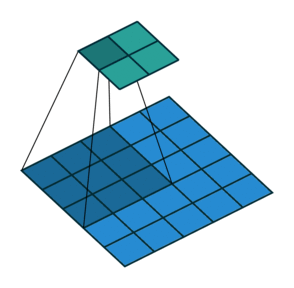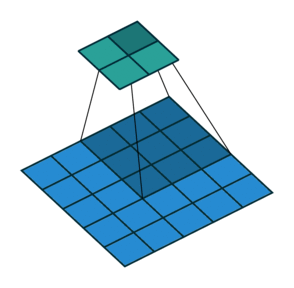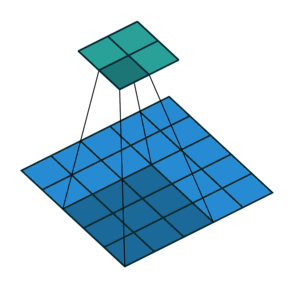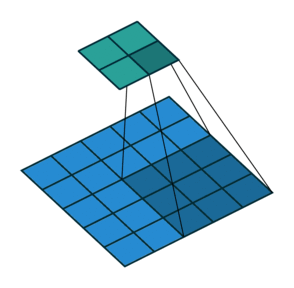
*stride 2인 Pooling layer에서의 convolution입니다.
Pooling은 서브 샘플링(subsampling)이라고도 합니다.
말그대로 출력 값에서 일부분만을 취합니다.
Conv layer에서는 pooling이란 용어를 더 즐겨 사용하므로 서브 샘플링은 알아만 두면 될 듯 합니다.
Pooling은 activation function을 거쳐 나온 출력 맵을 압축하는 역할입니다.
Convolution처럼 가로, 세로 일정 간격으로 feature map을 스캔하고, filter를 곱하는 것이 아닌 feature map을 평균(average)내거나 최댓값(max)을 뽑아내서 사용합니다.
만약 224x224 feature map을 2x2 pooling을 적옹하면 112x112로 줄어들게 됩니다.
풀링은 콘볼루션 처럼 가로, 세로 일정 간격으로 특성 맵을 스캔합니다. 하지만 콘볼루션처럼 필터를 곱하는 것이 아니고 특성 맵의 값을 평균 낸다거나 가장 큰 값을 뽑아서 사용합니다. 만약에 224 x 224 인 특성 맵에 2 x 2 풀링을 적용한다면 아래 그림처럼 결과가 112 x 112 로 줄어들게 됩니다.
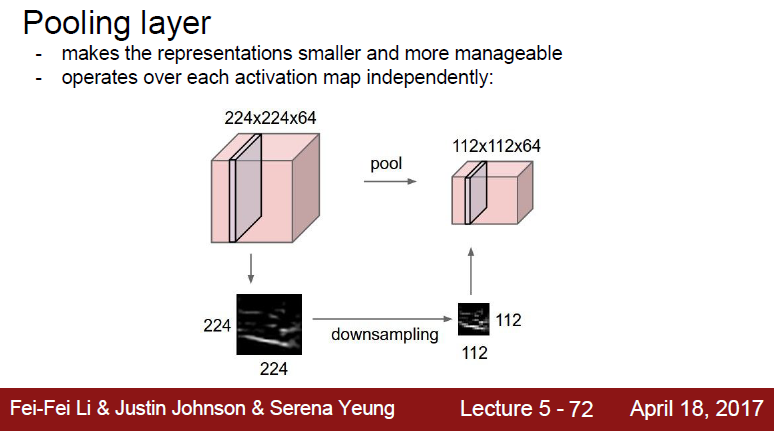
Pooling이 Convolution과 다른 점은, 일반적으로 겹치는 부분 없이 sliding 한다는 점입니다.
기본적으로 Pooling Layer에서는 DownSample을 하는 것이 목적입니다. 따라서 한 지역을 선택하고 값을 하나로 뽑고, 또 다른 지역 선택하고 값을 하나 뽑는 형식으로 진행합니다.
따라서 stride와 동일하게 size를 지정해야 합니다.
아까 output size 공식처럼 Pooling의 입력, 출력 관계를 나타내면 아래와 같습니다.
depth는 동일합니다.
- Average pooling: 평균 값을 계산
- Max Pooing: 최대 값을 선택
Summary
CNN의 기본적인 구조입니다.
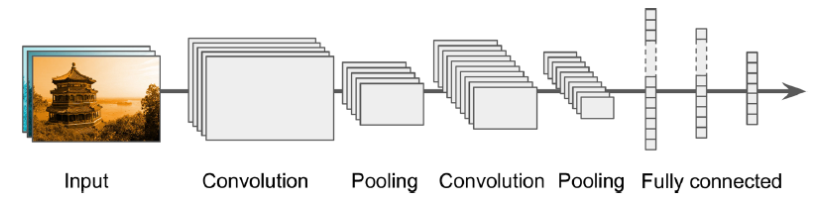
*이미지 출처: 핸즈온 머신러닝
Conv layer와 Pooling Layer가 번갈아가며 있고 마지막 FC-layer를 통해 예측 값을 출력합니다.
Conv layer에는 ReLU와 같은 activation function이 있습니다. activation function이 계산한 출력값으로 Pooling 연산이 진행됩니다.
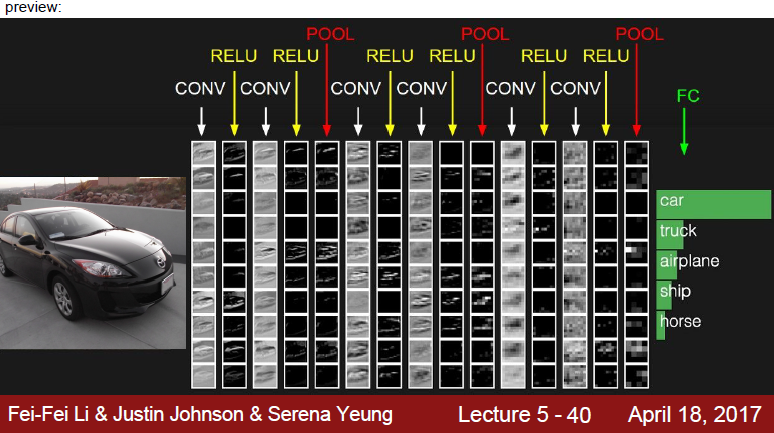
*강의 슬라이드 참고
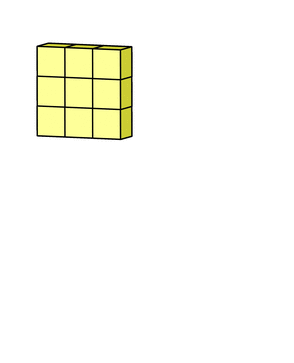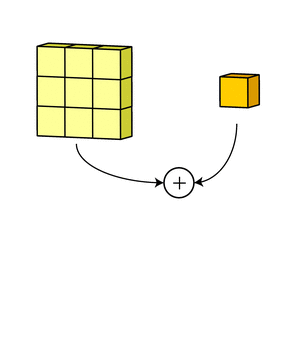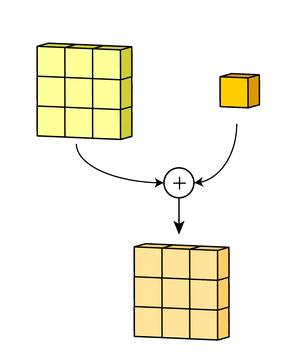
- 3x3 kernel을 가진 filter가 sliding하며 Convolve하는 과정
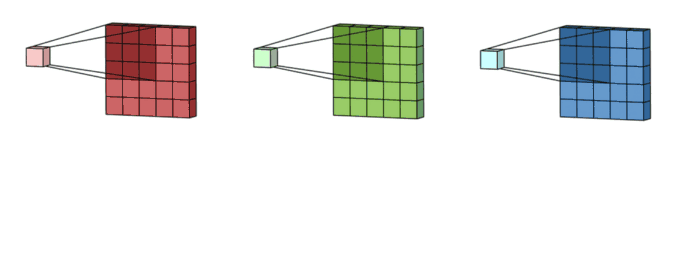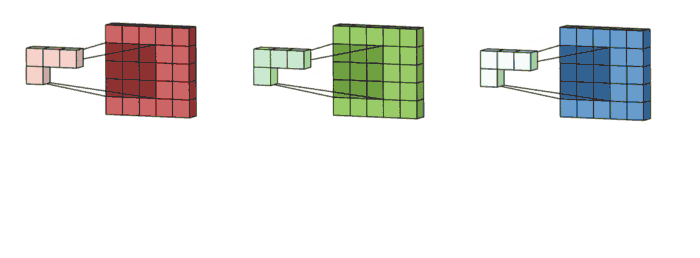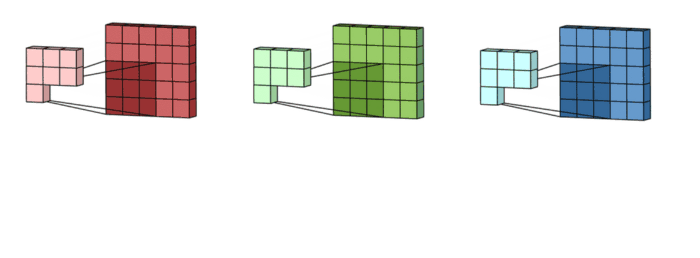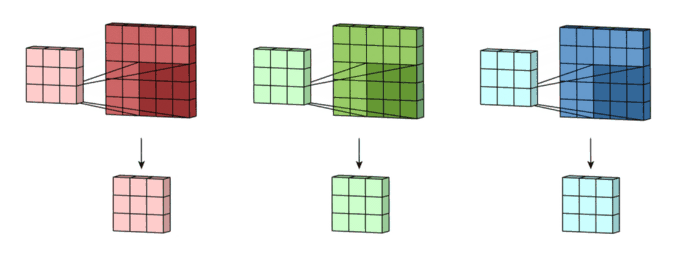
- 각 channel 별로 처리되어 하나의 channel을 만듭니다. filter 전체는 하나의 출력 channel을 만듭니다.
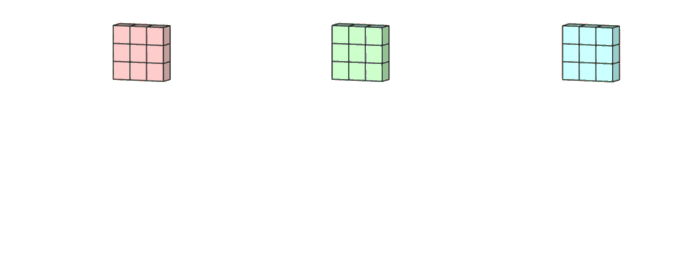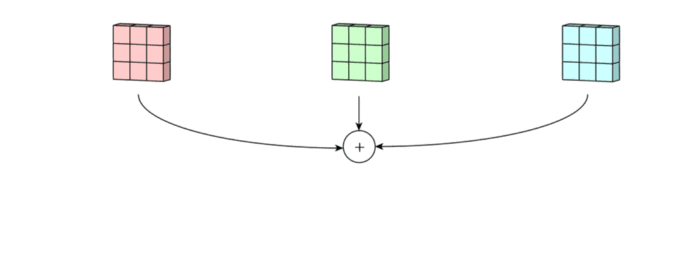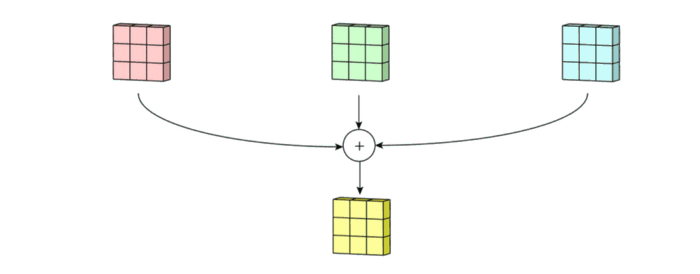
- 마지막에 더해지는 것은 bias입니다. 각 filter의 출력마다 bias가 하나씩 더해져서 최종 출력을 만듭니다.
후기
개인적으로 cs231 강의는 딥러닝을 공부하기에 매우 좋지만, 이번 강의의 슬라이드는 유독 정신 없는 느낌이 많이 들었습니다.
그래서 슬라이드에 따라서 정리하기 보다는 CNN의 개요부터 흐름에 따라 정리해보았습니다.
맨 앞에 적어둔 Reference가 정말 좋은 자료이니, 제 블로그 설명이 부족하면 참고하셨으면 좋겠습니다.
감사합니다.
