cs231n 7강 정리 - Training Neural Networks II

미남로그·2022년 2월 17일

CS231n

목록 보기

6/8

이번 포스팅은 standford university의 cs231 lecture 7을 공부하고, 강의와 슬라이드를 바탕으로 정리한 글임을 밝힙니다.

Reference

💻 유튜브 강의: Lecture 7 | Training Neural Networks Ⅱ
💻 한글 강의: cs231n 6강 Training NN part 2
📑 slide: PDF
📄 Various Optimization Algorithms For Training Neural Network
📄 Ensemble Models
📄 Transfer Learning
📄 A Gentle Introduction to Transfer Learning for Deep Learning

1. Optimization

Optimizer는 loss를 줄이기 위해 weight와 learning rate와 같은 neural network 속성을 변경하는데 사용하는 Algorithm입니다.

Optimization algorithms의 전략은 loss를 줄이고 정확한 결과를 제공하는 역할을 합니다.

같이 살펴보게 될 Algorithms은

Gradient Descent
Stochastic Gradient Descent
Mini-Batch Gradient Descent
Momentum
Nesterov Accelerated Gradient
Adagrad
AdaDelta
Adam

입니다.

1) Gradient Descent

Gradient Descent은 가장 기본적이지만 가장 많이 사용되는 최적화 알고리즘입니다.

linear regression 및 classification algorithms에서 많이 사용됩니다. neural network의 backpropagation은 gradient descent를 사용합니다.

gradient descent는 loss function의 1차 도함수에 의존하는 알고리즘입니다.

함수가 최솟값에 도달할 수 있도록 backpropagation을 통해 weight를 변경하는 방법을 사용합니다.

loss가 한 layer에서 다른 layer로 전달되고 parameter(weight)가 loss에 따라 수정되어 loss를 최소화 할 수 있습니다.

\theta = \theta - \alpha * \nabla J(\theta)

장점

Easy computation.

Easy to implement.

Easy to understand.

단점

local minima에 빠질 수 있다.

전체 데이터셋에 대한 gradient가 계산되면서 Weights가 바뀝니다. 그래서 데이터셋이 엄청 큰 경우 minima의 convergence가 오래 걸립니다.

전체 데이터셋에서 gradient를 계산하기 위해 큰 memory가 필요합니다.

2) Stochastic Gradient Descent

Gradient Descent의 변형입니다. model의 parameter를 더 자주 update하려고 합니다.

여기서는 parameter가 각 training example마다 한 번씩 계산되어 바뀝니다.

그래서 데이터셋이 1,000개의 rows를 갖고 있다면 SGD는 데이터세트의 한 cycle에서 parameter를 1,000번 업데이트합니다.

θ=θ−α⋅∇J(θ;x(i);y(i))

* where ${x(i) ,y(i)}$ are the training examples

모델의 parameter가 자주 업데이트 되어서 손실 함수의 변동이 큽니다.

장점

model parameter를 자주 업데이트하면 더 짧은 시간에 수렴됩니다.

loss function을 저장할 필요가 없으므로 memory가 덜 필요합니다.

새로은 최솟값을 얻을 수 있습니다.

단점

model parameter의 높은 variance

global minima를 달성한 후에도 shooting 할 수 있습니다. (빠져나올 수 있다.)

gradient descent처럼 동일한 convergence를 얻으려면 learning rate를 줄여 천천히 학습해야 합니다.

3) Mini-Batch Gradient Descent

Gradient Descent의 변형 algorithms 중에 가장 좋습니다. SGD와 Gradient Descent을 모두 개선한 방법입니다.

모든 batch 후에 모델 parameter를 업데이트합니다.

따라서 데이터셋은 다양한 배치로 나뉘며 매 배치 후에 parameter가 업데이트 됩니다.

θ=θ−α⋅∇J(θ; B(i))

*where ${B(i)}$ are the batches of training examples.

장점

model parameter를 자주 업데이트하고 variance도 작습니다.

중간 정도의 memory가 필요합니다.

모든 유형의 gradient descent에는 몇 가지 문제가 있는데요.

단점

learning rate의 최적값을 선택합니다. learning rate가 너무 작으면 converge하는데 시간이 걸릴 수 있습니다.

모든 parameter에 대해 일정한 learning rate를 유지합니다. (같은 비율로 변경하고 싶지 않은 일부 parameter가 있어도 )

local minima에 빠질 수 있습니다.

4) Momentum

Momentum은 SGD의 높은 분산을 줄이고 수렴을 더 부드럽게 하기 위해 만들어졌습니다.

최솟값의 방향으로는 수렴을 가속화하고 관련 없는 방향으로는 변동을 줄입니다.

이 방법에서는 $γ$ 가 momentum이라는 hyper parameter가 사용됩니다.

V(t)=γ*V(t−1)+α*∇J(θ)

이제 가중치는 $\theta= \theta-v(t)$ 로 업데이트됩니다.

운동량 $γ$ 은 일반적으로 0.9 또는 유사한 값으로 설정됩니다.

장점

parameter가 진동하는 것을 줄입니다. (*변동을 줄임)

Gradient Descent보다 빠르게 수렴합니다.

단점

수동으로 정확히 선택해야 하는 hyper parameter가 하나 더 늘었습니다.

5) Nesterov Accelerated Gradient

momentum이 좋은 방법일 수 있지만 너무 높으면 알고리즘이 local minima를 놓치고 계속 상승합니다.

이 문제를 해결하기 위해 NAG가 만들어졌습니다!

가중치를 수정하기 위해 $γV(t−1)$ 을 사용하고, $θ−γV(t−1)$ 는 대략적으로 위치를 알려줍니다.

이제 parameter가 아닌

V(t)=γV(t−1)+α * ∇J(θ−γV(t−1))

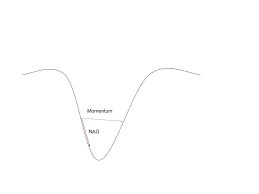
NAG vs momentum at local minima

$θ=θ−V(t)$ 을 통해 parameter를 업데이트합니다.

장점

global minima를 놓치지 않습니다.

local minima를 만나면 느려집니다.

단점

hyper parameter의 수동 선택

6) Adagrad

현재까지 설명된 모든 opimizer의 단점 중 하나는 learning rate가 모든 parameter와 각 주기에 대해 일정하다는 것인데요.

Adagrad는 learning rate를 변경합니다.

각 parameter와 모든 시간 단계 $t$ 에 대해 학습률 $η$ 를 변경합니다.

g_{t,i} = \nabla_\theta J(\theta_{t,i})

주어진 시간 t에서 주어진 매개변수에 대한 손실 함수의 도함수

\theta_{t+1, i} = \theta_{t,i} - \frac{η}{\sqrt{G_{t,ii}+ \epsilon}}*g_{t,i}

주어진 입력 i 및 시간/반복 t에 대한 매개변수 업데이트

$η$ 은 주어진 매개변수 $θ(i)$ 에 대해 계산된 이전 기울기를 기반으로 주어진 시간에 주어진 매개변수 $θ(i)$ 에 대해 수정된 학습률입니다.

기울기 제곱합 $θ(i)$ 을 시간 단계 $t$ 까지 저장하는 반면 $ϵ$ 는 0으로 나누기를 피합니다. 보통 1e−8 정도로 설정합니다.

제곱근 연산이 없으면 알고리즘의 성능이 훨씬 나빠집니다.

덜 빈번한 매개변수에 대해서는 크게 업데이트하고 빈번한 매개변수에 대해서는 작은 단계를 수행합니다.

장점

각 훈련 매개변수에 대한 learning rate 변경

learning rate를 수동 조절할 필요가 없음

Sparce data에 대해 학습할 수 있음

단점

2차 도함수를 계산해야 해서 계산 비용이 많이 듦

learning rate는 항상 느린 training의 결과를 감소시킵니다.

7) RMSProp

RMSProp은 AdaGrad에서 학습이 안 되는 문제를 해결하기 위해 hyper parameter인 $\beta$ 가 추가되었습니다.

변화량이 더 클수록 학습률이 작아져서 조기 종료되는 문제를 해결하기 위해 학습률 크기를 비율로 조정할 수 있도록 제안된 방법입니다.

RMSProp은 최근 경로의 곡면 변화량을 측정하기 위해 지수가중이동평균을 사용합니다.

장점

미분값이 큰 곳에서는 업데이트 할 때 큰 값으로 나눠주기 때문에 기존 학습률 보다 작은 값으로 업데이트 된다. -> 진동을 줄이는데 도움

단점

미분값이 작은 곳에서 업데이트시 작은 값으로 나눠주기 때문에 기존 학습률보다 큰 값으로 업데이트 된다.

이는 조기 종료를 막으면서도 더 빠르게 수렴하는 효과를 불러옵니다.

따라서 최근 경로의 gradient는 많이 반영되고 오래된 경로의 gradient는 작게 반영됩니다.

gradient 제곱에 곱해지는 가중치가 지수승으로 변화하기 때문에 지수가중평균이라 부릅니다.

매번 새로운 gradient 제곱의 비율을 반영하여 평균을 업데이트 하는 방식입니다.

8) Adam

Adam은 1차, 2차 모멘텀으로 작동합니다. global minima를 찾다가 최솟값을 뛰어넘을 수 있기 때문에 너무 빨리 굴러가는 것을 원하지 않습니다.

신중하게 속도를 약간 낮추기를 원하고, Adam은 gradient $M(t)$ 가 기하급수적으로 감소하는 평균을 유지합니다.

$M(t)$ 및 $V(t)$ 는 각각 Mean인 첫 번째 모멘트와 기울기의 uncentered variance인 두 번째 모멘트의 값입니다.

\hat m_t = \frac{m_t}{1-\beta^t_1}

\hat v_t = \frac{v_t}{1-\beta^t_2}

여기서 E[m(t)]가 E[g(t)]와 같을 수 있도록 $M(t)$ 및 $V(t)$ 의 평균을 취합니다.

매개변수를 업데이트합니다.

\theta_{t+1} = \theta_{t} - \frac{η}{\sqrt{\hat v_t+ \epsilon}}*\hat m_{t}

$\beta_1$ 의 값은 0.9, $\beta_2$ 의 경우 0.999, $ϵ$ 의 경우 (10 x exp(-8)) 값을 기본적으로 씁니다 .

장점

너무 빠르고 빠르게 수렴됩니다.

vanishing learning rate와 high variance를 수정됩니다.

단점

계산 비용이 많이 듭니다.

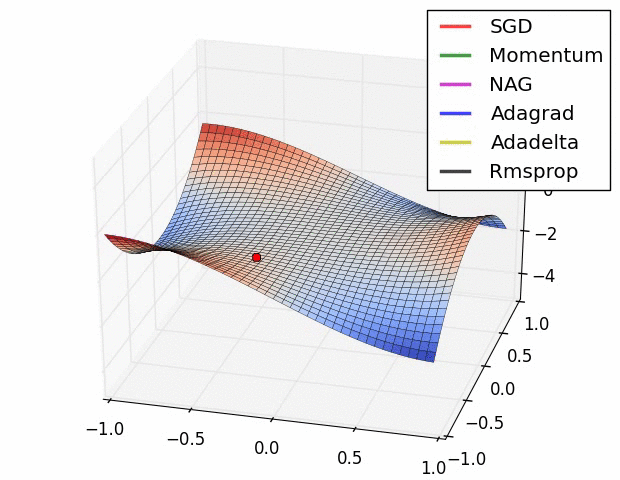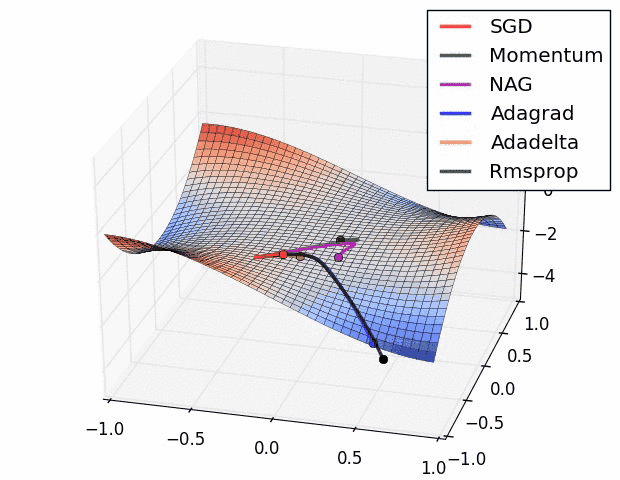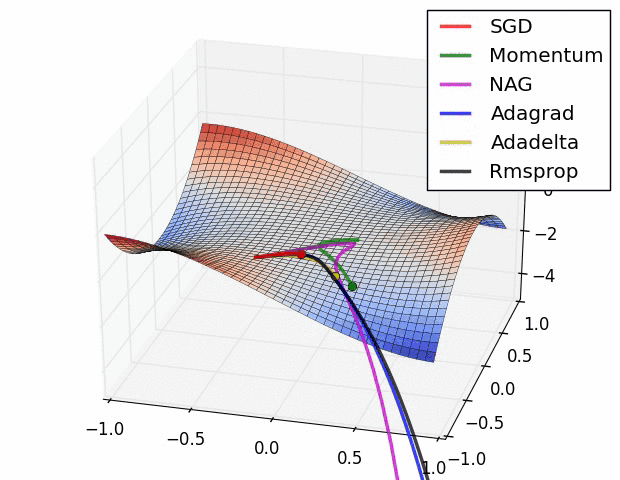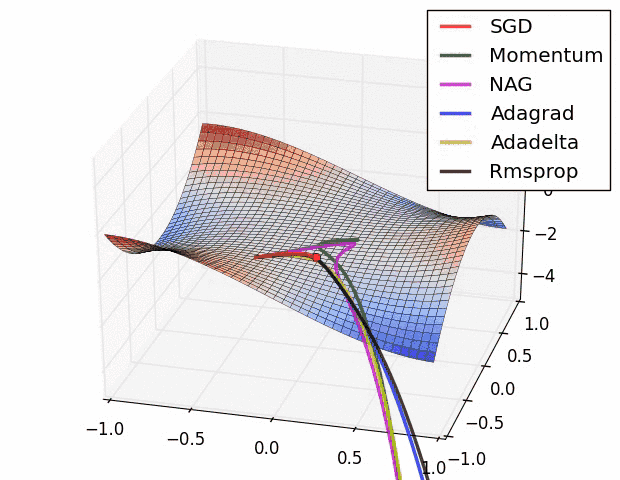
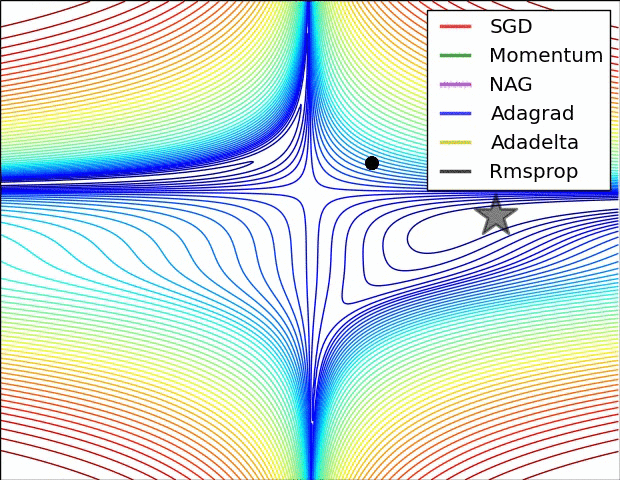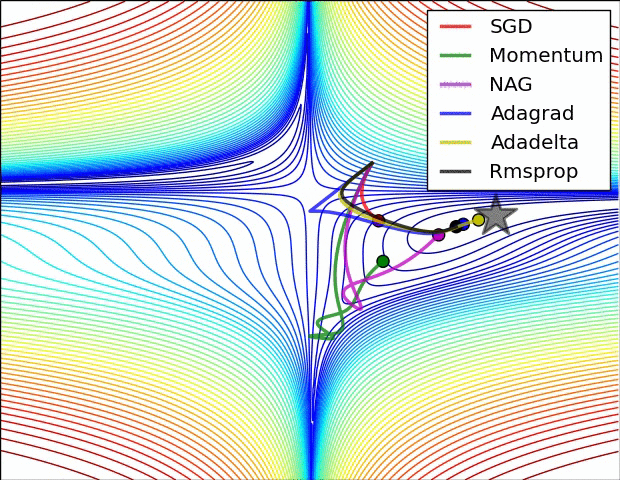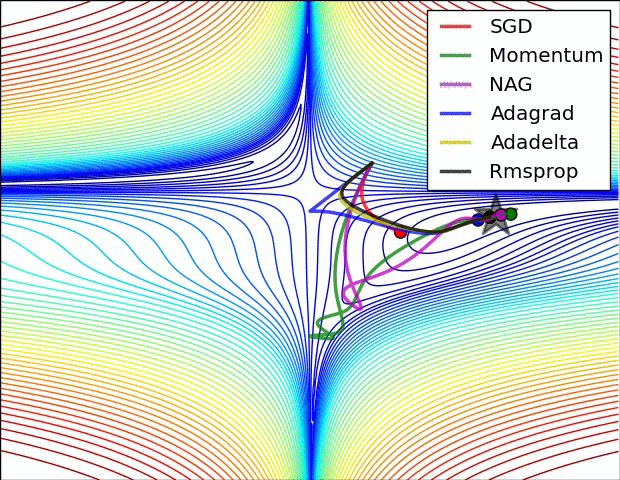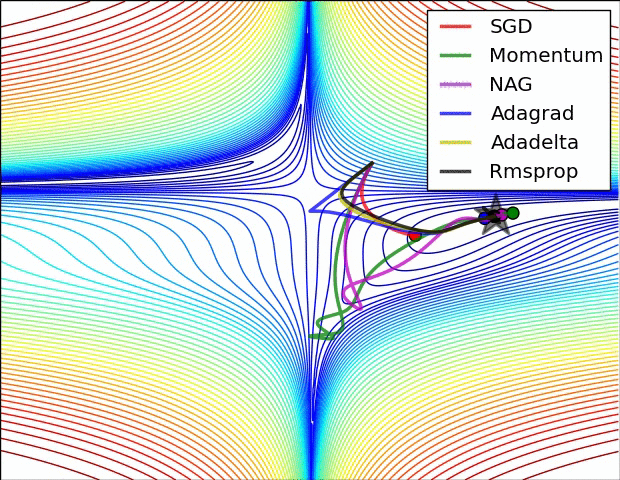
강의에서는 코드와 같이 설명하고 있고요.

마지막에 질문을 던집니다.

Q: Which one of these learning rates is best to use?

이중에 어떤 것도 최선이 아니다.
learning rate를 점점 decay 시키는 것이 가장 좋다.

요약하자면,

Adam은 많은 것들 중 가장 좋은 기본 선택지이며, 전체적으로 업데이트 해볼 수 있다면 시도해보는 것이 좋다고 합니다.

2. Ensemble Models

Ensemble models은 prediction process에서 여러 다른 모델을 결합하는 machine learning 접근 방식입니다.

이러한 모델을 기본 추정량이라고 합니다. 단일 추정기를 구축하는 다음과 같은 기술적 과제를 극복하기 위한 솔루션입니다.

High variance: 모델은 학습된 feature에 제공된 inputs에 매우 민감합니다.
Low accuracy: 전체 훈련 데이터에 맞는 하나의 모델 또는 하나의 알고리즘이 기대치를 충족하기에 충분하지 않을 수 있습니다.
Features noise and bias: 이 모델은 예측을 하는 동안 하나 또는 몇 가지 feature에 크게 의존합니다.

single algorithm은 주어진 dataset에 대해 완벽한 예측을 못할 수 있습니다.

machine learning에는 한계가 있으며 높은 정확도로 모델을 생성하는 것은 어렵습니다.

여러 모델을 만들고 결합하면 전체 정확도가 향상될 수 있습니다.

이는 모델 error를 줄이고 일반화를 유지하는 두 가지 목표로 모델의 출력을 구현할 수 있고, 몇 가지 기술을 사용하여 달성할 수 있습니다.

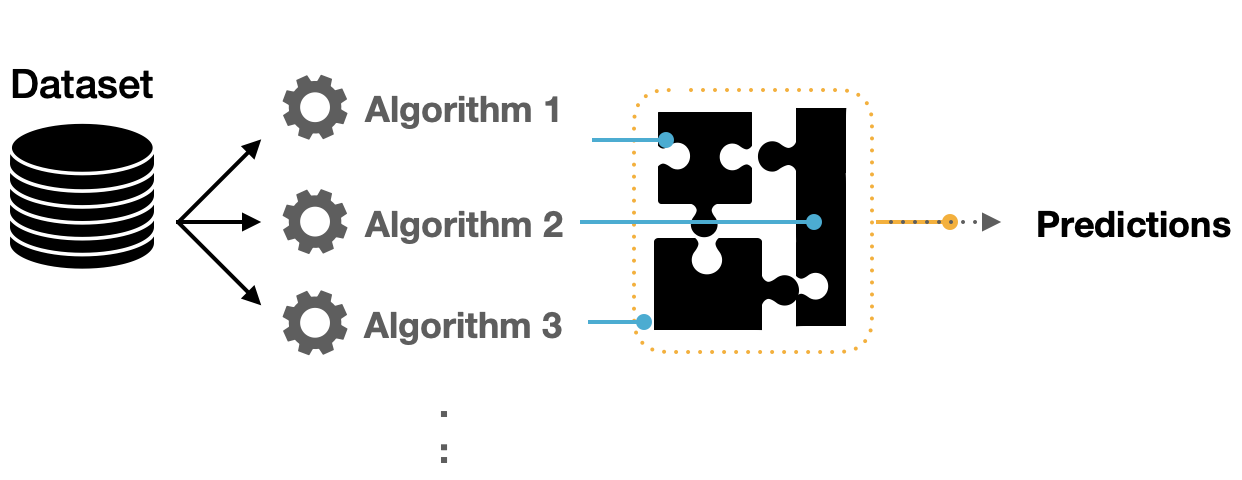
여러 independent model을 학습합니다.
test time에 결과를 평균냅니다.

1) Same model, different initializations

cross-validation을 사용해서 가장 좋은 hyper parameter를 결정한 다음,

random initialization가 다른 여러 모델을 훈련합니다.

이 방식이 위험한 이유는 다양성이 initialization로 인한 것 뿐이라는 것입니다.

2) Top models discovered during cross-validation

cross-validation을 사용해서 최적의 hyper parameter를 결정한 다음 상위 몇 개 모델(예를 들어, 10개)을 선택하여 ensemble을 구성합니다.

이는 ensemble의 다양성을 향상 시키지만 차선의 모델을 포함할 위험이 있습니다.

실제로 cross-validation 후에 모델을 추가로 retraining 할 필요가 없으므로 이 작업을 수행하는 것이 더 쉬울 수 있습니다.

3) Different checkpoints of a single model

training이 매우 비용이 많이 드는 경우에, 일부 사람들은 시간이 지남에 따라 single network의 다른 checkpoints를 취해 (예를 들어, 매 epoch마다) ensemble을 형성하는데 제한적으로 성공했습니다.

이건 다양성이 부족하긴 하지만 여전히 training에서는 잘 작동합니다.

이 접근 방법의 장점은 비용이 적게 든다는 것입니다.

4) Running average of parameters during training

마지막 point와 관련하여 거의 항상 2%의 성능을 얻는 방법은 training 중에 이전 가중치의 기하급수적으로 감소되는 합계를 유지하는 네트워크 가중치를 메모리에 유지하는 방법입니다.

이렇게 하면 지난 몇 번의 반복에 대한 네트워크 상태를 평균화 할 수 있습니다.

지난 몇 단계에 거쳐 부드러워진 가중치는 거의 항상 더 나은 validation error를 달성합니다.

3. Data Augmentation

Data Augmentation의 두 가지 접근 방법이 있습니다.

1) Why is data augmentation necessary?
2) How is data augmentation done?

이 두 가지이고, 아래의 분야에서 활용됩니다.

in computer vision
in natural language processing

Data Augmentation은 Overfitting의 문제를 해결하는 방법입니다.

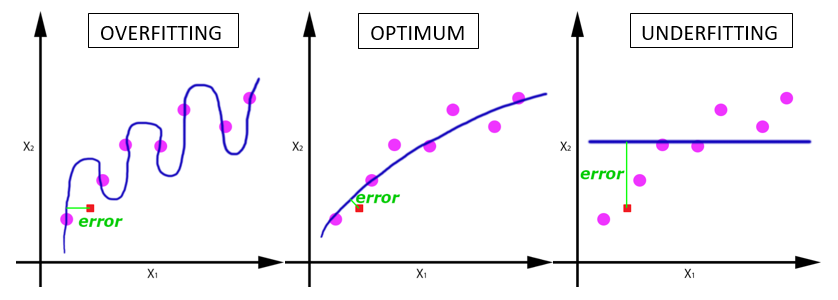
Overfitting은 위 그림으로 보았을 때

모델이 training data (O)에만 너무 잘 맞고, unseen data ( (□))에는 잘 맞지 않는 경우를 말합니다.
이상적으로 항상 잘 맞는 spot을 찾고 싶습니다.

다른 해결 책으로는 정규화 기법이 있습니다. 이는 모델 복잡성을 줄일 수 있습니다.

L2 normalization, dropout, ensembles, label smoothing, etc

이의 가장 근본적인 해결 방법은 training data를 늘리는 것이 있고, 또 다른 방법으론 아래 세 가지가 있습니다.

Collect more
- Expensive
- EXPENSIVE
- E.X.P.E.N.S.I.V.E
Synthesize
- Complicated
- Little variation
- Mode collapse
Augment
- Simple
- Well-studied
- Which is optimal?

여기서 3번이 소개할 Data Augmentation입니다.

강의에서 Data Augmentation으로 소개된 항목들은

Horizontal Flips

Random crops and scales

Color Jitter

등 이외에

이러한 것들이 있습니다.

Regularization의 다른 방법으로 Dropout, Batch Normalization, Data Augmentation 등이 소개되고 있습니다.

다음에 나오는 내용은 Dropout에 해당됩니다.

Conclusions

Data augmentation reduces overfitting on the training data.
Various techniques have been developed for CV & NLP.
Subfields of machine learning that leverage data augmentation
- Semi-supervised learning w/ consistency regularization
- Self-supervised contrastive learning
Data augmentation for other data domains
- Audio
- Graphs
- Structured tabular data

4. Regularization: Dropout

Dropout에 대해 이전에 정리한 포스팅이 있습니다. 기본적인 내용은 같기 때문에 해당 포스팅을 첨부합니다.

📄 Dropout (드롭아웃) regularization
📄 드롭아웃(Dropout)

해당 내용을 📗[핸즈온 머신러닝 2판] 교재를 바탕으로 정리했습니다.

드롭아웃은 심층 신경망에서 가장 인기 있는 규제 방법 중 하나입니다.

매 training step에서 각 뉴런은 임시적으로 드롭아웃 될 확률 $p$ 를 가집니다.

즉, 이번 training에서는 완전히 무시되어도 다음 스텝에서는 활성화 될 수 있습니다.

이 $p$ 가 dropout rate라 부르며, 하이퍼 파라미터에 속합니다.

테스트 할 때는 드롭아웃을 사용하지 않는데요. 그렇다보니 만약 $p=0.5$ 로 했다면 테스트 하는 동안에는 하나의 뉴런이 훈련 때보다 2배 더 많은 input neuron과 연결됩니다.

이런 점을 보상하기 위해 훈련하고 나서 각 뉴런의 연결 가중치에 0.5를 곱할 필요가 있습니다.

그렇지 않으면, 각 뉴런이 훈련한 것보다 거의 두 배 많은 입력 신호를 받기 때문에 잘 동작하지 않습니다.

훈련이 끝난 뒤 각 입력의 연결 가중치에 보존 확률(keep probability, $1-p$ )를 곱해야 한다.

또는 훈련하는 동안 각 뉴런의 출력을 보존 확률로 나눌 수도 있습니다.

만약 드롭아웃을 사용했을 때, 모델이 과적합되었다면?

드롭아웃 비율을 늘려줍니다.

반대로 모델이 훈련 세트에 과소적합되면 드롭아웃 비율을 낮춰야 합니다.

layer가 클 때는 드롭아웃 비율을 늘리고, 작은 층에는 비율을 낮추는 것도 도움이 됩니다.

최신의 neural network 구조는 마지막 layer에만 드롭아웃을 사용하기도 합니다.

+ 추가 내용: Ensemble은 Dropout과 밀접합니다. 드롭아웃이 학습 떄 뉴런을 무작위로 삭제하는 행위를 매번 다른 모델을 학습시키는 것으로 해석할 수 있습니다. 그리고 추론 때는 뉴런의 출력에 삭제한 비율 등을 곱함으로써 앙상블 학습에서 여러 모델의 평균을 내는 것과 같은 효과를 얻습니다.

즉, 드롭아웃은 앙상블과 같은 효과를 하나의 network로 구현했다고 생각할 수 있습니다.

5. Transfer learning

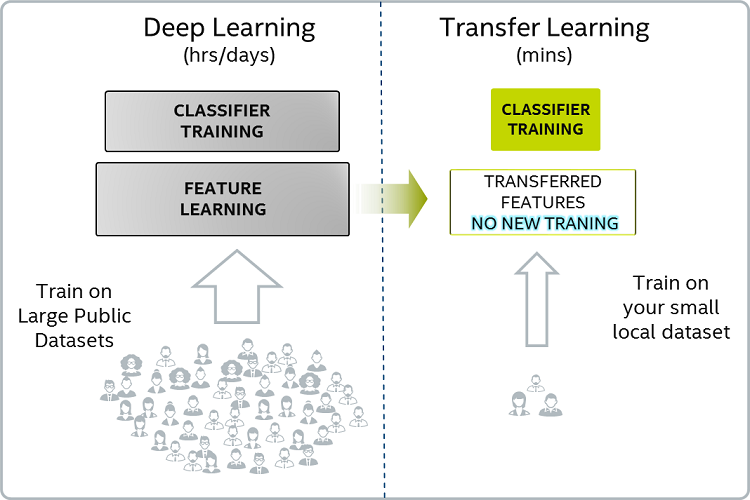
Transfer Learning이란 무엇일까요?

Transfer Learning은 전이학습이라고도 합니다.

Transfer Learning의 일반적인 아이디어는 label이 있는 data가 거의 없는 경우에 label이 있는 data가 많은 작업에서 학습한 지식을 사용하는 것입니다.

label을 지정하는 것은 비용이 많이 들기 때문에 기존 데이터 세트를 최적으로 활용하는 것이 중요합니다.

전통적인 machine learning model에서 주요 목표는 training data에서 학습한 패턴을 기반으로 unseen data를 일반화하는 것입니다.

Transfer Learning을 사용하면 다른 작업에 대해 학습된 패턴에서 시작하여 일반화 과정을 시작합니다. 기본적으로 (종종 무작위로 초기화되는) 빈 시트에서 학습 프로세스를 시작하는 대신 다른 작업을 해결하기 위해 학습된 패턴에서 시작합니다.

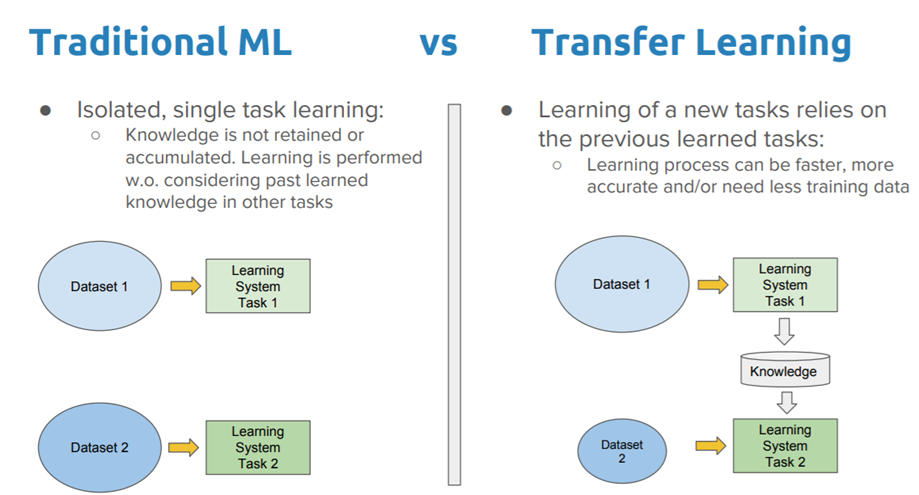
Transfer Learning은 모든 종류의 학습에서 필수적입니다. 비유로 설명하자면 사람은 성공하기 위해 모든 단일 작업과 문제를 학습하지 않습니다.

누구나 한 번도 경험하지 못한 상황에 처하게 되고, 여전히 그때마다 문제를 해결합니다.

수많은 경험에서 배우는 능력과 ‘지식(knowledge)’을 새로운 환경으로 내보내는 것이 전이학습의 전부라고 볼 수 있습니다.

Transfer Learning은 딥러닝 연구의 거의 모든 곳에서 사용되는 핵심 기술이기도 하지만, 실제로는 모델을 훈련하기 위한 수백만 개의 레이블이 지정된 data point가 없습니다.

딥러닝 기술은 신경망에서 수백만 개의 매개변수를 조정하기 위해 엄청난 양의 데이터를 필요로 합니다.

특히 supervised learning의 경우 많은 label이 지정된 data가 필요합니다.

image에 label을 지정하는 것은 사소해 보이지만, 자연어 처리에서 label이 지정된 large dataset을 생성하려면 전문 지식이 필요합니다.

Transfer Learning은 neural network가 실행 가능한 옵션이 되기 위해 필요한 dataset의 크기를 줄이는 한 가지 방법입니다.

다른 방법으로는 일반적으로 제한된 dataset을 다루기 위해 더 적합한 모델을 향해 데 더 적합한 모델로 이동합니다.

Transfer Learning은 장점과 ㄷ나점이 있습니다. 단점을 이해하는 것은 machine learning program에 중요합니다.

Knowledge의 이전은 ‘적절한’ 경우에만 가능합니다. 이 맥락에서 ‘적절한’의 의미를 정의하긴 어려우며, 일반적으로 실험이 필요합니다.

Transfer Learning에도 동일한 원칙이 적용되는데요. 예를 들어, 페라리와 장난감 자동차 같은 차이를 의미합니다.

정량화하긴 어렵지만 Transfer Learning에도 상한선이 있다는 의미입니다. 모든 문제에 맞는 solution이 될 수 없습니다.

Transfer Learning은 한 domain에서 다른 domain으로 knowledge를 transfer 할 수 있는 능력이 필요합니다.

많은 NLP 문제가 본질적으로 sequence 예측 문제로 축소될 수 있기 때문에 NLP model architecture를 sequence 예측 문제에서 재사용할 수 있습니다.

Transfer Learning은 실제로 다른 모델에서 한 모델의 parameter를 reuse하는 낮은 수준에서 해석되기도 합니다.

Transfer Learning이 사용되는 경우?

이는 최적화이기도 하며 시간을 절약하고 더 좋은 성능을 얻을 수도 있습니다.

higher slope

higher start

higher asymptote

이상적으로 전이 학습을 성공적으로 적용하면 위의 이점이 나타납니다. 더 많은 데이터로 관련 작업을 진행할 수 있고, 재사용할 수 있는 resource가 됩니다.

data가 충분하지 않은 문제에서 이를 사용하면 더 나은 모델을 개발할 수 있습니다. (어떤 source data를 선택할 것인지는 domain에 대한 지식 및 직관이 필요합니다.)

이번에도 강의 내용을 바탕으로 Reference를 통해 필요한 내용을 정리하였습니다! 내용에 잘못된 부분이 있으면 지적 부탁드립니다. 감사합니다!

미남로그

미남이 귀엽죠

이전 포스트

cs231n 6강 정리 - Training Neural Networks I

다음 포스트

cs231n 9강 정리 - CNN Architectures

2개의 댓글

Kim

2022년 3월 22일

엄청 정리가 잘 돼있네요 좋은글 감사합니다.

1개의 답글