머신러닝에 필요한 기초 수학 정리

저는 한빛미디어의 '파이썬으로 배우는 머신러닝의 교과서' 책을 바탕으로 내용을 직접 필기하여 정리하였습니다.

내용의 출처는 모두 해당 책임을 밝히며, 책으로 보고 싶으신 분들은 'CHAPTER 4 머신러닝에 필요한 수학의 기본'을 참고하시면 됩니다.

필기 자료를 사용하실 경우, 출처를 밝혀주시거나 댓글로 알려주세요.

감사합니다.🙂

편미분

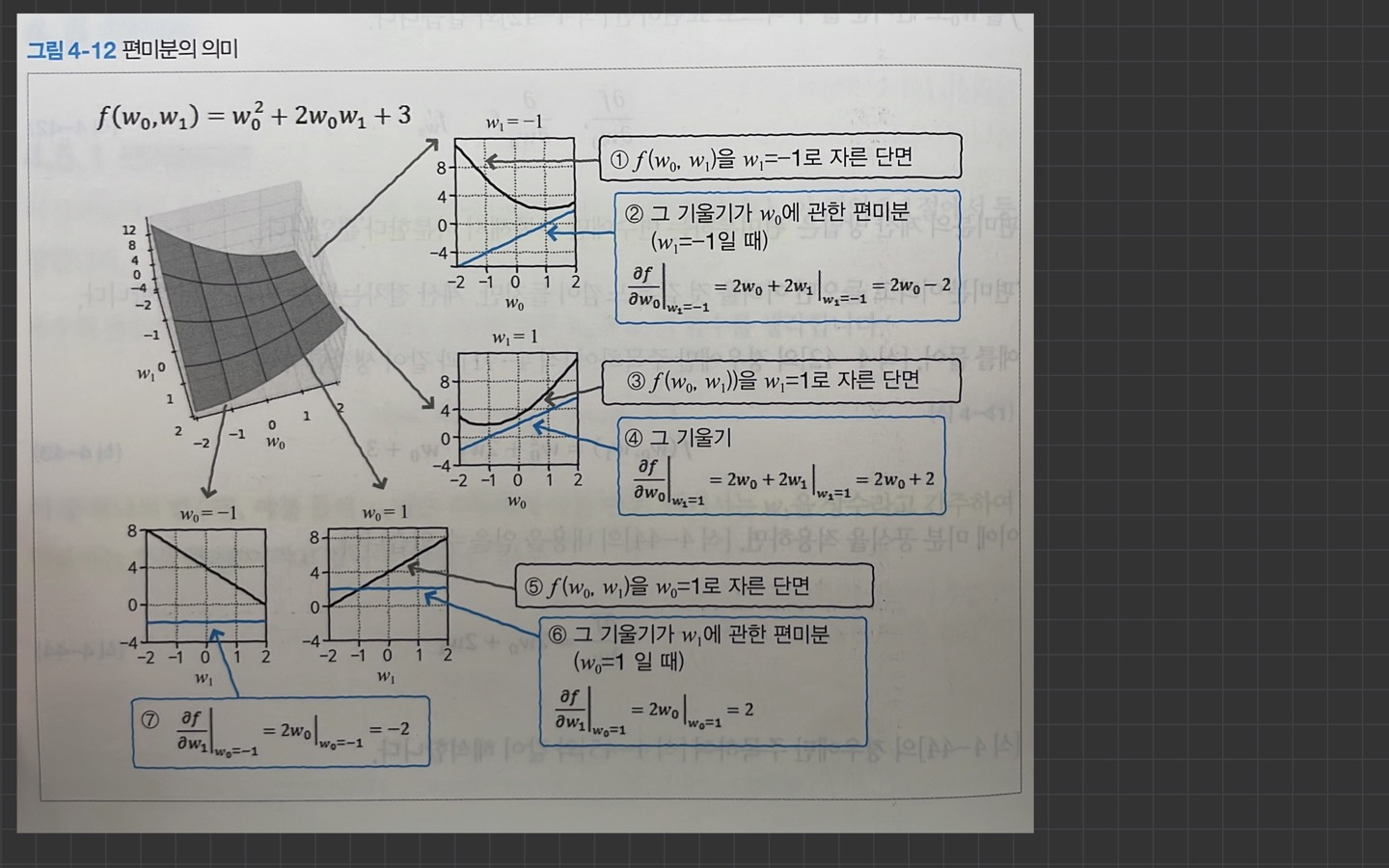
다변수의 중첩 함수의 미분

내부 함수가 3개 이상이라면, 어떻게 편미분을 진행하는지

편미분은 backpropagation에서 gradient를 구할 때 알고 있어야 하는 파트입니다.

행렬과 연립방정식

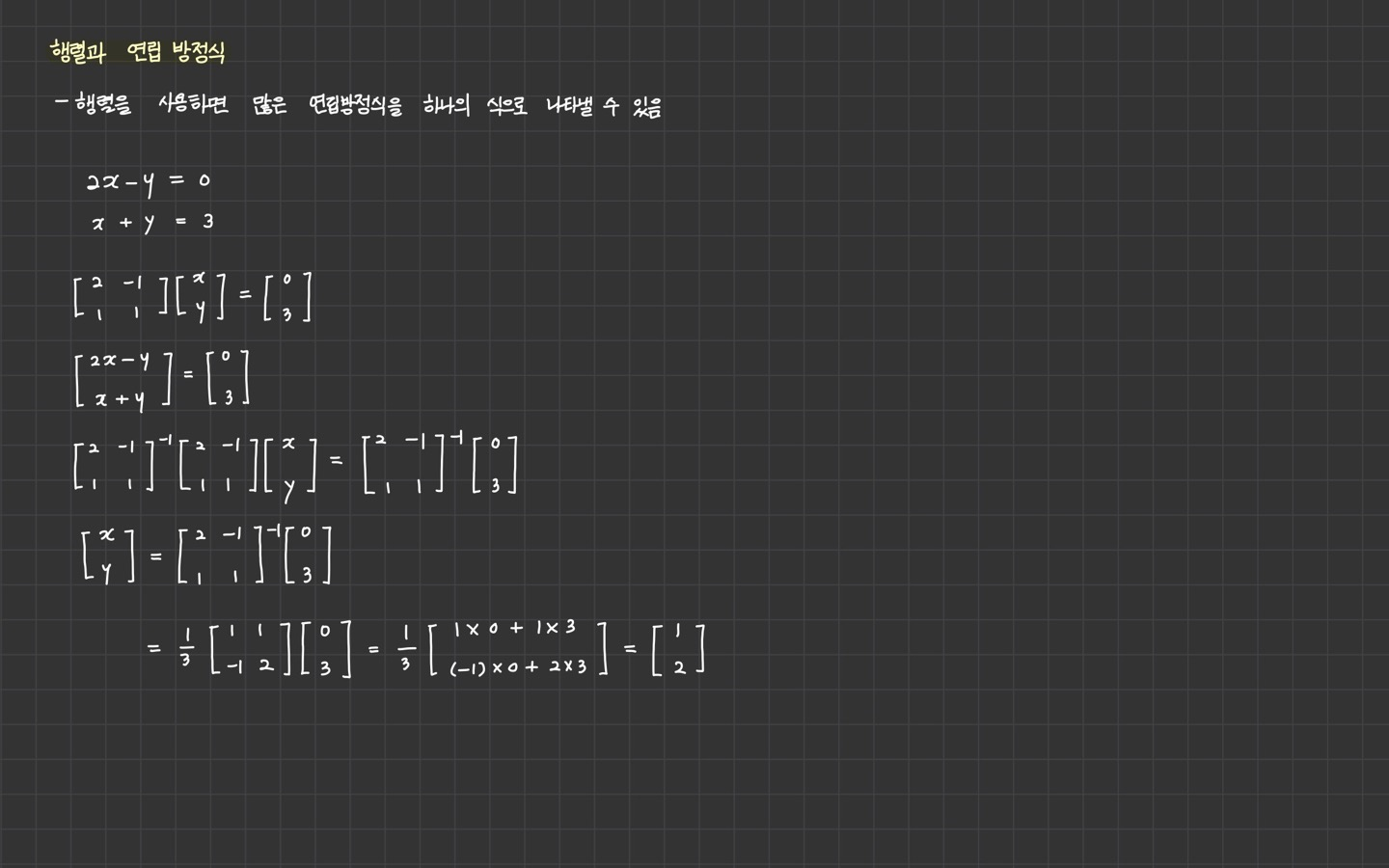
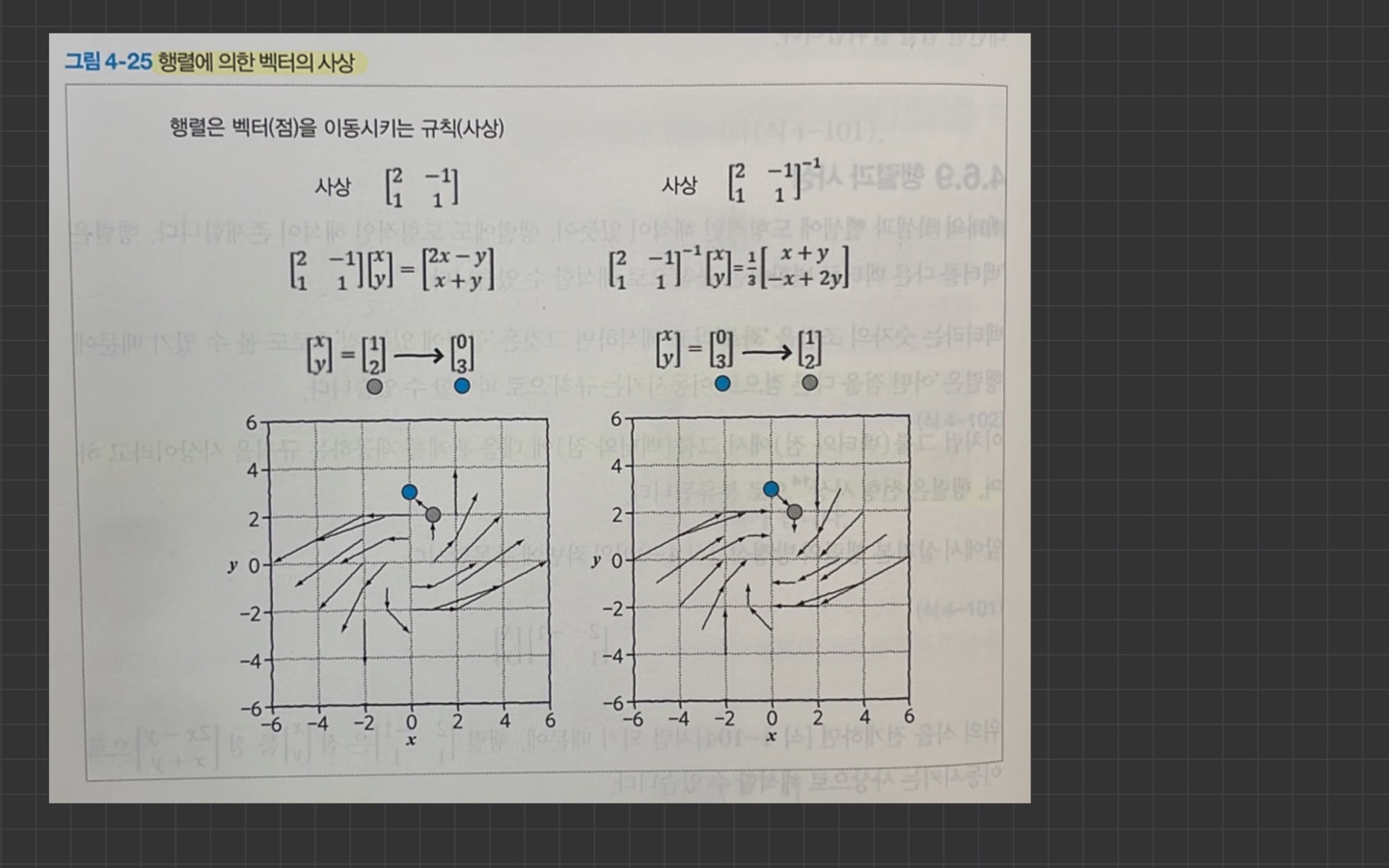
행렬과 사상

저는 linear mapping과 linear transformation, linear operation의 개념이 다 따로 놀았는데,

이번을 기회로 되게 깔끔하고 쉽게 개념을 이해할 수 있었습니다.

선형결합을 보존하는 두 벡터 공간 사이의 함수

지수와 로그

로그의 성질

곱셈은 덧셈으로 변환된다.

로그는 단조증가 함수로서 로그를 취해도 최솟값, 최댓값을 취하는 값은 변하지 않는다.

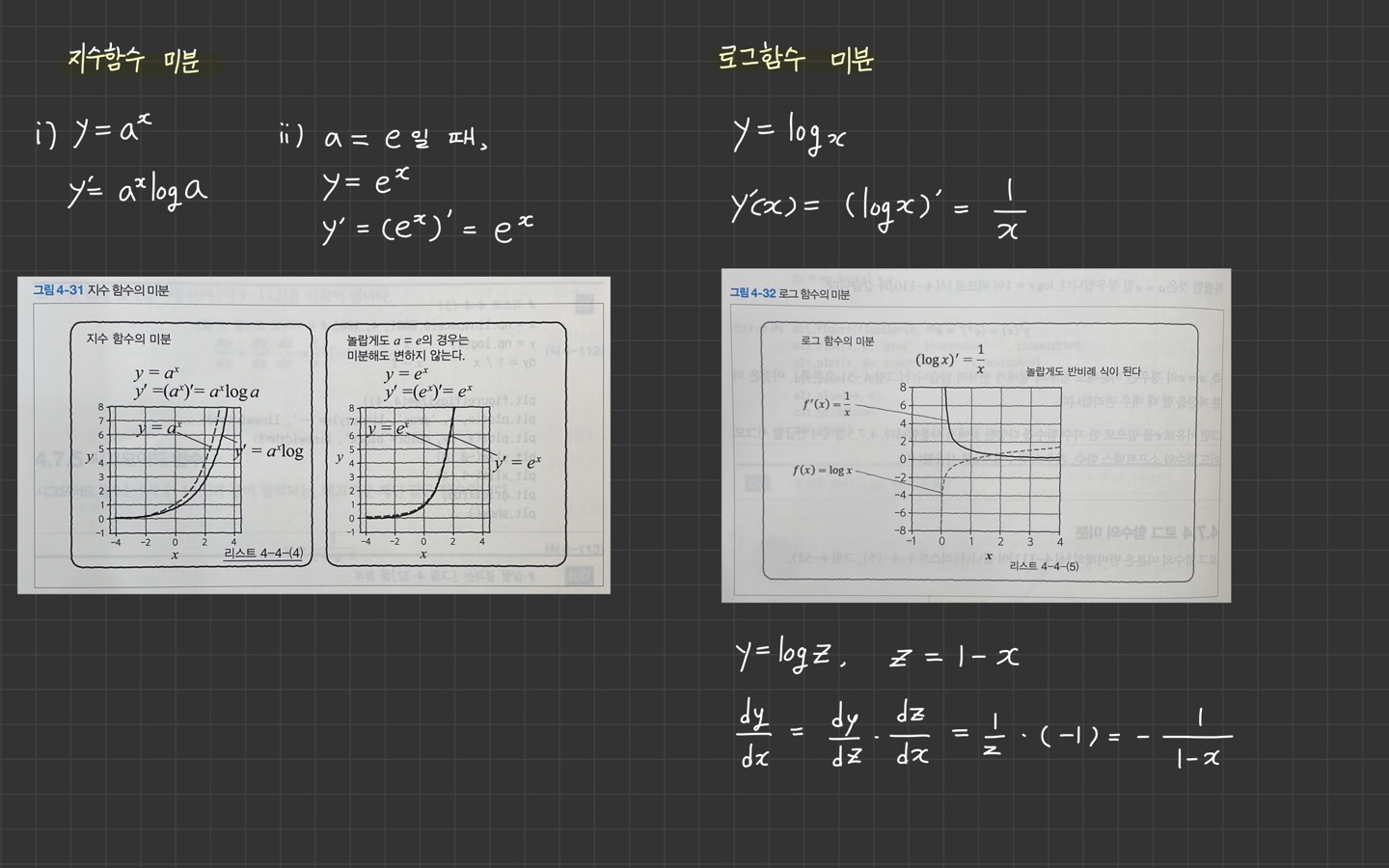
지수함수, 로그함수의 미분

시그모이드 함수

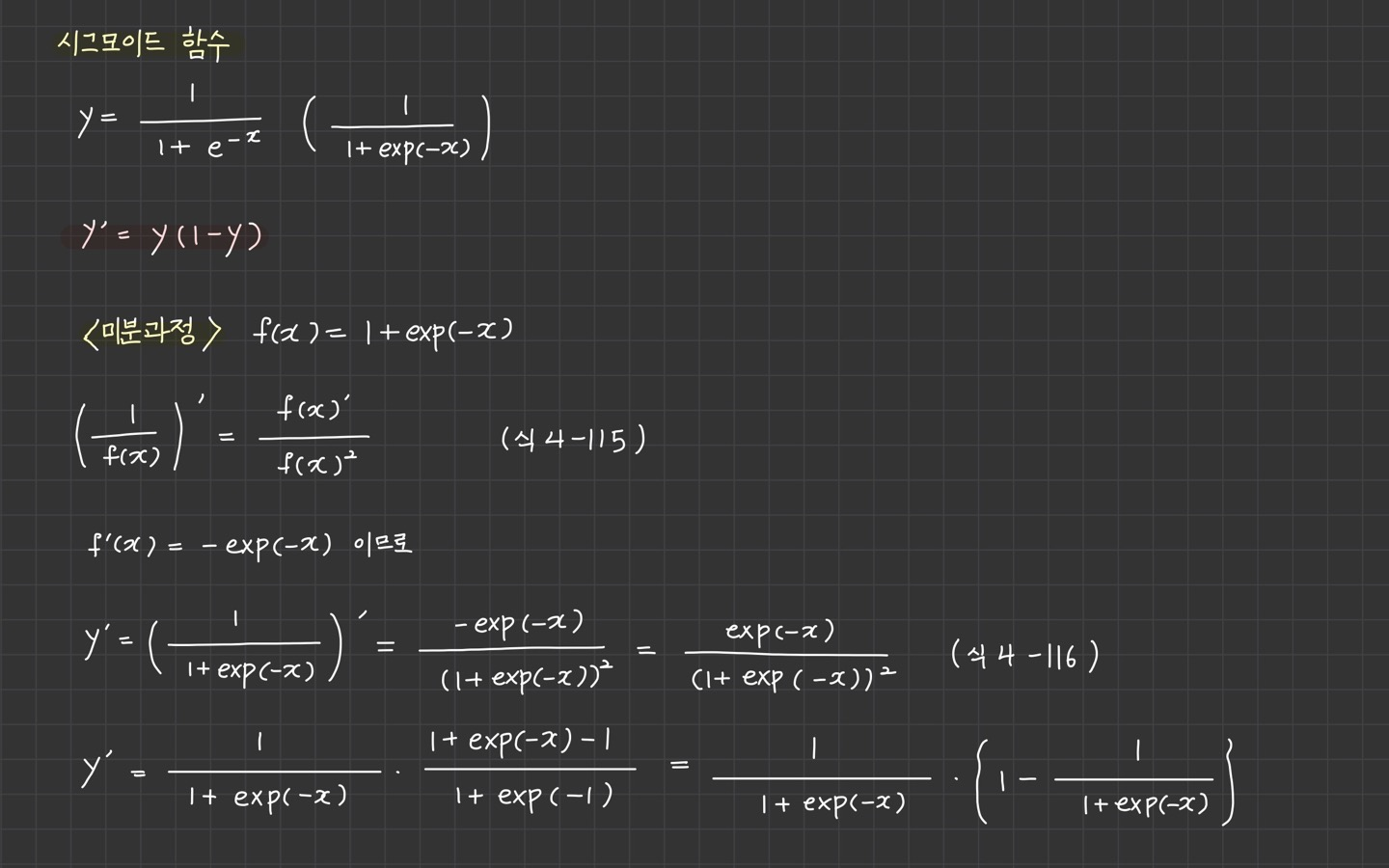
시그모이드 함수의 식과 미분 식에 익숙해지면, 나중에 어떤 개념을 이해하는데 더 빠르게 이해할 수 있는 것 같습니다.

소프트맥스 함수

변수가 k개(2개 이상)일 때의 소프트맥스 함수 식입니다.

소프트맥스와 시그모이드 함수 관계

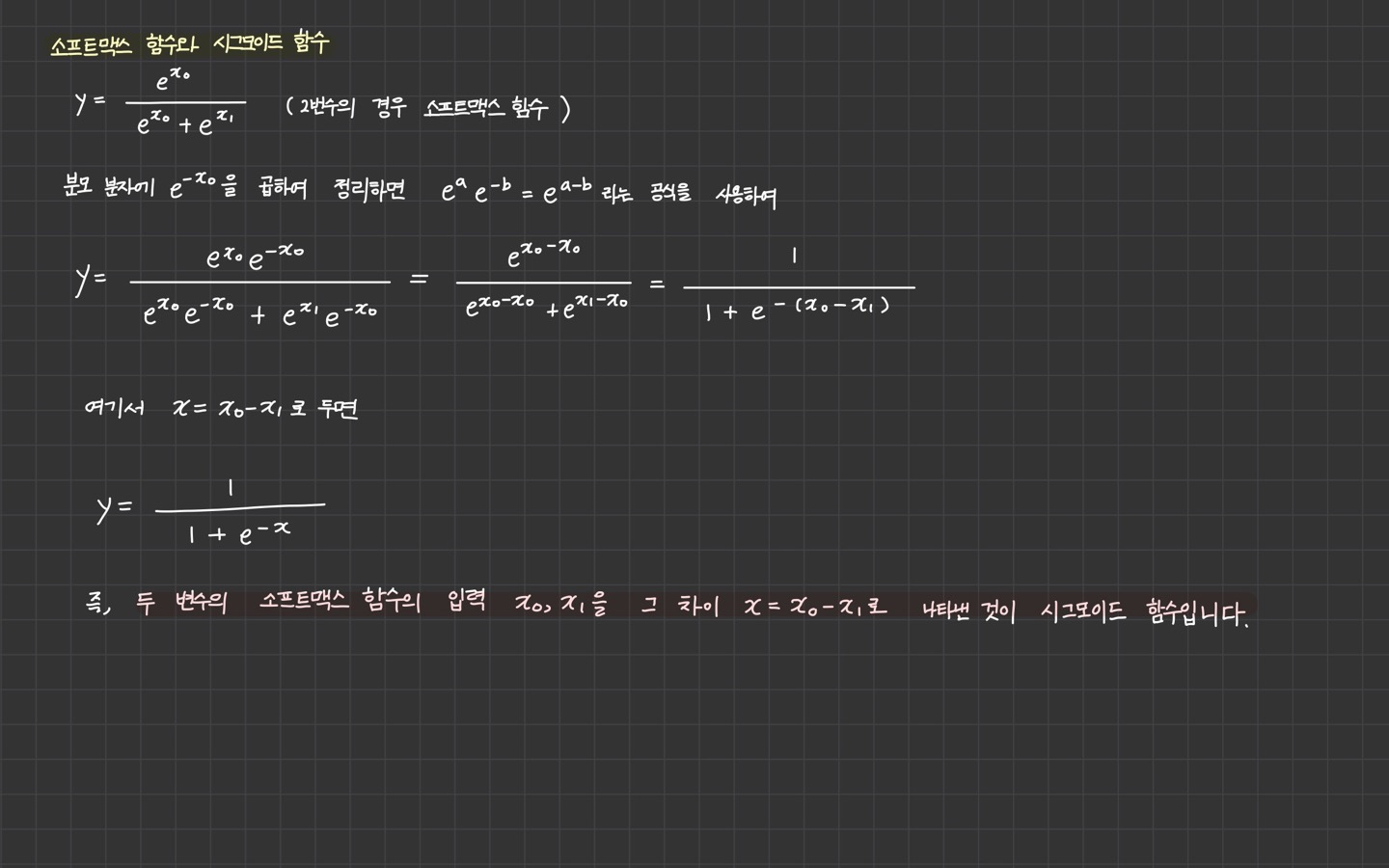
두 변수의 소프트맥스 함수의 입력 $x_0, x_1$을 그 차이 $x=x_0-x_1$로 나타낸 것이 시그모이드 함수입니다.

가우스 함수

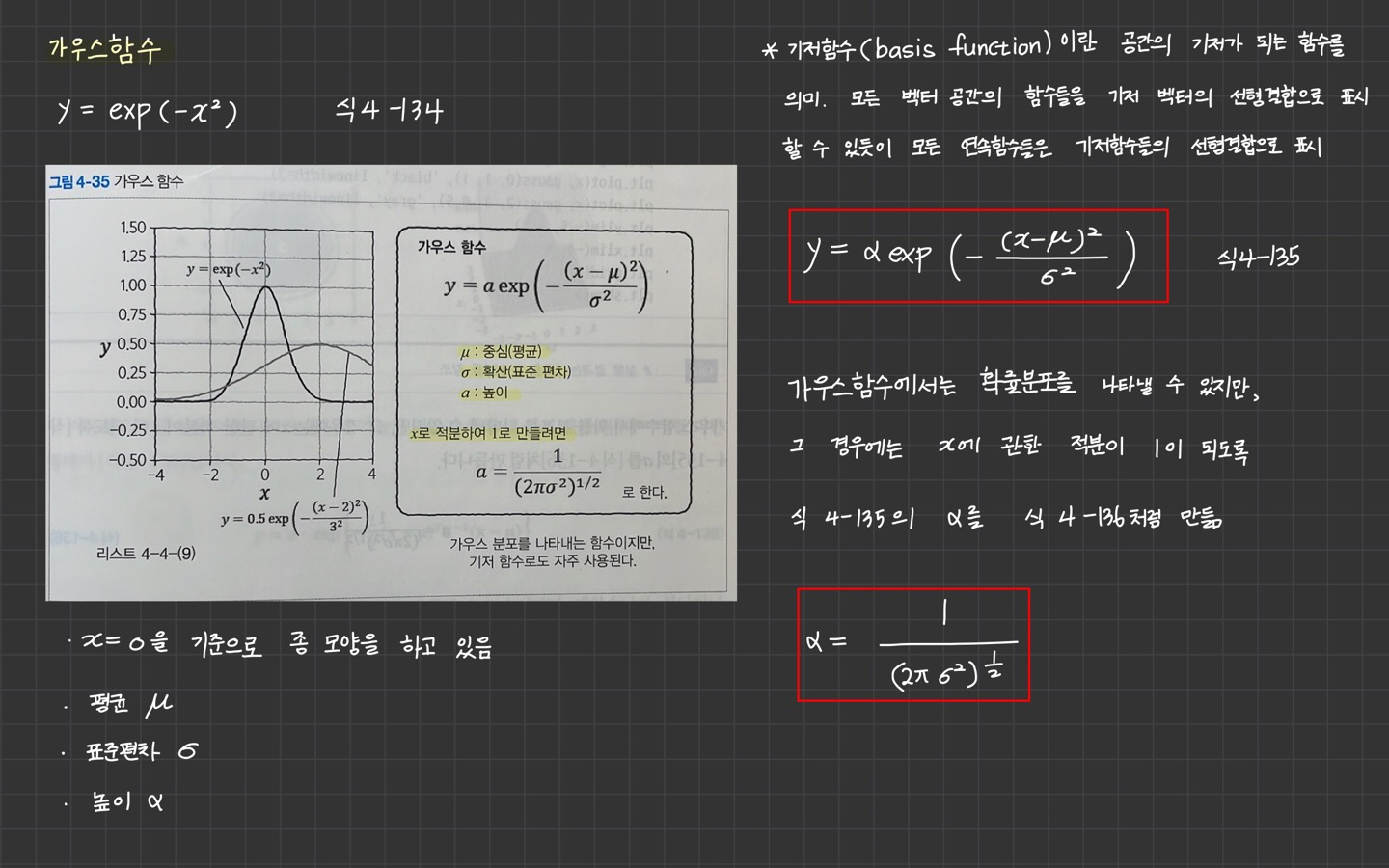
가우스 함수에 대한 식과 유도 과정은 조금 낯설었네요. 분명히 아는 정규분포의 개념인데도 말이죠~

2차원 가우스함수

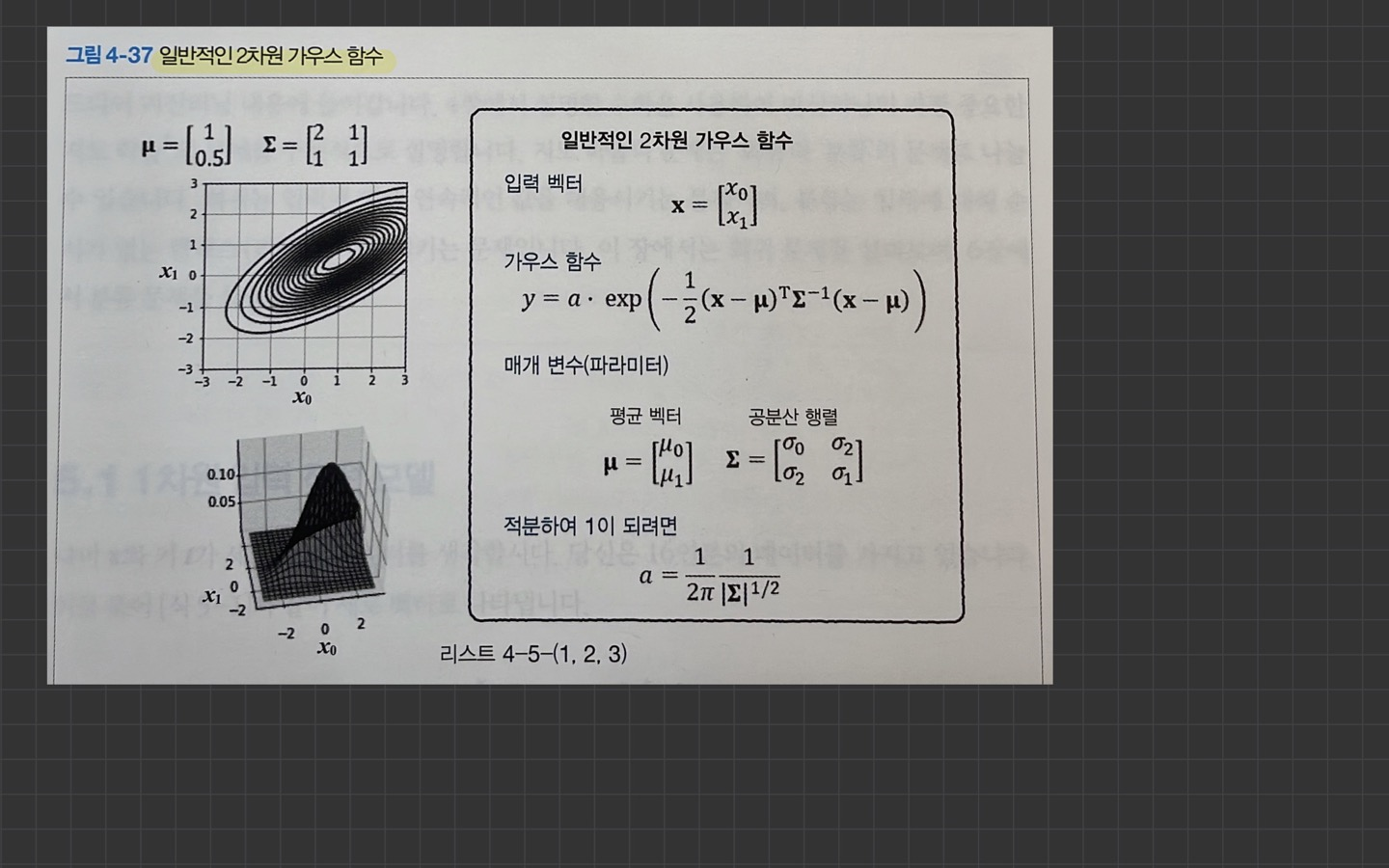
이상 기초 수학 정리를 마치겠습니다!

까먹을 때쯤 다시 보기 위하여!

그럼 모두 파이팅입니다.