[Linear Algebra] Orthogonal Vector and Subspace (직교 벡터와 부분공간)

Lecture 14 직교 벡터(Orthogonal Vector)와 부분 공간(Subspace)

저는 위 블로그를 참고하여 그대로 정리하였습니다. Gilbert Strang 교수의 Linear Algebra 강의를 정리한 포스팅입니다. 굉장히 정리가 잘 되어 있어서 강추합니다!

저는 단순히 내용을 그대로 따라 적으며 정리하였으며, 그냥 나중에 제가 복습할 때 보려는 용도로 포스팅합니다!

감사합니다.

Subspace 복습

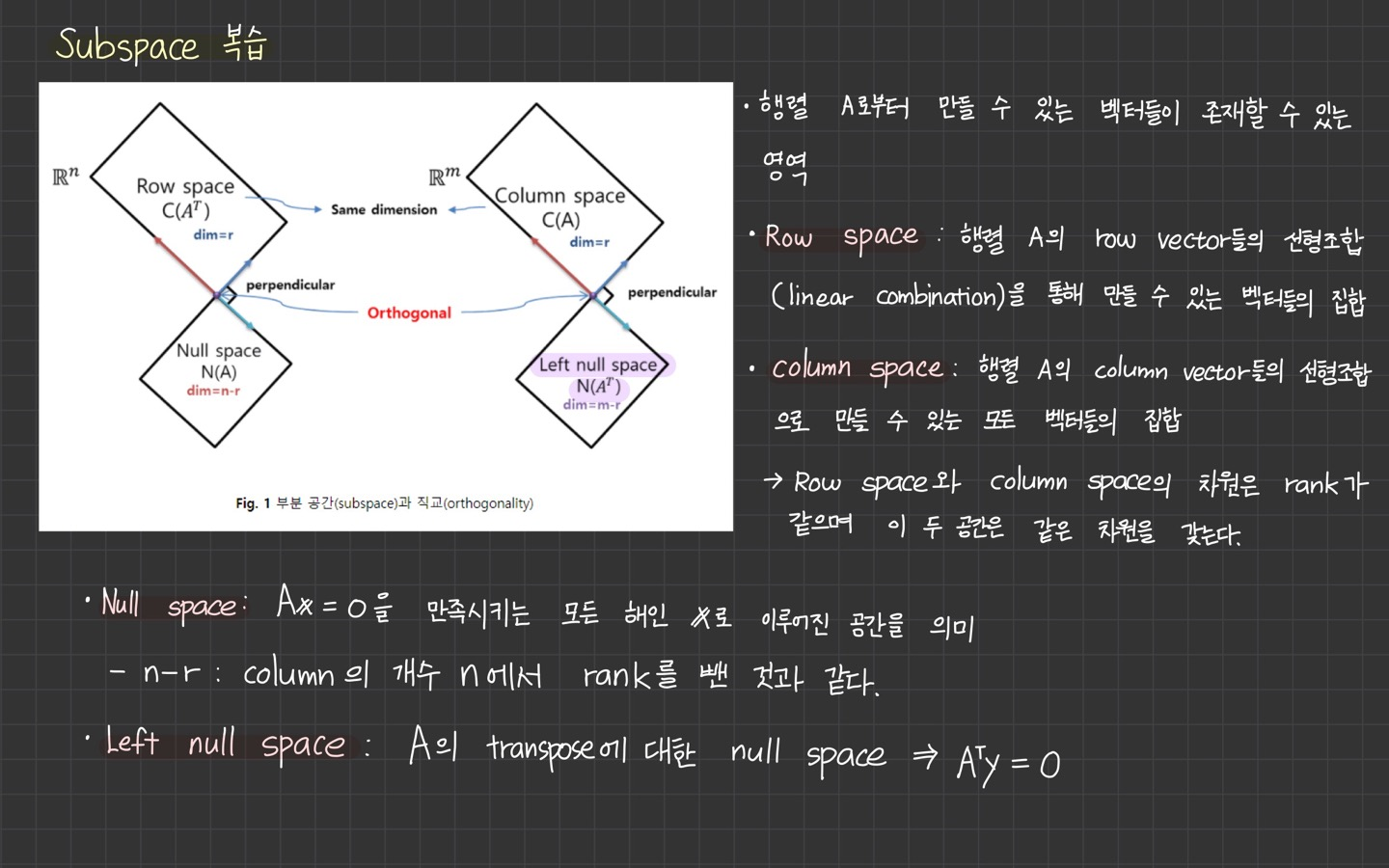
• Row space
• Column space
• Null Space
• Left null space

이제 하나씩 개념이 잡히고 있다.

직교 벡터(Orthogonal Vector)

• 직교는 다른 말로 쉽게 설명하면 수직이며, 두 벡터 사이의 각도가 90도를 이루는 것을 직교 벡터라고 한다.

내적(Dot product)

• ||·|| 벡터의 크기(norm)을 나타냄
• L2-norm을 사용한 식

선형대수적인 방법으로 풀이

$x^Tx + y^Ty = (x+y)^T(x+y)$

피타고라스의 직각삼각형에 대한 정리가 내적이란 개념과 어떻게 이어지는지...

Orthogonality of subspace

• S에 존재하는 모든 벡터가 T에 존재하는 모든 벡터와 직교해야 한다.
• 두 부분 공간이 만나는 점은 오직 원점에서 만나야 한다.

두 부분공간 S와 T가 부분공간이 되기 위해서

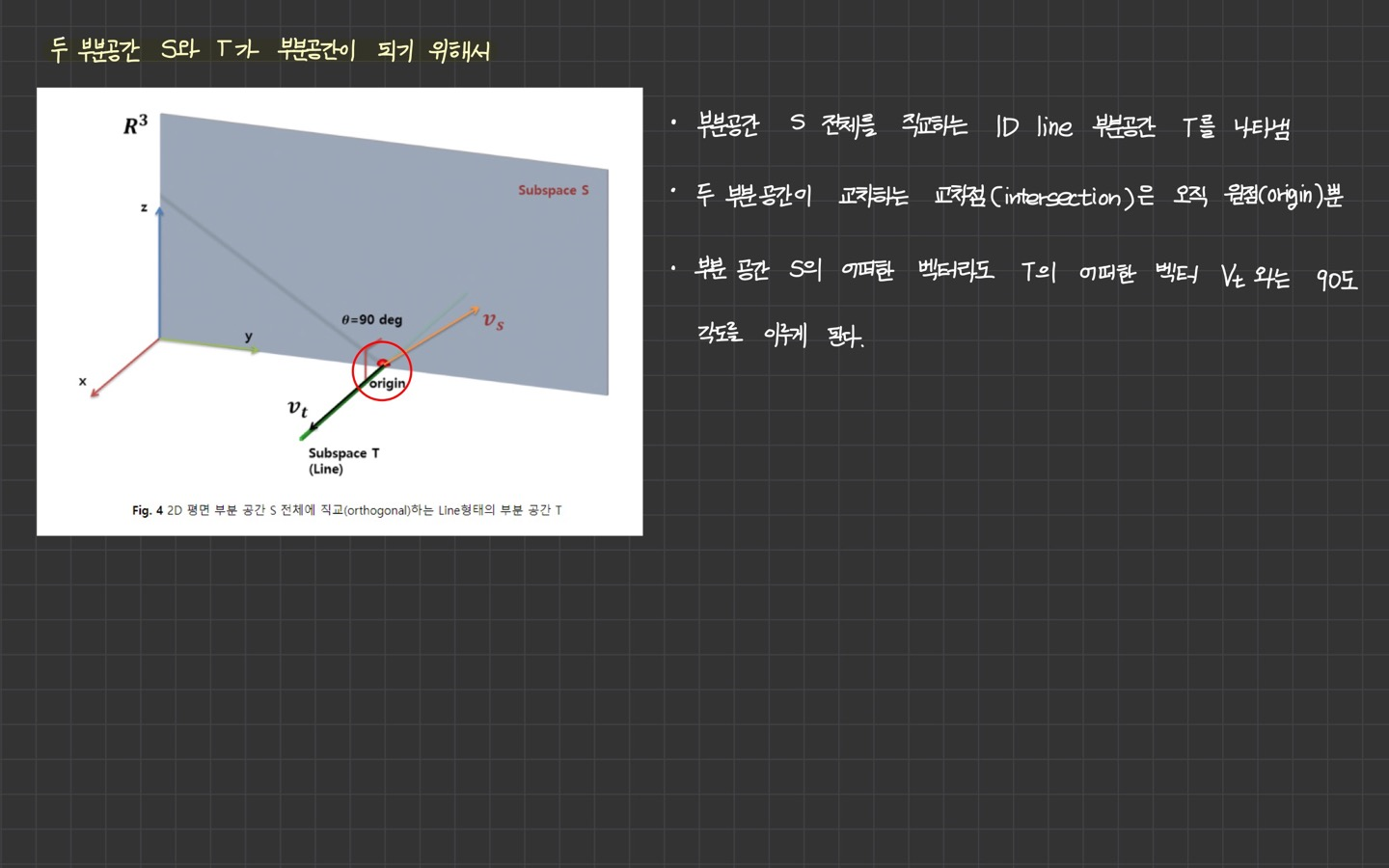
• 두 부분공간이 교차하는 교차점(intersection)은 오직 원점(origin) 뿐
• 부분 공간 $S$의 어떠한 벡터라도 $T$의 어떠한 벡터 $V_t$와는 90도 각도를 이루게 된다.

Orthogonality in row space and null space

• row space와 null space는 직교(orthogonal)한다는 것을 보여주는 과정

Row space와 null space 차원

Row space의 차원 + Null space의 차원 = $R_n$

Orthogonality in column space and left null space

Column space의 차원 + Left null space의 차원 = $R_m$

식(9)의 시각화

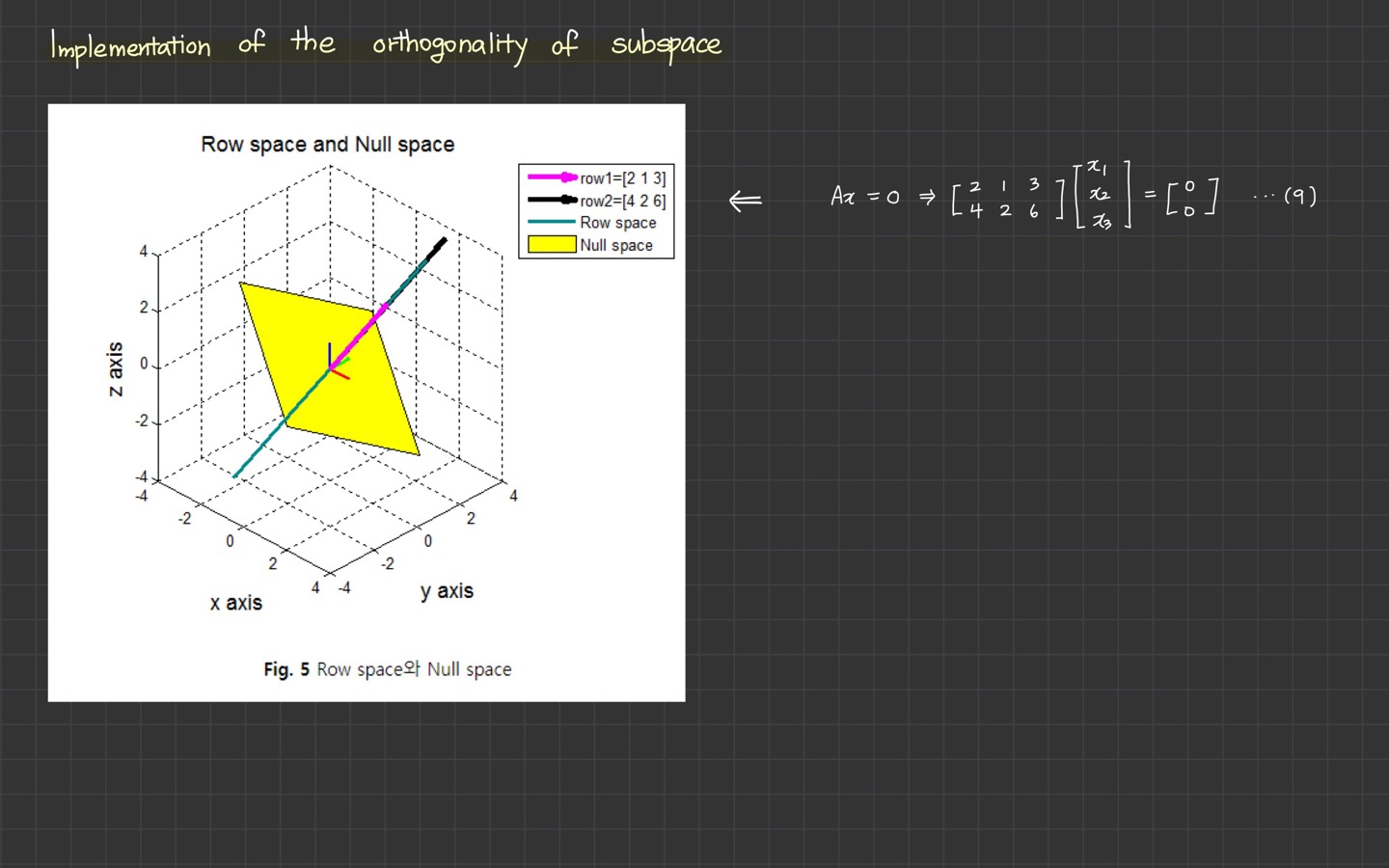
해당 그림을 통해 row space와 null space가 직교한다는 것을 직관적으로 이해할 수 있다.

여기까지 직교의 개념에 대해 정리해보았습니다.

다들 파이팅~!