[AI504] Class 05: Variational Autoencoders

✔️ MLP, Autoencoder가 2012년 이전에도 있던 old concept이라면 Variational Autoencoder는 2014년에 나온 concept이다.

✔️ 만약 다루기 힘든 inference problem이 있으면, variational inference나 MonteCarlo sampling에 의존할 수 있다. Variational Autoencoder는 variational inference에 heavily rely한다.

Generative Autoencoder

🔗 Generating new samples

• Perturb a known z
  • Diverse/novel samples를 만들어내지 못한다.
• Sample from a region
• 둘 다 잘 동작한다는 보장이 없다.

➡️ Autoencoder는 generative model로 적합하지는 않다. Autoencoder는 compress와 decompress algorithm이다. 따라서 적합한 generative model이 필요하다.

Variational Inference

Variational Inference는 posterior distribution을 estimate하는 것에 관한 것이다.

🔗 Posterior Distribution

• data X가 주어지고, unobserved (latent/hidden) variables Z가 있다.
  • Assumption : Z가 X를 결정한다.
  • Ex) Topic (Z) of newspaper articles (X)
    • Topic을 모르는채로 여러 다른 article을 보면 이들이 어떤 topic에 속해있는 것인지 궁금할 것이다.
  • Ex) Latent representations (Z) of MNIST images (X)
• 우리는 P(Z|X) 를 알고싶다.
  • 이것을 posterior distribution이라고 부른다.

• z는 prior distribution에서 온다.

• Bayesian principle을 사용한 true posterior distribution은 다루기 힘들다.
  

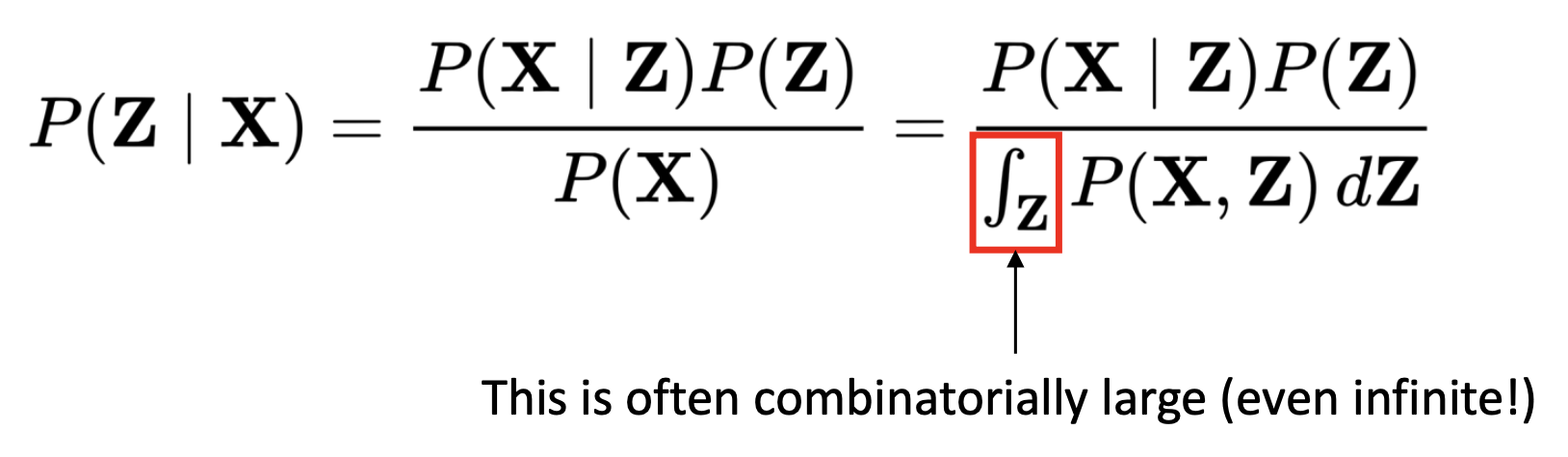
  • 분모 부분에서 integration이나 summation은 어렵다. Z가 continuous이거나 discrete여도 많은 개수가 있으면 모든 것을 integration 하는 것은 쉽지 않다. 그래서 posterior distribution P(Z|X)를 derive하는 것은 쉽지 않은 task이다.

💡 이를 handle하는 법 두가지

• z distribution에서 sampling하여 Monte Carlo Estimation을 한다.

  • 오래걸리고 쉽지 않다. Analytic하게 solve하기 어렵다.

• 대안으로, 최종 목표인 이 posterior distribution을 더 간단한 함수 Q로 approximate한다.
  

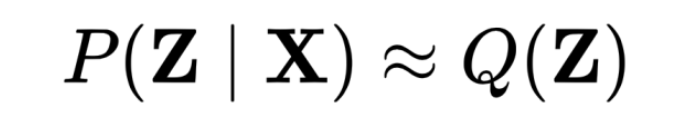
  • μ와 σ를 조정하여 이 gaussian distribution이 최대한 true positive distribution처럼 행동하길 바란다.

🔗 Learning Q(Z)

• Q(Z)가 P(Z|X)와 가능한 한 similar 하길 원하기 때문에, KL-Divergence를 사용하여 P로부터 Q가 얼마나 떨어져 있는가를 evaluate하고, Q를 update하여 KL-Divergence를 minimize하도록 한다.
  
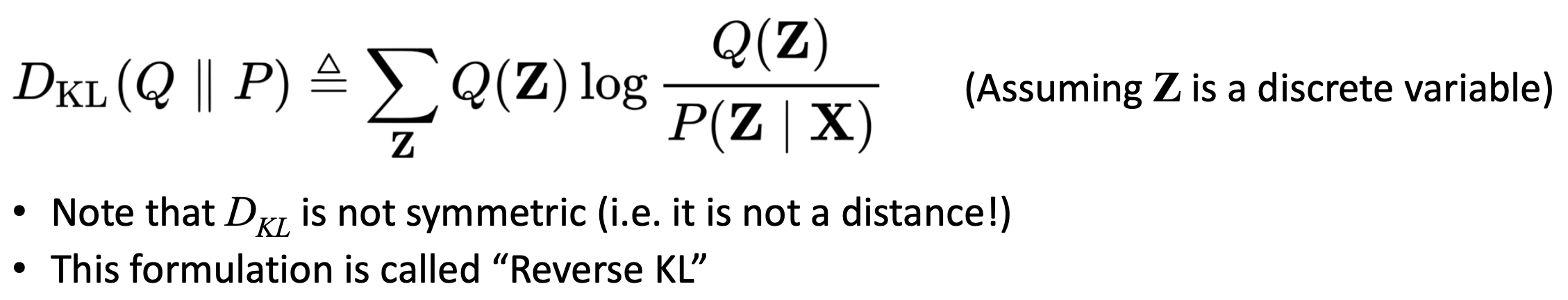
  • KL-Divergence는 보통 unknown distribution이 known distribution의 behavior를 흉내내도록 하지만 여기서는 반대로 간다.
  • D_KL(Q||P)는 variational inference를 위해 쓴다.
  • D_KL(P||Q)는 expectation maximization에 쓴다.

✔️ 식을 shuffle

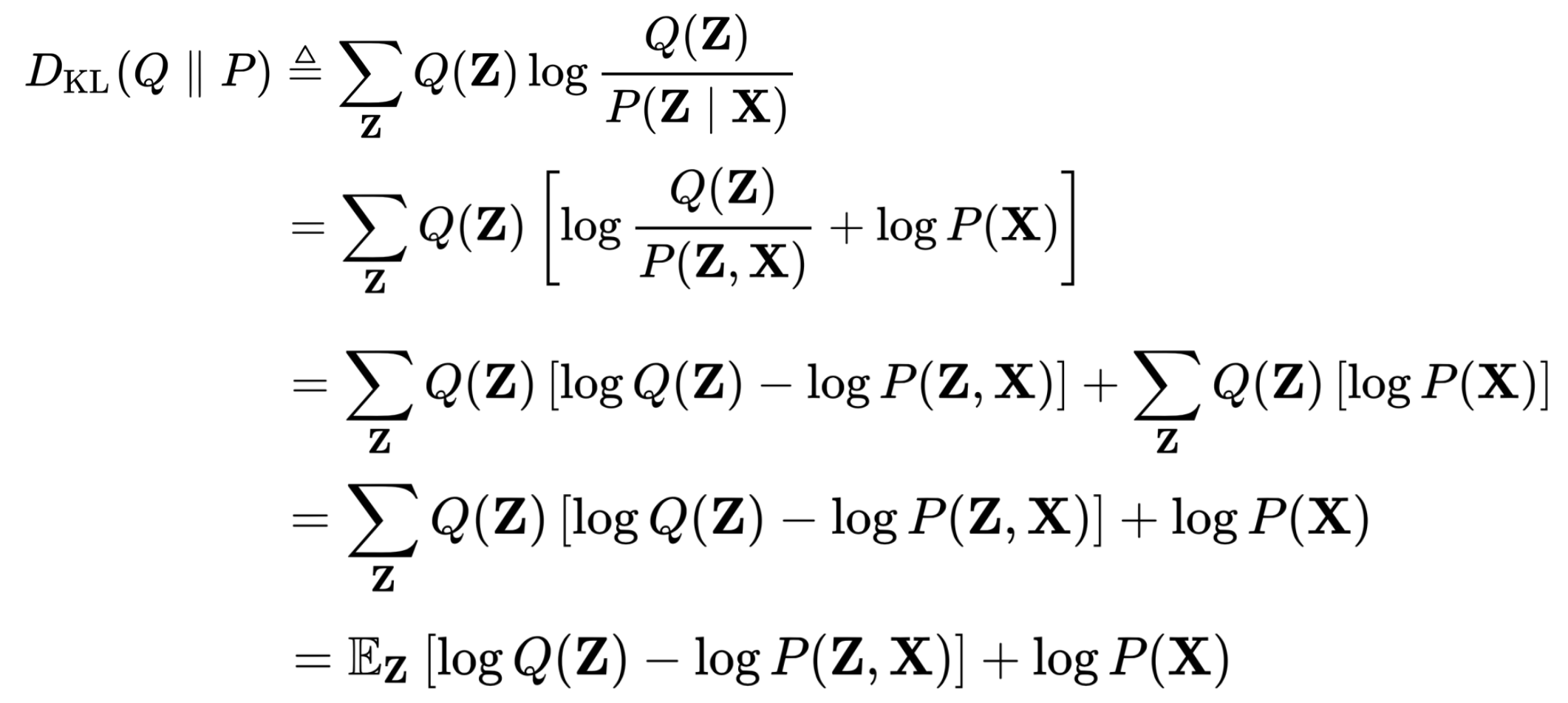
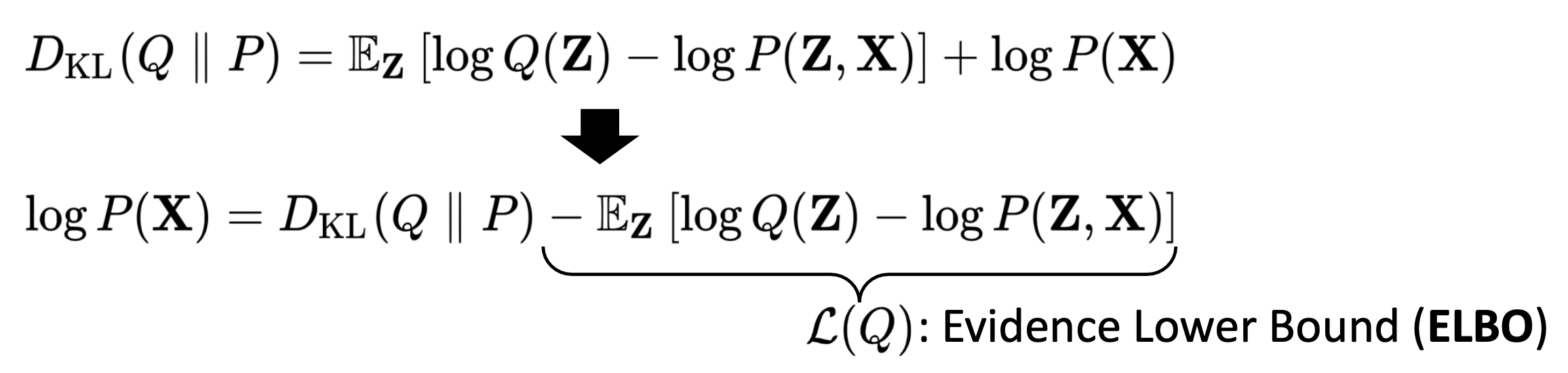
log p(X) = KL divergence term + ELBO term

⭐️ VI의 핵심 결론

• ELBO를 maximizing하면 D_KL을 minimizing하는 것으로 이어진다!

  • 이유 : log P(X)는 data distribution이고 data는 fix되어있기 때문에 log P(X)도 fix되어있다. constant이다.

  • ELBO를 maximize하는 것이 쉽다. 왜냐하면 P(X|Z)와 P(Z) 모두 우리가 아는 것이고, Q(Z)는 우리가 주로 다루기 쉬운 distribution이라고 이미 가정해놓았기 때문이다(주로 가우시안).
    log P(Z,X) = log P(X|Z) + log P(Z)

• Inference problem을 optimization problem으로 바꾸었다!

  • Q가 gaussian이라면, μ와 σ parameters를 optimize한다.
  • Opimization이 inference보다 쉽다.

ELBO means
D_KL은 음수가 될 수 없기 때문에 ELBO term은 log P(X)와 같거나 작아야한다. 그리고 P(X)는 evidence라고 불린다. 그래서 Evidence Lower Bound라고 불린다.
L(Q)는 "variational free energy"라고도 불린다.
왜냐하면 Entropy term을 가지고 있기 때문이다.
L(Q) = $E_Z$[logP(Z,X)] + H(Q) (H: Information Entropy)

Variational Autoencoder

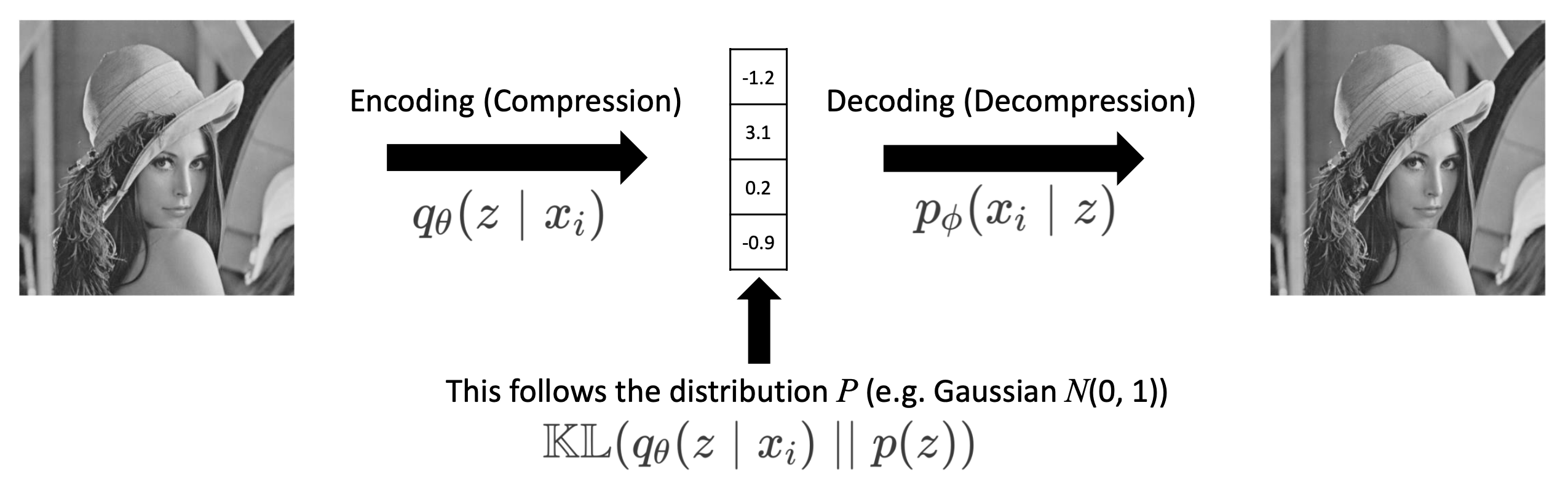
🔗 Objective

• x를 P(Z|X)를 따르는 z로 compress한다.
• z를 decompress하여 x로 reconstruct한다.

🔗 AE에서 추가된 것 한가지

• Latent space z가 특정 distribution(usually Gaussian)을 따르길 바란다.

⭐️ Motivation

• Latent space에 certain structure를 넣으면, 그 structure latent space에서 sampling하여 realistic sample을 얻을 수 있을 것이다.

➡️ Data distribution P(X)을 probability distribution P(Z)로 mapping한다. 이것이 Encoder이다.
➡️ P(Z)에서 z를 sample하여 x로 전환한다.

🔗 VAE Loss

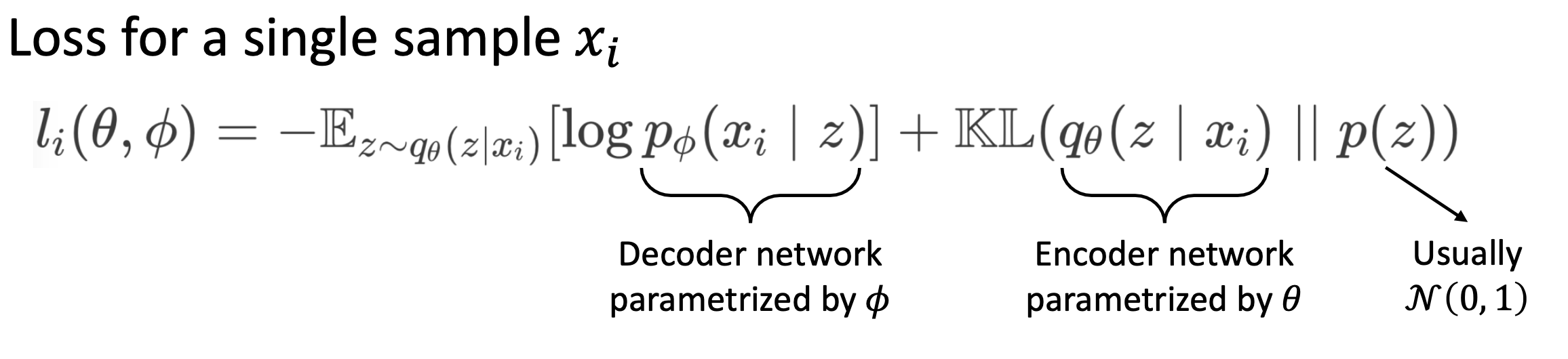
• Reconstruction loss
  • $x_i$가 주어졌을 때 encoder를 통해 z에 대한 distribution을 얻는다. 그리고 이 distribution에서 아무 z를 가져와 그 z를 decoder에 넣으면 $x_i$'을 얻는다. $p_Φ$($x_i$|z)를 높이는 것이 reconstruct term이다.
• Regularization term

Compression/Decompression algorithm 측면에서는 VAE가 vanilla AE보다 열악할 수 있다(decrease freedom of model). 하지만 generate new sample에 관해서는 더 realistic한 sample을 generate할 것이다.

자, 이제 probabiliy 관점에서 생각해보자.
우리는 posterior distribution P(Z|X)를 infer하고 싶다. Image가 주어졌을 때 latent distribution or latent variable z를 알고 싶다.

🔗 VAE Posterior Distribution

• P(Z|X)는 다루기 힘들기 때문에, variational inference를 사용한다.
  

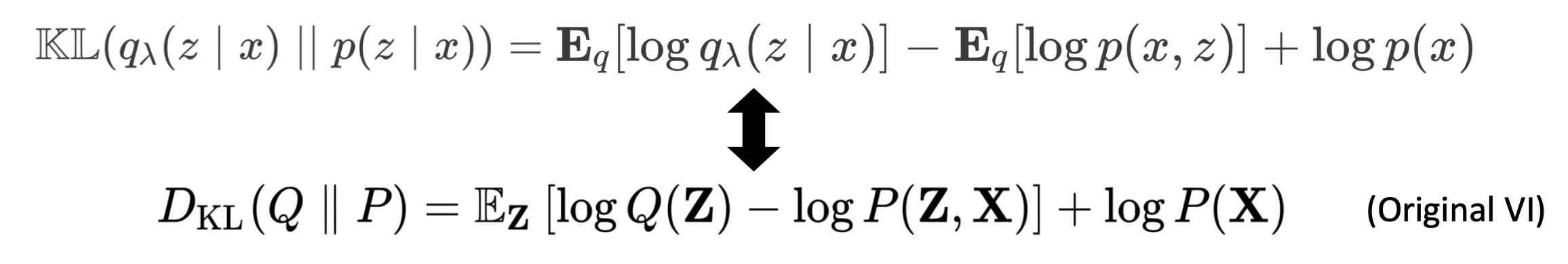
  • True P(Z|X)를 모르기 때문에, $q_λ$(z|x)로 estimate한다. 이것이 encoder가 된다.

• z는 $x_i$에 의해 결정되기 때문에 q(z)말고 $q_λ$(z|x)를 쓴다.

  • λ는 gaussian q에서의 (μ, σ)이다.
  • $x_i$를 Encoder function에 넣으면 $μ_i$와 $σ_i$를 generate한다. 이 $μ_i$와 $σ_i$로 gaussian distribution을 만들 수 있다. 그리고 $z_i$가 N($μ_i$, $σ_i$) distribution에서 나온다. $z_i$ ~ N($μ_i$, $σ_i$)

• 이런 encoder를 학습하고 싶다.
  

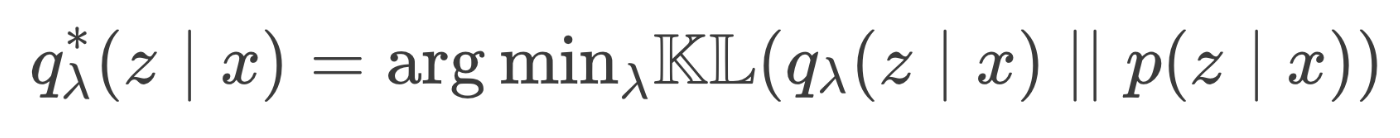
이를 통해 나온 새로운 ELBO term에 대해 알아보자.

🔗 The new ELBO term

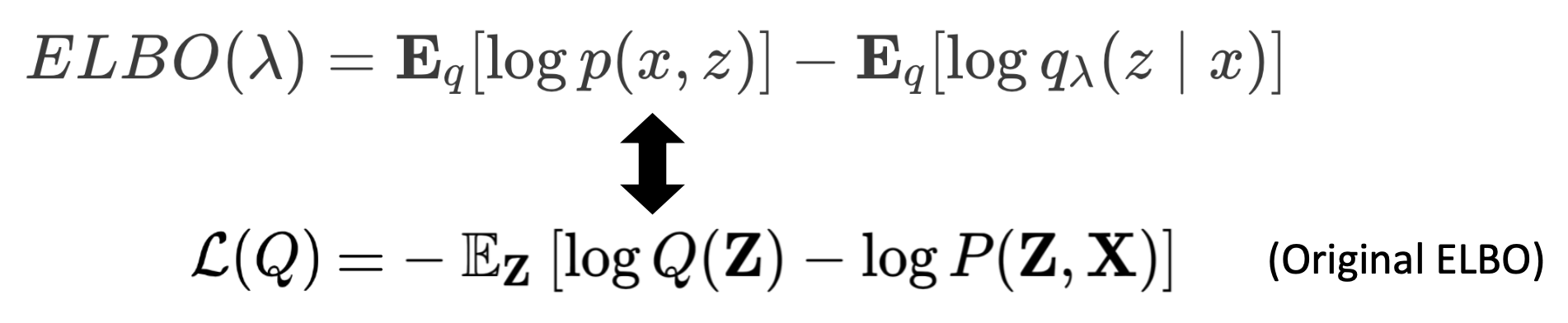
• ELBO term for each $x_i$
  
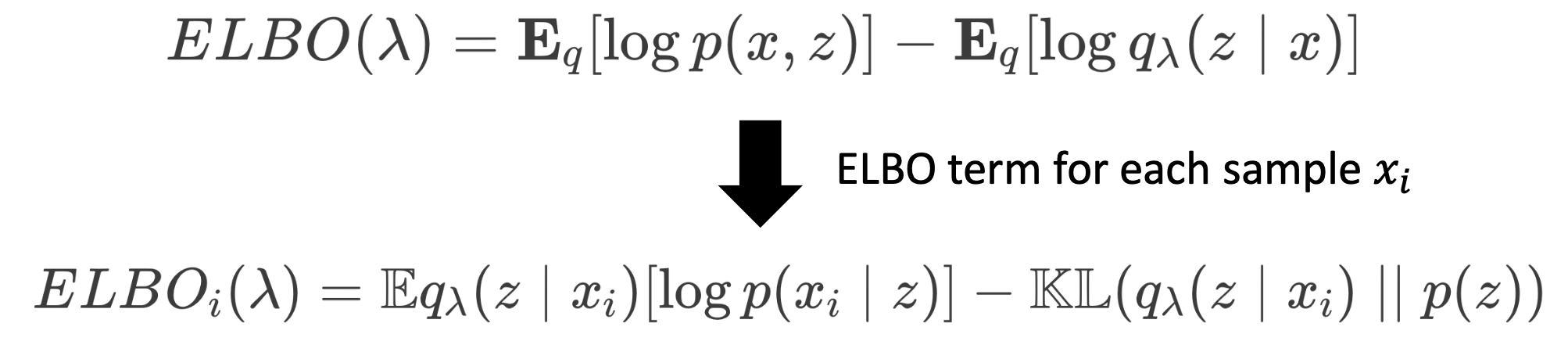
  • Approximate posterior q with θ
  • Likelihood p with Φ
  • θ와 Φ parameters를 update하여 ELBO term을 maximize해야한다. 이것이 D_KL을 minimize한 것으로 이어진다.

⭐️ VAE 안에 VI nature가 있다고 말하는 이유

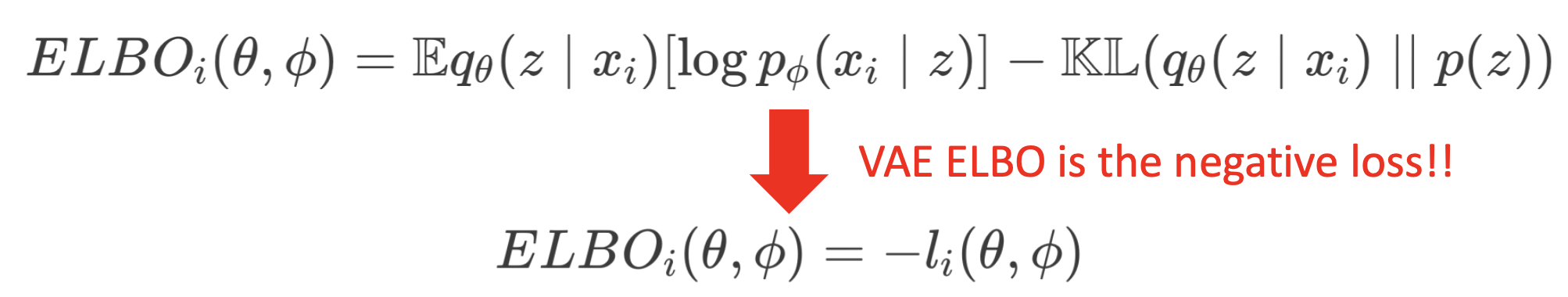
2개의 매우 다른 관점에서 시작하였는데, 결과가 같다.

1. AutoEncoder에서 시작하여 regularization term을 추가하여 VAE loss term 결과를 얻었다.
2. Purely probability 관점에서 시작하였다. P(Z|X)를 infer하고 싶었고 그 결과가 ELBO term으로 이어졌다.

➡️ ELBO를 maximizing하는 것은 loss를 minimizing하는 것과 같다!

ELBO에서 모든 term이 우리가 아는 것이다. 그래서 VAE를 training할 수 있다.

• How to maximize ELBO
  • θ를 학습하여 encoder network를 update하고, Φ를 학습하여 decoder network를 update한다. 이 두 parameters를 둘 다 update한다.

이렇게 하여 VAE를 하나의 reguralization term을 추가하는 것 뿐만 아니라 어떻게 maximizing ELBO로 해석하는지까지 알아보았다.

Reference

• AI504: Programming for AI Lecture at KAIST AI