Graphs
🔗 Graph Data Examples
-
Friends Network
-
Social Network Analysis
-
PageRank
-
Chemical structures
-
Knowledge Base
-
Sequences : special case of graph (i.e. directed chains)

-
Images : speical case of graph (i.e. undirected grids)
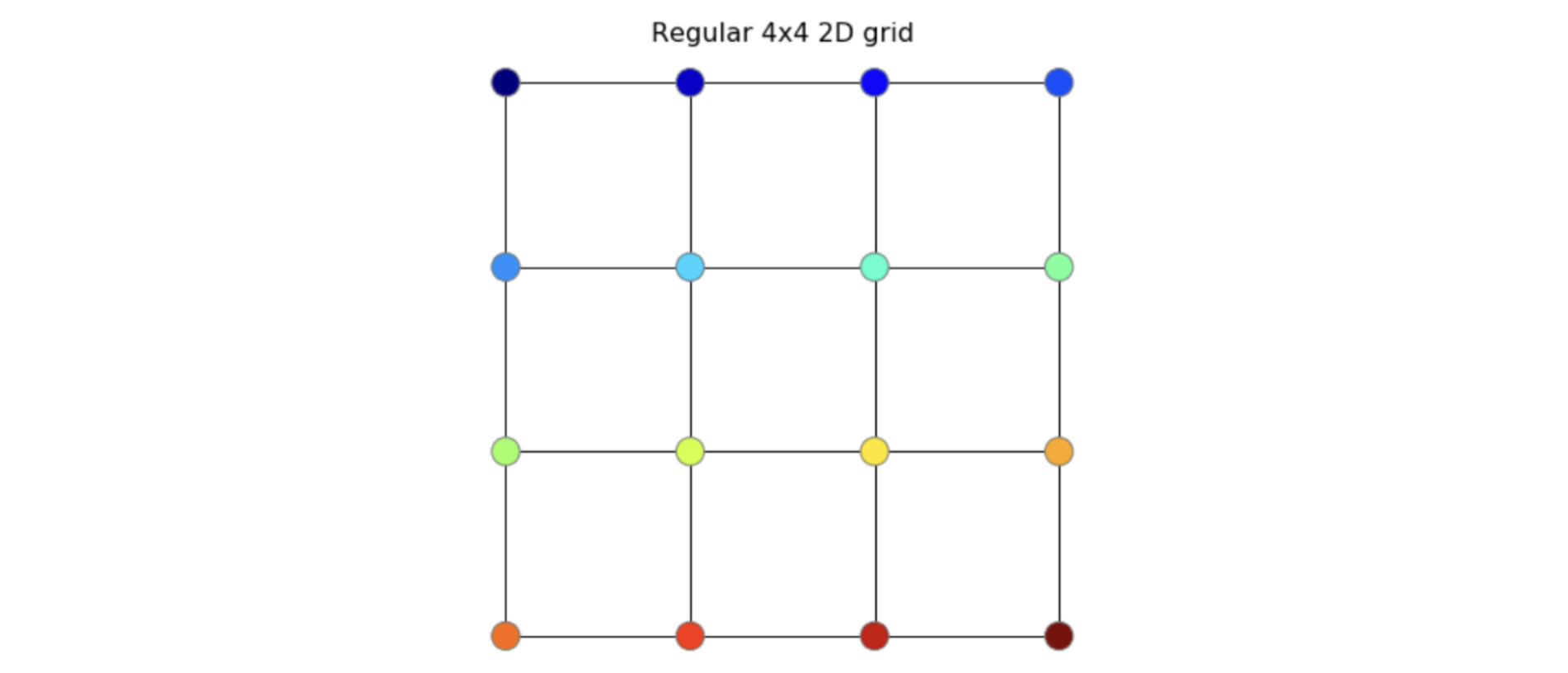
Graph Convolution
🔗 Graph Representation
- Graph를 fixed size vector에 embed하고 싶다.
- |V| nodes and |E| edges -> ❓ -> |V| embeddings (and |E| embeddings)
- 각 node를 represent하는 |V|개의 embeddings를 얻고 싶다.
- 주로 node에 대해서만 신경쓴다.
🔗 Why not ConvNet?
- Convolution filter는 같은 수의 neighbors를 가정한다.
- ConvNet은 single main pixel에 focusing하여 neighbor pixel values를 모으고 이들을 weight summing한다. 그리고 다음 main target으로 이동하는 식으로 image의 끝에 도착할 때까지 반복한다.
- 하지만 graph는 node당 neighbor의 수가 고정되어 있지 않다. 그리고 그런 order도 없다.
그래도 ConvNet filters의 core principle인 local neighbors로부터 features를 aggregate하는 것을 graph에 적용할 수 있다.
🔗 Graph Convolution Principle

🔗 Graph Convolution Equation
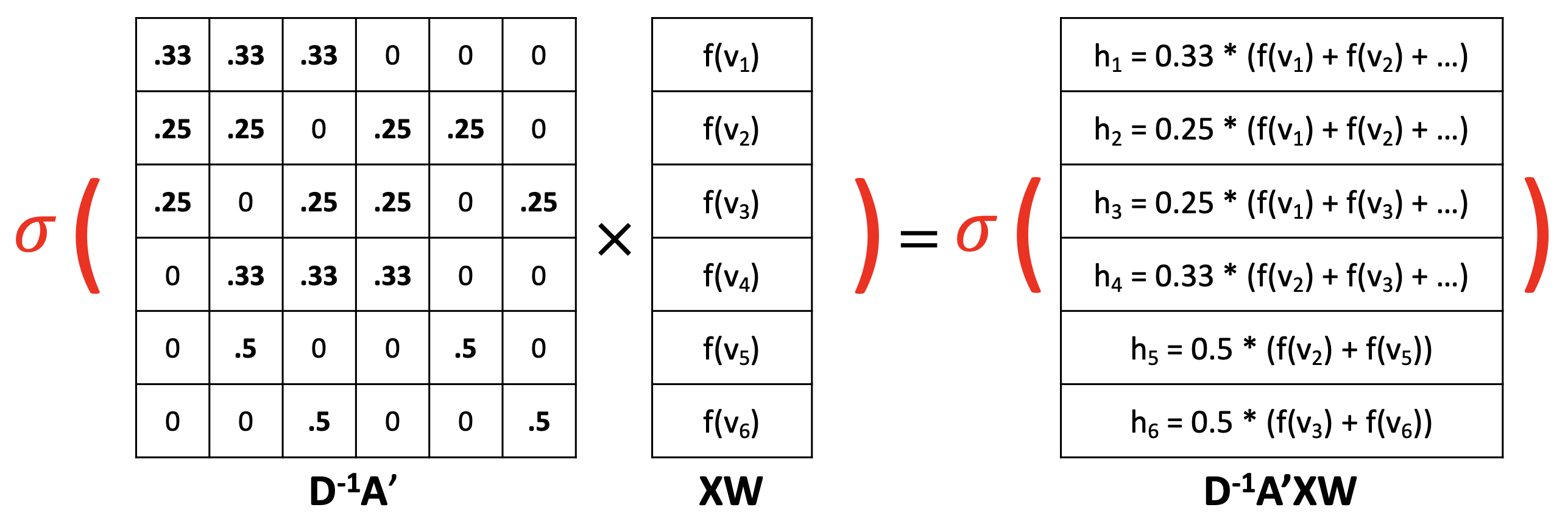
-
A: Adjacency matrix
- matrix를 이용하여 graph를 나타내는 방법
- row와 column의 개수가 graph의 node의 개수와 같고, matrix에서 각 cell의 value는 connection 여부를 나타내는 binary(0 or 1)값이다.
-
X : Node index
-
W : Node embedding vector
- = look-up table for node
① AXW : neighbor aggregation
② New A' = A + I
- I : Identity matrix
- Combination (neighbor aggregation + self-embedding)
- Self-loop/self-connection을 추가한다.
③ A'XW : neighbor aggregation과 combination을 수행
- Combination function g가 simple summation인 것.
- A'XW는 node representations H가 될 수 있다.
④ D^(-1)A' : Normalized adjacency matrix
- D : Degree matrix
- 각 node의 edge의 개수로 이루어진 diagonal matrix
- Normalization step
- 이렇게 normalize하기 않으면 node features의 scale이 neighbor의 개수에 따라 상당히 달라진다.
⑤ 지금까지는 모두 linear operation이므로 non-linearity를 추가한다.
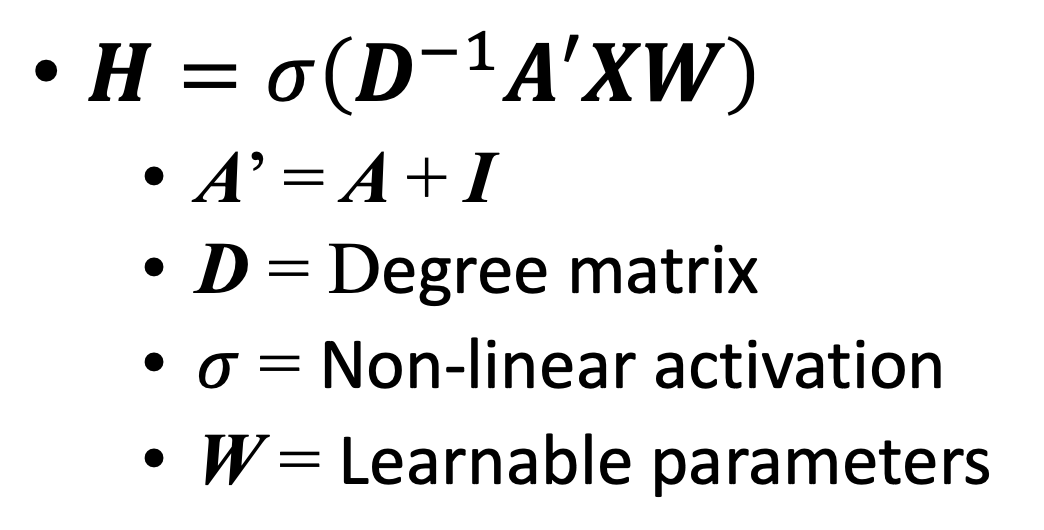
- 총 1개의 learnable parameter : W look-up table
- The simplest graph neural network
✔️ Aggregating neighbors just 1-hop away (direct neighbors)
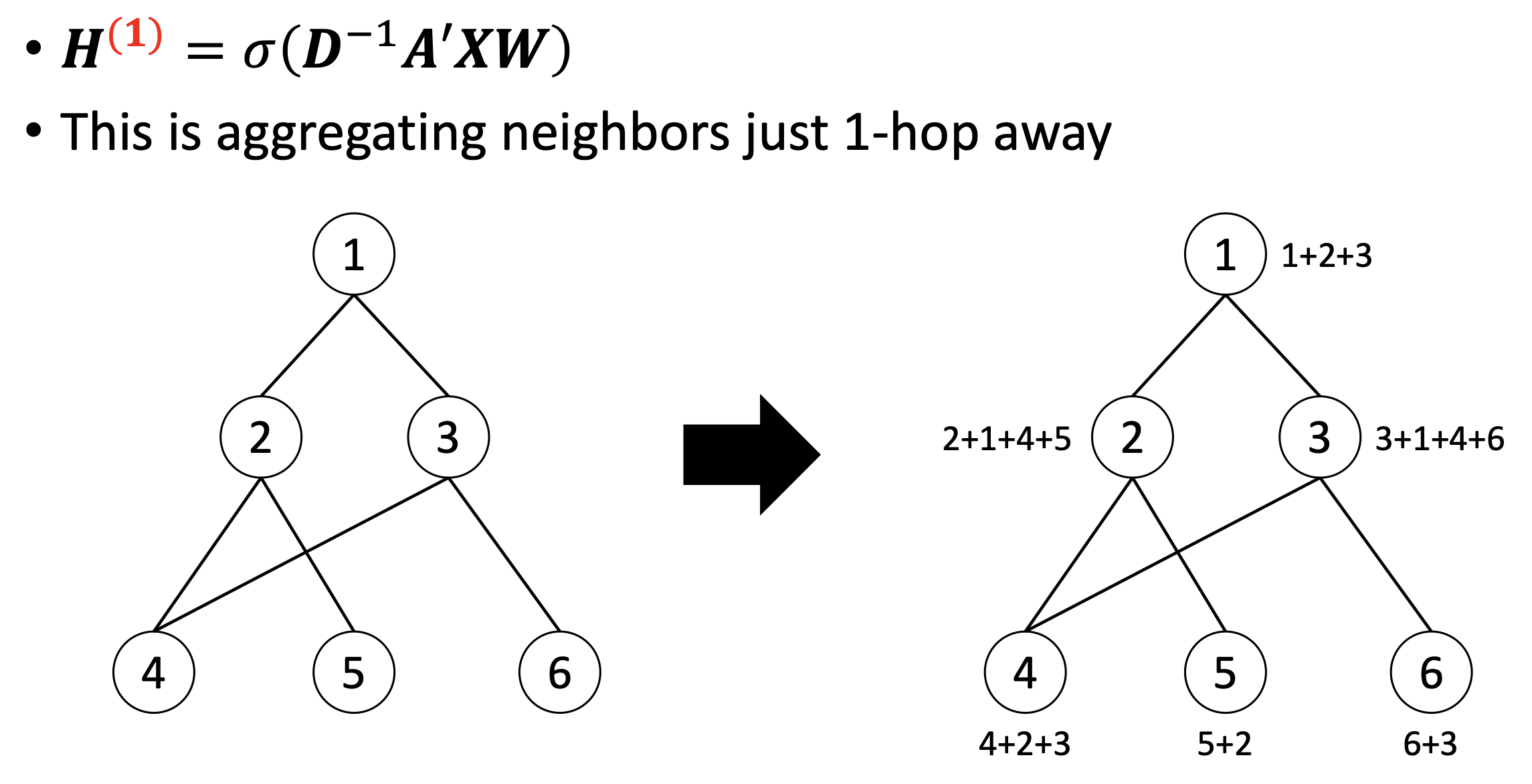
✔️ Aggregating neighbors 2-hops away
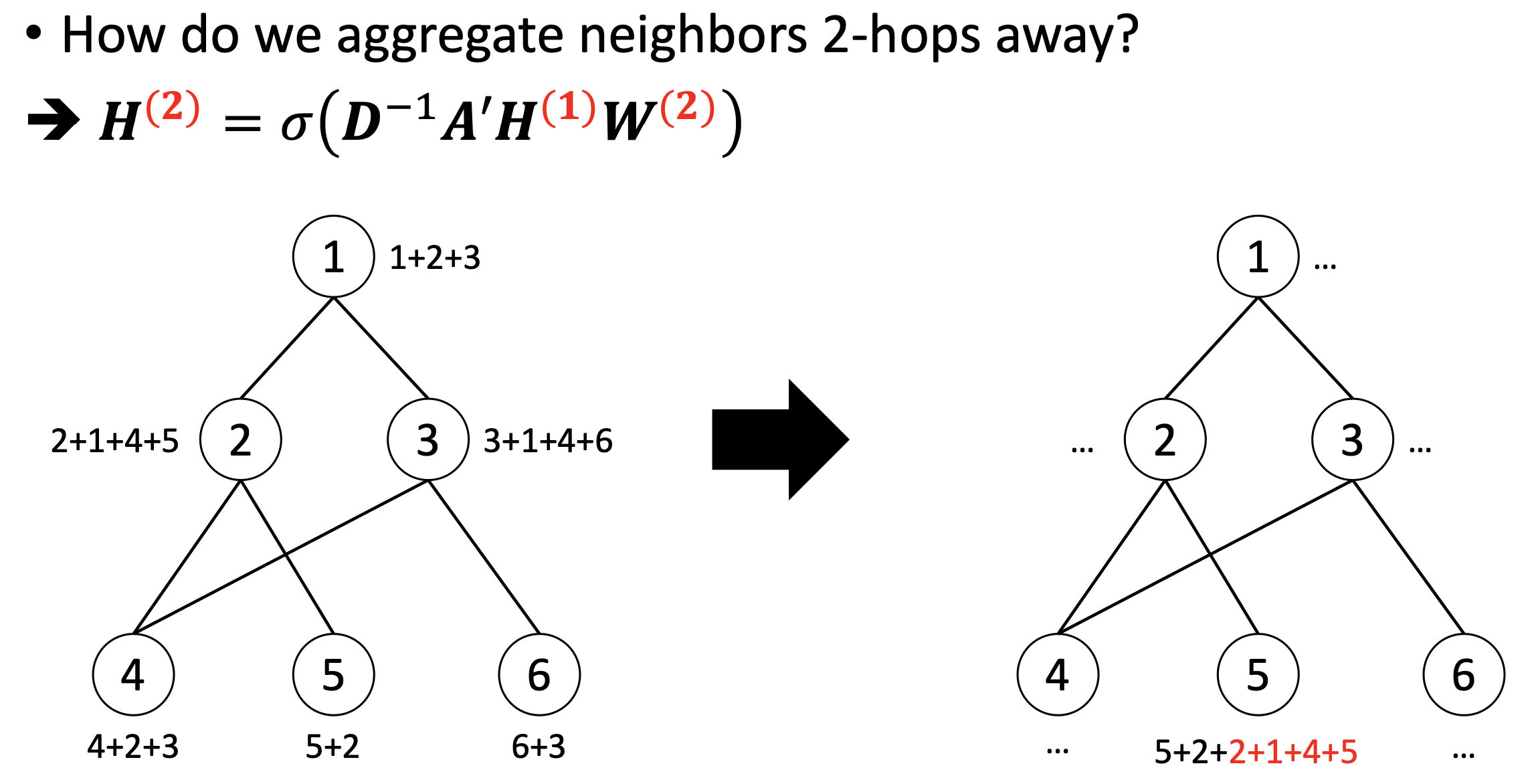
✔️ Aggregating neighbors k-hops away
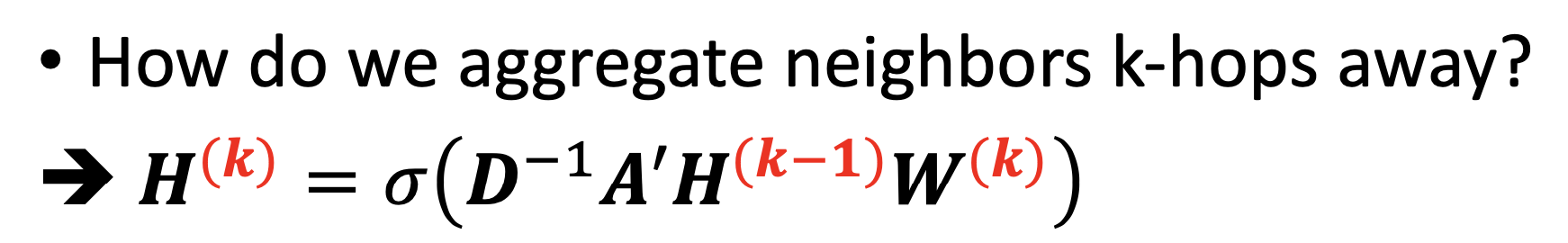
- Graph convolution layer를 쌓는다.
- 각 graph convolution layer는 1개의 learnable look-up matrix를 필요로 한다.
- local neighbors 정보를 모으는 것이 목적이므로 보통 2~3개 정도의 적은 개수의 layer만 쌓는다.
이런 simplest graph neural network와 그 variation들을 통틀어 Graph Neural Networks(GNN)라고 부른다.
Graph Neural Networks & Transformer
🔗 Self-attention
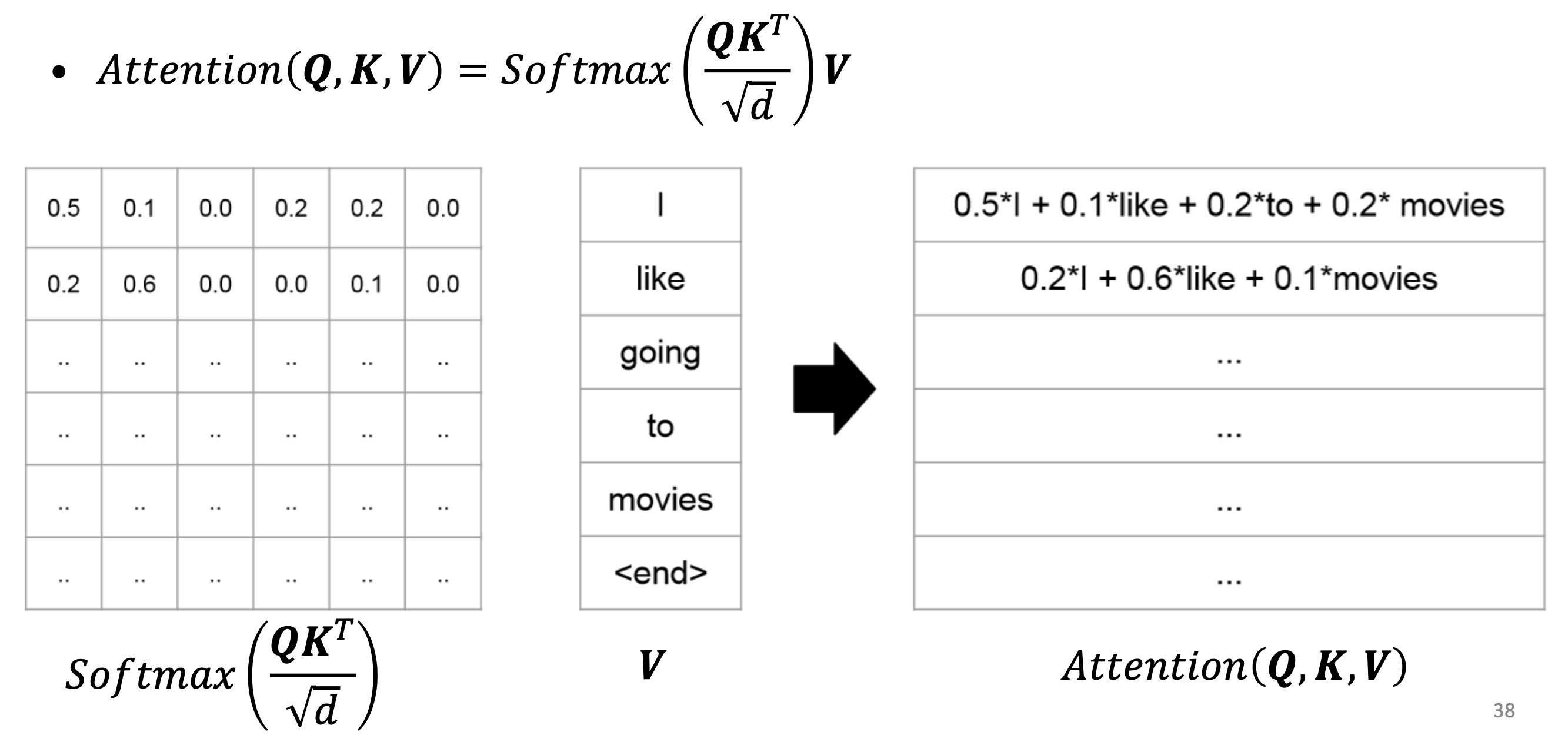
-
Self-attention의 기본이 되는 전제는 모든 것이 다른 모든 것과 연결되어 있다는 것이다. 즉, fully connected graph인 것이다.
-
실제로는 0 weight의 edge는 없다.
🔗 Graph Convolution
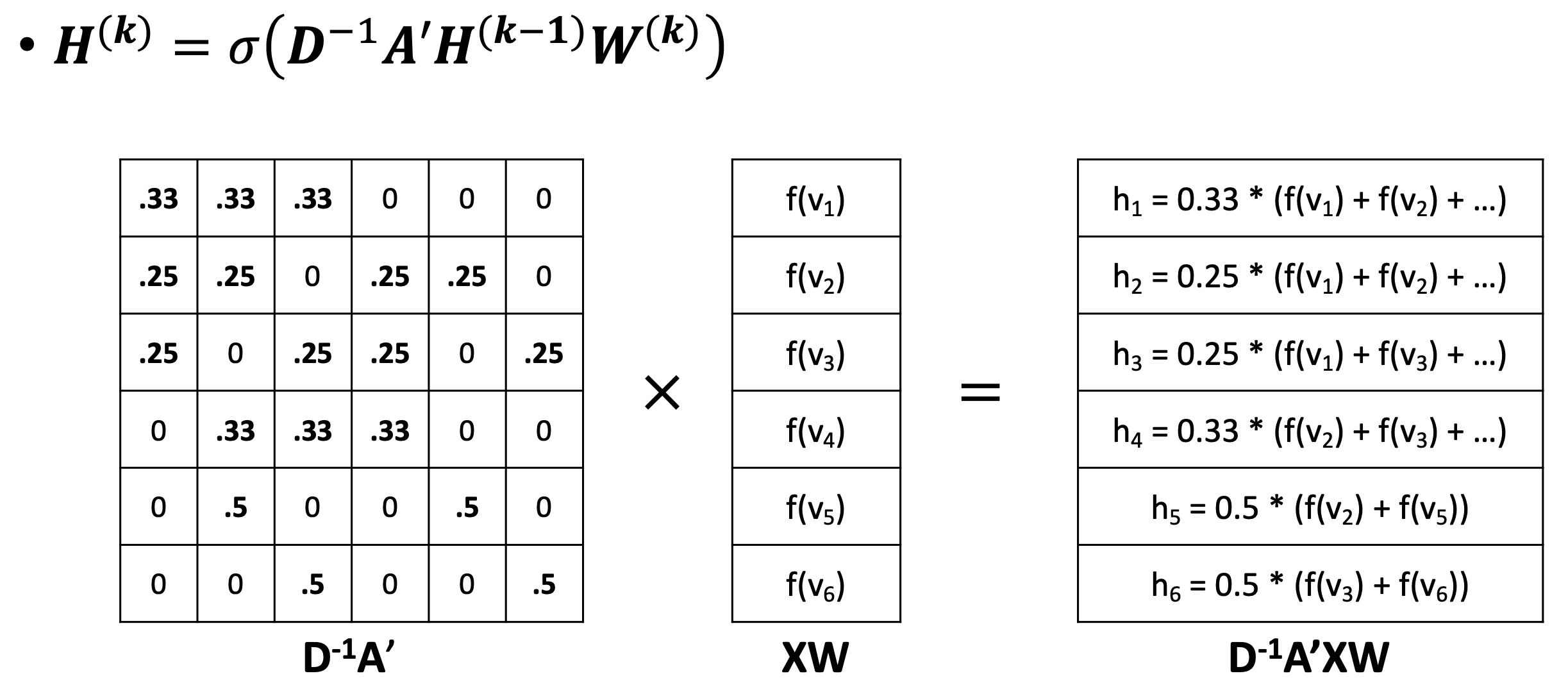
- Self-attention과 비교해보면 완전히 같은 모양이다. 둘 다 row-wise sum이 1이고 마지막에는 weight sum을 한다.
- 한 가지 다른 점
- Self-attention에서 attention matrix는 data로부터 학습하는 learnable parameter이다.
- Graph convolution에서 normalized Normalized adjacency matrix는 data로부터 predefine된다.
🔗 Transformer & Graph Networks

-
Graph Networks : 그냥 non-linear activation 말고 MLP를 통해 power increase
- General form of graph neural network
-
Transformer : Add & Normalization을 빼고 생각하면 self-attention -> feed forward network로 생각할 수 있다.
-
Adjacency matrix와 self-attention은 1대1 대응된다.
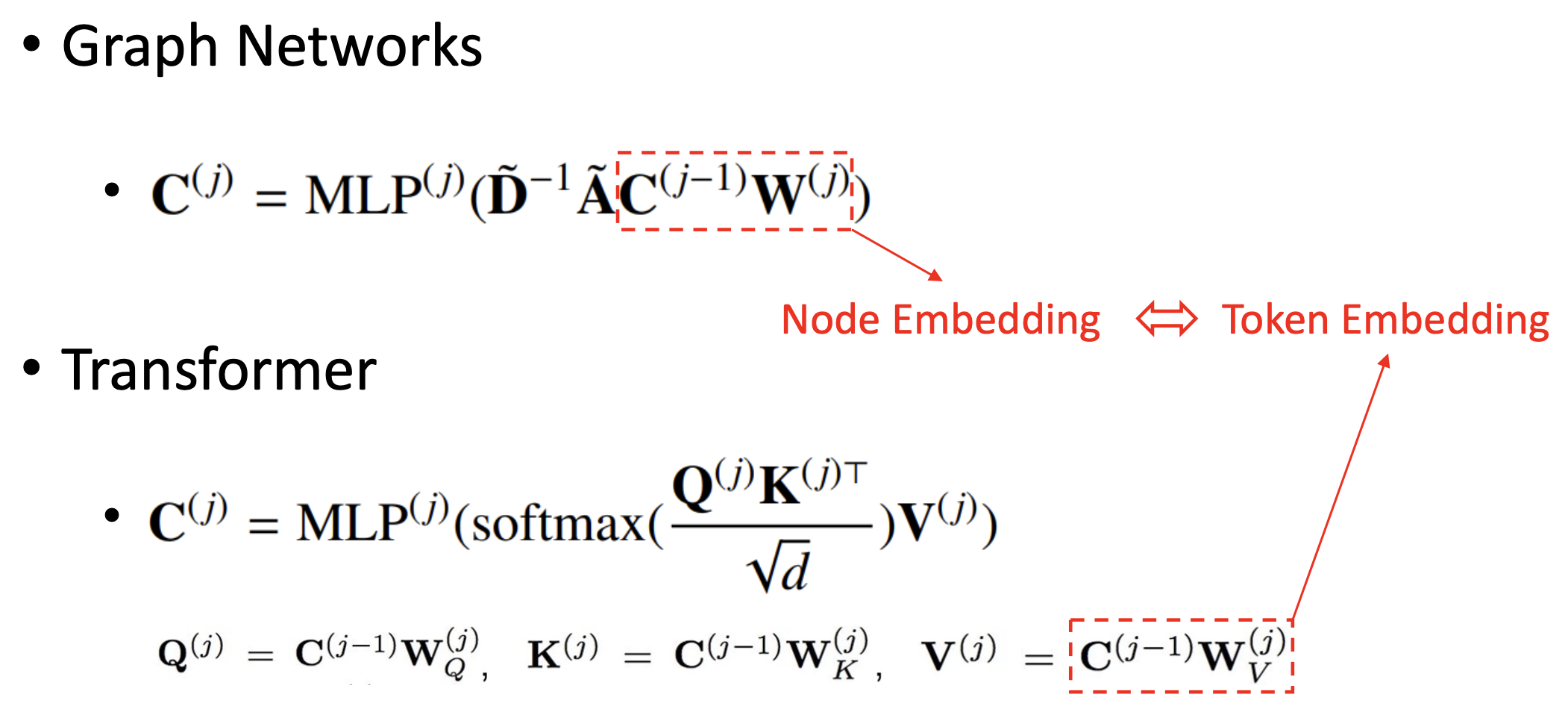
- Node Embedding과 Token Embedding도 1대1 대응된다.
- Self-attention에는 두 개의 learnable parameters 와 가 더 있다.
🔗 Self-Attention & Graph Convolution
-
Self-attention
- Graph structure/topology를 모를 때 쓸 수 있다.
- Fully-connected graph라고 가정하고 training을 통해 edge weights를 학습한다.
- |V| number of word embeddings를 data-driven fashion으로 학습한다.
-
Graph convolution
- Graph structure/topology를 알 때 쓸 수 있다. Graph structure에 대한 사전 지식을 D^(-1)A'에 반영한다.
- |V| number of word embeddings를 fixed adjacency matrix를 기반으로 학습한다.
-
Hybrid version
- Partial graph structure/topology를 알 때 쓸 수 있다.
- Graph Attention Network : graph topology를 아는 데 edge마다 다른 weight를 주고 싶을 때 쓸 수 있다.
- Negative infinity mask를 non-connnected edges를 mask하는 데 쓰고 connected edges에 대해서만 attention을 쓴다.
- 이를 통해 오직 connected edges에 대해서만 attention을 기반으로 edge weights를 dynamic하게 학습할 수 있다.
- Graph Convolutional Transformer
🔗 Chemical Structures
- AlphaFold : Euoformer라는 transformer를 사용하여, 아미노산 서열로부터 protein의 graphical 3D structure를 예측하였다.
- COVID-19 : BERT를 사용하여 chemical compounds의 3D graphical shape를 예측하고 COVID-19에 대한 효과를 예측하였다.
➡️ 매우 많은 양의 data가 있다면, 많은 Graph Neural Networks를 Self-attention으로 대체할 수 있다.
Reference
- AI504: Programming for AI Lecture at KAIST AI
