[Paper Review] ResNet

Abstract

문제
Deeper neural networks는 train하기 어렵다

해결 : Deep residual learning framework

• Adress degradation problem : network depth가 증가함에 따라 정확도가 포화 상태가 된 다음 급격히 저하된다.
• 이전에 사용된 것보다 훨씬 깊은 네트워크의 훈련을 용이하게 하기 위해 residual learning framework를 제시한다.
• 이러한 residual network가 optimize하기 더 쉬우며, 상당히 증가된 depth에서도 정확성을 얻을 수 있다는 comprehensive empirical evidence를 제공한다.

방법
Unreferenced function을 학습하는 대신 layer의 input을 reference하여 residual function을 학습하는 것으로 layer를 재구성한다.

Deep Residual Learning

1. Residual Learning

Motivation

• Counterintuitive phenomena about the degradation problem
• 추가된 레이어를 identity mapping으로 구성할 수 있다면, 더 깊은 모델은 더 얕은 모델보다 training error가 크지 않아야 한다. Degradation problem은 solver가 여러 비선형 레이어로 identity mapping을 근사화하는 데 어려움이 있을 수 있음을 시사한다. Residual learning reformulation을 통해 identity mapping이 최적인 경우 solver는 단순히 identity mapping에 접근하기 위해 여러 비선형 레이어의 가중치를 0으로 유도하면 된다.
• 실제로 identity mapping이 최적이 아니더라도, identity mapping이 reasonable preconditioning을 제공할 수 있다. 실제로 실험을 통해 학습된 residual function이 일반적으로 반응이 작다는 것을 보여주었다.

2. Identity Mapping by Shortcuts

• x와 F의 dimension이 같은 경우
  

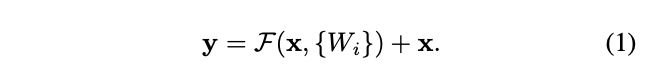
  • Shortcut connections : neither extra parameter nor computation complexity

• x와 F의 dimension이 다른 경우
  

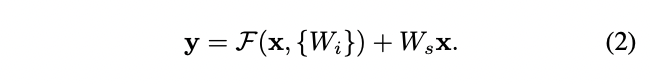
• We can perform a linear projection $W_s$ by the shortcut connections to match the dimensions

• $W_s$ is only used when matching dimensions.

3. Network Architectures

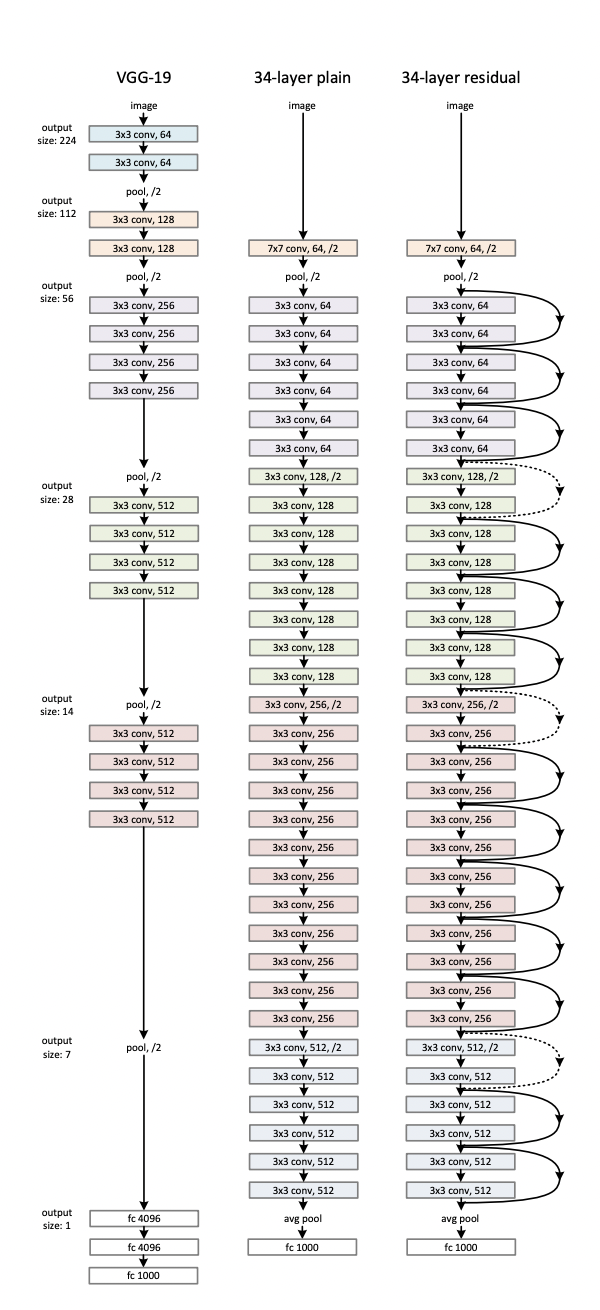
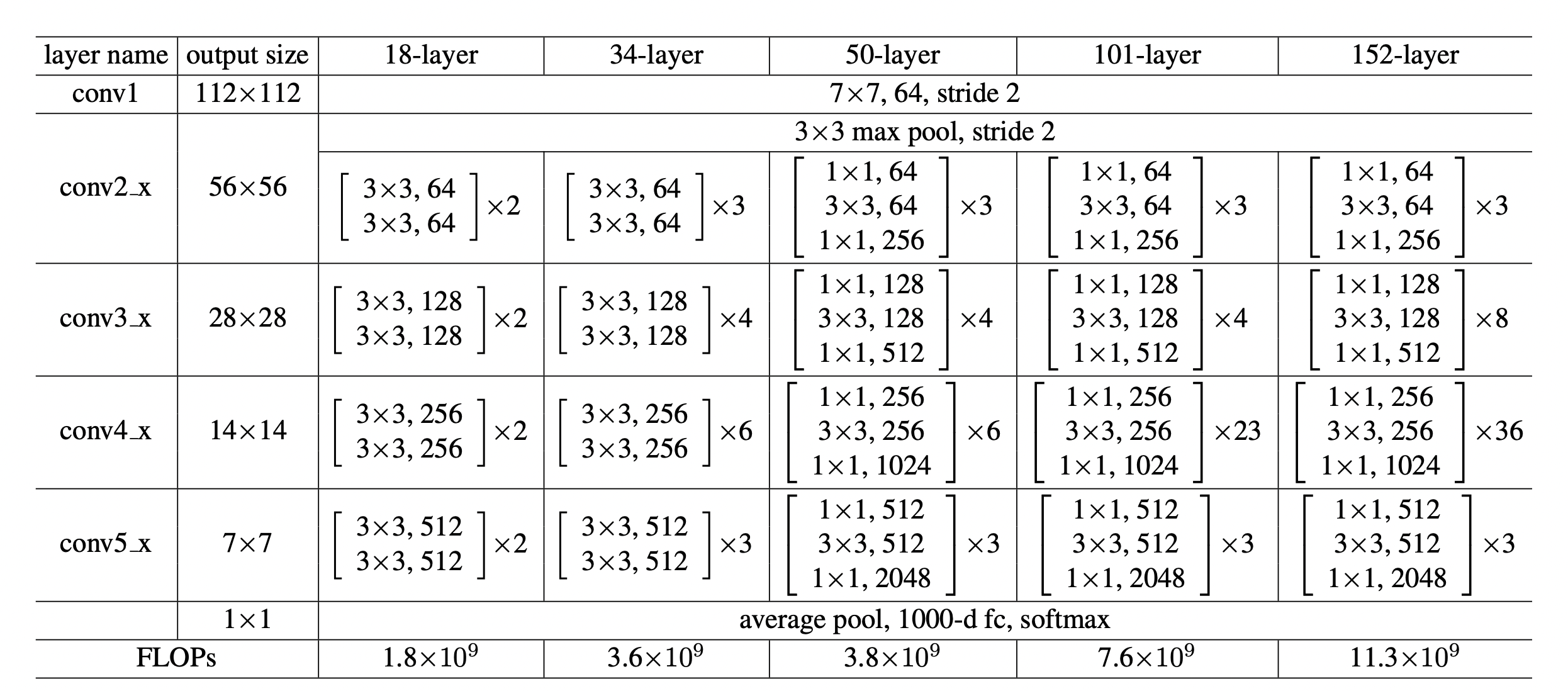
Plain Network

• Inspired by the philosophy of VGG nets
• Convolutional layers mostly have 3x3 filters
• Two simple deisn rules
  • Same output feature map size -> same number of filters
  • If the feature map size is halved, the number of filters is doubled so as to preserve the time complexity per layer.
• Perform downsampling directly by stride 2 convolutional layers
• 네트워크는 global average pooling layer와 1000-way fully-connected layer with softmax로 마무리된다.

Residual Network

• Plain network를 기반으로 하여 shortcut connection을 삽입
• input과 output dimension이 같으면 identity shortcuts(Eqn.(1))가 사용된다.
• Dimension이 증가하면
  • (A) dimension을 증가시키기 위해 zero pad 사용 (no extra parameter)
  • (B) Projection shortcut(Eqn.(2))를 사용하여 dimension match(done by 1x1 convolutions)
  For both options, when the shortcuts go across feature maps of two sizes, they are performed witih a stride of 2.

4. Implementation

• The image is resized with its shorter side randomly sampled in [256, 480] for scale augmentation.
• A 224×224 crop is randomly sampled from an image or its
  horizontal flip, with the per-pixel mean subtracted.
• The standard color augmentation is used.
• Adopt batch normalization (BN) right after each convolution and
  before activation
• Initialize the weights as in [13] and train all plain/residual nets from scratch.
• Use SGD with a mini-batch size of 256
• Learning rate starts from 0.1 and is divided by 10 when the error plateaus
• The models are trained for up to 60 × 104 iterations.
• Use a weight decay of 0.0001 and a momentum of 0.9.
• Do not use dropout.

Test

• For comparison studies we adopt the standard 10-crop testing.

• For best results, we adopt the fully convolutional form as in [41, 13], and average the scores at multiple scales (images are resized such that the shorter side is in {224, 256, 384, 480, 640}).

Experiment

Overview

• ImageNet

  • Our extremely deep residual nets are easy to optimize, but the counterpart “plain” nets (that simply stack layers) exhibit higher training error when the depth increases.
  • Our deep residual nets can easily enjoy accuracy gains from greatly increased depth, producing results substantially better than previous networks.

• CIFAR-10

  • We present successfully trained models on this dataset with
    over 100 layers, and explore models with over 1000 layers.

1. ImageNet Classification

Dataset

• ImageNet 2012 classification dataset
  • Train set : 1.28 million images
  • Validation set : 50k images
  • Test set: 100k images

Plain Networks

18-layer v s 34-layer

• Observations

  • Degradation problem이 나타났다. 훈련 과정 통틀어 34-layer plain net이 더 높은 training error를 가졌으며, 더 높은 validation error를 가졌다.

• 이유 추측

  • BN을 적용했기 때문에 forward 또는 backward signal이 vanish되지는 않았다.
  • 실제로 34-layer plain net은 여전히 경쟁력 있는 정확도를 달성할 수 있으며 solver가 어느 정도 작동함을 시사한다.
  • 이 논문은 deep plain net이 exponentially low conergence rate를 가질 수 있으며, 이는 training error 감소에 영향을 미칠 수 있다고 추측한다.

Residual Networks

18-layer v s 34-layer
Use identity mapping for all shortcuts and zero-padding for increasing dimensions(option A). -> no extra parameter

• Three major observations
  1. 34-layer ResNet is better than the 18-layer ResNet. 34-layer ResNet이 training error가 상당히 더 낮고, validation data에 더 generalizable하다. 이를 통해 ResNet이 degradation problem을 잘 처리하며, 증가된 depth에서 정확도를 얻을 수 있다.
  2. 34-layer Plain net과 비교하여 34-layer ResNet이 training error가 낮고 top-1 error가 낮다. 이 비교는 extremely deep system에 대한 residual learning의 효과를 검증한다.
  3. 18-layer plain과 residual nets는 둘다 상당히 정확하지만, 18-layer ResNet이 더 빠르게 수렴한다. ResNet은 초기 단계에서 더 빠른 convergence을 제공하여 optimization을 용이하게 합니다.

Identity vs. Projection Shortcuts

(A) zero-padding shortcuts are used for increasing dimensions, and all shortcuts are parameterfree
(B) projection shortcuts are used for increasing dimensions, and other
shortcuts are identity
(C) all shortcuts are projections

• Observations
  • A < B < C
  • 하지만 A, B, C간의 차이가 작기 때문에 degradation problem을 다루는 데 projection shortcuts가 중요하지 않다는 것을 알 수 있었고, memory/time complexity와 model size를 줄이기 위해 이 논문에서는 그뒤로 option C는 사용하지 않았다.

Deeper Bottleneck Architectures

다음으로 ImageNet에 대한 보다 심층적인 네트워크에 대해 설명한다. 이 논문은 training time에 대한 우려 때문에, building block을 bottleneck design으로 수정한다.
Time complexity는 전 design과 비슷하다.
Bottleneck design에서는 identity shortcut이 projection에 비해 더 efficient한 model이 된다. Projection을 하면 time complexity와 model size가 double이 되기 때문이다.

• Design

  • 1x1, 3x3, 1x1 convolutions

• 50-layer ResNet

  • 2-layer block을 3-layer bottleneck block으로 대체
  • use option B for increasing dimensions

• 101-layer and 152-layer ResNets

  • 3-layer bottleneck block 사용
  • 152-layer ResNet도 VGG-16/19 net보다 lower complexity를 가진다.

• Observations

  • 50/101/152 layer ResNet이 34-layers보다 상당한 차이로 더 정확하다.
  • Degradation problem이 관찰되지 않았고 상당히 증가된 depth에서 상당한 정확성을 얻을 수 있었다.

CIFAR-10 and Analysis

Analysis of Layer Responses

• Observations
  • ResNets have generally smaller responses than their plain counterparts.
  • We also notice that the deeper ResNet has smaller magnitudes of responses, as evidenced by the comparisons among ResNet-20, 56, and 110 in Fig. 7. When there are more layers, an individual layer of ResNets tends to modify the signal less.

Exploring Over 1000 layers

There are still open problems on such aggressively deep models. The testing result of this 1202-layer network is worse than that of our 110-layer network, although both have similar training error. We argue that this is because of overfitting. The 1202-layer network may be unnecessarily large (19.4M) for this small dataset.