Position Encoding
Position Encoding
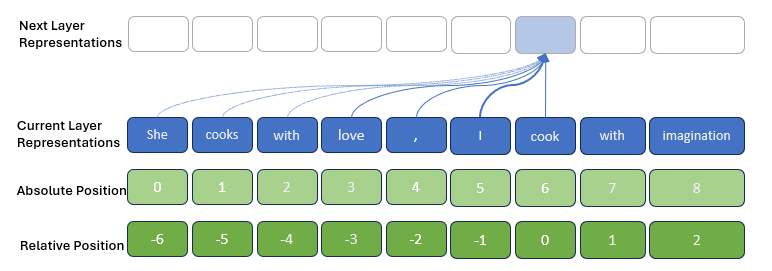
- 모델이 입력 시퀀스의 각 단어가 문장에서 어디에 위치하는지를 알 수 있도록 도와주는 역할
- 트랜스포머 모델은 위치 정보가 없으면 단어 간의 순서를 알 수 없기 때문에, 단어의 순서 정보를 명시적으로 추가해야 함
- 따라서 각 단어의 위치를 나타내는 벡터를 word embedding에 추가함으로써 문맥을 이해하는데 필수적으로 작용!
Absolute Position Encoding (절대 위치 인코딩)
- 각 단어의 절대적 위치를 나타내는 방법
- 각 위치에 대해 고유한 인코딩 벡터를 생성하여, 그 벡터를 word embedding에 추가
- 대표적으로 사인(sin)과 코사인(cos) 함수 기반의 인코딩이 있음
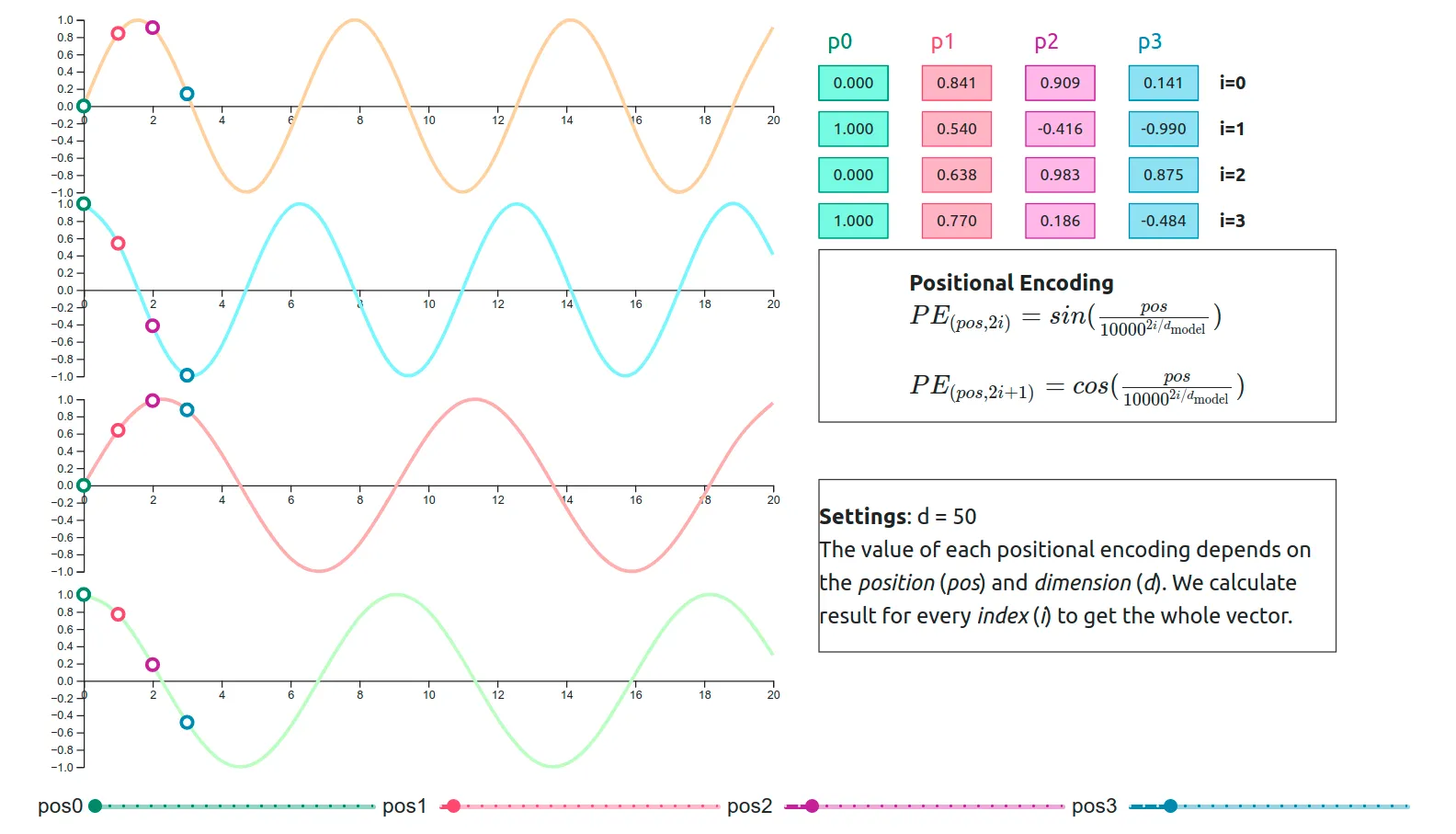
Trainable Position Embedding (학습 가능한 위치 임베딩)
- 위치 정보를 포함한 trainable vector
- BERT에서 주로 사용
Relative Position Encoding (상대 위치 인코딩)
- 단어들 간의 상대적 거리를 고려하여 계산함 (각 단어가 다른 단어들과 얼마나 떨어져 있는지), 계산량이 많아짐!
- self-attention에서 중요한 인코딩: 각 쿼리와 키 간의 관련성을 계산할 때, 단어 간의 상대적 위치 정보를 포함하여 모델이 더 나은 문맥 이해를 할 수 있도록 함
❓그러면 RPE가 추세인건가?
💭현재 트랜스포머 기반 모델이 RPE를 사용해야 한다는 일반적인 규칙은 없습니다. 각 모델의 용도와 상황에 따라 APE와 RPE 중 적절한 방법을 선택해야 합니다. 예를 들어, 긴 문장에서의 문맥 이해가 중요한 경우 RPE가 더 유리할 수 있으며, 고정된 길이의 문장 처리나 절대적인 위치 정보가 중요한 경우 APE가 적합할 수 있습니다.
Abstract
⭐️ 트랜스포머 기반 LM의 학습 과정에 positional information을 통합하는 다양한 방법을 조사
⭐️ 위치 정보를 효과적으로 활용하기 위해 회전 Position Embedding 임베딩(Rotary Position Embedding, RoPE) 이라는 새로운 방법을 제안
⭐️ 제안된 RoPE는 Absolute 위치를 회전 행렬로 인코딩하면서 self-attention 공식에 Relative 위치 의존성을 통합할 수 있음
⭐️ 특히 RoPE는 시퀀스 길이의 유연성, 상대 거리가 증가함에 따른 토큰 간 의존성 감소, 그리고 linear self-attention에 Relative Position encoding을 장착할 수 있는 능력 등의 유용한 특성을 제공
⭐️ RoFormer를 다양한 장문 텍스트 분류 벤치마크 데이터셋에서 평가하여 뛰어난 성능을 증명
Introduction
[자연어 처리에서 위치 인코딩의 중요성]
- 자연어처리에서 단어의 순서는 매우 중요함
- RNNs 기반 모델은 시간에 따라 hidden state를 반복적으로 계산하여 단어 순서를 인코딩
- 반면, CNNs 기반 모델은 보통 위치 무관한 모델로 간주되었지만, 최근 연구는 padding 작업이 위치 정보를 암묵적으로 학습할 수 있음을 보여줌
[Transformer & Self-attention]
- 최근에는 트랜스포머 기반의 PLM이 다양한 자연어 처리 작업에서 SOTA를 달성함
- 이 모델들은 RNN과 CNN 기반 모델과 달리 self-attention을 사용하여 문맥 표현을 보다 잘 포착함
- 이를 통해 병렬화를 진행하였고, RNNs, CNNs보다 더 긴 단어 간 관계를 모델링할 수 있음
[Position encoding 접근 방식]
-
현재 PLMs의 self-attention은 position-agnostic 하다고 알려져 있기 때문에, 이를 보완하기 위해 여러 가지 접근 방식이 제안되었음
-
Absolute encoding: rule-base(sin&cos) 또는 trainble한 encoding vector를 만듬
-
Relative encoding: 주로 Relative position 정보를 self-attention에 사용함
-
하지만 이 접근 방식들은 context representation에 위치 정보를 포함시켜, linear self-attention에서는 적합하지 않을 수 있음
[일반적인 self-attention]
장점: 위치 정보를 포함한 다양한 인코딩 방법을 자유롭게 사용할 수 있습니다. 이는 모델이 문맥과 구조를 더 잘 이해할 수 있도록 돕습니다.
단점: 시퀀스 길이에 따라 메모리 사용량과 계산 비용이 크게 증가합니다. 긴 문장을 처리할 때 효율성이 떨어집니다.
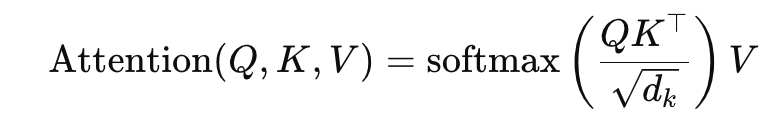
[선형 self-attention]
장점: 메모리 사용량과 계산 비용을 줄여 긴 시퀀스를 효율적으로 처리할 수 있습니다.
단점: Relative 위치 인코딩 같은 복잡한 위치 정보를 다루는 데 제한이 있을 수 있습니다. 이는 모델이 문맥을 완전히 이해하는 데 한계가 될 수 있습니다.
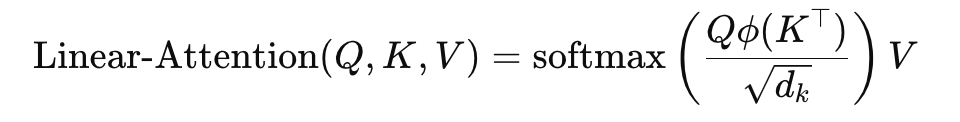
-> ϕ는 dot product 대신 사용되는 특정 함수로, 주로 키 벡터에 대한 변환
-> 계산비용이 O(N^2) -> O(N)으로 줄어들음 -
선형 self-attention은 일반적인 self-attention에서의 쿼리와 키 벡터 간의 모든 점곱 연산을 피하고, 대신 더 효율적인 계산 방식을 사용하기 때문에, 복잡하고 계산이 필요한 Relative 위치 인코딩을 사용하는 것이 더 어려울 수 있음
[Rotary Position Embedding (RoPE)]
- 회전 위치 임베딩(Rotary Position Embedding, RoPE)을 소개
- RoPE는 absolute 위치를 회전 행렬로 인코딩하며, self-attention 공식에 explicit하게 relative 위치 의존성을 통합함
- RoPE의 주요 장점으로는 시퀀스 길이의 유연성, 상대 거리가 증가함에 따라 감소하는 토큰 간 의존성, linear self-attention에 relative 위치 인코딩을 장착할 수 있는 능력이 존재!
- 결국 긴 sequence에 대해 적은 연산량으로, 잘 처리하기 위해서!
상대 거리가 증가함에 따라 감소하는 토큰 간 의존성
상대 거리가 멀어질수록 토큰 간 의존성을 자연스럽게 감소시키는 것은 모델이 중요한 정보에 집중하고, 덜 중요한 관계는 무시할 수 있게 합니다. 이는 계산 효율성을 높이고, 중요한 관계에 대한 학습을 강화합니다.
[Contribution]
- RoPE는 회전 행렬을 통해 문맥 표현에 상대 위치 정보를 명확하게 인코딩
- RoPE의 특성을 연구하여, 상대적 거리 증가에 따라 위치 의존성이 감소하는 자연어 인코딩에 유리한 특성을 보임을 확인함
- 다양한 긴 텍스트 벤치마크 데이터셋에서 RoFormer를 평가한 결과, 일관되게 대안들보다 우수한 성능을 달성!
Proposed approach
⟨fᵩ(xₘ, 𝑚), fₖ(xₙ, 𝑛)⟩ = g(xₘ, xₙ, 𝑚 - 𝑛)
-
단어 임베딩 xₘ, xₙ
-
상대적 위치 m, n
-
오른쪽 항
- 벡터 qₘ와 키 벡터 kₙ의 내적을 계산할 때, 단어 벡터 xₘ, xₙ뿐만 아니라, 이들 간의 상대적 위치 정보 m - n도 포함하도록 하고자 할때, 이는 함수 g를 통해 이루어지며, 이 함수는 두 단어의 벡터와 그들의 상대적 위치를 입력으로 받음
-
왼쪽 항
-
fᵩ(xₘ, 𝑚): 쿼리 벡터 fᵩ는 단어 벡터 xₘ과 그 단어의 위치 m를 인코딩한 결과이며 즉, 이 벡터는 특정 단어와 그 위치 정보를 포함한 표현입니다.
-
fₖ(xₙ, 𝑛): 키 벡터 fₖ는 단어 벡터 xₙ과 그 단어의 위치 n를 인코딩한 결과이며 이는 또 다른 단어와 그 위치 정보를 포함한 표현입니다.
-
내적 (⟨ ⟩): 이 내적 연산은 쿼리 벡터와 키 벡터 간의 유사도를 계산함
-
내적 값이 클수록 두 벡터가 서로 더 유사하다는 것을 의미하며, 이는 두 단어가 문맥적으로 더 관련이 있다는 것을 나타냄!
-
-
따라서, 최종 목표는 상대 위치 정보를 인코딩하기 위해 Relatvie 위치 인코딩을 사용하여(m-n) 함수 fᵩ(xₘ, 𝑚)와 fₖ(xₙ, 𝑛)를 만족시키는 등가의 인코딩 메커니즘 g를 찾는 것!
Rotary position embedding
- 기본 개념: 2차원 예시
- RoPE는 벡터의 위치 정보를 인코딩하기 위해 복소수 형식과 회전 행렬을 사용
- 이를 통해 각 단어 벡터는 해당 위치에 따라 회전됨
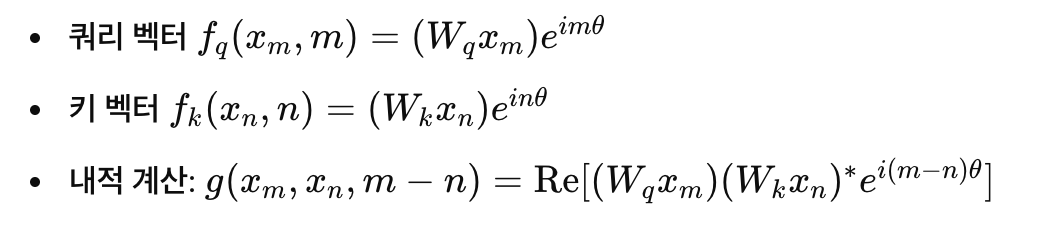
- 여기서, θ는 사전 정의된 상수로 각도 값을 나타내며, Re[⋅]는 복소수의 실수 부분을 의미
- 이 방식은 각 단어 벡터가 위치에 따라 회전하는 것을 의미하며, 즉 RoPE는 단어의 위치를 "회전"이라는 개념으로 표현함
- 예를 들어, 문장에서 첫 번째 단어와 두 번째 단어는 서로 다른 위치에 있기 때문에 벡터가 다른 각도로 회전
- RoPE는 회전 행렬을 사용하여 위치 정보를 인코딩함
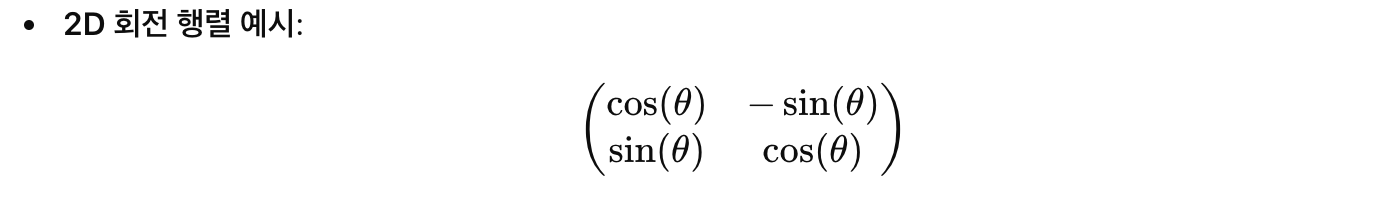
❓왜 갑자기 복소수 회전 변환에서 회전행렬이 나오지?

- 그래서 결국, 아까 말했던 g는 회전행렬이 되는것!
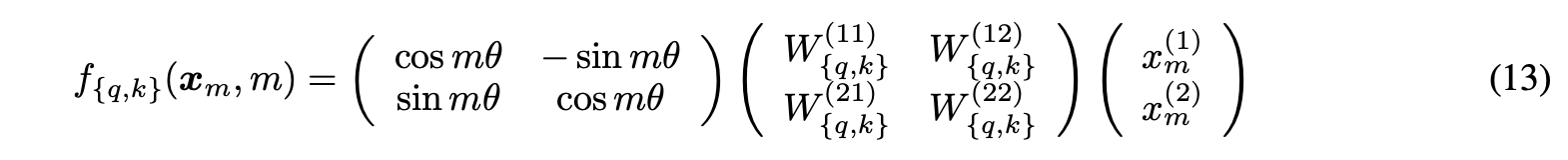
- 그래서 결국, 아까 말했던 g는 회전행렬이 되는것!
- 일반화된 형태
- 2차원 예시에서 확장하여, RoPE는 d차원 공간에서도 사용할 수 있음
- d차원 공간을 d/2개의 부분 공간으로 나누고, 각 부분 공간에서 회전 행렬을 적용

- 여기서, 각 𝜃𝑖 값은 특정 패턴에 따라 설정됨
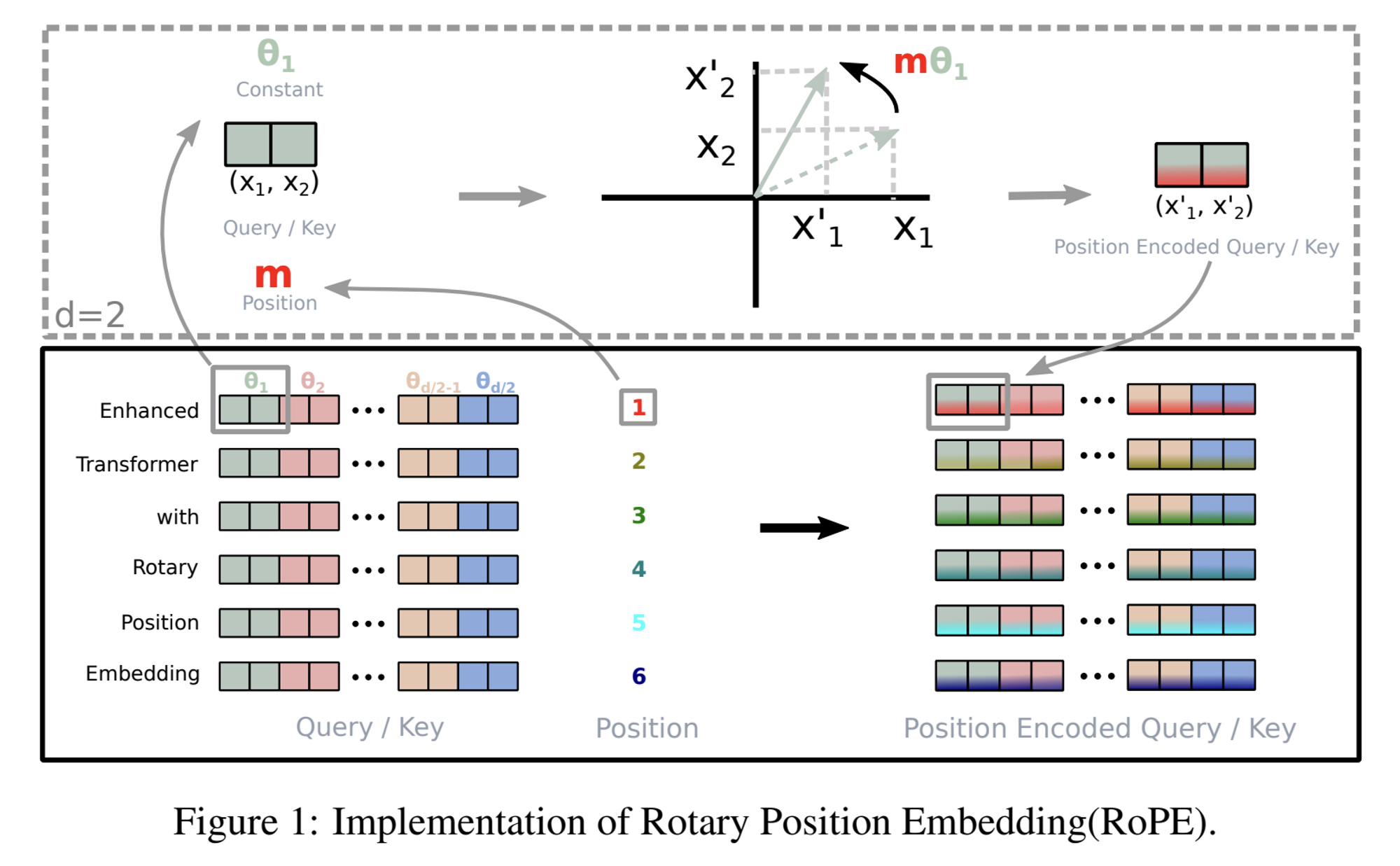
🤗그래서! Absolute 위치를 회전 행렬로 인코딩하면서 self-attention 공식에 Relative 위치 의존성을 통합할 수 있다는 말은?


Properties of RoPE
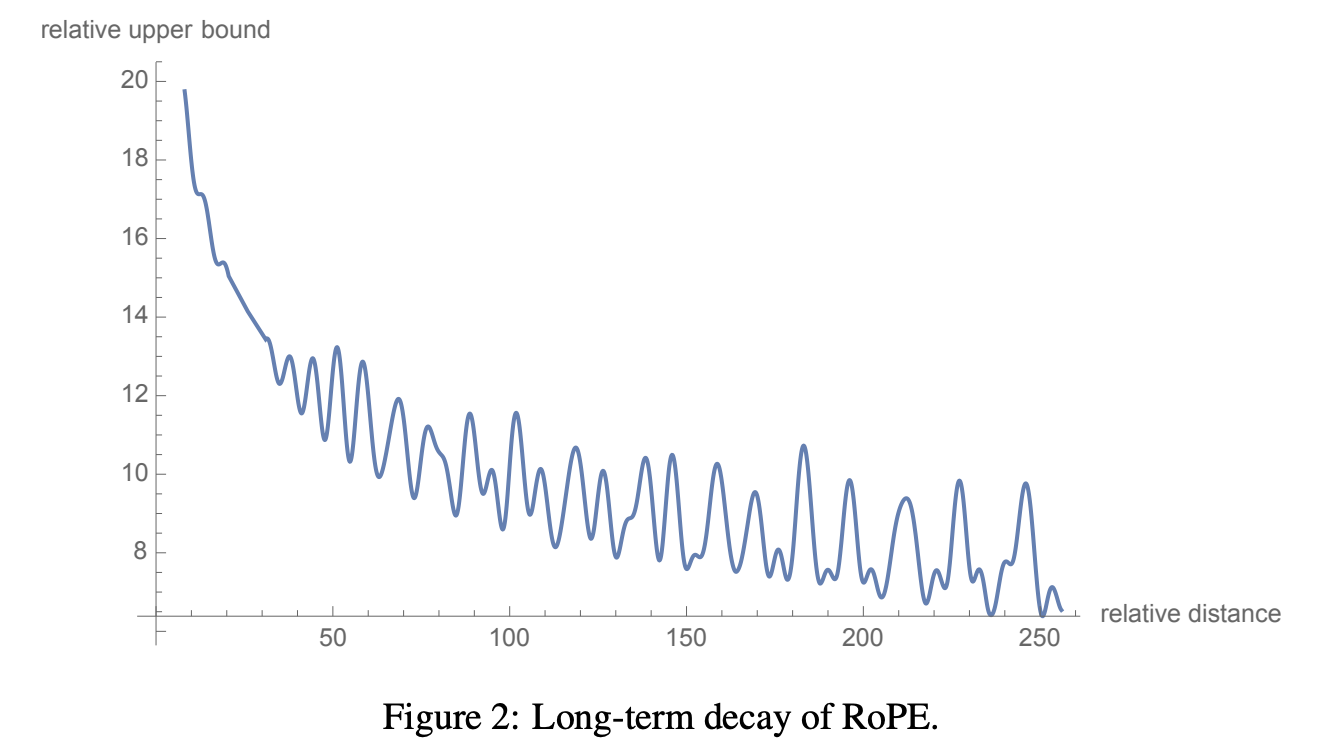
- Long-term Decay
-
RoPE는 긴 거리의 단어 쌍 간의 관계가 약해지는 특성을 가지고 있음 -> Relative position 사용했기때문
-
이는 단어 간의 상대적 거리가 증가할수록 내적(inner-product) 값이 감소하는 것을 의미
-
이러한 특성은 먼 거리에 있는 두 단어가 서로 적은 관련성을 가진다는 직관과 일치!
-
이를 위해 RoPE에서는 각 𝜃𝑖를 10000−2𝑖/𝑑로 설정합니다. 이 설정은 단어 간의 거리가 멀어질수록 연관성이 감소하는 "Long-term Decay" 특성을 제공
-
매우 큰 값을 갖는 것을 막고, 회전 각도를 적절한 수준으로 조정하는 역할을 함

-
- RoPE with linear attention
-
self-attention
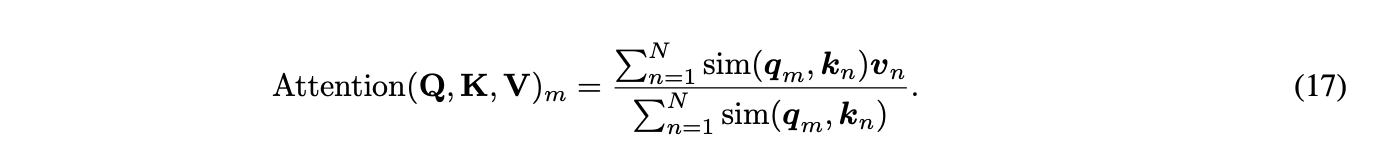
-
linear self-attention
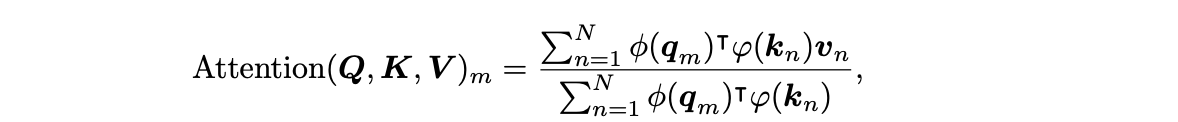
-
쿼리와 키 벡터를 변환하는 비음수 함수 사용하여 계산 비용을 줄임
-
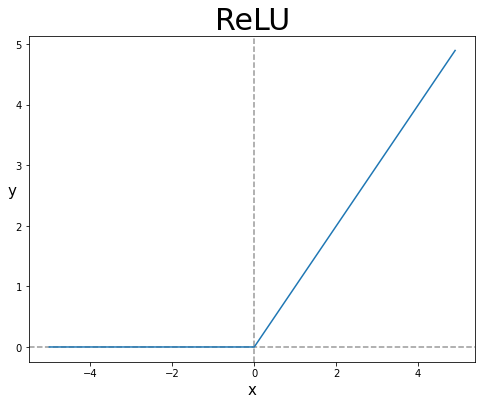
elu(x)+1이나 relu(𝑥)와 같은 함수
-
많은 요소들이 0 또는 작은 값이 되어, 실제로 계산해야 하는 연산의 수를 줄임
-
-
linear self attention with RoPE

Experiments and Evaluation
1. Machine Translation
- WMT 2014 영어-독일어 데이터셋을 사용하여 평가
- self-attention layer에 RoPE 추가
- BLEU

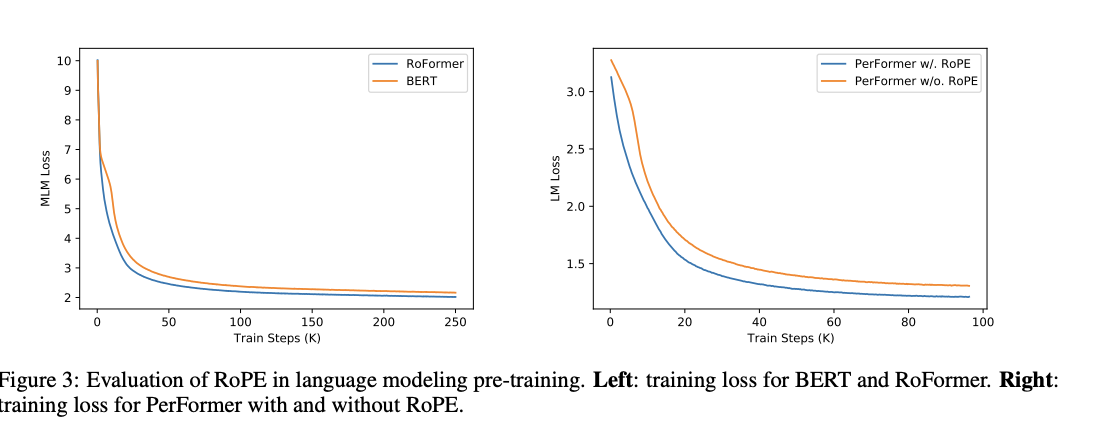
2. Pre-training Language Modeling
- RoFormer의 문맥적 표현 학습 성능을 검증하기 위해, BERT의 기존 sin 위치 인코딩을 RoPE로 대체
- Huggingface Datasets에서 제공하는 BookCorpus와 Wikipedia Corpus를 사용
- MLM Loss 사용
- Vanilla BERT와 비교했을 때, RoFormer는 더 빠르게 수렴하는 경향
3. Fine-tuning on GLUE tasks
- RoFormer의 pre-trained weight를 다양한 GLUE task에서 fine-tuning하여, 다운스트림 NLP 작업에서의 일반화 능력을 평가
- 평가에 사용된 GLUE 데이터셋은 MRPC, SST-2, QNLI, STS-B, QQP, MNLI
- 평가 지표로는 MRPC와 QQP에서는 F1 점수, STS-B에서는 스피어만 상관계수, 나머지 작업에서는 정확도를 사용
- RoFormer는 6개의 데이터셋 중 3개에서 BERT를 능가했으며, 특히 몇몇 데이터셋에서는 상당한 개선을 보임

4. Performer with RoPE
- PerFormer는 입력 시퀀스 길이에 따라 계산 비용이 증가하는 문제를 해결하기 위해 설계된 linear self-attention을 도입한 모델
- RoPE는 상대적 위치 인코딩을 PerFormer에 쉽게 통합할 수 있어 선형적으로 증가하는 복잡도를 유지하면서도 위치 정보를 효과적으로 처리할 수 있음
- Enwik8 데이터셋을 사용하여 언어 모델링 사전 학습 작업을 수행
- RoPE를 PerFormer에 적용하면 동일한 학습 스텝에서 더 빠르게 수렴하고 손실이 낮아지는 결과를 보임
5. Evaluation on Chinese Data
- RoFormer의 성능을 장문 텍스트에서 검증하기 위해, 512자 이상의 긴 문서에 대한 실험을 진행
- 기존 WoBERT 모델에서 절대 위치 인코딩을 RoPE로 대체하여 실험을 수행
- 중국어에서 BERT, WoBERT, NEZHA 등과 같은 사전 학습된 트랜스포머 기반 모델과의 비교를 위해, 토큰화 수준과 위치 인코딩 방식을 정리

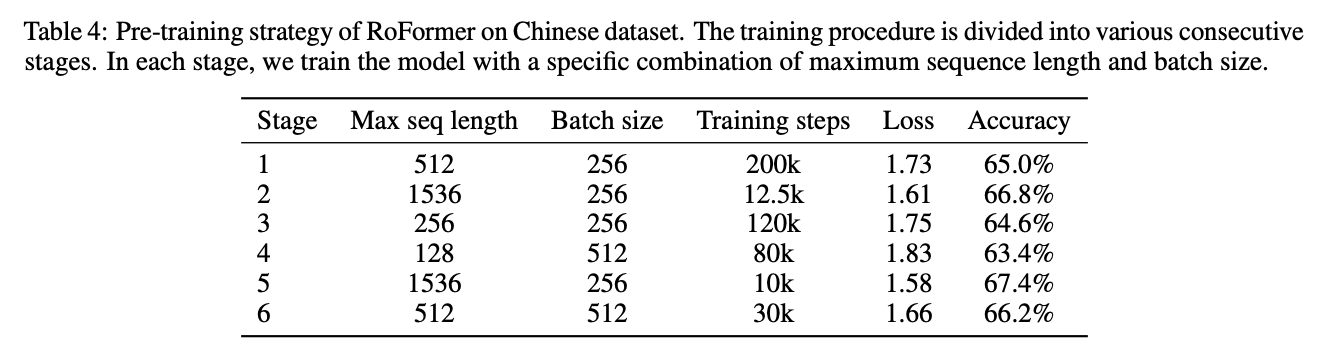
- 약 34GB의 중국어 위키백과, 뉴스, 포럼 데이터에서 RoFormer를 pre-training
- 다양한 시나리오에 맞추기 위해 배치 크기와 최대 입력 시퀀스 길이를 변경하면서 여러 단계로 학습을 진행
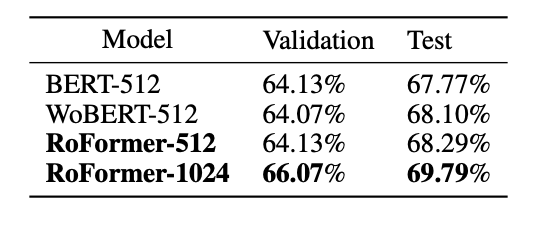
- Downstream task
- RoFormer의 긴 텍스트 처리 능력을 입증하기 위해 CAIL2019-SCM(Chinese AI and Law 2019 Similar Case Matching) 데이터셋을 사용
- 이 데이터셋은 중국 대법원에서 발행한 8964개의 사건 사례를 포함하며, (A, B) 쌍이 (A, C) 쌍보다 더 유사한지를 예측하는 작업을 수행하는데, 기존 방법들은 문서 길이(대부분 512자 이상) 때문에 이 데이터셋에서 성과를 내지 못함
- 최대 입력 텍스트 길이를 1024자로 늘렸을 때, RoFormer는 WoBERT를 절대적으로 1.5% 더 높은 성능을 보임 (긴 언어 이해능력)
Code,,
def rotate_half(x):
x = rearrange(x, '... (d r) -> ... d r', r=2)
x1, x2 = x.unbind(dim=-1)
x = torch.stack((-x2, x1), dim=-1)
return rearrange(x, '... d r -> ... (d r)')
def apply_rotary_emb(freqs: torch.Tensor, t: torch.Tensor, start_index=0):
rot_dim = freqs.shape[-1]
end_index = start_index + rot_dim
assert rot_dim <= t.shape[-1], f'feature dimension {t.shape[-1]} is not of sufficient size to rotate in all the positions {rot_dim}'
t_left, t_right = t[..., :start_index], t[..., start_index:end_index]
t = torch.cat((t_left, t_right * freqs.cos() + rotate_half(t_right) * freqs.sin(), t[..., end_index:]), dim=-1)
return t
- rot_dim = freqs.shape[-1]: 회전 차원을 가져옵니다.
- end_index = start_index + rot_dim: 회전 차원의 끝 인덱스를 계산합니다.
- assert rot_dim <= t.shape[-1], ...: 입력 텐서 t의 차원이 충분한지 확인합니다.
- t_left, t_right = t[..., :start_index], t[..., start_index:end_index]: 입력 텐서를 회전 차원 기준으로 나눕니다.
- t = torch.cat((t_left, t_right freqs.cos() + rotate_half(t_right) freqs.sin(), t[..., end_index:]), dim=-1): 회전 변환을 적용하고 결합합니다.
rot_q = apply_rotary_emb(freqs, q)
rot_k = apply_rotary_emb(freqs, q)
Summary
- RoPE는 절대 위치와 상대 위치 정보를 벡터에 인코딩하기 위해 회전 행렬을 사용
- 이는 단어 벡터를 복소수 평면에서 회전시키는 방식으로, 위치에 따른 차이를 자연스럽게 표현할 수 있음
- 상대 위치 의존성: RoPE는 쿼리와 키 벡터 간의 상대적 위치 정보를 반영하여, 멀리 떨어진 단어 쌍 간의 내적 값을 줄여주는 long-term decay특성을 제공
- linear self-attention의 통합: RoPE는 선형 linear self-attention과 쉽게 결합될 수 있으며, 계산 비용을 줄이면서도 위치 정보를 효과적으로 처리할 수 있음
🫨감사합니닷

relative position embedding을 각도로 접근한다는 방법이 신선한것 같습니다!