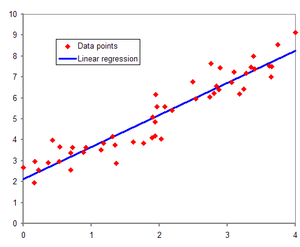
선형회귀모델이란?
선형회귀 모델은 지도 학습 알고리즘으로 수치 예측을 할때 주로 사용되는 기본적인 모델이면서 매우 강력하다. 데이터셋은 크게 두가지 종류의 변수로 나눌 수 있다. 독립변수와 종속변수이다. 독립 변수라 함은 어떤 영향도 받지 않는 말그대로 독립적인 변수이다. 다른 말로는 인풋 변수, 예측 변수라고도 할 수 있다. 이러한 독립 변수들에 영향을 받고 실제로 값이 변할 수 있는 변수는 종속 변수라고 하는 것이다. 쉽게 말해 우리가 구하고자 하는 아웃풋이 바로 이 종속 변수인 것이다. 선형 회귀는 이러한 독립 변수와 종속 변수의 관계를 선형식을 이용하여 설명하는 모델이다.
선형 회귀의 가정
선형 회귀 분석을 수행하기 위해서는 다양한 가정이 기반이 된다. 하지만 항상 가정을 만족해야하는 것은 아니고 필요에 따라서 버릴 가정은 버리는 경우도 종종 있다. 우선 기본적으로 4가지의 기본 가정을 만족해야한다. 다시 한번 말하지만 이 가정이 절대적인 것은 아니고 좋은 모델을 만들기 위한 가정이다.
- 선형성: 위에서 언급했듯 선형성이라는 것은 독립변수와 종속변수가 선형적인 관계를 가져야만 한다는 것이다.
- 독립성: 다중회귀모형에 투입되는 여러 변수들간에는 특정한 관계가 없어야 한다는 것이다.
- 등분산성: 등분산성은 분산이 같다는 의미로 통계학에서는 모든 확률 변수가 같은 유한 분산을 가지는 성질을 가정한다.
- 정규성: 이 또한 잔차와 연관이 되어있는데, 정규분포에서는 잔차의 형태를 최대한 간단하게 두기 위해서 가정하고 모형을 만든다고 한다.
선형 회귀 모델의 손실 함수
선형 회귀에는 평균 제곱 오차(MSE)가 등장한다. MSE라고 하면 쉽게 말해 실제 데이터와 예측으로 나온 데이터가 평균적으로 얼마나 떨어져 있는지를 의미한다. 제곱을 하는 이유는 더 차이를 더 부각하고 양수로 바꾸기 위함이다. MSE를 언급하는 이유는 선형회귀에서 MSE가 손실함수로 나오는 아웃풋이기 때문이다. 어쨌든 최종적으로 원하는 결과는 손실 함수를 최소화 시키는 것이라고 볼 수 있다. 여기서 우리가 도출해낼 수 있는 점 중 하나는 제곱을 곱했기 때문에 이식이 이차식이 될것이라는 것이다. 아래의 사진을 보면 조금더 편하게 이해를 할 수 있을 것 같다.
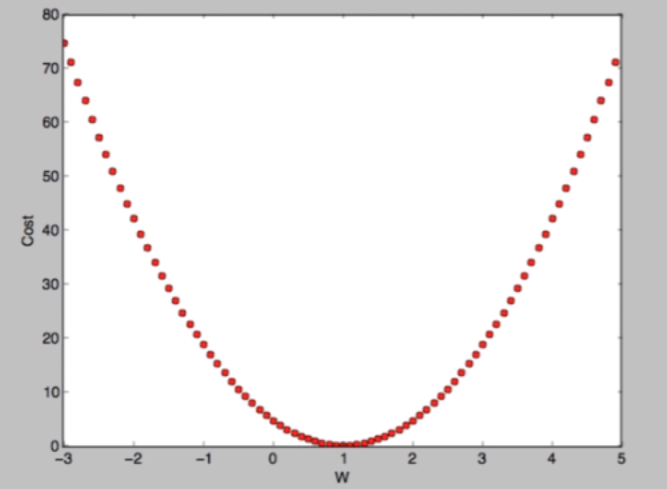
이러한 상황에서 우리는 결국 극점/최소점을 찾고자 하는데 어떻게 찾을 수 있을까? 이 때 경사하강법이라는 것이 등장하게 된다.
경사하강법
경사하강법은 미분과 밀접한 관계가 있다. 결국에 이차식에서 어느 지점에서 미분을 하게 되면 결국 그 지점에서의 기울기를 보여주게 되는데 최솟점이 되는 지점은 기울기가 평평하므로 0이 되게 된다. 점차 점차 기울기가 0으로 가까워 지는 방향으로 이동을 하며 0이 되는 지점을 찾게 되는데, 이 과정을 대부분 산을 내려가는 것과 유사하다고 한다. 당연히 이 내려가는 속도를 우리가 조정해줄 수 있지만, 산을 너무 천천히 내려가면 자세한 값들을 찾을 수는 있겠지만 속도가 매우 느려질 것이다. 반대로 내려가는 보폭을 너무 크게 한다면 최소점이 되는 지점을 놓치고 지나갈 수 있지만, 시간이 빠르다는 장점을 가지고 있다. 하지만 경사 하강법을 여러가지 문제 직면할 수 있는 다차수에 대한 그래프의 경우 글로벌 미니멈을 찾는 것이 아닌 시작하는 지점에 따라서 로컬 미니멈을 찾거나 혹은 saddle point 라는 최소도 최대도 아니지만 기울기가 0인 지점을 찾을 수도 있다.
장단점
장점
- 설명 변수 변화에 따른 반응 변수의 변화가 해석 가능하다.
- 비교적 구현이 간단하다.
- 가정이 맞으면 최적의 값을 얻을 수 있다.
- 학습 속도가 빠르고 예측도 빠르다.
단점
- 선형 함수라는 제약이 있으므로 예측력이 좋지는 않을 수 있다.
- 다중공산성이 존재하면 신뢰성이 떨어진다.
- 이상치에 민감하다.
- 계수들의 값들이 왜 그러한지 명확하지 않을 수 있다.
파이썬으로 구현하기
아래의 코드를 이용하여 모델을 불러와 변수에 저장한다.
from sklearn import linear_model
model_lr = linear_model.LinearRegression()분석할 X_train과 y_train을 선형회귀모델로 학습 시키기 위해 다음과 같은 코드를 실행한다.
model_lr.fit(X_train, y_train)R2score과 같이 정확도를 확인하고자 한다면 다음과 같은 코드를 실행시키면 된다.
model_lr.score(X_train, y_train) #훈련 데이터의 경우
model_lr.score(X_valid, y_valid) #검증 데이터의 경우