Feature Engineering

사진 출처

왜 Feature Engineering을 하는 것인가?

데이터의 종류는 정말 다양한만큼 EDA를 통해 데이터를 파악하는 작업이 매우 중요하다. 또한 EDA를 하면 Feature을 select해야 하는 경우도 자주 생기는데, 그것만을 이용해서 머신러닝을 돌리거나 분석을 하기에는 부족한 경우가 종종 생기곤 한다. 이러한 경우에 Feature Engineering이 필요하다.

Feature Engineering의 대표적인 기법으로,

• 결측치 채우기
• 이상치 처리하기
• 변수 스케일링과 트랜스포메이션하기
• 로그 변환하기
• Binning 하기
• 인코딩하기
• 파생변수 생성하기

등등이 있다.

결측치 채우기

데이터 속에 결측치가 있는 경우 이를 해결하기 위한 가장 간단한 방법으로는 .dropna()와 같음 함수를 이용하여 null이 있는 행을 전부 드랍해버리는 방법일 것이다. 하지만 이런 경우 데이터의 갯수가 너무 적어지거나 그외의 다른 변수의 값이 중요한 행이라면 결과에 큰 영향을 미칠 수 있다.

결측치를 채우는 방법 또한 정말 많은 방법이 있을 것이다.

1. 랜덤하게 채우기
2. 특정값으로 결측치를 채우기 (ex: 0)
3. 결측값을 앞 방향 혹은 뒤방향으로 채우기
4. 변수별 평균, 중간값, 최빈값 등등으로 채우기

외에도 정말 많은 방법들이 있다.

df.fillna(method='ffill') #앞방향
df.fillna(method='bfill') #뒷방향

위와 같이 fillna라는 함수를 이용하여 결측값을 쉽게 대체할 수 있다.

이상치 처리하기

이상치라 함은 데이터셋 속에서 범위를 벗어나는 극단적인 값을 의미한다. 이러한 이상치는 평균, 총합, 분산 들 여러 지표들에 영향을 미쳐 문제를 일으키기도 한다. 그러므로 상황에 따라 upperlimit 혹은 underlimit을 정해주어 이상치를 제거하거나, 대체하는 방법을 통해 영향을 감소 시킨다. 대부분 이상치를 확인하기 위한 좋은 시각적 방법으로 박스 플롯을 이용한다.

그러나 무조건 적으로 이상치는 제거하거나 처리해주어야 하는 대상이 아닐 수도 있다는 점을 유의하여야 한다.

변수 스케일링과 트랜스포메이션하기

Feature scaling 이라 함은 서로 다른 범위를 가지는 변수들을 일정한 수준으로 맞추는 것이다. 왜 이 작업이 필요할까?

예를 들어 금액과 관련된 변수와 수량에 관련된 변수가 있다고 가정하자. 금액과 관련된 변수의 범위는 20,000 ~ 500,000 인 반면 수량은 10 ~ 20이라고 하였을 때, 서로 다른 단위에 따른 영향을 미치면 안 될 것이다. 따라서 범위나 단위가 달라 발생하는 문제를 스케일링을 통해 예방 가능하다.

또한 머신러닝 모델이 특정 데이터에게 편향성을 가지게 되는 것을 방지하거나, 모델이 학습하는데 있어서 bias가 달라지는 것을 막기 위해 범위를 맞춰주는 것은 매우 필요하다.

스케일링 방법에는

1. Standard Scaler
2. MinMaxScaler
3. RobustScaler

그 외에도 Normalizer, MaxAbsScaler 등 여러 종류의 기법들이 있다.

Standard Scaler

한국어로는 표준화란 평균이 0이고 분산이 1인 가우시안 정규분포를 가지도록 변환하는 것을 의미한다. 이는 linear regression, logistic regression, SupportVectorMachine 과 같은 모델들에서 특히 자주 쓰이는데, 이 모델들이 가우시안 분포를 가진다는 가정하에 구현되기 때문이다.

이때 이상치가 있는 변수라면 평균과 분산에 영향을 주기 때문에 가급적 처리해주고 진행하는 것이 좋다.
sklearn을 이용하여 이를 진행하고자 한다면 코드는 다음과 같다.

from sklearn.preprocessing import StandardScaler
ss = StandardScaler()

#방법 1
ss.fit(X_train)
X_train_scaled = ss.transform(X_train)

#방법 2
X_train_scaled = ss.fit_transform(X_train)

sklearn을 사용하는 방식에 대부분 비슷하다는 것을 눈치 챌 수 있다. fit을 시킨후 원하고자 하는 스케일링 방법으로 transform 시켜준다. 위의 두 방법중 어느것을 사용하여도 결과는 같다. 여기서 주의할 점은 fit은 train 데이터 셋을 통해 해주어야 하고 test는 transform만을 이용하여 적용시켜 주어야 한다는 것이다. 물론 전체 데이터셋뿐 아니라 특정 변수에 대한 스케일링도 가능하므로 여러 방법으로 활용을 할 수 있다.

MinMax Scaler

MinMax 스케일링은 이름이 정말 직관적인거 같다. 이 스케일링의 컨셉은 모든 값들이 0과 1사이의 값으로 이루어지게끔 구성하는 것이다. 그렇다면 0과 1은 누구인가? 를 생각해보면 데이터 혹은 변수 내에서 가장 큰 값이 1 가장 작은 값이 0이 되어 이를 기준으로 나머지 데이터들을 바꾼다고 생각하면 편할 것 같다. 여기서 눈치 챌 수 있는 점은 이상치에 민감하다는 것이다. 만약 이상치가 존재하면 최대값과 최솟값이 기준이 되는 이 스케일링 기법에서 당연히 제대로 될리가 없으므로 이점을 유의하여야 할 것이다.

sklearn을 이용하여 이를 진행하고자 한다면 코드는 다음과 같다.

from sklearn.preprocessing import MinMaxScaler

mms = MinMaxScaler()

#방법 1
mms.fit(X_train)
X_train_scaled = mms.transform(X_train)

#방법 2
X_train_scaled = mms.fit_transform(X_train)

Robust Scaler

도대체 왜 스케일링 기법들은 이상치에 이리도 민감한 것인가? 라고 생각하였다면 Robust Scaler를 살펴보면 될 것 같다. Robust라는 이름에서부터 알 수 있듯이 뭔가 덜 민감할 것 같다. Robust scler은 IQR(사분위수)을 기준으로 스케일링 한다. 그러므로 standard scaler보다 더 큰 최솟값과 더 작은 최댓값을 가져 이상치의 영향을 덜 받게 된다. 그렇기 때문에 스케일링을 하고 나면 표준화를 하였을 때부터 데이터가 더 넓게 분포한다는 특징이 있다.

sklearn을 이용하여 이를 진행하고자 한다면 코드는 다음과 같다.

from sklearn.preprocessing import RobustScaler

rbs = RobustScaler()

#방법 1
rbs.fit(X_train)
X_train_scaled = rbs.transform(X_train)

#방법 2
X_train_scaled = rbs.fit_transform(X_train)

계속해서 transform 이라는 녀석이 등장하는데, 데이터가 단순히 변환을 거친 후에 원래 데이터와 같은 사이즈의 형태를 취하도록 해주는 함수이다.

로그 변환하기

데이터 분석을 하면 log 변환을 하는 경우를 심심찮게 볼 수 있는데, 그 전에 왜도와 첨도에 대해 알아보자.

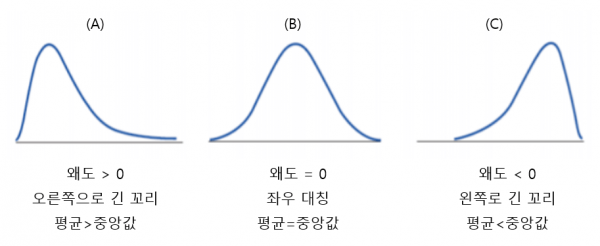
Skewness(왜도)

사진 출처

왜도의 다른 말은 비대칭도이다. 무엇의 비대칭도 일까? 바로 정규분포에 비해 얼마나 비대칭이냐를 의미한다. 쉽게 말해,

• 왜도 < 0 이면 확률 밀도함수의 왼쪽 꼬리가 길다. 즉, 중앙값을 포함한 데이터가 정규분포에 비해 오른쪽에 더 많이 분포 되어있다.
• 왜도 > 0 이면 확률 밀도함수의 오른쪽 꼬리가 길다. 즉, 중앙값을 포함한 데이터가 정규분포에 비해 왼쪽에 더 많이 분포 되어있다.

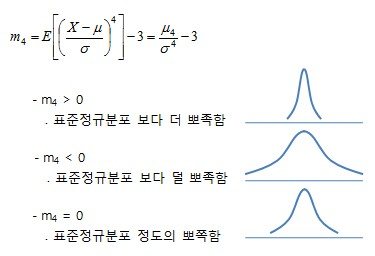
Kurtosis(첨도)

사진 출처

첨도는 얼마나 확률분포가 얼마나 뾰족하냐이다. 즉, 데이터가 중심에 몰려있는 정도를 의미하고, 대부분

• k가 3에 가까울 수록 산포도는 정규 분포에 가깝고
• k<3면 정규분포 보다 덜 뾰족하고
• k>3이면 정규분포보다 뾰족하다고

해석한다.

그래서 로그변환을 왜 사용하는가?

로그 변환에 대해 알아보자면서 계속 정규분포와 관련된 얘기를 하였는데 그 이유는 로그 변환을 하는 이유가 정규성을 높이기 위함이기 때문이다. log 변환은 데이터 간의 편차를 줄여준다. 편차가 줄어듦으로써 왜도와 첨도가 줄어들게 되고 이는 곳 정규성을 높연준다는 뜻이다. 즉, 큰수는 작게 만들어주고, 복잡한 계산은 간편하게 만들어준다.

사용의 예를 코드로 들어보자면,

train['target_log1p'] = np.log1p(train["target"])
# np.log1p(train["target"]) == np.log(train['target'] + 1)

와 같이 어떤 타겟 변수 값을 로그 변환하여 사용해볼 수 있을 것이다. 근데 왜 1p(1을 더해준다)를 하여 로그를 취해줄까? 이는 음의 무한대 값이 나오는 것을 방지하기 위해서이다. 활용 방법으로는 위에서 scaling을 통해 scaling을 하고 난 후에 로그 변환을 해주는 방법도 있을 것이다.

반대로 위의 값을 다시 원래대로 돌리고 싶으면 어떻게 해야할까?

train['target] = np.expm1(train['target_log1p'])
# np.exp(train["target_log1p"])-1 == np.expm1(train["target_log1p"])

지수를 취하면 될 것이다.

Binning 하기

한국어로는 구간화라고 할 수 있는데, 우선 코드 부터 알아보자.

pd.cut('변수명')
pd.qcut('변수명')

우선 cut은 변수를 일정하게 분할하여 준다. qcut의 경우 데이터의 분포를 비슷한 크기의 크룹으로 분할한다.

cut

cut은 쉽게 말해서 절대평가라고 생각하자. 어느 학교에서 아이들의 성적을 절대평가로 매긴다고 하였을 때, 0~20, 20~40, 40~60, 60~80, 80~100으로 구간을 나누어 분할하게 될 것이다. 당연히 각 구간마다 학생 수는 매우 다를수도 아닐 수도 있을 것이다.

qcut

qcut은 상대평가이다. 상대평가는 점수를 기준으로 구간을 나누는 것이 아닌 학생 점수의 비율로 나뉘어진다. 즉, 상위 20%, 20%~40%, ~~ 각 구간에 분포하는 학생수는 비교적 균등할 것이다. 하지만 각 점수 범위는 균등하지 못할 것이다.

구간화는 나이와 같은 수치형 변수를 구간으로 나눔으로써 더 높은 효율을 낼 수 있을 때 사용하는 것이 바람직할 것이다.

인코딩 및 파생변수 생성하기

머신러닝을 돌리고자 할 때 범주형 데이터에 문자가 들어가 돌아가지 않는 경우가 종종 있다. 이러한 경우 사용할 수 있는 것이 인코딩이다. 인코딩 종류는 정말 다양한데 두가지만 알아보자.

One Hot Encoding

이름에서도 알 수 있듯이 0과 1로만 구성된 벡터로 표현하는 기법이다. 예를 들어 도시라는 변수가 '서울', '부산', '강원도' 로 구성되어 있을때 원핫 인코딩을 사용하면 다음과 같이 된다.

도시	도시_서울	도시_부산	도시_강원도
서울	1	0	0
부산	0	1	0
강원도	0	0	1

코드로 이렇게 만들고자 한다면, 다음과 같다.

# 방법1
df = pd.get_dummies(df[['도시']])

# 방법2
from sklearn.preprocessing import OneHotEncoder

ohe = OneHotEncoder(sparse=False)
ohe.fit(df[['도시']])
ohe_encoded=ohe.transform(df[['도시']])
df[ohe.categories_[0]]=ohe_encoded

sparse는 matrix를 반환한다는 것인데 우리는 array가 필요하므로 False를 넣어주고 이를 각 카테고리 이름에 맞는 변수에 넣어준다.

범주가 많지 않을때 사용하면 매우 유용할 것 같다. 또한 순서성이 없는 경우에도 유용하게 사용할 수 있을 것이다.

Label Encoding

Label encoding이란 예를 들어 온도에 대한 변수가 cold, warm, hot으로 이루어져 있다고 할때 각각의 값을 1,2,3으로 바꾸는 것이다. 코드를 먼저 보자면 다음과 같다.

from sklearn.preprocessing import LabelEncoder
df["Temperature_encoder"] = LabelEncoder().fit_transform(df[Temperature])

유용하게 쓰일 수 있을 것 같다.

파생변수 만들기

파생 변수를 만드는 것에 있어서는 어떤 규칙이 있는 것은 아니고, 예를 들어 설명하자면 경도와 위도에 대한 두개의 변수가 있는 경우 이 두개의 변수를 각각 사용하기 보다는 어떤 특정 지점에서의 거리를 계산하는 것이 더 합리적이라고 판단하였다고 가정해보자. 이런 경우 어떤 특정 지점으로 부터의 유크리디언 거리를 구한 값들로 구성된 변수를 하나 만들텐데 이를 파생변수라고 한다. 파생변수를 잘 활용하면 데이터를 줄이는 것 뿐 아니라 더 유의미한 정보를 많이 이끌어낼 수 있다.

결론

결론 적으로 머신러닝을 다루다 보면 파라미터들을 다루면서 성능을 개선 시키는 경우도 많지만 특성들을 가공해가며 모델의 성능을 개선하는 경우도 정말 많다. 그러므로 많은 데이터를 만져보며 특성을 다루는 경험을 쌓는 것이 매우 도움이 될 것이다.