[이미지처리바이블] 2장 이미지 처리 기초

Changh2·2025년 3월 22일

Computer Vision Image Processing 이미지처리 컴퓨터비전

이미지처리바이블

목록 보기

2/7

[이미지 처리 바이블] 교재 2장을 기반으로 작성되었습니다.

2.1 이미지란?

2.1.1 디지털 이미지의 구조

픽셀

> 모든 디지털 이미지의 핵심, 화면을 구성하는 가장 작은 요소

해상도: 이미지가 보유하고 있는 픽셀의 양

픽셀 밀도: 디스플레이의 픽셀이 얼마나 촘촘하게 배열되어 있는지를 나타내는 척도

무손실 압축과 손실 압축

무손실 압축: PNG (Portable Network Graphics)

손실 압축: JPEG (Joint Photographic Experts Group)

>> 이미지 편집 후 JPEG로 저장할 때마다 손실 압축이 다시 적용되므로 품질이 저하됨
>> 전처리 및 모델리 과정에선 무손실 형식인 PNG로 작업 후 최종 결과물 배포를 위해 JPEG로 저장함

2.1.2 색 공간 이해하기

색 공간

그레이 스케일

픽셀에 다양한 색상 스펙트럼 없이 '밝기'를 나타내는 값만 주어지며,
0은 빛이 없는 상태(검은색)를 나타내고, 255는 최대 밝기(흰색)를 나타냄
>> 단순하기에 저장 용량이 작고, 처리 속도가 높음
>> 에지 감지나 텍스처 분석과 같은 특정 이미지 처리 작업엔 색상이 방해되므로 적합함

RGB

Red, Green, Blue 세 가지 색상은 각각의 채널이라는 이름으로 표현됨
ex) Red 채널의 빛을 최대 강도로 발하고, Green, Blue 채널에선 빛을 발하지 않는 픽셀
>> 빨간색 픽셀

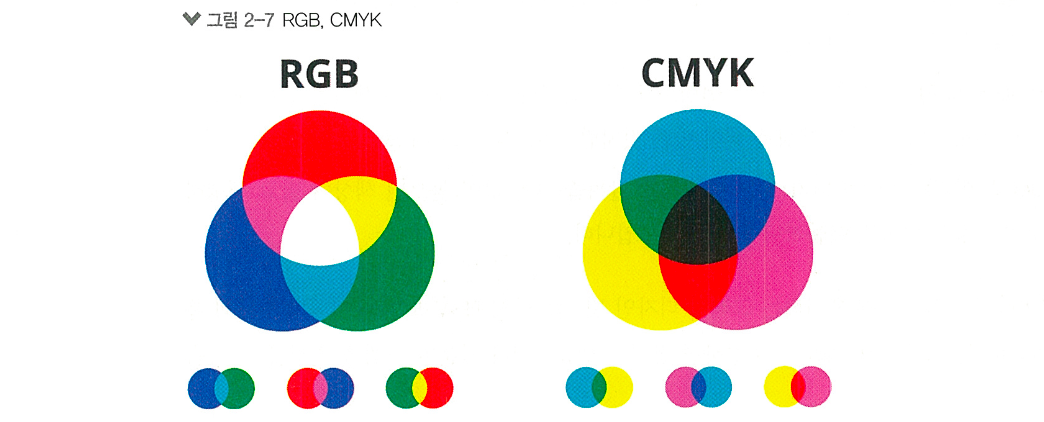
CMYK

인쇄물에 사용되는 색 표현에 대한 다른 접근 방식
빛을 빼는 원리로 작동됨

HSV

Hue(색조):
우리가 보고 있는 색의 유형(R,G,B) 또는 품질을 나타냄

Saturation(채도):
색조의 강도 또는 선명도를 설명

Value(값/밝기):
색상의 밝기, 어두움을 알려줌 (값이 클수록 밝음)

비트

디지털 이미지의 비트 심도
> 이미지의 각 픽셀에 대한 컬러 혹은 그레이 스케일 정보를 표현하는 데 사용되는 비트 수

1비트 --> 0과 1 두 가지 값을 제공

8비트 --> 2^8 = 0~255 사이값. 그레이 스펙트럼

16비트 --> 2^16 = 0~65,535 사이값. 부드러운 색 표현

>> 이미지 품질: 비트 심도가 높을수록 그라데이션이 부드러워짐
>> 파일 사이즈: 비트 심도가 높을수록 파일 사이즈 커짐
>> 편집의 유연성: 비트 심도가 높을수록 이미지 품절 저하 없이 편집 가능
>> 특수 이미징: 의료 영상과 같은 적용에선 디테일 손실이 없게하기 위해 특정 비트 심도가 필요함

2.1.3 이미지에서의 텐서 이해하기

텐서의 이미지 표현

ex) 256x256 사이즈의 그레이 스케일 이미지의 shape = (256, 256)
ex) 256x256 사이즈의 RGB 컬러 이미지의 shape = (256, 256, 3)
ex) 100개 이미지 배치의 256x256 컬러 이미지의 shape = (100, 256, 256, 3)

이미지 다운로드

url = 'https://cobslab.com/wp-content/uploads/2022/02/ai-009-1.jpg'

# 텐서플로의 tf.keras.utils.get_file 함수를 사용하여 지정된 URL에서 이미지 다운로드
# 🚨 TensorFlow 2.11 이후 버전부턴 fname 인자에 파일 이름 넣고, 저장 경로는 따로 cache_dir 인자로 지정 🚨
import tensorflow as tf
image_path = tf.keras.utils.get_file(
    fname='image.jpg',
    origin=url,
    cache_dir='/content'
)

이미지 불러오기

image = tf.io.read_file(image_path)
image

>>> <tf.Tensor: shape=(), dtype=string, numpy=b'\xff\xd8\xff\xe0\x00\ . . . . .
# 파일의 내용은 이미지 변수에 원시 바이너리 문자열로 저장

텐서플로의 decode_jpeg 함수를 사용해서 원시 바이너리 --> 숫자 텐서로 디코딩
channels=3 인수는 컬러 이미지의 R, G, B 채널에 해당하는 3채널 형식으로 이미지 디코딩을 지정
다음 코드로 디코딩된 이미지는 높이, 너비, 색상 채널을 나타내는 3D 텐서로 이미지 변수에 저장됨

# 텐서플로의 tf.image.decode_jpeg 함수를 사용하여 원시 바이너리 문자열을 숫자 텐서로 디코딩
image = tf.image.decode_jpeg(image, channels=3)
image

	# 텐서 객체. 높이 952, 너비 1048, 색상 채널의 개수 3
>>> <tf.Tensor: shape=(952, 1048, 3), dtype=uint8, numpy=
	array([[[ 1, 10, 39],
    	    [ 1, 10, 39],
        	[ 1, 10, 39],
        	...(중략)...
            [ 1, 10, 39],
        	[ 1, 10, 39],
        	[ 1, 10, 39]]], dtype=uint8)>

"""plt.imshow 함수로 이미지 표시"""
import matplotlib.pyplot as plt

plt.imshow(image)
plt.axis('off')
plt.show()

다양한 색 공간으로 작업하기

색 공간의 선택은 컴퓨터 비전 작업의 성능과 정확성에 많은 영향을 줄 수 있음
각 색 공간의 장단점을 이해하는 것이 중요!
채널이 하나뿐인 그레이 스케일 이미지는 계산 효율이 좋고, 모양과 구조 탐지에 성능이 좋음

tf.random.unifrom
tf.random.uniform을 사용하여 랜덤한 값을 가진 텐서를 생성할 수 있음
>> 성능 평가를 위한 임시 이미지를 생성하거나, 시각화 작업에서 색상 패턴 실험에 사용

# 샘플 RGB 이미지
rgb_image = tf.random.uniform([100, 100, 3], maxval=255, dtype=tf.float32)
print(rgb_image)

>>> tf.Tensor(
	[[[172.06085   105.57341   144.46169  ]
 	 [ 34.55243   107.85296    41.10486  ]
 	 [137.8115    110.60343   104.78278  ]
 	 ...(중략)...
     [199.63019   193.30444   235.1837   ]
     [162.5828    173.57964   139.23474  ]
     [203.17017   159.5853    162.96648  ]]], shape=(100, 100, 3), dtype=float32)

# 생성된 이미지 시각화
plt.imshow(rgb_image)
plt.title('RGB Image')
plt.axis('off')
plt.show()

tf.image.rgb_to_grayscale
rgb_to_grayscale을 통해 쉽게 RGB --> 그레이 스케일로 바꿀 수 있음

# 위에서 생성된 RGB 이미지를 그레이 스케일로 변환
grayscale_image = tf.image.rgb_to_grayscale(rgb_image)
print(grayscale_image.shape)

>>> (100, 100, 1)

plt.imshow(grayscale_image.numpy().squeeze(), cmap='gray')
plt.title('Grayscale Image')
plt.axis('off')
plt.show()

tf.image.rgb_to_hsv
rgb_to_hsv는 RGB --> HSV 로 변환하는데 사용

hsv_image = tf.image.rgb_to_hsv(rgb_image)

hue_channel = hsv_image[:,:,0]  # Hue(색조) 채널만 추출

plt.imshow(hue_channel, cmap='hsv')
plt.title('Hue Channel of HSV Image')
plt.axis('off')
plt.colorbar(label='Hue Value')
plt.show()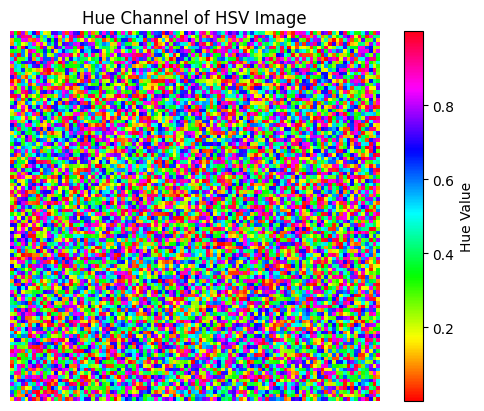

픽셀 값의 정규화와 표준화

이미지 처리에서 픽셀 값의 사이즈를 조정하는 건 모델의 성능과 속도에 많은 영향을 끼침
픽셀 값의 사이즈를 조정하는 데 사용되는 두 가지 대표적 방법은 정규화, 표준화

정규화
>> 픽셀 값을 [0, 1] 범위로 스케일링하는 과정
ex) rgb_image 텐서를 255로 나누면 자동으로 '브로드캐스트'하여 각각의 텐서에 동일한 연산을 함

normalized_image = rgb_image / 255.0
rgb_image[0][0] , normalized_image[0][0]

>>> (<tf.Tensor: shape=(3,), dtype=float32, numpy=array([231.48172, 235.72926, 213.58714], dtype=float32)>,
 	 <tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.90777147, 0.92442846, 0.83759665], dtype=float32)>)

표준화
>> 픽셀 값을 평균 = 0, 표준 편차 = 1 이 되도록 스케일링하는 과정
최적화 환경을 균일하게 만들어 학습을 빠르게 함. 중요한 전처리 단계!
픽셀 값을 표준화하면 중앙이 0이 되고, 대략 [-1, 1] 범위에 속하게 되어 일관된 훈련 데이터 제공 가능

mean = tf.reduce_mean(rgb_image)  # 평균값 계산
stddev = tf.math.reduce_std(rgb_image)  # 표준 편차 계산

standardized_image = (rgb_image - mean) / stddev  # 표준화
rgb_image[0][0] , standardized_image[0][0]

>>> (<tf.Tensor: shape=(3,), dtype=float32, numpy=array([231.48172, 235.72926, 213.58714], dtype=float32)>,
 	 <tf.Tensor: shape=(3,), dtype=float32, numpy=array([1.415816 , 1.4735496, 1.1725885], dtype=float32)>)

2.2 이미지 처리 기법

2.2.1 이미지 필터링

선명함을 드러내고, 노이즈에서 사용자가 원하는 값을 추출하는 것이 목표!
이러한 작업을 해주는 이미지 필터는 커널(kernal)이라는 이름으로 불리기도 함

선형 필터와 비선형 필터

>> 필터는 이미지를 텐서로 변환하고, 텐서의 좌측 상단부터 우측 하단으로 이동하며 연산을 진행함

선형 필터
픽셀을 필터 처리할 때 나온 결과 픽셀 값이, 입력으로 들어왔던 이웃 픽셀 값의 가중치 합이 됨
>> 선형 필터는 항상 고정되고 예측 가능한 방식으로 픽셀 값을 결합함

비선형 필터
출력이 입력 값의 순위/순서 또는 기타 비선형 연산에 따라 달라짐
>> 고정된 방식으로 값을 결합하는 것이 아니라, 특정 조건이나 규칙에 따라 값을 선택/변경할 수 있음
ex) 중앙 값 필터링 기법

중앙 값 필터링

중앙 값 필터의 핵심은 비선형 디지털 필터링 기법
주요 목적은 노이즈 감소, 특히 흰색/검은색 픽셀들인 소금과 후추 노이즈를 줄이는 것!

>> 이미지의 각 픽셀에 대해 주변을 고려하고 해당 주변에서 강도 값의 중앙 값을 결정한 다음,
해당 픽셀의 값을 이 중앙 값으로 대체하는 개념

"""임의의 사진에 노이즈를 첨가"""
import numpy as np
import cv2

# 소금(흰색) 노이즈 생성 함수
def generate_salt_noise(image):
    num_salt = np.ceil(0.05 * image.size)
    coords = [np.random.randint(0, i - 1, int(num_salt))
              for i in image.shape]
    salted_image = image.copy()
    salted_image[coords[0], coords[1]] = 255
    return salted_image

# 후추(검은색) 노이즈 생성 함수
def generate_pepper_noise(image):
    num_pepper = np.ceil(0.05 * image.size)
    coords = [np.random.randint(0, i - 1, int(num_pepper))
              for i in image.shape]
    peppered_image = image.copy()
    peppered_image[coords[0], coords[1]] = 0
    return peppered_image

"""노이즈 생성 & 중앙값 필터 적용 후 시각화"""
!wget https://raw.githubusercontent.com/Cobslab/imageBible/main/image/like_lenna.png
lenna_image = cv2.imread('like_lenna.png', cv2.IMREAD_GRAYSCALE)

salted_lenna = generate_salt_noise(lenna_image)
peppered_lenna = generate_pepper_noise(salted_lenna)
filtered_lenna = cv2.medianBlur(peppered_lenna, 5)


fig, axes = plt.subplots(1, 4, figsize=(20, 6))

import matplotlib.pyplot as plt

axes[0].imshow(lenna_image, cmap='gray')
axes[0].set_title('Original Lenna Image')
axes[0].axis('off')

axes[1].imshow(salted_lenna, cmap='gray')
axes[1].set_title('Salted Lenna Image')
axes[1].axis('off')

axes[2].imshow(peppered_lenna, cmap='gray')
axes[2].set_title('Salted & Peppered Lenna')
axes[2].axis('off')

axes[3].imshow(filtered_lenna, cmap='gray')
axes[3].set_title('Median Filtered Lenna')
axes[3].axis('off')

plt.tight_layout()
plt.show()

>> 확실히 노이즈가 사라졌지만, 필터링된 이미지는 원본 이미지에 비해 화질이 흐려짐
중앙 값 필터는 에지와 가장자리를 보존함. = (선명도 유지)
이는 중앙 값이 평균에 비해 이상치를 처리하는 데 더 우수한 지표이기 때문

적용 사례
의료: 의료 영상에서 가장 중요한 것은 "선명도"이기 때문에 중앙 값 필터링이 도움이 됨
천체 영상: 우주 이미지는 우주선 간섭으로 밝은 노이즈가 발생하기에 선명도 손상없이 도움이 됨

가우시안 필터링

가우시안 필터링의 핵심은 이미지에 블러 효과를 부여하는 방법!
'균일한 스무딩' 효과를 적용하는 다른 블러링 방법과 달리,
가우시안 필터는 '멀리 있는 픽셀보다 가까운 픽셀을 강조'하여 시각적으로 돋보이게 함

가우스 함수

1차원 \;가우스 함수: \quad G(x) = \frac {1}{\sqrt {2\pi\sigma}}e^{-\frac {x^2}{2\sigma^2}}

2차원 \;가우스 함수: \quad G(x,y) = \frac {1}{\sqrt {2\pi\sigma}}e^{-\frac {x^2+y^2}{2\sigma^2}}

$\sigma$ 는 표준편차이며, 가우스 함수의 확산 정도를 결정함.
$\sigma$ 가 클수록 확산 범위가 넓어져 흐림 효과가 강해지고, 작을수록 흐림이 국소적으로 적용돼 섬세해짐.

블러링이 유일한 용도는 아님!
- 노이즈 감소: 픽셀의 무작위 변동을 흐리게 해 노이즈를 줄일 수 있음
- 가장자리 감지를 위한 사전 처리: 에지를 감지하기 전에 가우시안을 적용하면 에지 변화를 부드럽게 함

뿌옇게 처리하는게 어떻게 노이즈 감소 방법이 되는건지?
>> "노이즈"란 원래 없어야 할, 갑자기 튀는 이상한 픽셀 값들.
"뿌옇게 처리"는 픽셀 값이 주변 환경과 비슷하게 맞춰지는 것.
즉, 가우시안 필터를 적용하면 주변과 평균되며 튀는 값이 완화됨.

"""이미지 불러온 후 무작위 노이즈 첨가"""
import cv2
import numpy as np
import matplotlib.pyplot as plt

image = cv2.imread('like_lenna.png', cv2.IMREAD_GRAYSCALE)  # 그레이 스케일 이미지 읽어오기
mean = 0
sigma = 1
gaussian_noise = np.random.normal(mean, sigma, image.shape).astype('uint8')
noisy_image = cv2.add(image, gaussian_noise)

plt.imshow(noisy_image, cmap='gray')
plt.title('Noisy Image')
plt.axis('off')
plt.show()

"""가우시안 필터 적용하여 뿌옇게 처리"""
sigma_values = [1, 5, 10]
denoised_images = []

for sigma in sigma_values:
    denoised = cv2.GaussianBlur(noisy_image, (0, 0), sigma)  # Kernel size computed from sigma
    denoised_images.append(denoised)

fig, axes = plt.subplots(1, 4, figsize=(20, 10))

axes[0].imshow(noisy_image, cmap='gray')
axes[0].set_title('Noisy Image')
axes[0].axis('off')

for ax, img, sigma in zip(axes[1:], denoised_images, sigma_values):
    ax.imshow(img, cmap='gray')
    ax.set_title(f'Denoised (σ={sigma})')
    ax.axis('off')

plt.tight_layout()
plt.show()

$\sigma$ 값에 따라 이미지가 흐려질수록 노이즈는 사라짐
이미지 사이즈나 품질에 따라 적절한 시그마 값을 적용하여 사용

2.2.2 이미지 변환

>> 이미지의 시각적 정보를 다른 형태로 재해석하거나 조정하여 특정 목적을 달성하는 것이 목표

아핀 변환

라틴어 아피니스("연결된")에서 유래
점과 점 사이의 기본 관계를 변경하지 않고 개체의 기하학적 속성을 변경할 수 있는 변환

특징

점과 선의 보존 - 변환 전에 세 점이 같은 선상에 있었다면 변환 후에도 유지됨
평행성 - 변환 전에 평행했던 선은 변환 후에도 유지됨
평면 관계 - 변환 전에 여러 점이 같은 평면에 놓여 있었다면 변환 후에도 유지됨
아핀 변환의 구성 - 아핀 변환을 여러번 적용해도 위 특징은 유지됨

"""실습을 위한 원본이미지"""
import cv2
import numpy as np
import matplotlib.pyplot as plt

image_path = "like_lenna.png"
img = cv2.imread(image_path)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)  # 📌 기본값은 BGR임. RGB로 변환해주기 📌
plt.imshow(img)
plt.title("Original Image")
plt.show()

회전 변환
아핀 변환 중 회전을 진행해보자. 중심을 기준으로 각도를 주어 회전됨.

"원점을 기준으로 회전할때"

회전행렬: \quad \begin{pmatrix}cos(\theta)&-sin(\theta)\\sin(\theta)&cos(\theta)\\ \end{pmatrix}\begin{pmatrix}x\\y\\ \end{pmatrix}

를 바로 적용하고,

"다른 점(c)를 기준으로 회전할때"

x' = x_1 + c_x\\ y' = y_1 + c_y

와 같은 평행이동을 해준 후에 위의 '회전행렬'을 적용해 회전시킴

def rotate_image(image, angle, center=None):
    rows, cols, _ = image.shape
    if center is None:
        center = (cols // 2, rows // 2)
    M = cv2.getRotationMatrix2D(center, angle, 1)  # 회전행렬을 만들어줌!
    rotated = cv2.warpAffine(image, M, (cols, rows))
    return rotated

rotated_img = rotate_image(img, 45)  # 중심축을 기준으로 45도 회전
plt.imshow(rotated_img)
plt.title("Rotated Image")
plt.show()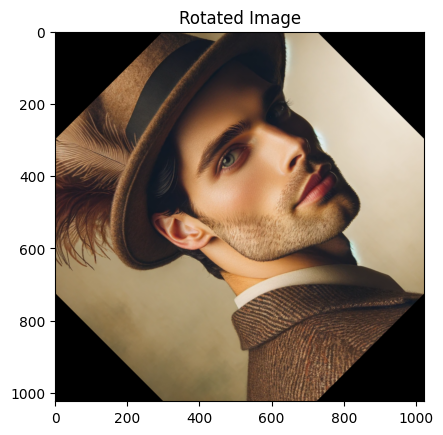

원근 변환

원근 변환의 핵심은 호모그래피 행렬을 사용하는 것!
호모그래피 행렬은 소스 이미지의 점 4개와 대상 이미지의 점 4개를 사용하여 계산되는데,
이 행렬은 소스 이미지의 각 픽셀에 대해 새로운 좌표를 계산해서 이미지를 변환함.
>> 이 변환으로 이미지의 원근이 수정되어 대상 이미지에 맞게 보이게 됨

from matplotlib import pyplot as plt
import cv2
import numpy as np

!wget https://raw.githubusercontent.com/Lilcob/test_colab/main/perspective_test.jpg

# 이미지 로드
image_path = 'perspective_test.jpg'
new_source_image = cv2.imread(image_path)

# 이미지에서 타겟의 꼭지점 좌표 지정 (좌표 순서 변경)
ordered_corners = np.array([[57, 630], [936, 330], [1404, 792], [550, 1431]], dtype='float32')

# 너비와 높이 계산
ordered_width = int(max(np.linalg.norm(ordered_corners[0] - ordered_corners[1]),
                        np.linalg.norm(ordered_corners[2] - ordered_corners[3])))
ordered_height = int(max(np.linalg.norm(ordered_corners[0] - ordered_corners[3]),
                         np.linalg.norm(ordered_corners[1] - ordered_corners[2])))

# 변환이 될 꼭지점 좌표 지정
ordered_rect_corners = np.array([[0, 0], [ordered_width, 0], [ordered_width, ordered_height], [0, ordered_height]], dtype='float32')

# 호모그래피 행렬 계산
ordered_scan_matrix = cv2.getPerspectiveTransform(ordered_corners, ordered_rect_corners)

# 원근 변환 다시 적용
ordered_scanned_image = cv2.warpPerspective(new_source_image, ordered_scan_matrix, (ordered_width, ordered_height))

# 스캔된 이미지 다시 출력
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.title("New Source Image")
plt.imshow(cv2.cvtColor(new_source_image, cv2.COLOR_BGR2RGB))
plt.subplot(1, 2, 2)
plt.title("Ordered Scanned Image")
plt.imshow(cv2.cvtColor(ordered_scanned_image, cv2.COLOR_BGR2RGB))
plt.show()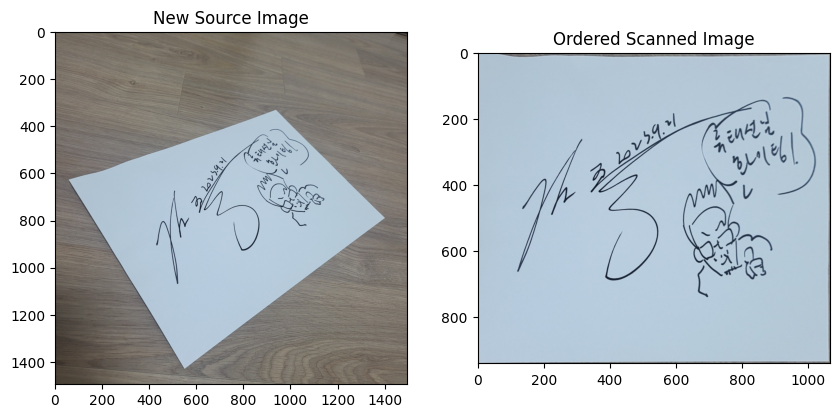

2.2.3 주파수 도메인 기법

푸리에 변환

F(t) = \int_{-\infin}^{\infin}{f(t)e^{-j2\pi f(t)}dt}

$f(t)$ : 시간 도메인 신호 함수
$e^{-j2\pi f(t)}$ : 복소 지수 함수. 푸리에 변환의 주파수 성분을 분해하는 데 사용
$f$ : 주파수 변수

2.2.4 이미지 경계 검출

Changh2

Shoot for the moon! 🔥

이전 포스트

[이미지처리바이블] 1장 기본 개념과 도구

다음 포스트

[이미지처리바이블] 2장 이미지 처리 기초