[이미지처리바이블] 3.1장 딥러닝이란?

Changh2·2025년 3월 25일

Computer Vision Image Processing 이미지처리 컴퓨터비전

이미지처리바이블

목록 보기

3/7

[이미지 처리 바이블] 교재 3장을 기반으로 작성되었습니다.

3.1 딥러닝이란?

3.1.1 인공 신경망 기초

인공지능과 이미지 처리의 관계

인공지능 기술이 발전해감에 따라 이미지 처리에도 수많은 기법이 추가됨

딥러닝: 인공지능의 한 분야. 인간의 뇌처럼 데이터를 처리/학습

이미지 처리의 한계

*CIFAR-10: 컴퓨터 비전 인공지능 모델의 성능을 평가하는 벤치마크 데이터 세트

사람은 레이블을 확인하지 않아도 각 이미지가 무엇을 나타내는지 쉽게 알 수 있음
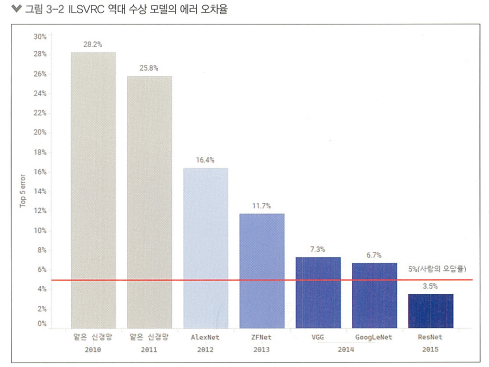
프로그램으로는 처리하기 어려우므로, 컴퓨터 비전 대회 ILSVRC(ImageNet Large Scale Visual Recognition Challenge)를 2010년부터 2017년까지 이어가며 인공지능의 발전을 이끔

인공지능 모델의 발전

2012년 AlexNet이라는 깊은 구조의 신경망 모델이 ILSVRC에서 우승하며 인공지능 모델의 발전에 큰 변화를 가져옴
이후, GoogLeNet 모델, ResNet 모델 등이 깊이와 너비를 늘려 모델의 성능을 향상시킴

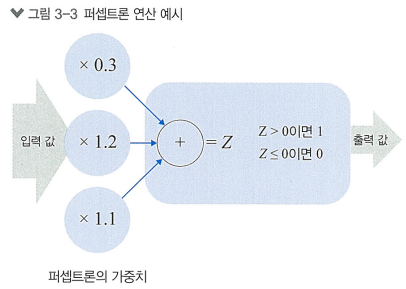
퍼셉트론

> 아주 간단한 형태의 인공 신경망.
여러 개의 입력 값을 받아 이들의 가중합을 계산하고, 활성화 함수를 적용하여 출력 값 생성

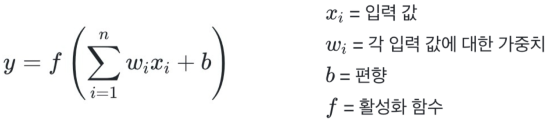
비용 함수

퍼셉트론은 *델타 규칙에 따라 학습됨
*델타 규칙: 출력 값과 실제 정답과의 오차에 따라 가중치를 조절하는 기법

>> 이 오차를 정의하는 것이 비용 함수이고, 이를 통해 모델의 성능을 평가함 (값이 클 수록 오차가 큰 것)

AND, OR, NOR 연산


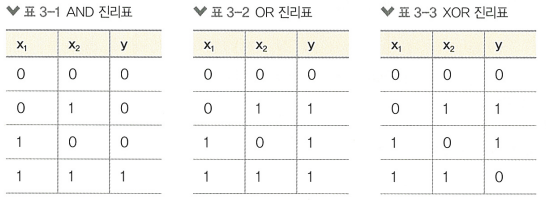
"""위의 세 진리표를 텐서플로의 텐서 데이터로 만듬"""

import tensorflow as tf

x1 = [0,0,1,1]
x2 = [0,1,0,1]
x = tf.transpose(tf.constant([x1,x2],dtype=tf.float32))

and_y = tf.constant([0,0,0,1],dtype=tf.float32)
or_y = tf.constant([0,1,1,1],dtype=tf.float32)
xor_y = tf.constant([0,1,1,0],dtype=tf.float32)

print(f"x: \n{x}")
print(f"AND y:\t{and_y}",f"OR  y:\t{or_y}",f"XOR y:\t{xor_y}",sep="\n")

>>> x: 
	[[0. 0.]
 	[0. 1.]
 	[1. 0.]
 	[1. 1.]]
	AND y:	[0. 0. 0. 1.]
	OR  y:	[0. 1. 1. 1.]
	XOR y:	[0. 1. 1. 0.]

"""그래프로 표현"""

import matplotlib.pyplot as plt
import seaborn as sns

sns.set_style("darkgrid")
fig, axs = plt.subplots(1, 3, figsize=(15, 5))

# AND 문제
sns.scatterplot(x=x[:, 0], y=x[:, 1], hue=and_y, ax=axs[0])
axs[0].set_title("AND Problem")
axs[0].set_xlabel("X1")
axs[0].set_ylabel("X2", rotation=0)

# OR 문제
sns.scatterplot(x=x[:, 0], y=x[:, 1], hue=or_y, ax=axs[1])
axs[1].set_title("OR Problem")
axs[1].set_xlabel("X1")
axs[1].set_ylabel("X2", rotation=0)

# XOR 문제
sns.scatterplot(x=x[:, 0], y=x[:, 1], hue=xor_y, ax=axs[2])
axs[2].set_title("XOR Problem")
axs[2].set_xlabel("X1")
axs[2].set_ylabel("X2", rotation=0)
plt.tight_layout()
plt.show()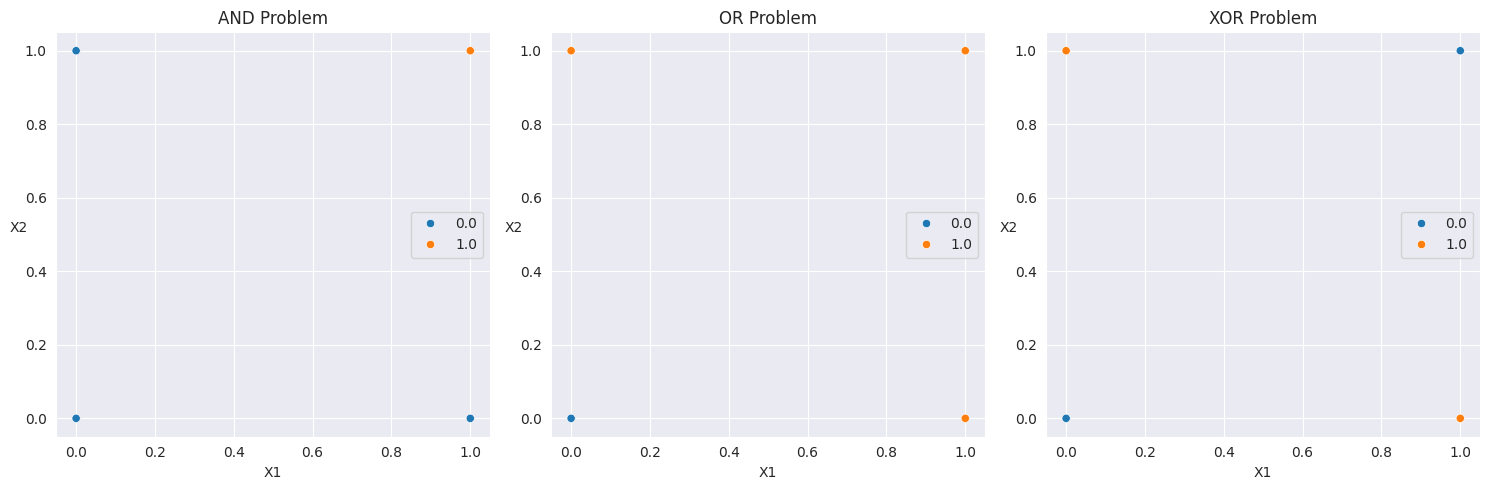

퍼셉트론

퍼셉트론이 어떻게 학습하여 위의 문제를 해결하는지 봐보자.

# MLP 모델 정의
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(1, input_dim=2, activation='sigmoid')  # 활성화 함수로 시그모이드 사용
])

시그모이드 함수 : \quad \sigma (x) = \frac {1}{1+e^{-x}}

"""AND 연산을 해결하기 위한 학습"""
# AND 연산
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=1.0),
              loss='binary_crossentropy',
              metrics=['accuracy'],)

model.fit(x, and_y, epochs=100, batch_size=4)

# 모델 평가
loss, accuracy = model.evaluate(x, and_y)
print(f'Loss: {loss}, Accuracy: {accuracy}')

# 예측
predictions = model.predict(x)
print(f'Predictions:\n{predictions}')

>>> Epoch 1/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 2s 2s/step - accuracy: 0.7500 - loss: 0.8009
	Epoch 2/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 465ms/step - accuracy: 0.7500 - loss: 0.7638
	Epoch 3/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 55ms/step - accuracy: 0.7500 - loss: 0.7295
    ...(중략)...
    Epoch 99/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 54ms/step - accuracy: 1.0000 - loss: 0.1496
	Epoch 100/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step - accuracy: 1.0000 - loss: 0.1485
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 293ms/step - accuracy: 1.0000 - loss: 0.1473
	Loss: 0.1473318189382553, Accuracy: 1.0
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 120ms/step
	Predictions:
	[[0.00911525]
 	[0.1524532 ]
 	[0.15414722]
 	[0.78086656]]
    
# 금방 정답률이 1에 도달하고, Predictions의 각 근사치가 AND 연산의 결과와 동일함

"""OR 연산을 해결하기 위한 학습"""
# OR 연산
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(1, input_dim=2, activation='sigmoid')
])

model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=1.0),
              loss='binary_crossentropy',
              metrics=['accuracy'])

model.fit(x, or_y, epochs=100, batch_size=4)

loss, accuracy = model.evaluate(x, or_y)
print(f'Loss: {loss}, Accuracy: {accuracy}')

predictions = model.predict(x)
print(f'X:\n{x}')
print(f'Predictions:\n{predictions}')

>>> Epoch 1/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 576ms/step - accuracy: 0.5000 - loss: 0.9692
	Epoch 2/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 143ms/step - accuracy: 0.5000 - loss: 0.7042
	Epoch 3/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - accuracy: 0.5000 - loss: 0.5838
	...(중략)...
	Epoch 99/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step - accuracy: 1.0000 - loss: 0.0933
	Epoch 100/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 60ms/step - accuracy: 1.0000 - loss: 0.0924
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 216ms/step - accuracy: 1.0000 - loss: 0.0916
	Loss: 0.09159894287586212, Accuracy: 1.0
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 95ms/step
	X:
	[[0. 0.]
	 [0. 1.]
	 [1. 0.]
	 [1. 1.]]
	Predictions:
	[[0.19059952]
	 [0.9221345 ]
	 [0.9301786 ]
	 [0.9985097 ]]

# 금방 정답률이 1에 도달하고, Predictions의 각 근사치가 OR 연산의 결과와 동일함

하지만, XOR 연산은 해결할 수 없음!

"""XOR 연산을 해결하기 위한 학습"""
# XOR 연산
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(1, input_dim=2, activation='sigmoid')
])

model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=1.0),
              loss='binary_crossentropy',
              metrics=['accuracy'])

model.fit(x, xor_y, epochs=100, batch_size=4)

loss, accuracy = model.evaluate(x, xor_y)
print(f'Loss: {loss}, Accuracy: {accuracy}')

predictions = model.predict(x)
print(f'X:\n{x}')
print(f'Predictions:\n{predictions}')

>>> Epoch 1/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 451ms/step - accuracy: 0.7500 - loss: 0.7563
	Epoch 2/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 148ms/step - accuracy: 0.5000 - loss: 0.7375
	Epoch 3/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step - accuracy: 0.5000 - loss: 0.7276
	...(중략)...
	Epoch 99/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 50ms/step - accuracy: 0.5000 - loss: 0.6931
	Epoch 100/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step - accuracy: 0.5000 - loss: 0.6931
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 215ms/step - accuracy: 0.5000 - loss: 0.6931
	Loss: 0.6931484937667847, Accuracy: 0.5
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 95ms/step
	X:
	[[0. 0.]
 	[0. 1.]
 	[1. 0.]
 	[1. 1.]]
	Predictions:
	[[0.50129217]
 	[0.49989906]
 	[0.5005066 ]
 	[0.4991134 ]]
    
# XOR 문제를 만나면 정답률이 50% 정도로, 0과 1을 판단하지 못함!!

페셉트론으론 해결 못하는 XOR 연산을 해결하기 위한 딥러닝의 등장하는 과정으로 다층 퍼셉트론이 도입됨

다층 퍼셉트론

> 여러 개의 퍼셉트론 층을 사용해 XOR과 같은 비선형적인 문제를 해결함.
복잡해진 모델을 최적화하기 위해선 다음과 같은 과정을 거침

1. 순전파
현재의 매개변수 $\theta$ 를 사용해 입력 $x$ 를 전달, 출력 생성

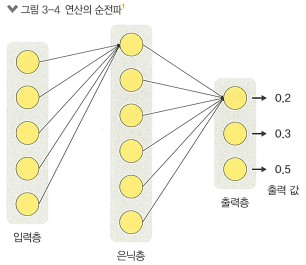
2. 손실 계산
   네트워크의 출력과 실제 정답 사이의 오차를 계산해 손실 $L(X, \theta)$ 를 얻음
3. 역전파
   손실 함수에 대한 그레디언트를 계산하기 위해 역전파 알고리즘 사용.
   이 단계에서는 각 매개변수에 대한 손실 함수의 편미분을 계산함

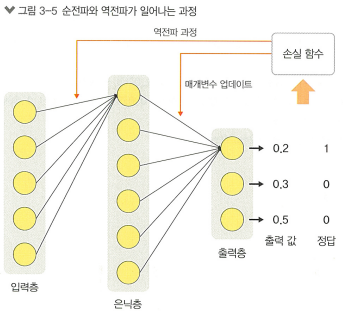
4. 매개변수 업데이트
계산된 그레디언트를 사용해 매개변수를 업데이트함.

ex) 경사 하강법 사용해서 손실함수가 최소가 되는 방향으로 매개변수 조정

"""XOR 연산을 해결하기 위한 학습"""
model = tf.keras.models.Sequential([  # 2개의 밀집층을 가짐
    tf.keras.layers.Dense(16, input_dim=2, activation='relu'),	# 2개의 데이터를 16개의 퍼셉트론에 대입,
    tf.keras.layers.Dense(1, activation='sigmoid')				# 다시 1개의 퍼셉트론에 대입 (relu 활성화함수로 비선형성 도입)
])

model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=1),
              loss='binary_crossentropy',
              metrics=['accuracy'])

model.fit(x, xor_y, epochs=100, batch_size=4)

loss, accuracy = model.evaluate(x, xor_y)
print(f'Loss: {loss}, Accuracy: {accuracy}')

predictions = model.predict(x)
print(f'X:\n{x}')
print(f'Predictions:\n{predictions}')

>>> Epoch 1/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 1s/step - accuracy: 0.7500 - loss: 0.6857
	Epoch 2/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - accuracy: 0.5000 - loss: 0.6734
	Epoch 3/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - accuracy: 0.7500 - loss: 0.6594
	...(중략)...
	Epoch 99/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step - accuracy: 1.0000 - loss: 0.0291
	Epoch 100/100
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step - accuracy: 1.0000 - loss: 0.0286
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 287ms/step - accuracy: 1.0000 - loss: 0.0282
	Loss: 0.02817685529589653, Accuracy: 1.0
	1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 141ms/step
	X:
	[[0. 0.]
	 [0. 1.]
	 [1. 0.]
	 [1. 1.]]
	Predictions:
	[[0.07319723]
 	[0.9841941 ]
 	[0.986696  ]
 	[0.00734043]]
    
# 2개의 밀집층을 쌓아 XOR 연산을 해결함!

활성화 함수

> 복잡한 비선형 문제도 해결할 수 있는 능력을 갖게 해줌

초기엔 계단함수를 사용했지만, 모델이 학습을 하는 과정에서 오차 값을 줄이기 위해 "미분"의 개념인 그레디언트를 사용한다는 수학적 문제에 부딪힘.
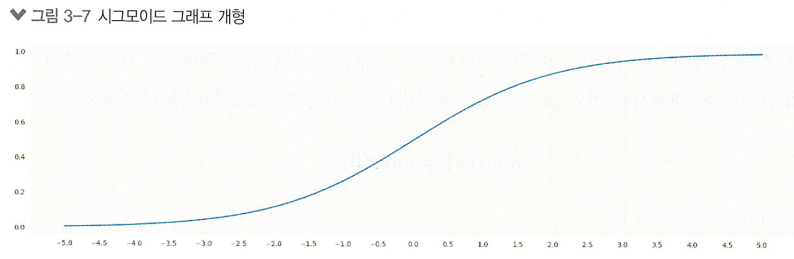
그렇기에 부드럽게 변화하는 그래프를 갖는 시그모이드 함수를 사용함
시그모이드 함수는 0 ~ 1 사이값을 도출함

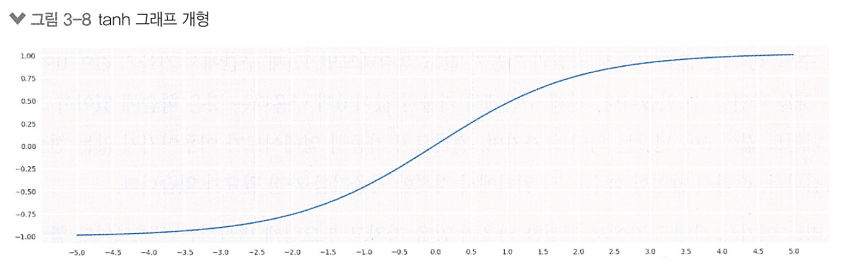
tanh
tanh함수는 -1 ~ 1 사이값을 도출함

tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}

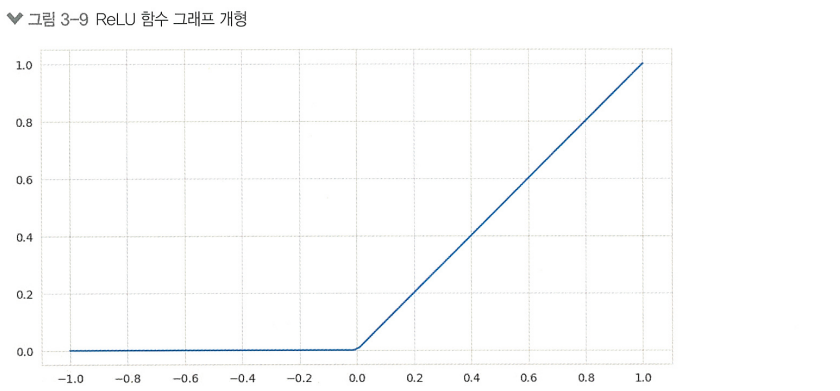
ReLU
최근 가장 널리 사용 되는 활성화 함수 ReLU(Rectified Linear Unit)
> 간단한 수학적 표현으로 연산속도가 빠르고,
> 비선형성을 유지하며 선형 함수의 성질도 일부 유지하고,
> 기울기 소실 문제를 어느정도 해결해줌

ReLU(x) = max(0,x)

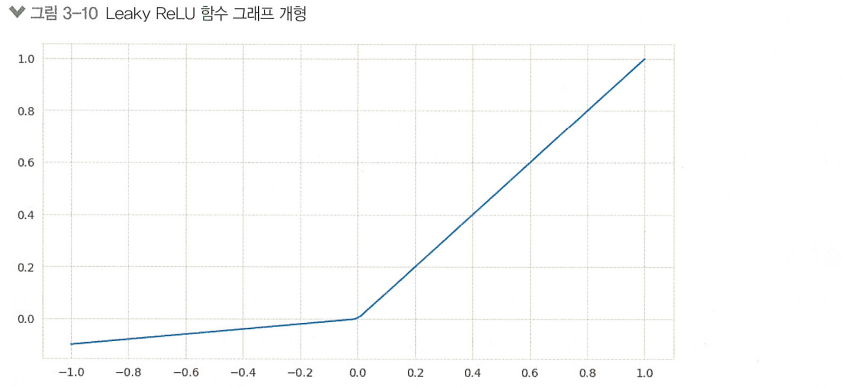
Leaky ReLU
ReLU 뉴런이 학습의 어느 순간부터 항상 0을 출력하게 되는 현상인 '죽은 ReLU' 문제를 막기위함

Leaky ReLU(x) = max(0.1,x)

소프트맥스
"다중 클래스 분류" 문제에서 "출력층"의 활성화 함수로 사용
각 클래스에 대한 점수를 받아서 확률 분포로 변환함

softmax(x_i) = \frac {e^{x_i}}{\sum_{j=1}^C e^{x_j}}

손실 함수

평균 제곱 오차
주로 "회귀" 문제에 사용. 실제 값과 예측 값의 차이를 제곱하여 평균함
( $y_i$ 는 실제 정답 데이터, $\hat y_i$ 는 모델이 예측한 예측 값)

L_{\text{mse}} = \frac{1}{n} \displaystyle\sum_{i=1}^{n} (y_i - \hat y_i)^2

이진 교차 엔트로피
"이진 분류" 문제에서 사용. 실제 레이블과 예측 확률 사이의 차이를 측정함
( $N$ 은 데이터 세트의 샘플 수, $y_i$ 는 $i$ 번째 샘플 $x_i$ 의 실제 레이블(0 또는 1), $P$ 는 $x_i$ 에 대해서 모델이 예측해본 예측 확률)

L_{\text{binary-cross entropy}}(x) = -\frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(P(x_i)) + (1 - y_i) \log(1 - P(x_i)) \right]

교차 엔트로피
"분류" 문제에 주로 사용. 실제 클래스의 레이블과 모델이 예측한 확률 분포 사이의 차이를 측정함
( $C$ 는 예측하려는 범주의 총 개수, $q$ 는 예측하려고 하는 실제 대상들의 확률 분포, $p$ 는 예측 모델의 결과로서 반환되는 확률 함수)

L_{\text{cross entropy}}(\mathbf{y}, \hat{\mathbf{y}}) = -\sum_{i=1}^{c} \left[ q(y_i) \log(p(\hat{y}_i)) \right]

모델 최적화

> 모델의 가중치와 편향 값을 (손실 함수의 값을 최소화하기 위해) 업데이트하는 방법을 포함함

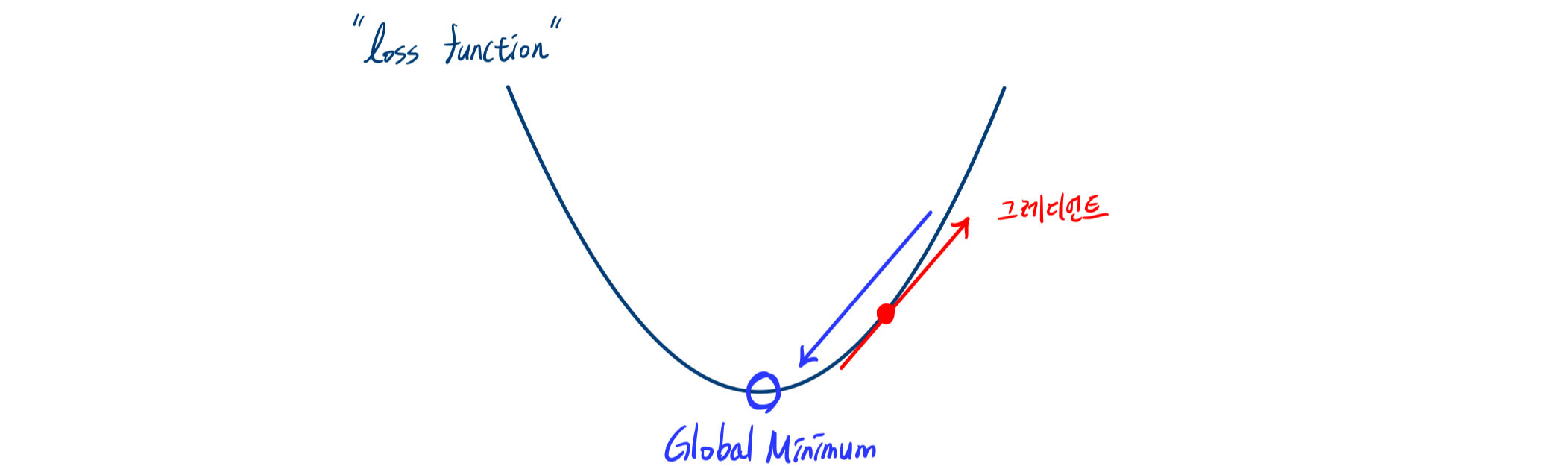
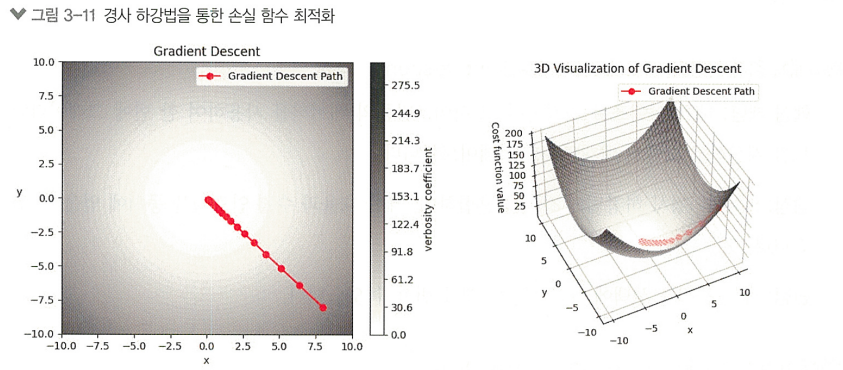
경사 하강법
손실함수의 기울기(그레디언트)를 계산하여, 그 반대 방향으로 조금씩 업데이트함으로써
손실 함수의 값이 최소가 되는 지점을 찾음

확률적 경사 하강법(SGD, Stochastic Gradient Descent)
> 훈련 세트 중 딱 하나의 샘플을 랜덤하게 뽑아 그 학습 데이터만을 사용하여 그레디언트를 계산, 매개변수 업데이트

미니배치 경사 하강법
> 훈련 세트에서 일정한 배치 사이즈 만큼의 데이터를 꺼내 사용하여 한 번에 그레디언트를 계산, 매개변수 업데이트

RMSprop(Root Mean Square Propagation)
> 미니 배치 경사 하강법의 확장
> 학습률을 적응적으로 조정하여 학습 과정을 안정화시킴

Adam(Adaptive Moment Estimation)
> 모멘텀과 RMSprop의 아이디어를 합쳐 그레디언트의 1차 모멘트(평균)와 2차 모멘트(분산)를 추정하여 매개변수 업데이트

+) 모멘텀이란?

인공지능 모델의 설계 및 학습

선형 회귀를 실습해보기 위해 텐서플로를 사용해 임의 데이터 세트를 만들어보자

데이터 세트의 구조

선형 회귀를 위해 아래와 같이 선형 관계를 정의함

Y = 1.5X + 3

위 수식에서 기울기(1.5)와 절편(3)은 2차원 공간에서 직선을 정의하는 "매개변수"이다. (매개변수 업데이트)

임의의 독립 변수 X값 생성

import tensorflow as tf

x = tf.random.uniform(shape=[100], minval=1, maxval=4)  # 100개의 무작위 값 생성
print(x)

>>> tf.Tensor(
	[2.372521  2.6322994 3.5555437 3.9232826 1.3707356 3.2020717 1.9272035
	 2.8056293 3.2508655 2.6148477 2.3290071 3.668225  3.1298292 3.8164668
     ...(중략)...
	 3.8406534 2.90824   3.6569834 2.2526617 1.9518126 2.2392645 2.2504907
	 2.65007   2.5888472], shape=(100,), dtype=float32)

선형 관계가 있는 종속 변수 Y값 생성

slope = 1.5
intercept = 3
epsilon = tf.random.truncated_normal(shape=[100], mean=0, stddev=0.3)
y = slope * x + intercept + epsilon  # 위의 수식에서 정의한 선형 관계
print(y)

>>> tf.Tensor(
	[6.74476   7.2772617 8.622717  9.045624  5.0619035 7.6717353 5.905293
	 7.0692835 7.927641  6.5626116 6.4334044 8.029643  7.4742274 8.898156
	 ...(중략)...	
	 8.803744  7.1300993 8.702858  6.7209067 5.7525964 6.617983  6.2661033
	 6.777974  6.8323107], shape=(100,), dtype=float32)

Matplotlib을 사용한 데이터 시각화

import matplotlib.pyplot as plt
import seaborn as sns

sns.set_style("darkgrid")
plt.scatter(x, y)
plt.xlabel('Feature (X)')
plt.ylabel('Label (Y)')
plt.title('sythetic dataset')
plt.show()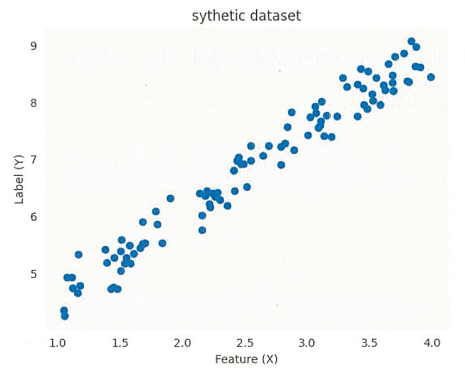

선형 데이터 모델링

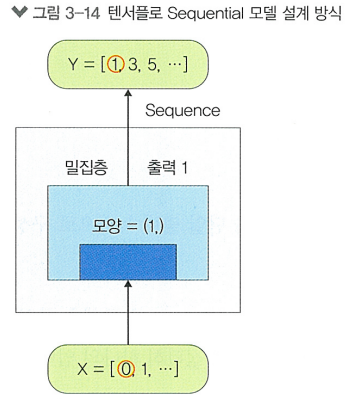
모델 설계

"""Sequential 모델: 한번에 하나의 층을 추가하여 쉽게 구축할 수 있는 선형층 스택"""
from tensorflow.keras import Sequential 

"""Dense층: 신경망에서의 뉴런 밀집층"""
from tensorflow.keras.layers import Dense

model = Sequential()  # 시퀀셜 모델 초기화
model.add(Dense(1, input_shape=(1,)))  # 모델에 밀집층 추가
"""
밀집층의 첫 번째 인수 1 == 층에 있는 뉴런의 수 == 입력값을 받아 계산을 해주는 수식의 수 ❗❗
input_shape=(1,) 부분의 인수는 입력 데이터의 모양을 지정
"""

model.compile(loss='mean_squared_error', optimizer='sgd')  
# 손실 함수와 최적화 함수 지정, 모델 컴파일

모델 학습

"""
입력이 (1,) 모양을 가질 것으로 예상되므로 X 텐서의 모양이 호환되는지 확인
(-1, 1) 에서 -1은 해당 차원의 사이즈를 텐서플로가 유추하도록 해줌 
>> 100개의 요소를 가진 1차원 텐서면 (100, 1)이 됨
"""
x_train = tf.reshape(x, (-1, 1))  
x_train.shape

>>> TensorShape([100, 1])

"""모델 학습 진행"""
history = model.fit(x_train, y, epochs=300)

>>> Epoch 1/300
	4/4 [==============================] - 1s 4ms/step - loss: 40.4873
	Epoch 2/300
	4/4 [==============================] - 0s 3ms/step - loss: 10.9472
	Epoch 3/300
	4/4 [==============================] - 0s 3ms/step - loss: 2.9398
	...(중략)...
	Epoch 299/300
	4/4 [==============================] - 0s 3ms/step - loss: 0.0652
	Epoch 300/300
	4/4 [==============================] - 0s 4ms/step - loss: 0.0659

"""적절한 기울기, 절편을 찾았는지 확인"""
weights, bias = model.get_weights()
print("Weights (Slope):", weights)
print("Bias (Intercept):", bias)

>>> Weights (Slope): [[-1.0370896]]
	Bias (Intercept): [0.]

3.1.2 합성곱 신경망(CNN)

이미지를 위와 같은 선형 신경망 모델로 처리하게 되면,
이미지 데이터가 갖는 공간 정보가 소실되고, 모든 픽셀 간 연산이 이루어져 연산량이 지나치게 많아짐!
>> CNN이 이를 해결함

합성곱 신경망의 구성 요소

합성곱 층 (convolutional layer)
활성화 함수 (activation function)
풀링 층 (pooling layer)
완전 연결 층 (fully connected layer)
정규화 (normalization)
드롭아웃 (dropout)

합성곱 층

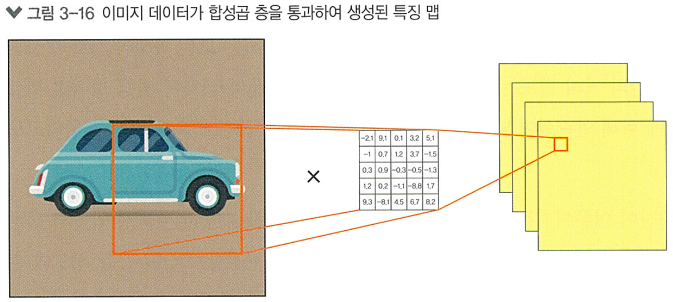
합성곱 층에 존재하는 사각형의 가중치 필터를 합성곱 필터라 하며, 입력된 이미지 데이터와 연산됨

필터
> 합성곱 층에서 입력 데이터의 특징을 추출하기 위해 연산되는 가중치들의 집합
> 형태가 이미지 데이터와 동일한 3차원 행렬 (6면체)
> 이미지의 좌측 상단부터 우측 하단까지 오른쪽으로 한 칸씩 이동

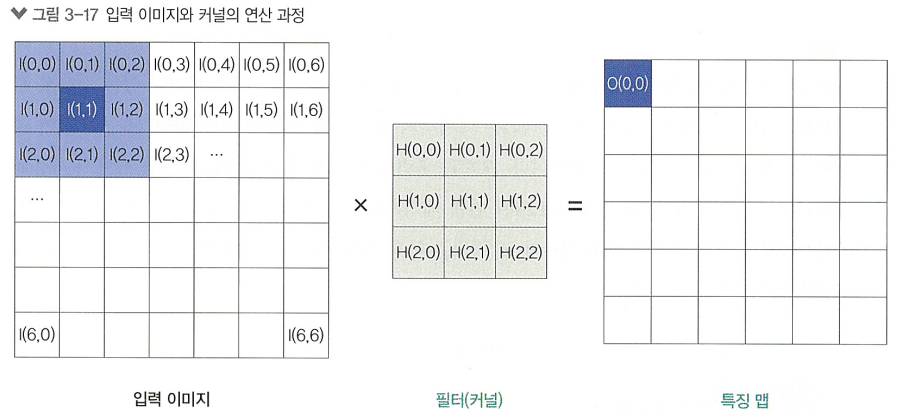
좌측 상단 픽셀들과 합성곱 필터의 연산 결과는 특징 맵의 좌측 상단에,
우측 하단 픽셀들과 합성곱 필터의 연산 결과는 특징 맵의 우측 하단에 위치함
>> 공간 정보를 유지하여 특징 맵에 전달!

커널
> 종종 혼용되지만, 커널 $\not=$ 필터
> 커널은 이미지의 특정 패턴이나 특징을 감지하는데 사용되는 2차원 행렬 (사각형)임
> 필터는 여러 개의 커널로 이루어짐!
> 커널은 합성곱 필터 내에 포함되어 있고, 필터는 채널 축을 따라 이동하지 않는다
필터는 입력 데이터와 항상 같은 채널을 가지기 때문!

채널
> 입력 행렬의 채널 수와 출력 행렬의 채널 수는 관련이 없음!
오히려 출력 행렬의 채널 수 == 사용된 필터 수

ex) 채널 수가 128인 입력 데이터에 합성곱 필터를 1개만 사용하면,
생성되는 특징 맵의 채널 수는 1개

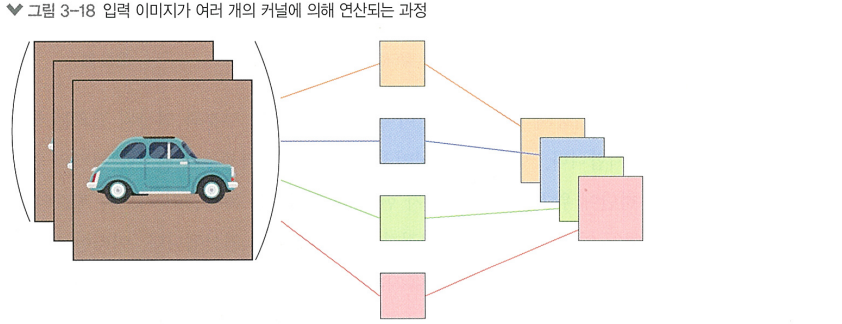
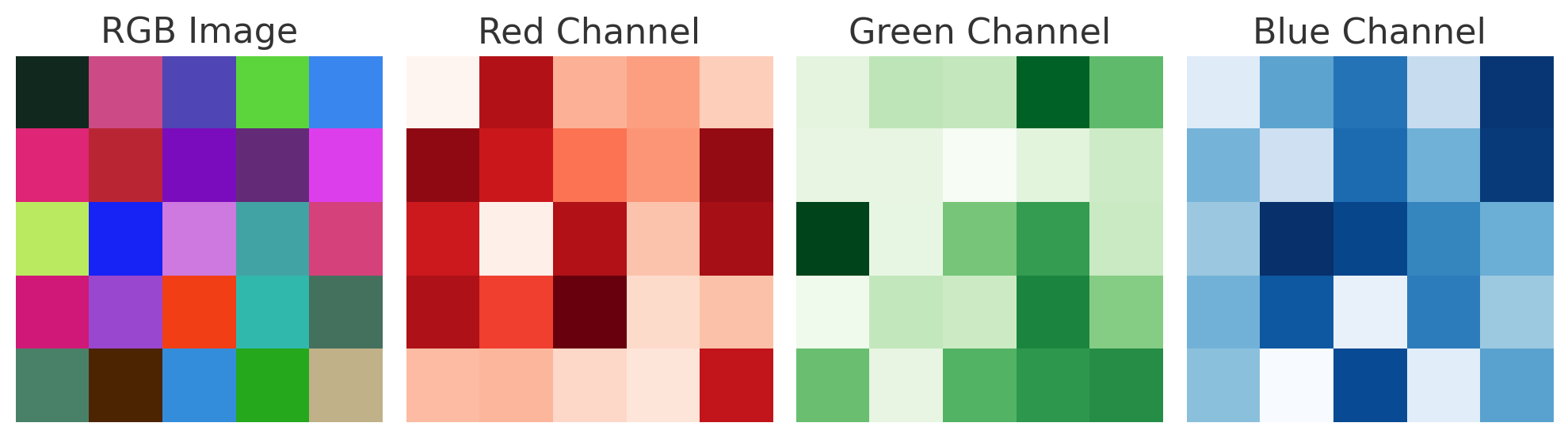
RGB 이미지는 R,G,B 3개의 채널을 가짐

패딩
> 입력 데이터 주변에 특정값(pad)을 추가하는 과정, 주로 0으로 이루어진 테두리 사용
> 패딩 없이 합성곱 연산을 수행하면 출력의 사이즈는 입력보다 작아지기 때문에 사용됨
합성곱 층을 여러번 거쳐 사이즈가 줄어들면 점점 정보가 손실됨
> 이미지의 모서리 픽셀은 필터가 단 한번만 거쳐 연산이 끝나는 반면,
가운데 픽셀은 몇번씩 거쳐 연산에 참여함
>> 패딩은 이런 정보의 손실을 방지하고, 모든 부분이 누락되지 않고 연산에 참여하게끔 함

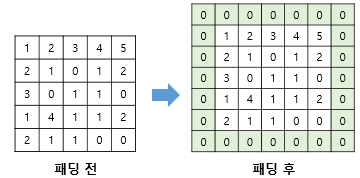
"""패딩 표현 방법"""
from tensorflow.keras.layers import Conv2D

conv_layer = Conv2D(fliters=32, kernel_size=(3,3), activation='relu', padding='same')
# padding 인수 값을 same으로 지정하면 상황에 맞는 사이즈로 입력 데이터에 패딩이 더해짐
# padding 인수 값을 valid로 지정하면 패딩을 적용하지 않음
# 패딩없이 (3,3) 커널이라면 가로 세로 2픽셀 씩 줄어서 출력됨 (스트라이드가 1일때)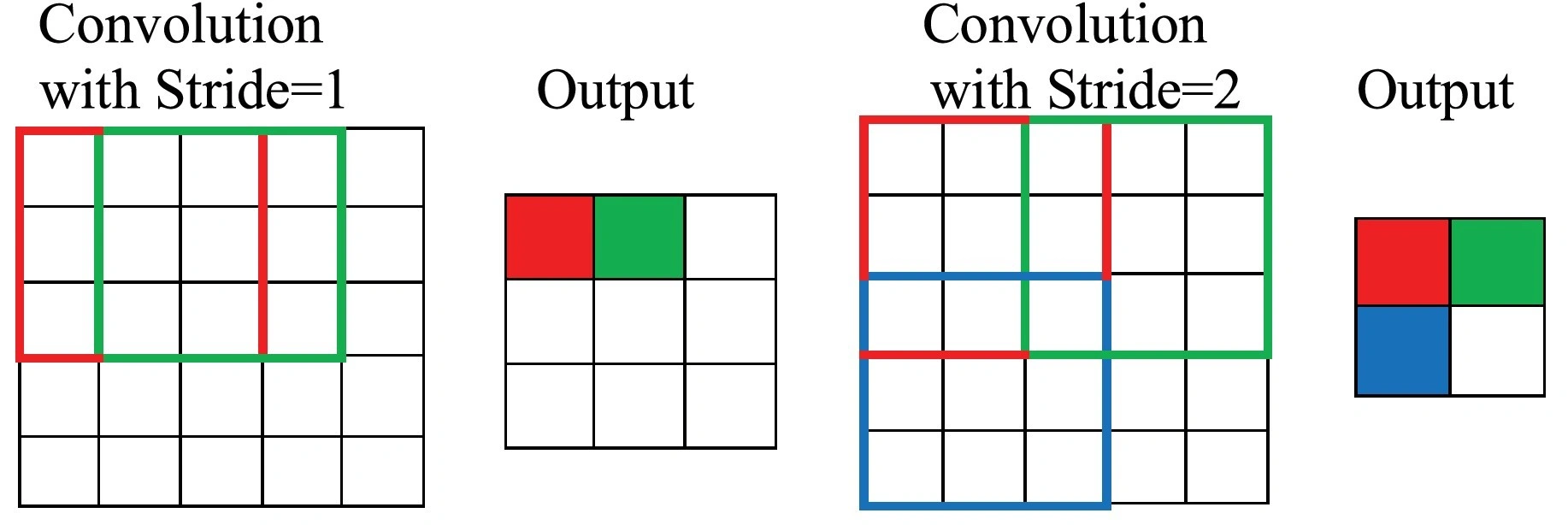

스트라이드
> "합성곱 필터가 연산을 한 번 수행한 후 움직이는 거리"
> 스트라이드가 작으면 윈도우가 이동 횟수가 증가하고, 크면 윈도우의 이동 횟수가 감소함
> 스트라이드를 크게 설정하면 연산이 줄어들지만, 특징을 놓칠 수 있다는 단점이 있음
특징 맵이 작아져 합성곱 층을 깊게 쌓기 어려워진다는 단점도 있음

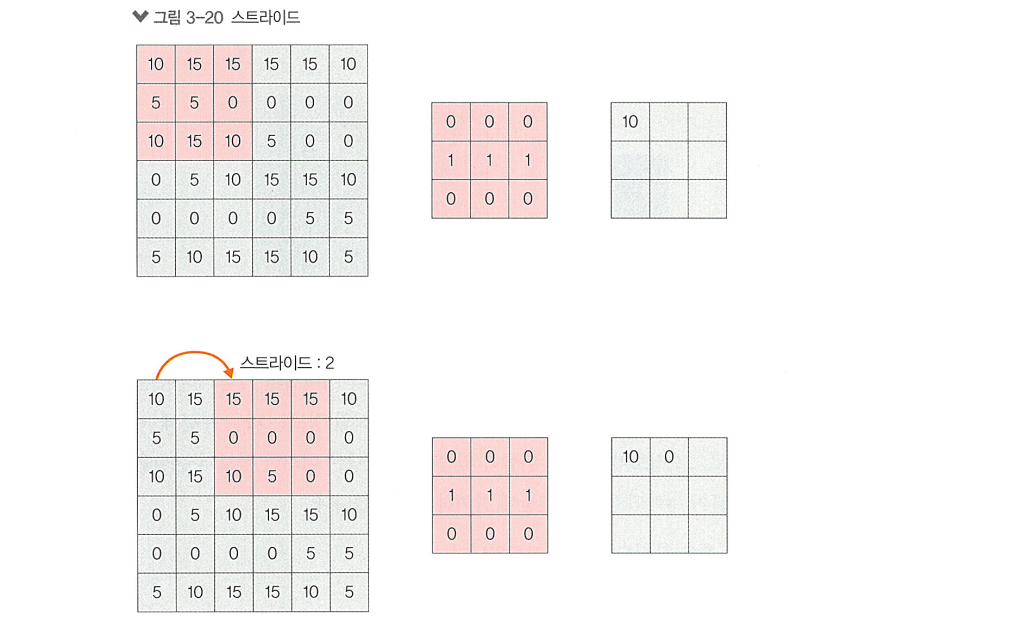
"""스트라이드 표현 방법"""
from tensorflow.keras.layers import Conv2D

# 방법 1
conv_layer = Conv2D(fliters=32, kernel_size=(3,3), activation='relu', padding='same', stride=(1,1))

# 방법 2
conv_layer = Conv2D(fliters=32, kernel_size=(3,3), activation='relu', padding='same', stride=1)

# 위의 두 가지 방식으로 표현 가능

합성곱 연산 과정

(224, 224, 3) 형태의 이미지가 아래와 같은 두 단계의 합성곱 층을 거치며 어떤 과정을 겪는지 알아보자

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D

input_shape = (224, 224, 3)

model = Sequential()

model.add(Conv2D(32, kernel_size=(3,3), strides=(1,1), padding='same', activation='relu', input_shape=input_shape))
model.add(Conv2D(64, kernel_size=(5,5), strides=(2,2), padding='valid', activation='relu'))

첫번째 합성곱 층: 3x3 사이즈의 필터가 32개 존재, 스트라이드 1, 패딩 적용 O
두번째 합성곱 층: 5x5 사이즈의 필터가 64개 존재, 스트라이드 2, 패딩 적용 X

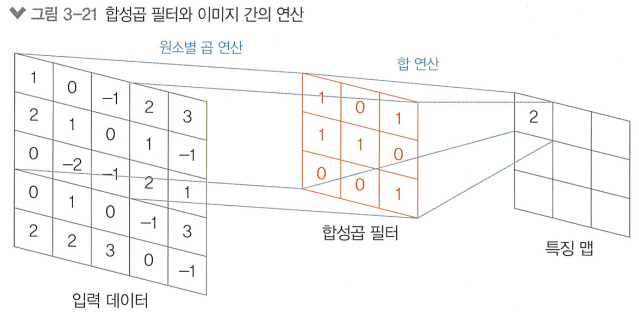
첫번째 합성곱 층의 필터 사이즈 = (3,3,3) (=입력과 동일한 채널 수)
하나의 윈도우를 연산할때,
(각각의 픽셀과 곱해진 합성곱 필터 내부 값) x (필터 채널 수) = 9x3 = 27
총 27개의 값이 전부 합쳐져 하나의 값으로 표현

이런 과정을 거쳐 좌측상단부터 우측하단까지 연산을 끝마치면, 패딩을 적용했기에 사이즈가 줄지않은
(224, 224, 1) 형태의 출력 데이터를 갖게되는데, 필터의 개수를 32개로 설정했으므로
(224, 224, 32) 형태의 특징 맵이 만들어짐

두번째 합성곱 층의 필터 사이즈 = (5,5,32) (=입력과 동일한 채널 수)
스트라이드가 2이기 때문에,
좌측의 첫번째 픽셀에서 연산을 시작해 두 칸씩 이동하면
한 줄의 마지막 픽셀에서 연산이 깔끔하게 나눠떨어지지 않음
>> 해당 픽셀은 연산 불가능으로 인식하고 그냥 아래로 이동함

위와 같은 특징을 반영해 합성곱 층을 통과하며 출력 데이터 사이즈가 어떻게 변하는지 식으로 표현됨

\text {output size} = \frac {\text{input size} - \text{filter size}}{\text{stride}} + 1

*주의 - 합성곱 연산 과정 중 패딩 등의 다른 연산은 적용하지 않고
필터 사이즈와 스트라이드 값만을 조정한 결과만 반영하고,
식의 결과 값이 정수가 아닐 경우 소숫점은 버려야함

\frac{224 - 5}{2} + 1 = 110.5 \;\; \rarr \;\; 110

패딩을 적용 안 했기에 (110, 110, 1) 형태의 출력 데이터를 갖게되는데, 필터의 개수를 64개로 설정했으므로
최종적으로 (110, 110, 64) 형태의 특징맵이 만들어짐

+) 전치 합성곱
합성곱 필터의 연산 방식을 수정한 방식, 특징 맵의 사이즈를 확장하는데 이용됨

+) 확장 합성곱
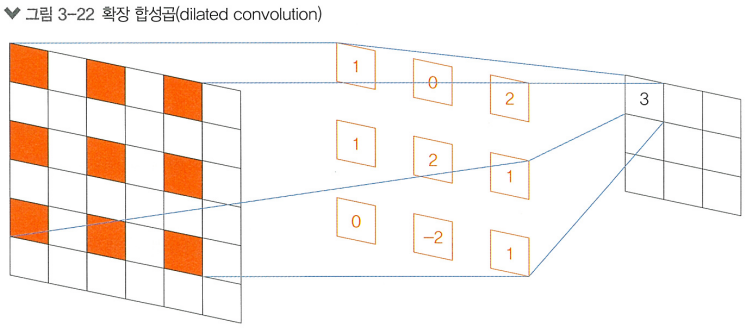
합성곱 필터의 연산 방식을 수정한 방식, 일정한 간격만큼 떨어진 픽셀과 연산을 수행함

풀링

일반적인 CNN은 합성곱 층을 여러번 배치해서 입력된 데이터의 채널의 사이즈는 늘리되,
가로와 세로 사이즈를 줄여가며 학습을 수행함
> 합성곱 층만 사용해서 사이즈를 줄이는건 비효율적!
> 풀링 층을 함께 사용해야함!!
> 풀링 층은 합성곱 층의 뒤에 붙여 특징 맵을 입력으로 받고, 풀링 연산을 수행한 결과를 출력

특징 맵의 사이즈를 줄이는 데 사용되는 기법.
합성곱 층보다 적고 빠른 연산, 적은 메모리 사용
객체가 약간 이동해도 결과가 안 달라지도록 모델의 강건함에 도움줌

커널 윈도우와 유사하게 동작하여 윈도우 사이즈, 스트라이드, 패딩 등의 인수를 통해 제어 가능

"""합성곱층+풀링층 적용 예시"""
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, Maxpooling2D

input_shape = (224, 224, 3)

model = Sequential()

model.add(Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=input_shape))
model.add(MaxPooling2D(pool_size=(2, 2)))  # 풀링 윈도우 사이즈 = 2x2

model.add(Conv2D(64, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))  # 풀링 윈도우 사이즈 = 2x2

최대풀링이 가장 많이 사용되고, 평균 풀링, 최소 풀링, 전역 풀링(특징 맵의 전역에서 대표값 추출) 등이 있음

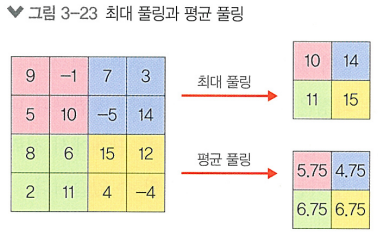
위는 스트라이드를 2로 설정하고 각각 최대 풀링, 평균 풀링 했을때의 결과이다.

>> 여러 층으로 쌓인 합성곱 층과 풀링 층으로 정보를 축약하고 더 넓은 범위의 맥락을 이해

3.1.3 생성적 적대 신경망(GAN)

이미지 생성

생성하는 모델은 데이터에서 자주 등장하는 패턴을 학습하고,
이를 일반화시켜 재구성하여 결과물을 '그럴듯'하게 만들어냄

이미지 생성 모델에 필요한 요소
> 우선, 이미지에서 특징을 추출하는 능력이 필요함

정밀하고 모호하지않은 이미지를 출력해야한다.
이미지를 사실적으로 묘사할 수 있어야한다.
이미지의 품질을 (수치 상으로) 평가하는 능력도 필요하다.

이미지 생성과 비지도 학습

지도학습
> 각각의 데이터에 레이블이 제공되어, 모델이 연산한 결과와 레이블을 비교하며 학습함
> 라벨링 하는데에 큰 비용과 노동력이 요구됨
> 라벨링 하는데에 논리적 근거가 충분치 않아 데이터를 못 만드는 경우도 있음
이미지 생성을 위한 데이터세트의 레이블은 인간의 주관이 관여되기 때문

위와 같이 데이터를 만들기 어려운 경우,

비지도 학습을 통해 모델을 학습시킬 수 있음
> 레이블 없이 데이터 자체의 특성만을 기반으로 학습함
ex) 군집화, 차원 축소, 연관 규칙 학습 등

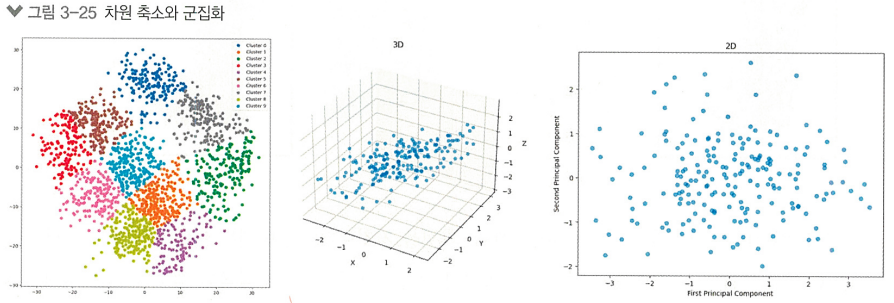
>> 레이블을 전혀 활용하지 못하기에 지도학습보단 학습효율이 떨어짐.
>> GAN에선 비지도 학습을 하되, 간이 레이블을 만들어 우회적 지도 학습 방식을 사용함

오토 인코더

> GAN 이 생기기 전, GAN에 많은 영감을 제시한 대표적 이미지 생성 기법

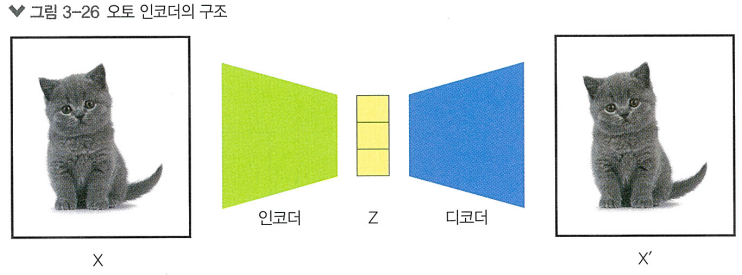
오토 인코더는 두개의 과정을 거침.

1단계
> 이미지의 표현을 파악하고, 이 정보를 작은 사이즈로 압축하는 과정 = 인코딩

2단계
> 압축된 정보를 원본 이미지의 사이즈와 비슷하게 재구성 하는 과정 = 디코딩

$z = f(x)$
인코더 $(f)$ 에서는 입력 데이터 $(x)$ 를 $x$ 보다 작고 밀도 높은 표현인 잠재공간 $(z)$ 으로 매핑함

$x' = g(z)$
디코더 $(g)$ 에서는 인코더에서 생상한 잠재공간 $z$ 를 다시 원래의 데이터 $x'$ 로 복원하는 과정을 거침

$x \approx x'$
재생성된 이미지 $(x')$ 가 원본 이미지 $(x)$ 와 차이나지 않도록 모델을 학습시키는 것이 목표

>> 오토 인코더는 비지도 학습을 한다는 것을 알 수 있음!

인코더
> 비지도 학습 중 차원 축소와 비슷한 역할을 수행함
> 여러 층을 진행시키며 차원을 축소하고, 중요하고 의미 있는 정보를 탐색함
> 비선형 특성까지 고려할 수 있음 (PCA는 선형 관계에만 효과적)

디코더
> 축소된 잠재 공간을 원래의 데이터 공간으로 복원하는 역할
> 즉, 원본 이미지와 같은 사이즈로 유사한 이미지를 생성해내도록 학습

오토 인코더의 다양한 응용과 한계

응용
> 특징 추출기, 이미지 복원

한계
> 원하는 형태의 이미지를 생성하기 위해선 이에 상응하는 이미지를 입력으로 주어야함 (제한적임)
> 구조가 단순해서 생성하는 표현이 제한됨 (입력 이외의 표현 묘사 불가능)

GAN의 아이디어

> 정답이 없는 상태에서도 정답이 있는 것처럼 학습할 수 있음 (비지도 학습)
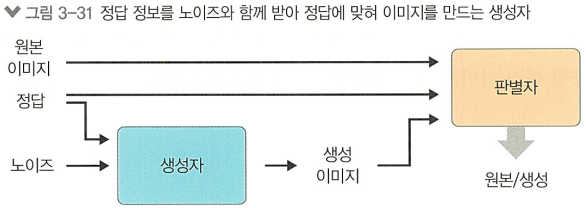
> 실제 데이터와 유사한 생성 데이터를 만드는 '생성자(Generator)',
> 생성된 데이터가 원본인지 판별하는 '판별자(Discriminator)'가 서로 경쟁하는 구조

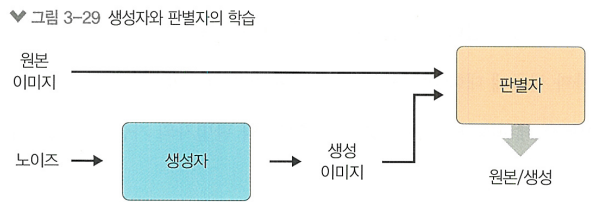
판별자가 가짜 데이터를 진짜라고 구별하게될 확률을 최소화하려고 노력하는 동안,
생성자는 그 확률을 최대화하려고 노력함
>> 진행되면서 양측이 정교하게 학습되며, 결국 높은 품질의 생성 데이터를 만들게됨

생성자
> 생성한 데이터로 판별자를 속여 가짜 데이터를 실제 데이터로 분류하게끔 만드는 것이 목적
> 랜덤노이즈/잠재공간에서 샘플링된 벡터를 입력으로 받아,
생성자 신경망을 통과하며 최종적으로 실제 데이터와 동일한 형태를 가진 데이터를 출력함

판별자
> 입력으로 주어진 샘플이 실제 데이터인지, 생성자가 만든 가짜 샘플인지 구별하는 것이 목적
> 이진 분류 문제를 해결하는 모델 (진짜=1, 가짜=0)
> 이진 교차 엔트로피 손실 함수를 사용해, 실제 레이블과 판별자의 출력 사이 오차를 최소화함

[판별자 학습 과정]
  1. 생성자로 가짜 샘플 만듬
  2. 실제 데이터 샘플과 가짜 샘플을 각각 입력받아 판별자가 출력하는 확률 갑 계산
  3. 진짜 샘플에 대한 손실, 가짜 샘플에 대한 손실. 둘을 합해 총 손실을 계산
  4. 총 손실에 대한 그레디언트를 계산하고, 이를 사용해 생성자와 판별자의 가중치 업데이트

>> GAN이 훈련이 진행될수록 판별자의 정확도는 개선되며,
이는 생성자에게 더 높은 질의 샘플을 생성하도록 요구함

GAN의 학습 실습

"""mnist데이터 로드"""
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, Flatten, Reshape
from tensorflow.keras.models import Sequential
from tensorflow.keras.datasets import mnist
from tqdm import tqdm
from google.colab.patches import cv2_imshow

(train_images, _), (_, _) = mnist.load_data()
train_images = (train_images - 127.5) / 127.5

cv2_imshow(train_images[0]*127.5+127.5)  # 이미지 하나 출력

모델 생성

"""생성자 모델 함수"""
def build_generator(input_dim):
    model = Sequential()
    model.add(Dense(512, input_dim=input_dim, activation='relu'))
    model.add(Dense(28*28, activation='tanh'))
    model.add(Reshape((28, 28)))
    return model

"""판별자 모델 함수"""
def build_discriminator():
    model = Sequential()
    model.add(Flatten(input_shape=(28, 28)))
    model.add(Dense(256, activation='relu'))
    model.add(Dense(1, activation='sigmoid'))
    return model

"""하이퍼파라미터 정의"""
INPUT_DIM = 50  	# 랜덤 노이즈의 차원 수
BATCH_SIZE = 64		# 미니 배치의 사이즈
EPOCHS = 10			# 전체 데이터를 총 학습할 횟수
BUFFER_SIZE = 600	# 데이터 세트를 섞어줄 단위

"""생성자/판별자 모델 선언"""
generator = build_generator(INPUT_DIM)
discriminator = build_discriminator()

"""최적화 기법 선언"""
generator_optimizer = tf.keras.optimizers.Adam(1e-3)
discriminator_optimizer = tf.keras.optimizers.Adam(1e-2)

"""학습데이터를 tf.data.Dataset으로 변환"""
train_dataset = tf.data.Dataset.from_tensor_slices(train_images)\
                  .shuffle(BUFFER_SIZE).batch(BATCH_SIZE)

손실 함수 정의
> 생성자와 판별자의 손실 함수를 따로 정의해서 각각의 학습 목적을 정의함
> 판별자는 원본과 생성본을 잘 구분하는지를, 생성자는 판별자를 잘 속였는지를 기준으로 정의

binary_cross_entropy = tf.keras.losses.BinaryCrossentropy()
"""
real_output: 원본 이미지를 보고 판별자가 판단한 결과 값. (1이 정답)
fake_output: 생성 이미지를 보고 판별자가 판단한 결과 값. (0이 정답) """
def discriminator_loss(real_output, fake_output): 
    real_loss = binary_cross_entropy(tf.ones_like(real_output), real_output)
    fake_loss = binary_cross_entropy(tf.zeros_like(fake_output), fake_output)
    total_loss = real_loss + fake_loss
    return total_loss

""" fake_output이 얼마나 1과 가까운지로 손실을 판별 """
def generator_loss(fake_output):
    return binary_cross_entropy(tf.ones_like(fake_output), fake_output)

"""학습하는 함수"""

@tf.function

# 단 한번의 가중치 업데이트를 위한 함수
def train_step(images):
    noise = tf.random.normal([BATCH_SIZE, INPUT_DIM])
	
    # 연산을 기록하고, 이를 사용해 손실 함수로부터 그레디언트 계산
    with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
      generated_images = generator(noise, training=True)

      real_output = discriminator(images, training=True)
      fake_output = discriminator(generated_images, training=True)

      gen_loss = generator_loss(fake_output)					# 생성자 손실 계산
      disc_loss = discriminator_loss(real_output, fake_output)	# 판별자 손실 계산

    gradients_of_generator = gen_tape.gradient(gen_loss, generator.trainable_variables)				# 생성자 그레디언트 계산
    gradients_of_discriminator = disc_tape.gradient(disc_loss, discriminator.trainable_variables)	# 판별자 그레디언트 계산

    generator_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))				# 생성자 가중치 업데이트
    discriminator_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables))	# 판별자 가중치 업데이트
    
    return gen_loss, disc_loss, generated_images

모델 학습

for epoch in range(1,EPOCHS+1):
    t = tqdm(train_dataset)
    for image_batch in t:
        g_loss, d_loss, fake_image = train_step(image_batch)
        t.set_description_str(f"Epoch - {epoch}")
        t.set_postfix({"G_loss":"%0.3f" %g_loss.numpy(),
                       "D_loss":"%0.3f" %d_loss.numpy()})
    cv2_imshow(np.concatenate(
        list(fake_image.numpy()[:10]*127.5+127.5),axis=1))