프롤로그

leetCode의 Maximum-Product-Subarray와 Maximum-Subarray를 풀던 도중에 카데인 알고리즘에 대한 내용이 나와서 이 글을 정리하게 되었습니다.

우선 카데인 알고리즘을 이해하기전에, 다이나믹 프로그래밍에 대한 개념을 짧게 설명해보겠습니다.
그 후 Maximum-Subarray 문제를 브루드 포스로 접근한 후 카데인 알고리즘을 사용해 개선해나가는 방식으로 풀이해보겠습니다.

다이나믹 프로그래밍

다이나믹 프로그래밍은 복합한 문제를 단순한 서브(하위) 문제들의 모음으로 나누고 각각의 서브 문제를 한 번만 해결한 다음 메모리 기반 데이터 구조(리스트, 맵 등)를 사용하여 해결책을 저장함으로써 해결하는 방법입니다. 다음에 같은 서브 문제가 나타나면 다시 계산하는 대신에 단지 이전에 계산된 문제를 확인함으로써 시간을 줄이는 것입니다.

블로그에 다이나믹 프로그밍을 설명하는 재밌는 예시가 있어서 가져왔습니다.

4살짜리 아이에게 다이나믹 프로그래밍을 어떻게 설명할까요?

종이에 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 를 적은 후, 아이에게 답을 묻는다.
아이 : (숫자를 센 후) 8!
문제의 왼쪽에 1 + 을 추가한 후, 아이에게 다시 답을 묻는다.
아이 : (빠르게) 9!
어떻게 그렇게 빠르게 9라고 알았어? 라고 물으니 아이는 "단지 1을 더했어요!"라고 답한다.
답이 8이였다는 것을 기억하기 때문에 단지 그 값에 1을 더했을 뿐, 1부터 9까지 다시 셀 필요가 없다! 다이나믹 프로그래밍은 이처럼 그저 "시간을 절약하기 위해 무언가를 기억하는 것" 입니다.

이보다 다이나믹 프로그래밍은 복잡하지만, 이 글은 카데인 알고리즘을 알아보기 위한 글이기에 여기서 넘어가겠습니다. 만약 다이나믹 프로그래밍에 대해서 더 자세히 알고싶다면 링크를 클릭해주세요.

Maximum Subarray Problem

maximum subarray problem은 가장 큰 연속적인 서브 배열의 합을 구하는 문제입니다.

A = [-2, 1, -3, 4, -1, 2, 1, -5, 4]

예를 들어 위의 배열에서 가장 큰 합을 가지는 연속적인 서브 배열은 [4, -1, 2, 1](합 6) 입니다. 이제 아래에서 이 배열을 가지고 브루드 포스와 카데인 알고리즘으로 접근해서 문제를 풀이해보겠습니다.

브루드 포스 접근

좋은 방법은 아니지만 가장 명백한 풀이는 모든 서브 배열의 합을 계산한 후 거기서 최댓값을 찾는 것입니다. 아래의 그림과 같이 인덱스 0부터 시작해서 A[0]로 시작하는 모든 서브 배열의 합을 계산합니다. 그 후 인덱스를 증가해 A[1], A[2], ... , A[n-1]에서 시작하는 모든 서브 배열의 합을 차례대로 구해나갑니다.

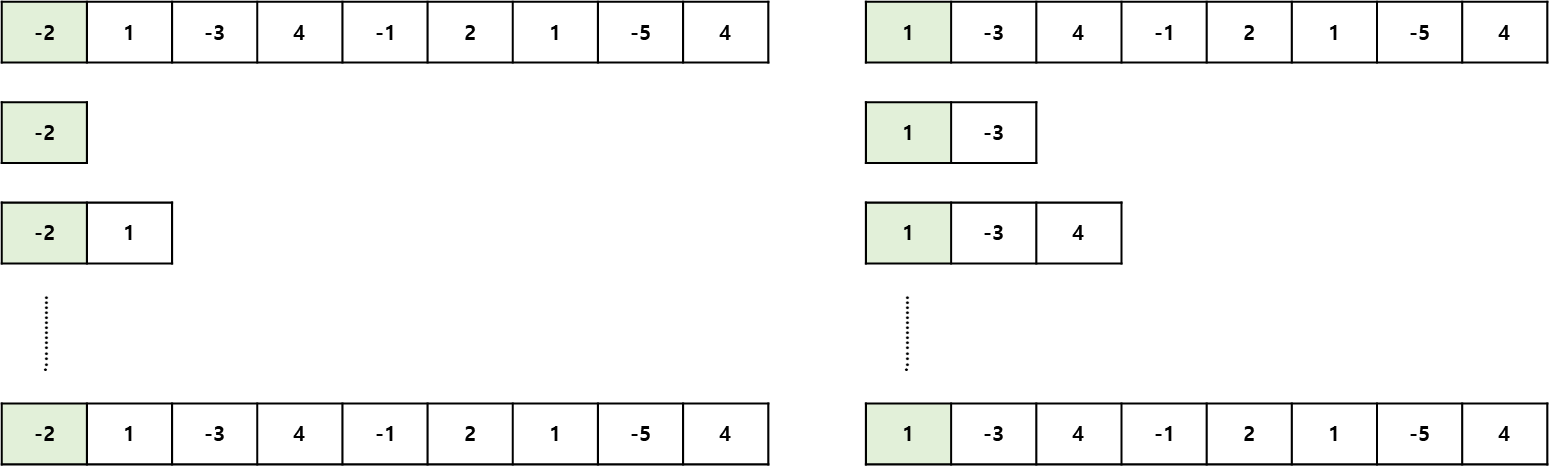
브루도 포스로 접근하여 문제를 풀이한다면 과정은 아래와 같습니다.

1. 배열 A의 인덱스 0번부터 시작해서, A[0]번의 서브 배열의 모든 부분 합을 구합니다.
2. A[0]의 가능한 모든 부분합 중에서 가장 큰 부분합을 local_maximum0 라고 부릅니다.
3. 1,2의 방식을 A[1], A[2], ... A[n-1]까지 반복합니다.
4. 인덱스 0부터 N-1까지 각 인덱스에 해당하는 local_maximum0 ~ local_maximumN-1이 구해집니다.
5. 구해진 local_maximum들 중에서 가장 큰 값을 찾습니다. 이 값이 global_maximum으로 최종적으로 가장 큰 부분합이 됩니다.

다만 이러한 방식은 배열이 커진다면 복잡도가 급격하게 올라갑니다. 시간 복잡도는 배열의 크기가 n이라고 한다면 O(n^2)으로 좋은 풀이 방법이 아닙니다. 이제 이것을 다이나믹 프로그래밍으로 풀이해서 접근해보겠습니다.

카데인 알고리즘

이제 카데인 알고리즘으로 접근하는 방법을 알아보겠습니다. 우선 카데인 알고리즘을 증명하기 위해서, 브루드 포스와 같은 방식으로 접근하지만 뒤에서부터(A[n-1]) 접근하는 방식으로 바꿔보겠습니다. 이때, A[4] (= -1)과 A[5] (= 2)로 끝나는 서브 배열을 확인해보겠습니다.

위의 그림을 자세히 보면 A[5]까지의 서브 배열을 구할 때 A[4]까지의 서브 배열의 값이 사용된다는 것을 알 수 있습니다. 즉 아래의 그림과 같은 규칙을 확인할 수 있습니다.

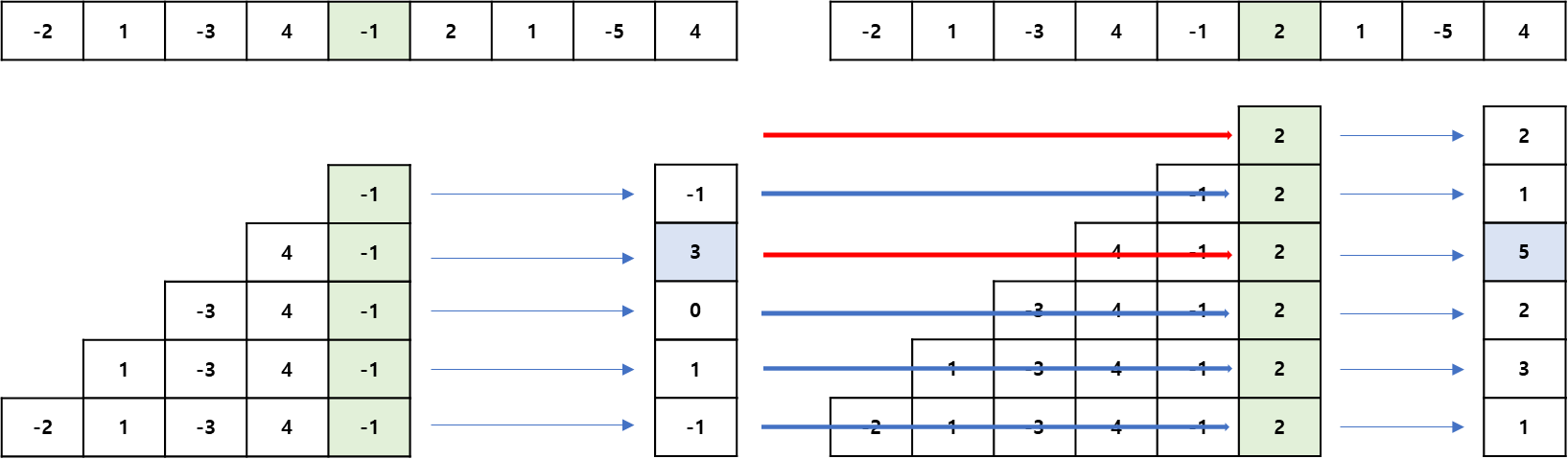
이제 위의 규칙을 확인할 수 있게 그림에 화살표를 추가했습니다. A[5](= 2)의 값을 구하는 표를 보면 서브 배열이 두 개의 파트로 나누어지는 것을 확인할 수 있습니다. A[4](= -1)까지의 서브 배열 값(화살표에 해당하는 부분)과 A[5] 자기 자신만을 포함하는 서브 배열이 있습니다.

이와 같은 규칙을 최댓값을 찾는데 적용해보면 우선 저희는 local_maximum4(A[4]까지의 서브 배열 중 최댓값)를 알고 있습니다. 그림에서 왼쪽의 파란색으로 칠한 3에 해당합니다.
따라서 local_maximum5(A[5]까지의 서브 배열 중 최댓값)를 구하는데 A[4]로 끝나는 서브 배열의 결과를 알고 있기에, A[5]로 끝나는 모든 서브 배열을 확인할 필요가 없습니다. 단지 그림에서 빨간색 화살표로 표시한 부분만 계산하면 됩니다. 이는A[4]서브 배열 중 최댓값 + A[5] 또는 A[5]에 해당합니다.

즉, 정리하자면 인덱스 i에 해당하는 A[i]까지의 서브 배열의 최댓값은 이전 서브 배열의 최댓값 + 자기 자신 또는 자기 자신 중 최댓값에 해당하는 것입니다. 이를 식으로 표현하면 아래와 같습니다.

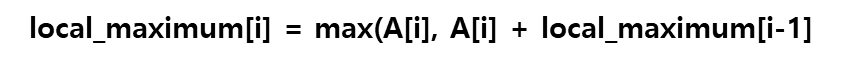
이러한 방식으로 모든 인덱스 i에서 문제는 A[i] 또는 (A[i] + local_maximum[i-1]) 두 개의 숫자중에서 최댓값을 찾는 문제로 바뀌게 됩니다. 참고로, local_maximum0의 값은 A[0] 자기 자신입니다.

위에서 설명했듯이, 브루드 포스에 비해서 카데인 알고리즘의 연산의 횟수는 굉장히 줄어듭니다. 따라서 카데인 알고리즘의 시간 복잡도는 O(n)에 해당합니다. 이제 파이썬으로 코드를 작성해보겠습니다.

코드

# 카데인 알고리즘으로 접근
def maxSubArray(nums: List[int]) -> int:
    local_max = 0
    global_max = -sys.maxsize

    for num in nums:
        # 이전의 최댓값 + 자기 자신 or 자기 자신중 최댓 값 구하기
        local_max = max(num, local_max + num)
        # 최종 결과 갱신
        global_max = max(global_max, local_max)

    return global_max

참조
Kadane's Algorithm - How and Why does it Work?
Dynamic Programming - Kadane's Algorithm(카데인 알고리즘)
How should I explain dynamic programming to a 4-year-old?