이코테 시리즈

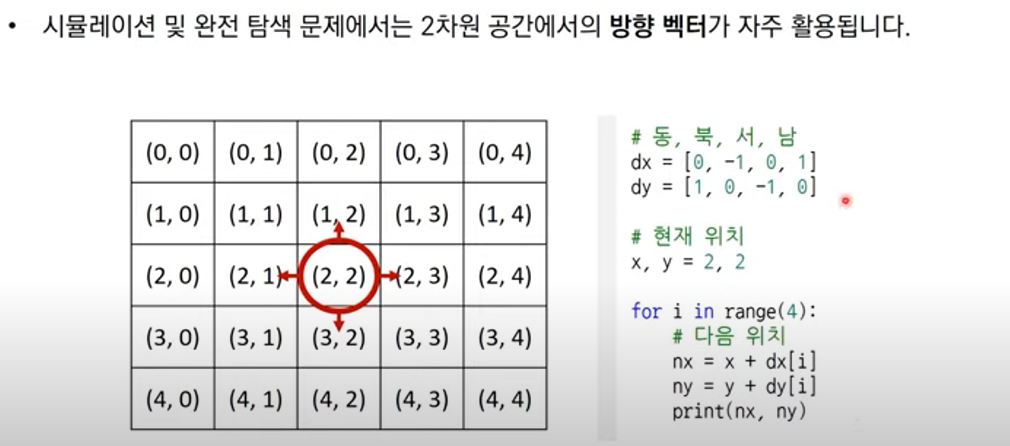
단순히 가장 좋아 보이는 것을 반복적으로 선택해도 최적의 해를 구할 수 있는지 검토한다.탐욕법으로 얻은 해가 최적의 해가 되는 상황에서, 이를 추론할 수 있어야 한다.ex) 거스름 돈 문제가 그리디 알고리즘으로 풀 수 있다는 정당성을 가지는 케이스는 가지고 있는 동전

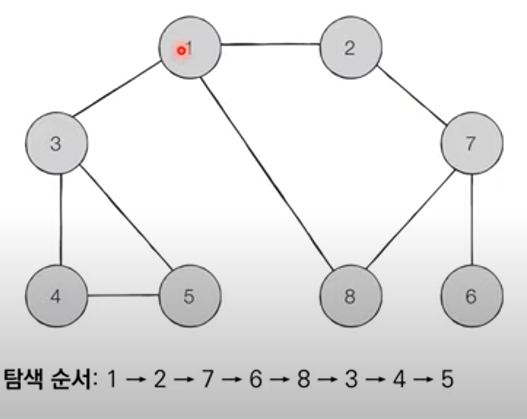
둘다 그래프 자료구조의 전체 노드를 방문할 수 있는 탐색 알고리즘이다.1\. 깊이 우선 탐색으로 노드를 스택에 삽입하고 방문 처리를 한다.2\. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문처리한다. 방문하지 않은 인접

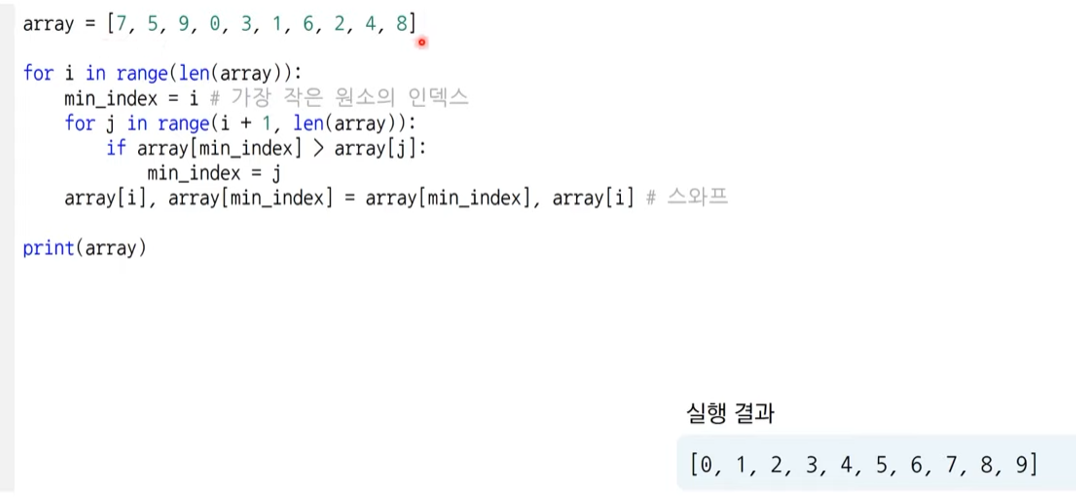
처리되지 않은 데이터 중에서 가장 작은 데이터를 '선택'하여 맨 앞에 있는 데이터와 바꾸는 것을 반복한다.매번 데이터 중에서 가장 작은 값을 골라야 하기 때문에 이중 반복문을 사용해서 구현한다. O(n\*\*2)처리되지 않은 데이터를 하나씩 골라 적절한 위치에 삽입하는

정렬되어 있는 리스트에서 탐색 범위를 좁혀가며 데이터를 탐색하는 방법.시작점과, 끝점, 중간점을 이용하여 탐색 범위를 설정한다.정렬이 되어있는 리스트에서 작동하기 때문에 탐색전 정렬이 필요하다코테에서는 보통 데이터의 개수가 1000만개를 넘어가거나 탐색 범위의 크기가

메모리를 적절히 사용하여 수행 시간 효율성을 향상시키는 방법이미 계산된 결과는 별도의 메모리에 저장하여 다시 계산하지 않도록 한다.구현은 탑다운, 바텀업으로 구성된다.동적할당과 상관없음 그냥 의미 없음다음과 같은 문제일 때 사용1\. 최적 부분 구조큰 문제를 작은 문제

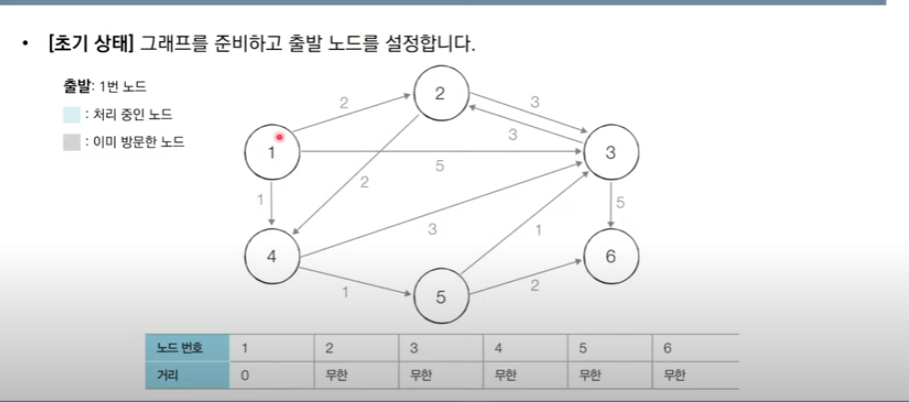
다익스트라 알고리즘은 음의 간선이 없을 때 정상적으로 작동한다. (현실 세계의 도로)또한 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정을 반복하기 때문에 그리디 알고리즘으로 분류된다.출발 노드를 설정최단 거리 테이블을 초기화방문하지 않은 노드 중에서 최단 거

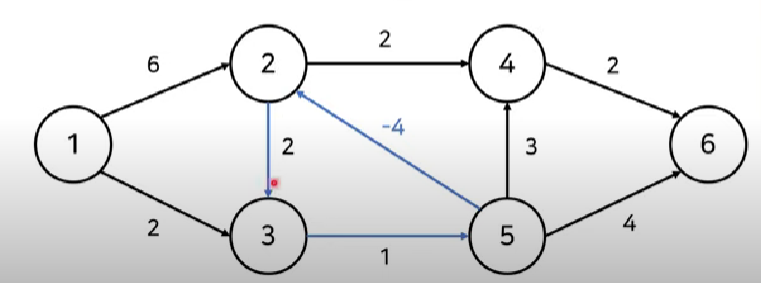
출발 노드에서 다른 모든 노드로 가는 최단 경로를 구하는 다익스트라 알고리즘은 출발 노드로 부터 특정 노드를 거쳐서 다른 노드들로 갈 때 최소값을 매번 힙으로 찾는다.만약 특정 경로를 통해 비용이 줄어들 수 있다면 다익스트라 알고리즘은 그 경로를 거쳐서 최단 경로 테이

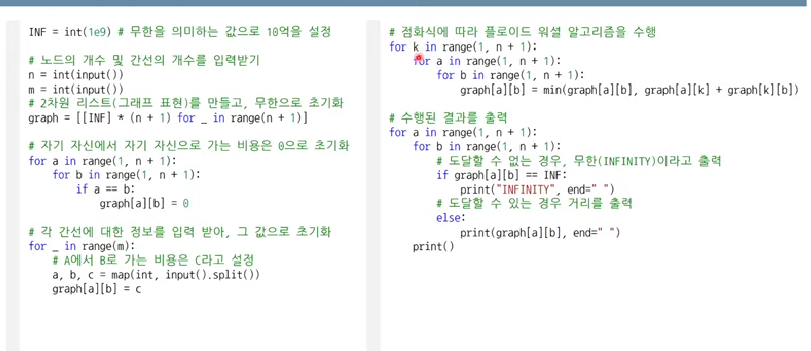
다익스트라 알고리즘은 출발 노드에서 다른 노드까지 가는 최단 경로를 특정 노드를 통해 거쳐가는 값을 계산하여 구했다면(제일 적은 비용을 가진 간선만 방문) 플로이드 와샬 알고리즘은 모든 노드에서 모든 노드에 거쳐서 다른 모든 노드로 갈 수 있는 경우의 수를 계산하여 모