최단 경로 - 벨만포드

출발 노드에서 다른 모든 노드로 가는 최단 경로를 구하는 다익스트라 알고리즘은 출발 노드로 부터 특정 노드를 거쳐서 다른 노드들로 갈 때 최소값을 매번 힙으로 찾는다.
만약 특정 경로를 통해 비용이 줄어들 수 있다면 다익스트라 알고리즘은 그 경로를 거쳐서 최단 경로 테이블의 모든 값을 음의 무한대 값으로 만들 것이다.

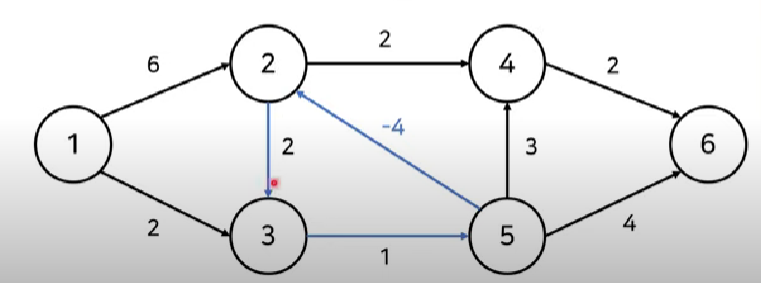
벨만 포드 알고리즘은 출발 노드에서 특정 노드를 통해 다른 노드로 가는 값을 구할 때 모든 간선에 대해 비용을 계산한다. 만약 최소 값이 나온다면 테이블을 갱신한다. 이렇게 했을 때 특정 노드에서 시작했을 때 다른 모든 노드로 가는 거리 경우의 수를 간선의 갯수 만큼 계산하고 비교한다는 것이다. O(VE)

n개의 노드가 있을 때 위와 같은 작업을 n-1번 수행하면 n번째는 해볼 필요도 없이 최단 거리 테이블이 갱신되었을 것이다. 만약 n번째 수행했을 때 최단 거리 테이블이 갱신된다면 특정 경로를 거쳤을 때 테이블의 특정 값이음수로 줄어들었다는 것이므로 위 사진처럼 음수 순환 경로가 존재한다는 것이므로 테이블 값을 구할 수 없다.

https://velog.io/@kimdukbae/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%B2%A8%EB%A7%8C-%ED%8F%AC%EB%93%9C-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Bellman-Ford-Algorithm

def bf(start):
    # 시작 노드에 대해서 초기화
    distance[start] = 0
    # 전체 v - 1번의 라운드(round)를 반복
    for i in range(v):
        # 매 반복마다 '모든 간선'을 확인한다.
        for j in range(e):
            cur_node = edges[j][0]
            next_node = edges[j][1]
            edge_cost = edges[j][2]
            # 현재 간선을 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
            if distance[cur_node] != INF and distance[next_node] > distance[cur_node] + edge_cost:
                distance[next_node] = distance[cur_node] + edge_cost
                # v번째 라운드에서도 값이 갱신된다면 음수 순환이 존재
                if i == v - 1:
                    return True

    return False


# 벨만 포드 알고리즘 수행
negative_cycle = bellman_ford(1)

# 음수 순환이 존재하면 -1 출력
if negative_cycle:
    print("-1")
else:
    # 1번 노드를 제외한 다른 모든 노드로 가기 위한 최단 거리를 출력
    for i in range(2, v + 1):
        # 도달할 수 없는 경우, -1 출력
        if distance[i] == INF:
            print("-1")
        # 도달할 수 있으면 거리 출력
        else:
            print(distance[i])