최단 경로 - 다익스트라 알고리즘

다익스트라 알고리즘

다익스트라 알고리즘은 음의 간선이 없을 때 정상적으로 작동한다. (현실 세계의 도로)
또한 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정을 반복하기 때문에 그리디 알고리즘으로 분류된다.

1. 출발 노드를 설정
2. 최단 거리 테이블을 초기화
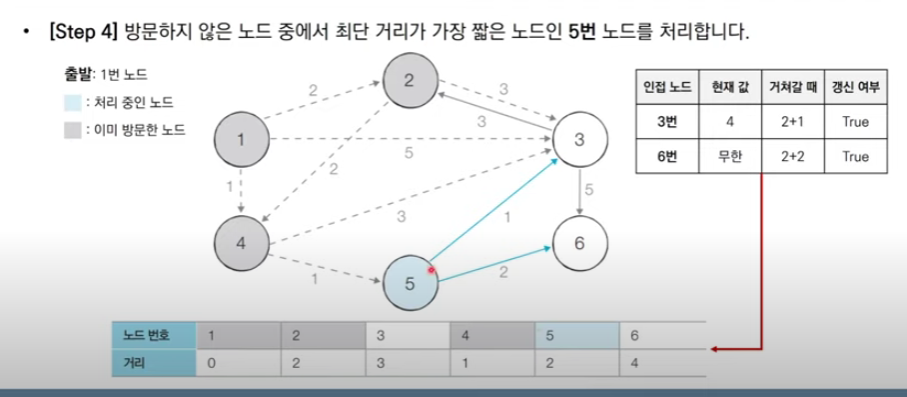
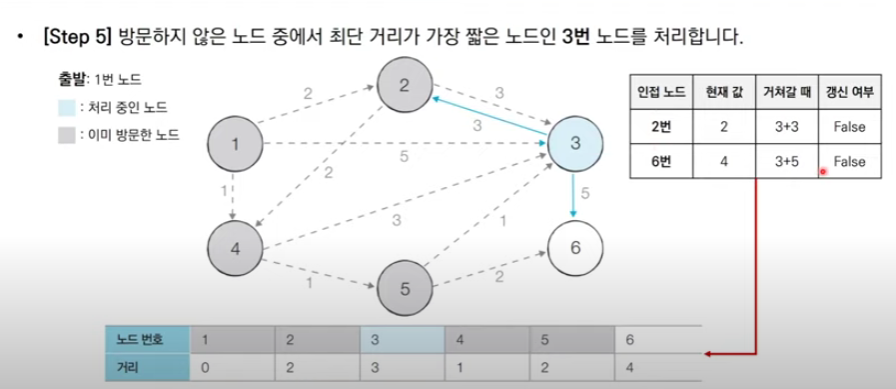
3. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신
5. 3, 4번 반복

그림으로 알아보면,

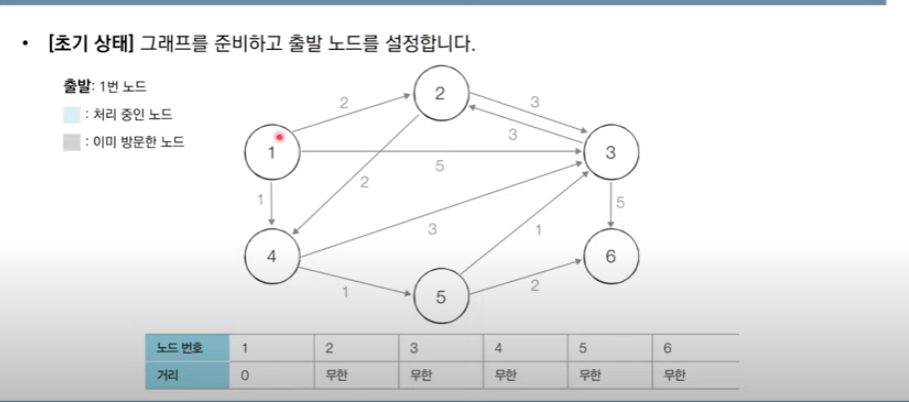
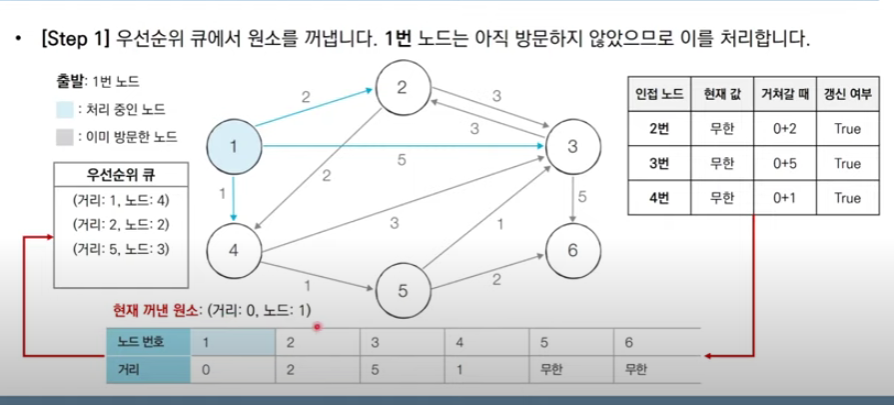
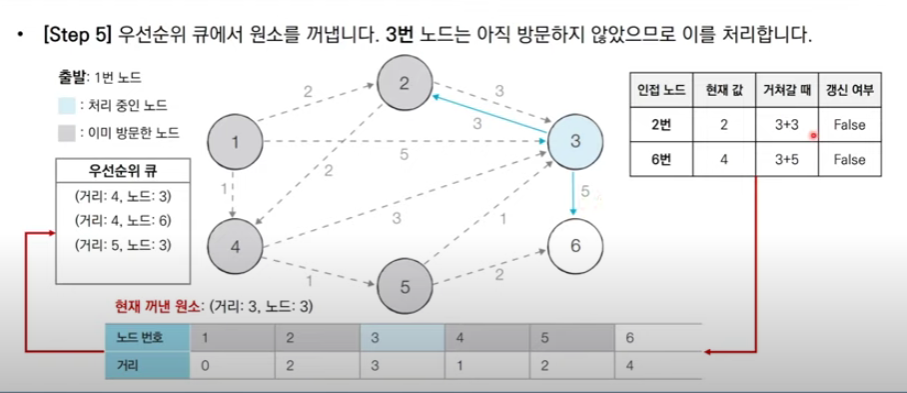
먼저 출발 노드를 설정한다.(1)

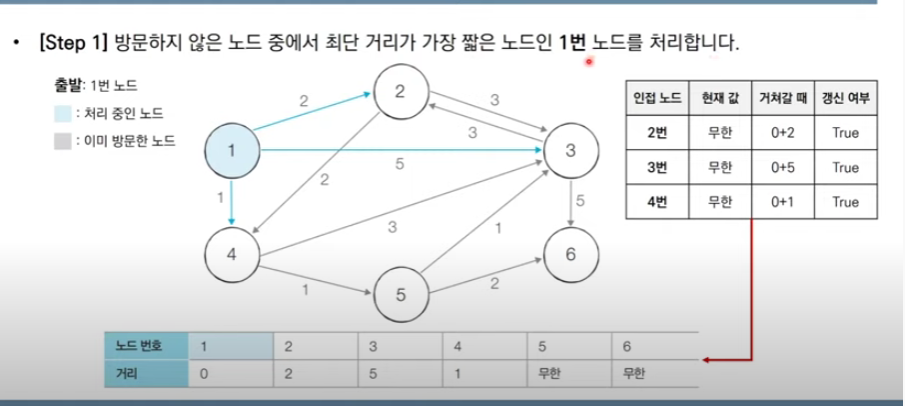
1번 노드에서 1번 노드까지는 0이라고 치고 방문 처리한다.

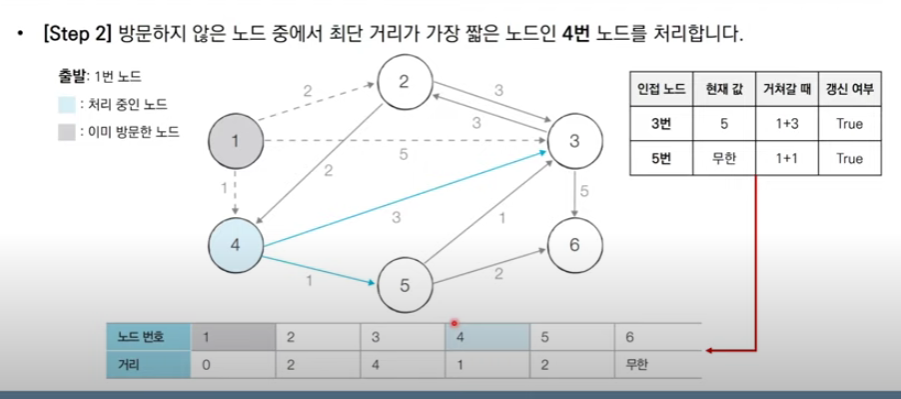
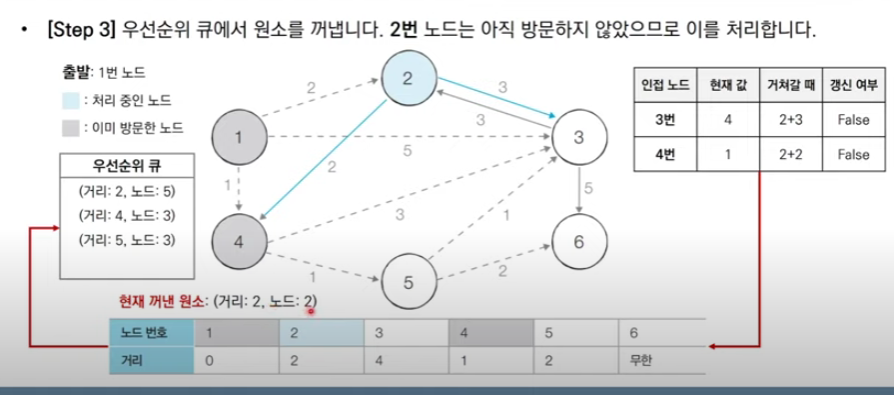
최단 거리 테이블 중에서 방문하지 않은 노드 중 1번 노드까지의 가장 짧은 4번 노드를 방문하여 처리한다. 또한 4번을 거쳐 다른 노드로 갈 때 그 노드에서 1번 노드까지의 거리가 더 짧으면 그 노드의 값을 1->4->node값으로 테이블을 갱신한다.

방문을 한다는 의미는 이미 그 노드에서 1번 노드까지의 거리가 최단이라는 것이고 방문하고 나서는 1번 노드에서 그 노드를 거쳐 다른 노드로 가는 거리를 계산하여 다른 노드의 최단 거리 테이블을 갱신한다는 것에 의미가 있다.

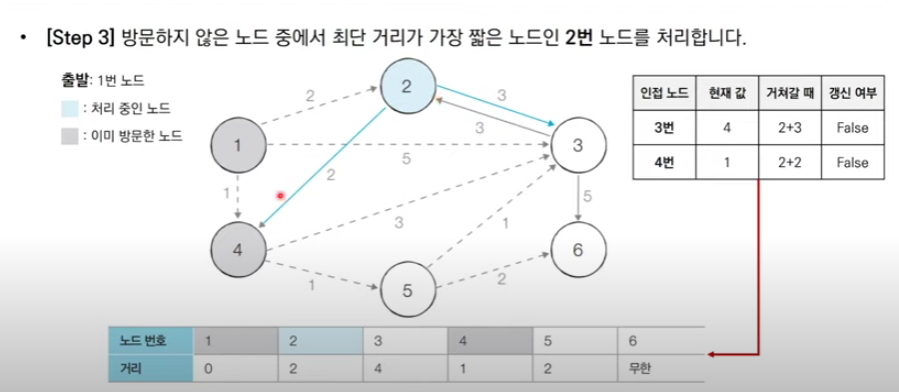
다시 최단 거리 테이블에서 가장 짧은 2번 노드를 방문하여 처리하고 (2,5의 값이 같지만 번호가 적은 노드부터 방문)

반복

가장 짧은 노드를 매번 선형 탐색하므로 시간 복잡도는 O(n**2)이다. 하지만 방문할 노드를 찾는 작업을 우선순위 큐(최소 힙) 자료구조를 써서 최단 거리가 가장 짧은 노드를 자동으로 pop 한다면 O(ElogN)으로 복잡도를 줄일 수 있다.

import heapq
import sys
input = sys.stdin.readline
INF = int(1e9) #무한을 의미하는 값으로 10억 설정

#노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
#시작 노드 번호를 입력받기
start = int(input())
#각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[]for i in range(n+1)]
#최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n+1)

#모든 간선 정보 입력받기
for _ in range(n):
	a, b, c = map(int, input().split())
    # a번 노드에서 b번 노드로 가는 비용이 c라는 의미
    graph.append((b,c))
    
def dijkstra(start):
	q = []
    # 시작 노드로 가기 위한 최단 거리는 0으로 설정하여, 큐에 삽입
    heapq.heappush(q, (0, start))
    distace[start] = 0
    while q: #큐가 비어있지 않다면
    	#가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
        dist, now = heapq.heappop(q)
        #현재 노드가 이미 처리된 적이 있는 노드라면 무시
        if distance[now] < dist: #현재 방문할 큐의 dist가 해당 노드의 최단거리 테이블에 있는 거리보다 짧으면 이미 처리되었단 뜻이므로
        	continue
       	for i in graph[now]:
        	cost = dist + i[1]
            # 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
          	if cost < distance[i[0]]:
            	distance[i[0]] = cost
                heapq.heappush(q, (cost, i[0]))
                
# 다익스트라 알고리즘 수행
dijkstra(start)

#모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n+1):
	# 도달할 수 없는 경우, 무한(infinity)이라고 출력
    if distance[i] == INF:
    	print("INFINITY")
    # 도달할 수 있는 경우 거리를 출력
    else:
    	print(distance[i])

파이썬의 heapq라이브러리는 힙 자체가 최소힙으로 기본 설정 되어있어서 그냥 쓰면됨