Convolution

• convolution의 시작은 signal processing에서 두 개의 함수를 섞어주기 위한 operator

• Continuous convolution

  $(f*g)(t) = \int f(\gamma)g(t-\gamma)d\gamma = \int f(t-\gamma)g(\gamma)d\gamma$

• Discrete convolution

  $(f*g)(t) = \sum_{i=-\infty}^\infty f(i)g(t-i) = \sum_{i=-\infty}^\infty f(t-i)g(i)$

• 2D image convolution

  $(I*K)(i,j) = \underset{m}{\sum}\underset{n}{\sum} I(m,n)K(i-m,j-n) = \underset{m}{\sum}\underset{n}{\sum} I(i-m,j-n)K(m,n)$

  • $I$ : 전체 이미지, $K$ : Convolution Filter

2D image에서, Stride, padding을 고려하지 않고 가장 기본적인 convolution을 하면 연산은 다음과 같다.
kernel과 image에서 겹친 부분을 성분곱을 취한 후 합쳐서 특정 feature map이 생성된다. 이 과정은 kernel(K, filter)이 image(I) 위를 한칸씩 움직이며 접하는 모든 부분에서 시행하여, 7x7 image에 대해 3x3 kernel(filter)를 convolution하면 5x5의 feature map이 출력된다.

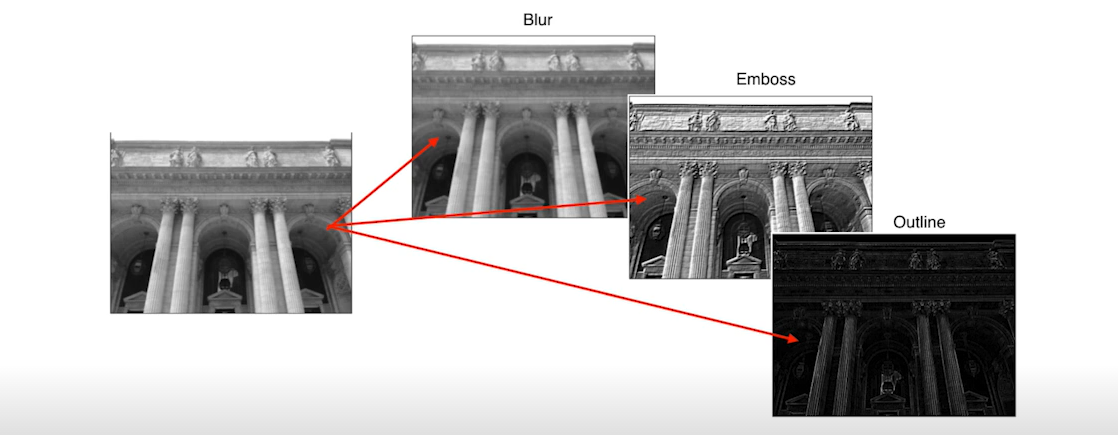
여기서 kernel(filter)의 모양에 따라 출력 이미지에 blur, emboss, outline 등의 효과가 발생한다.

RGB Convolution

일반적으로 다루는 image는 RGB 이미지로 tensor로 표현하면 32 x 32 x 3 image로 RGB의 3개 채널(dimension)에 대해 depth로 표시된다.
따라서, 예로 5x5 filter를 사용한다고 하더라도 depth 3을 생략하고 언급한 것이기에 이 부분을 꼭 놓치지 말아야 한다.

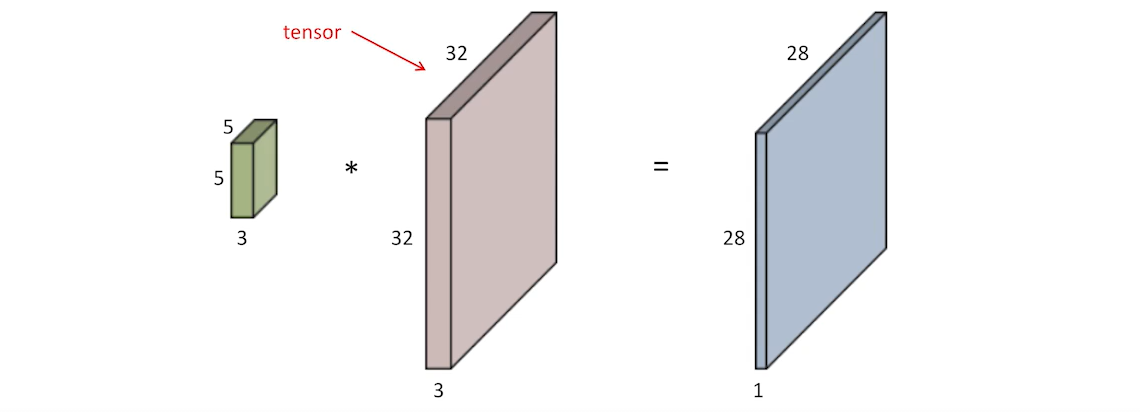
32x32x3 RGB image에서도 5x5(x3) filter를 적용하면 output은 ch이 1인 feature map이 생성된다. 만약 이러한 5x5 filter가 n개 있다고 한다면, output의 ch 개수도 n개가 된다. 따라서, input ch과 output ch을 알면 filter의 크기도 알 수 있다.

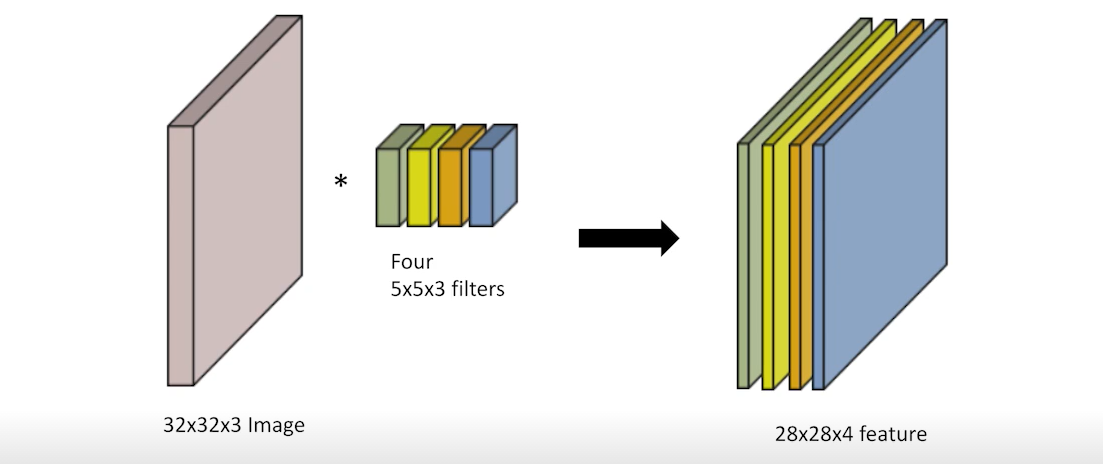
Stack of Convolutions

만약 여러 개의 Convolution으로 모델을 생성한 경우 어떤 식으로 연산 과정이 진행될까?

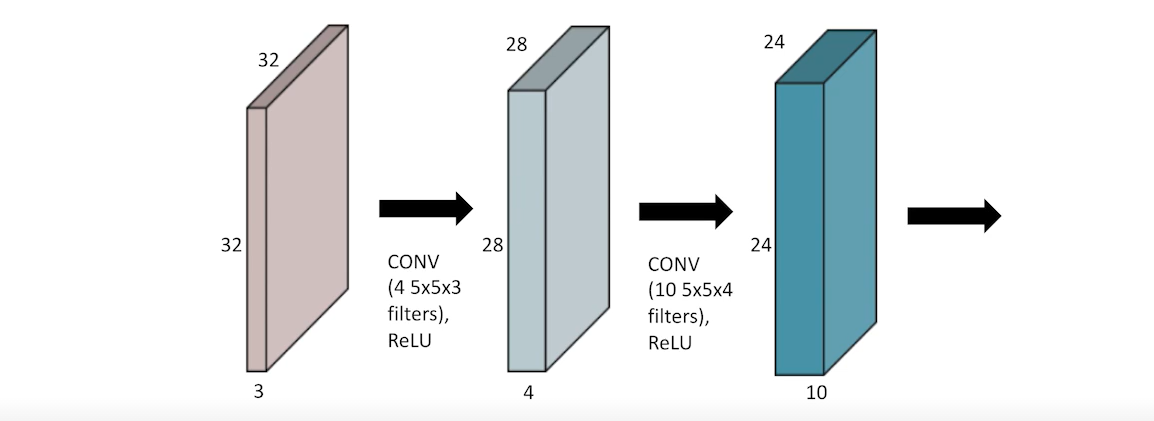
그림과 같이, 우선 32x32x3 image가 크기가 4인 5x5x3 filter 및 비선형 함수를 거쳐서 28x28x4 feature map이 생성된다. 이후 동일한 과정을 통해 24x24x10의 feature map이 생성된다.

여기서 parameter 수는 kernel size x input ch 개수 x output ch 개수로, 첫번째 conv를 보면, 5x5x3x4가 parameter 개수가 된다.

CNN(Convolution Neural Networks)

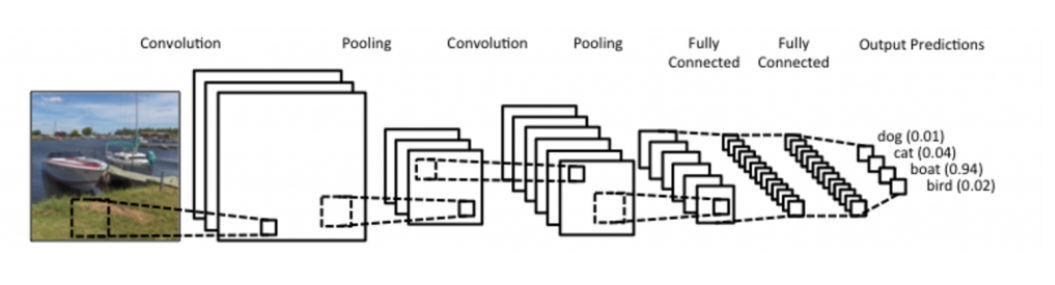
이러한 일련의 과정들을 합쳐서, CNN은 convolution layer, pooling layer, and filly connected layer로 구성되어 있다.

convolution & pooling layers : featture extraction
Fully connected layer : decision making(e.g., classification)

아래 과정은 일반적인 CNN의 과정으로, 최근엔 뒷단의 fully connected layer가 줄어드는 추세이다. 그 이유는 모델 학습 시 parameter 개수가 많을수록 학습이 어렵고 generalization performance가 저하된다(이 부분은 CNN 뿐만 아니라 SVM, Tree model 등도 다 포함된다). 따라서 CNN의 발전 방향은, 같은 model을 만들고 최대한 convolution layer를 깊게 쌓는 동시에 파라미터 숫자를 줄이는데에 다양한 방법론이 있다.

Convolution Arithmetic

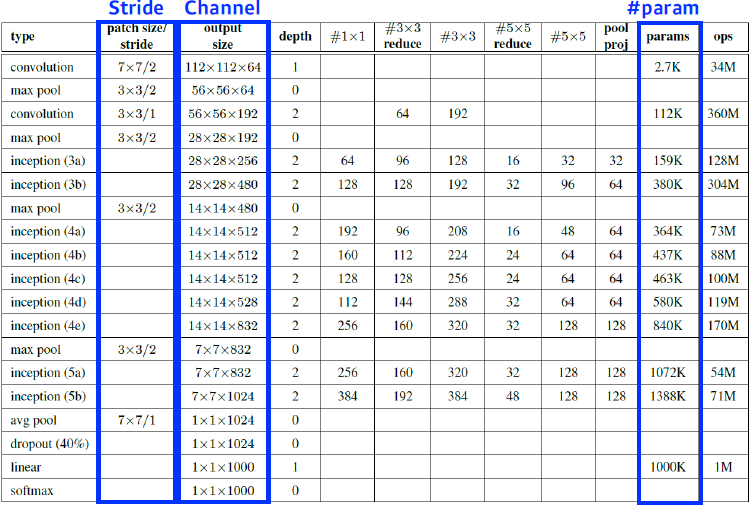
아래 표는 GoogleNet의 layer별 parameter를 계산한 결과이다.

Stride

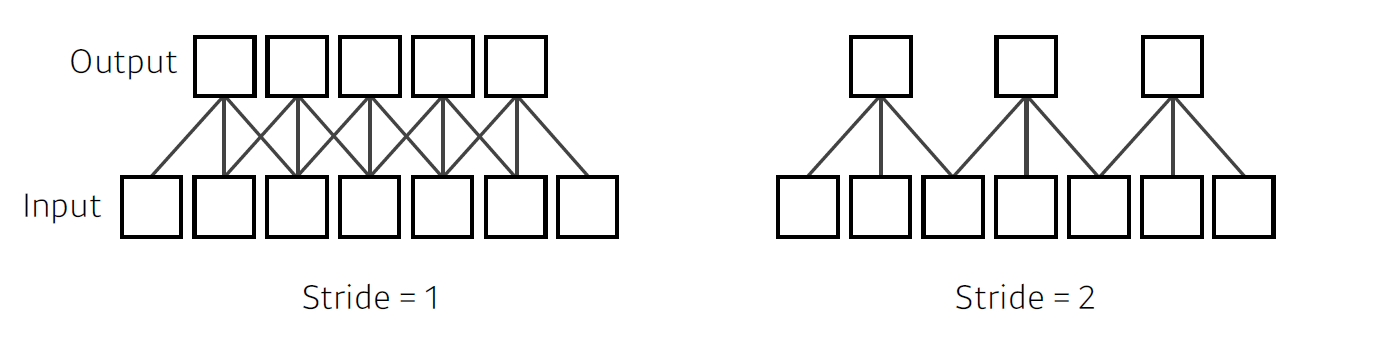
Stride는 Kernel의 step size로, stride=1이면 한칸씩 움직이며, stride=n이면 n칸씩 filter가 움직인다.

Padding

32 x 32인 image에 convolution operation을 수행하면 output feature map 다른 size로 출력이 된다. 그 이유로는, filter가 image의 가장자리를 찍을 수 없기 때문인데, 만약 적절한 크기의 Padding을 통해 가장자리를 채워줄 수 있으면 가장자리 역시 convolution operation을 수행할 수 있으며, 출력은 기존과 같은 32 x 32의 feature map을 가질수 있다.

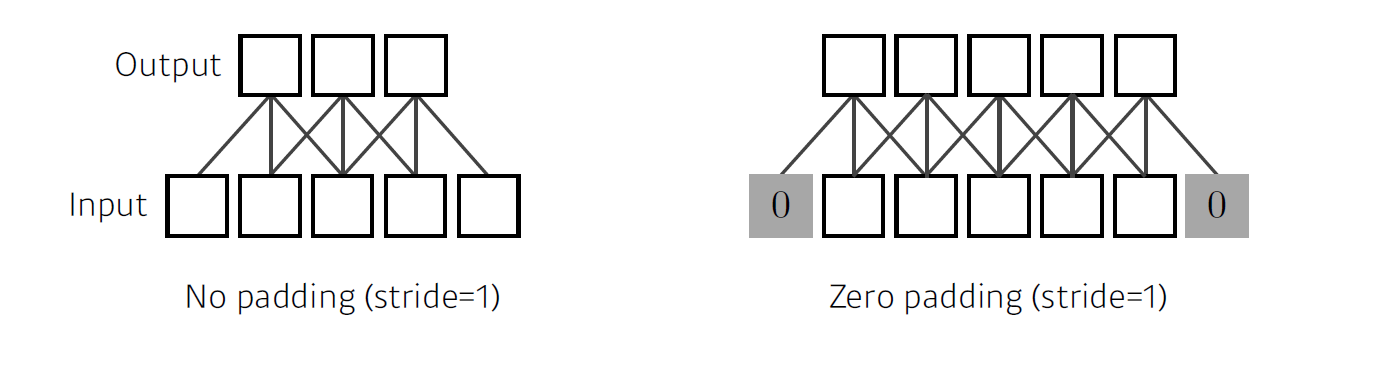
결과적으로 padding과 stride를 적절히 조절하면 feature map의 size를 조절할 수 있다.

Convolution Arithmetic

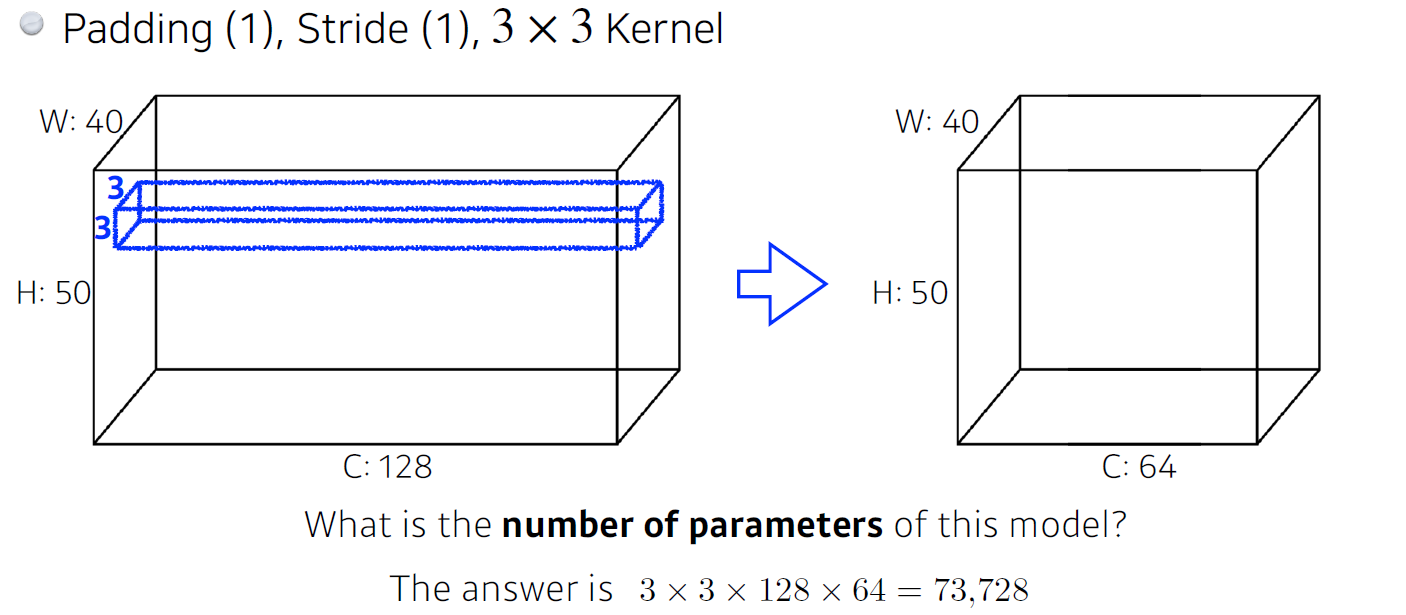
아래와 같이 convolution layer가 있을 때, 파라미터의 개수는 몇개일까?

input이 40x50x128이고 output이 40x50x50이며, filter map이 3x3이므로, parameters=$73,728$개(3x3x128(input dimension 크기, kernel 채널 크기)x64(output dimension 크기, 커널의 개수))개가 된다.

padding과 stride는 parameter 개수에 영향을 주지 않다.

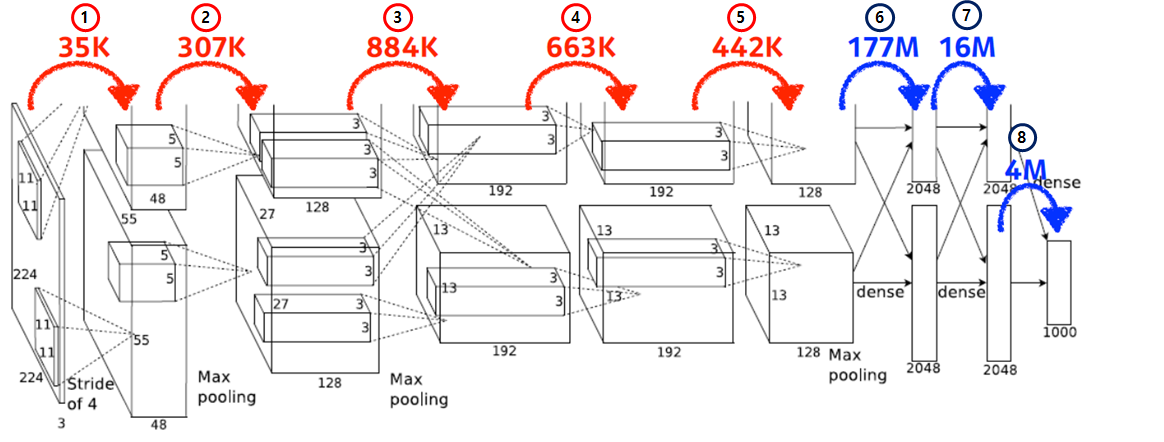
해당 내용을 바탕으로 아래 모델(AlexNet)의 parameter 개수를 계산해보자. 몇개일까?

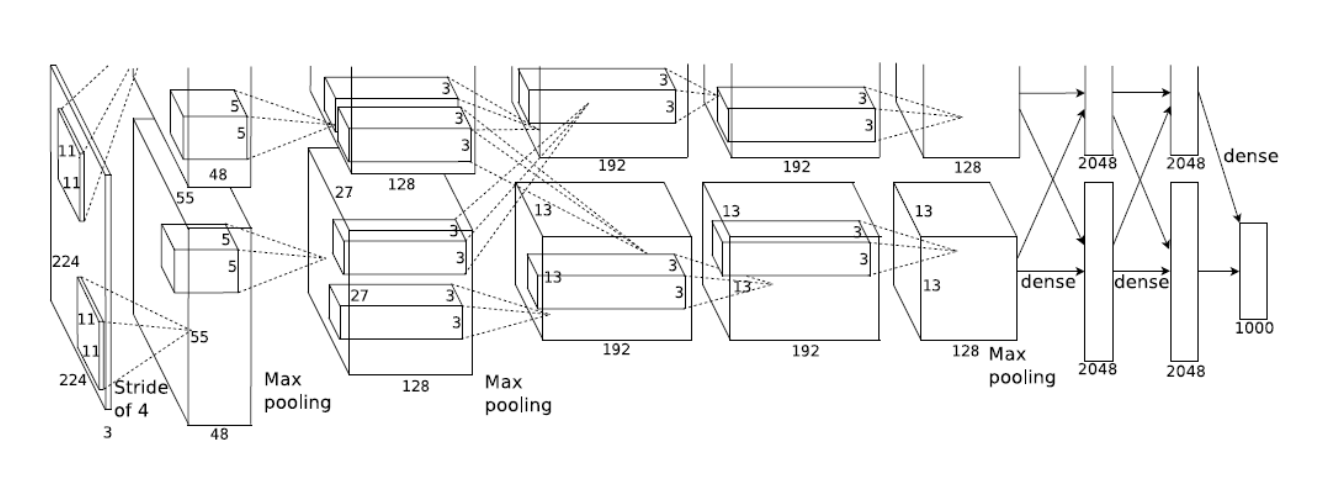
첫 번째 층을 보면, input feature map은 224 x 224 x 3이고, kernel은 11 x 11 x 3이며, output feature map은 55 x 55 x 48이므로

parameters = 11 x 11 x 3 x 48 x 2 = 35K(34,848)이다.
여기서, 2는 AlexNet의 구조상 두 개의 네트워크 구조를 가졌기에 곱해진다.

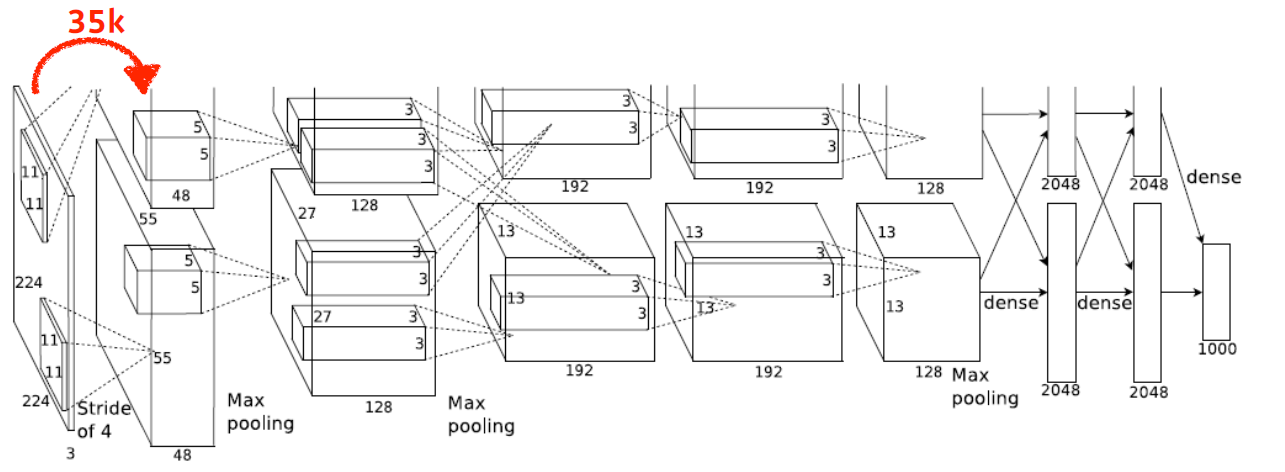
이후, 이전에 구한 첫번째 파라미터와 함께, 나머지 layer의 parameter는 아래와 같다. 결과를 보면 dense layer의 parameter가 conv layer의 1000배 가량 많은 것을 확인해볼 수 있다. 왜 그럴까?
Dense Layer는 모든 input에 대응되는 weight가 존재하지만, conv layer는 하나의 kernel이 모든 input에 대해 동일하게 작동하기 때문이다.

Convolution Layer
1. 11 x 11 x 3 x 48 x 2 = 34,848
2. 5 x 5 x 48 x 128 x 2 = 307,200
3. 3 x 3 x 128 x 2 x 129 x 2 = 884,736
4. 3 x 3 x 192 x 192 x 2 = 663,552
5. 3 x 3 x 192 x 128 x 2 = 442,368

Fully Connected Layer(Dense Layer)
6. 13 x 13 x 128 x 2 x 2048 x 2 = 177,209,344
7. 2048 x 2 x 2048 x 2 = 16,777,216
8. 2048 x 2 x 1000 = 4,096,000

결론적으로, generalization performance를 높이기 위해 conv layer는 점점 깊어지지만 dense layer를 최소화하여 parameter를 줄이려는 여러 방법들이 나오고 있다. 그 중 하나는 1 x 1 convolution이다.

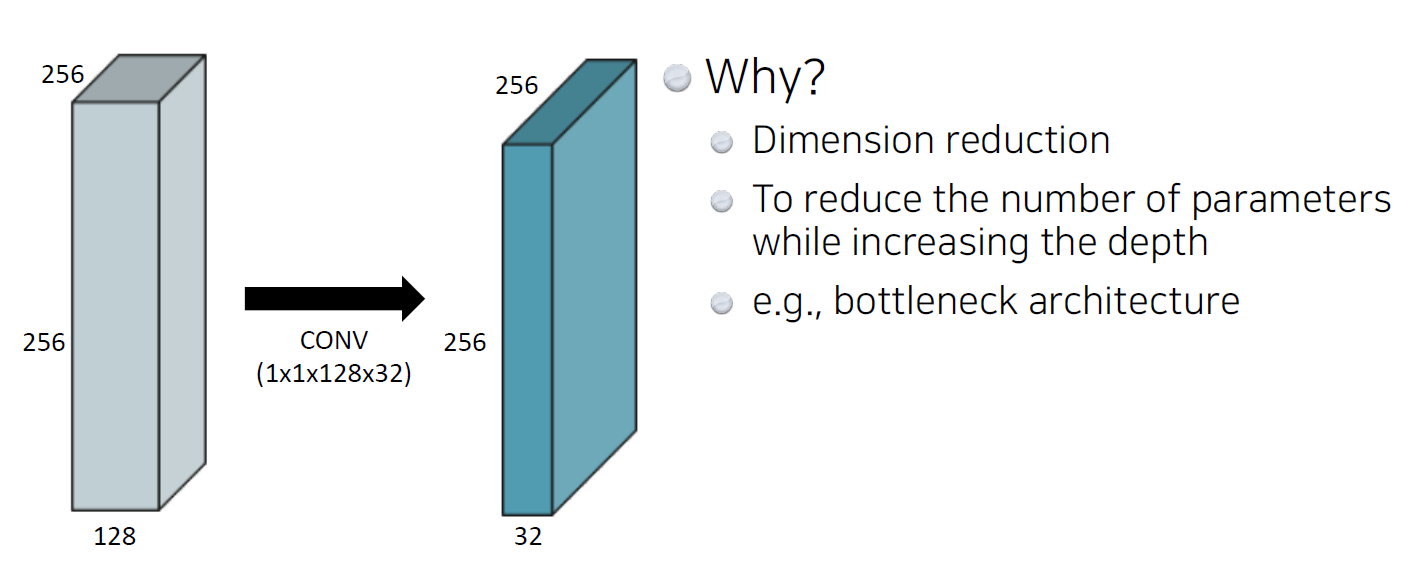
1 x 1 convolution은 image의 한 pixel만 보기에 이미지의 영역을 보는 것이 아니다. 그러면 왜 사용할까?

1. Dimension reduction
   • image의 크기(special dimension)는 유지한 채 Dimension을 줄이는 것으로, conv layer의 depth를 늘리는 동시에 파라미터 숫자를 줄일 수 있음
   • e.g., bottleneck architecture