경사하강법 이해를 위한 사전 지식 학습

미분(Differentiation)

• 미분은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용하는 기법

• $f'(x) = \lim_{n\to0}{f(x+h) - f(x)\over h}$ ※ 미분의 변화율은 극한(limit)으로 정의
  $f(x) = x^2 + 2x + 3 \overset{미분}{=}> f'(x) = \lim_{n\to0}{f(x+h) - f(x)\over h} = \lim_{n\to0}{(2x+2+h)} = 2x+2$

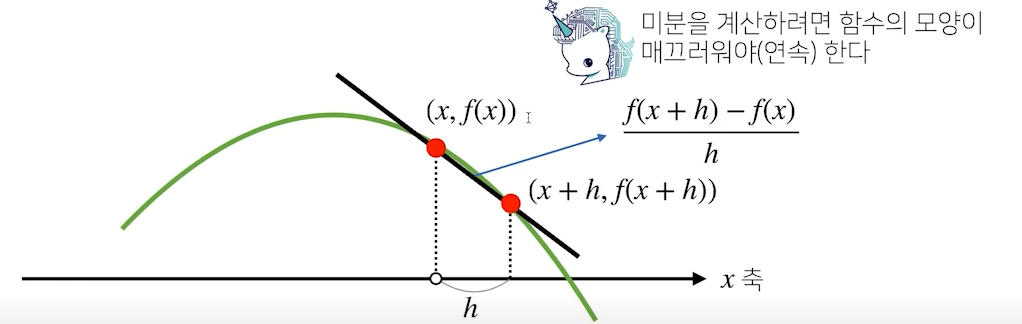
• 그림으로 보면, 미분은 함수 $f$의 주어진 점$(x,f(x))$에서의 접선의 기울기를 구하는 것

  • 미분을 계산하려면 값이 연속적이어야 함
  • $h$가 0으로 수렴하여 x에서의 접선의 기울기로 됨

    

• python으로 미분

  import sympy as sym #함수를 sumbol, 즉 기호로 인식
                      #sympy.diff 로 미분을 컴퓨터로 계산 가능
  from sympy.abc import x
  sym.diff(sym.poly(x**2 + x*2 + 3), x)
  >> Poly(2*x + 2, x, domain = 'ZZ')

  미분값 활용

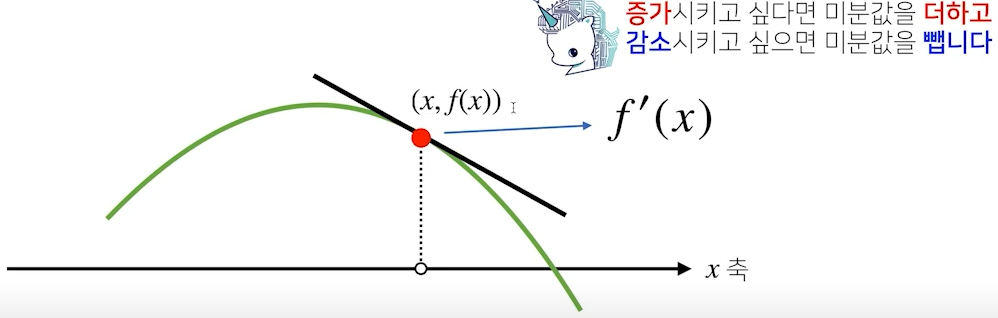
• 미분값이 주어졌을 때 어느 방향으로 움직어야 함수값이 증가 혹은 감소하는지를 알 수 있음

  

• 함수값을 증가시킬 경우 => $x+f'(x)$

  • 미분값이 음수일 경우 미분값을 더해주면 좌측으로 이동하여 함수값이 증가
  • 반대로, 미분값이 양수일 경우 미분값을 더해주면 우측으로 이동하여 함수값이 증가

• 함수값을 감소시킬 경우 => $x-f'(x)$

  • 미분값이 음수(아래 그림 참고)일 경우 미분값을 더해주면 우측으로 이동하여 함수값이 증가
  • 반대로, 미분값이 양수일 경우 미분값을 더해주면 좌측으로 이동하여 함수값이 증가

    

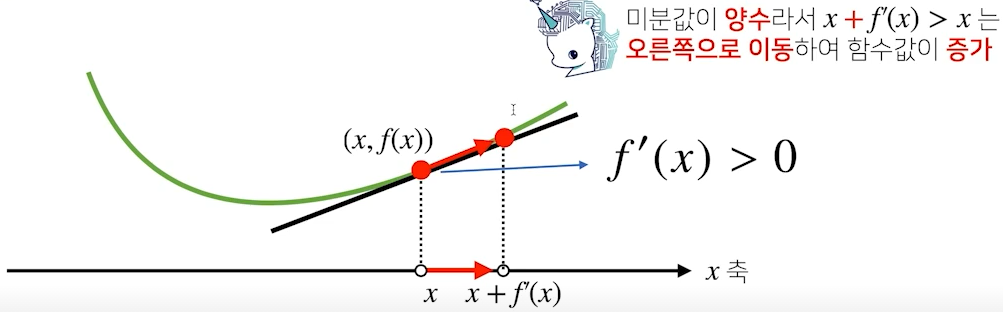
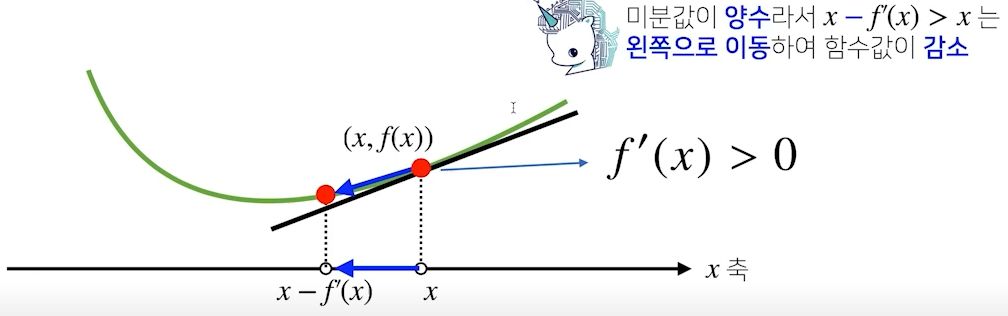
목적함수의 최대화를 위해 미분값을 더하면 경사상승법(gradient ascent)

목적함수의 최소화를 위해 미분값을 더하면 경사하강법(gradient descent)

※ 극값(최대,최소)에 도달하면, 즉 미분값이 0이 되면 업데이트가 종료

경사하강법 알고리즘

• 변수가 한개일 경우
  • gradient : 미분을 계산하는 함수
  • init : 시작점
  • lr(learning rate) : 학습률
    • lr을 통해 업데이트 속도를 조절
    • 해당 조건을 통해 실제 경사하강법 알고리즘이 최소값으로 수렴하는데 큰 영향을 미침
  • eps : 알고리즘 종료 조건
    • 실제로 컴퓨터가 계산 시 미분이 정확히 0이 되는 것은 불가하므로 eps 보다 작을 때 학습 종료

import numpy as np
import sympy as sym
from sympy.abc import x

def func(val):
    func = sym.poly(x**2 + x*2 + 3)
    return fun.subs(x,val), fun

def func_gradient(fun,val):
    _, function = fun(val)
    diff = sym.diff(function, x)
    return diff.subs(x,val) diff

def gradient_descent(fun, init_point, lr_rate = 0.01, epsilon = 0.00001):
    cnt = 0
    val = init_point
    diff, _ = func_gradient(fun, val)
    while np.abs(diff) > epsilon:
        val = val - lr_rate*diff
        diff, _ = func_gradient(fun, val)
        cnt +=1
    print("함수: {fun(val)[1]}, 연산횟수: {cnt}, chlthwja: ({val}, {fun(val)[0]})"

gradient_descent(fun = func, init_point=np.random.uniform(-2,2))

• 2차원 Input일 경우

  • 벡터 입력인 경우, 편미뷴(partial differentiation)을 사용

    $\partial_{x_{i}} f'(x) = \lim_{n\to0}{f(x+he_{i}) - f(x)\over h}$
    ※ $e_i$ 는 i번째 값만 1이고 나머지는 0인 단위 벡터
    ※$\partial_{x_{i}}$는 $X_i$ 변수로 값을 미분하라는 표시

  $f(x,y) = x^2 + 2xy + 3 + cos(x + 2y)$
  $x$에 대해 편미분 => $\partial_{x}f(x,y) = 2x + 2y + 3 - sin(x + 2y)$

• 2차원 Input일 경우

  • 다차원일 경우도 편미분을 사용하며
  • 각 변수 별로 편미분을 계산한 그레디언트(gradient)벡터를 이용하여 경사하강법(or 경사상승법)을 사용

    $\nabla f = ({\partial_{x_1}f, \partial_{x_2 }f,\cdots,\partial_{x_d}f)}$
    ※ $\nabla$ : nabla

  • 앞서 사용한 미분값 $f'(x)$ 대신 $\nabla f$를 사용하여 변수 $X = (x_1,x_2,\cdots,x_d$)를 동시에 업데이트 가능
  • 미분결과에 마이너스(-)를 곱해주면 극소점으로 가장 빨리 감소되는 방향을 알 수 있음, $-\nabla f = {\nabla (-f)}$
  • 예시) $f(x,y) = x^2 + y^2$, $-\nabla f = -(2x,4y)$

    

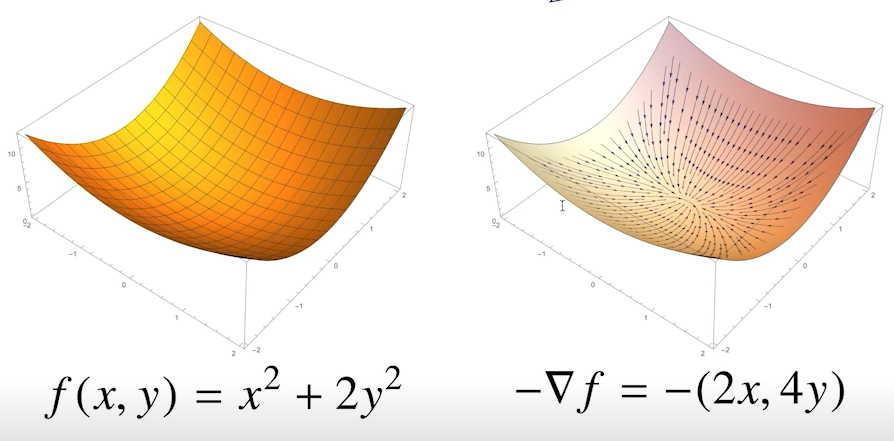
  • 다변수일 때는 미분값의 절대값 대신, norm을 계산하여 eps 조건 설정, 그 외 동일

import numpy as np
import sympy as sym
from sympy.abc import x

def func(val):
    x_, y_ = val
    func = sym.poly(x**2 + 2*y**3)
    return fun.subs(x,[x_, y_]), fun

def eval_(fun,val):
    val_x, val_y = val
    func_eval = fun.subs(x, val_x).subs(y,val_y)
    return func_eval

def func_gradient(fun,val):
    x_, y_ = val
    _, function = fun(val) #func 함수
    diff_x = sym.diff(function, x)
    diff_y = sym.diff(function, y)
    grad_vec = np.array([eval_(diff_x, [x_,y_]), eval_(diff_y, [x_,y_])])
    return grad_vec, [diff_x, diff_y]

def gradient_descent(fun, init_point, lr_rate = 0.01, epsilon = 0.00001):
    cnt = 0
    val = init_point
    diff, _ = func_gradient(fun, val)
    while np.linalg.norm(diff) > epsilon:
        val = val - lr_rate*diff
        diff, _ = func_gradient(fun, val)
        cnt +=1
    print("함수: {fun(val)[1]}, 연산횟수: {cnt}, chlthwja: ({val}, {fun(val)[0]})"

pt = [np.random.uniform(-2,2), np.random.uniform(-2,2)]
gradient_descent(fun = func, init_point=pt)