[cs231n] Lecture 2 | Image Classification 리뷰

Image Classification은 이전 강의에서도 설명했듯이 컴퓨터 비전의 core task 중 하나로, 이미지를 입력으로 받으면 이를 주어진 카테고리 중 하나로 분류하는 작업을 의미합니다.

말로만 들으면 음? 그냥 간단한 task네 싶을 수 있지만, 이 작업은 사실 굉장히 어렵고 복잡한 작업입니다.

우선 컴퓨터는 우리 눈과 달리 이미지를 RGB값들에 대한 숫자들의 모임, 즉 행렬로 인식합니다. 800X600 사이즈의 사진은 컴퓨터에게 있어 800X600X3 개의 숫자들의 모임으로 이루어진 거대한 텐서로 인식된다는 의미이죠.

또한 사진을 찍은 카메라의 시점(viewpoint)가 어디에 있느냐에 따라서, 각 픽셀에 해당하는 값들이 크게 변화하게 됩니다. 알고리즘은 이러한 시점 변화에 의한 pixel값의 변화에도 늘 robust(강건)하게 물체를 분류할 수 있어야 합니다.

또한 밝은 곳에서 바라본 물체는 밝아보일 것이고, 그늘진 곳에서 바라본 물체는 어두워보이겠죠? 그리고 같은 물체라도 여러 pose를 취할 수 있을 것입니다(고양이라 치면 서있는 모습, 누워있는 모습, 앉아있는 모습 등...). 그리고 물체의 일부 또는 상당수가 어떤 다른 물체에 가려져있을 수도 있고, 배경과 물체가 비슷한 색상이라 구별이 어려울 수도 있습니다. 또 같은 물체라도 조금씩 생긴 게 다를수도 있죠. 고양이라고 해서 다 치즈색 고양이만 있는 게 아니라 검은색, 회색 고양이도 있듯이 말이죠!

이러한 점들 때문에 이 Image Classification은 결코 쉬운 task라고 말 할 수 없습니다.

Image Classifier

알고리즘 전공 수업을 들으면 가장 처음 접하게 되는 정렬 알고리즘들과 다르게, Image의 class를 구분하는 task에는 명확한 알고리즘이 존재하지 않습니다.

Image Classification을 위해 이전까지 제시되었던 대표적인 알고리즘에 대해 소개해보자면, 사진에서 edge를 1차적으로 판별하고, corner를 판별하여 이미지를 분류하는 알고리즘이 존재했습니다. 즉 모서리의 위치와 구조를 가지고 이미지를 구별하는 것이죠. 이는 앞서 말했듯이 viewpoint나 pose에 따라 크게 달라지기 때문에 robust하기 어렵습니다.

명확하게 수도 코드로 표현할 수 있는 classifier 알고리즘을 만들기 어렵다는 점에 도달하자, 사람들은 Data 기반의 접근을 하게 되었습니다. image와 label이 정리된 dataset을 수집하고, 이 dataset을 기반으로 classifier를 머신 러닝을 통해 새로운 이미지를 잘 구별할 수 있도록 학습시키는 방법이죠. 이 Data-driven Approach를 통해 이전보다 robust한 출력을 기대할 수 있게 되었습니다.

Classifier: NN(Nearest Neighbor)

인공지능, 머신러닝에 대해 공부해 본 사람들이라면 가장 처음 배우게 되는 정말 간단하고 기본적인 구조입니다.

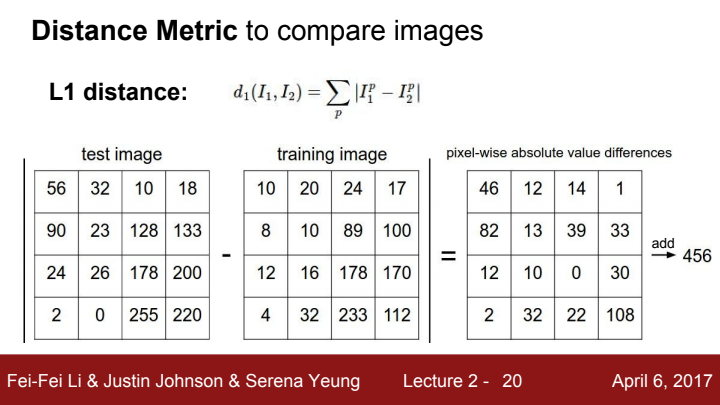
이 NN에 사용되는 개념인 Distance Metric에 대해 먼저 알아보겠습니다. 이전에서 이미지는 컴퓨터에게 있어 행렬로 인식된다고 언급했었죠? 두 이미지를 비교할 때, 한 이미지의 행렬 값에서 다른 이미지의 행렬 값을 pixel-wise difference를 해준 후 절대값을 취한 뒤, 모든 pixel에 해당하는 절대값들을 더해준 값을 L1 distance, 또는 Manhattan distance라고 표현합니다.

NN이란 한 이미지의 label을 주변 이미지들 중 L1 distance값이 가장 작은 이미지의 label과 같다고 분류하는 알고리즘입니다.

L1, L2 등의 용어에 대해선 뒤에서 좀 더 설명될 예정이니 일단은 이 L1의 정의가 무엇인지 정도만 이 강의에서 알아두시면 될 거 같습니다!

위 사진에서 NN을 train하고 test하는 코드를 확인할 수 있는데요. train 함수와 predict함수를 확인해보면 train의 시간 복잡도는 O(1), predict의 시간 복잡도는 for문으로 인해 O(N)임을 확인할 수 있습니다. 이는 좋지 않습니다. 왜냐면 우리는 비록 train의 시간이 느릴지언정 test 과정에서는 빠르게 값을 도출할 수 있어야 하기 때문이죠. test time이 길다는 뜻은 이 모델이 real time에서 실행되지 못한다는 점을 시사합니다. 즉 실용적이지 못하다는 거죠.

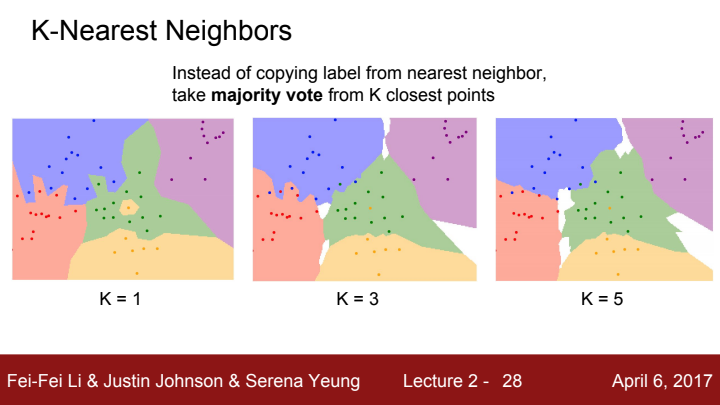
위 사진에서 K=1일 때가 지금까지 배운 NN 알고리즘이라 볼 수 있습니다. 한 가운데에 혼자 섬처럼 고립된 노란색 label이 보이시죠? 저 위치는 초록색으로 보는 것이 타당한데, 가장 가까운 한 이웃끼리만 같은 label로 분류하다보면 저렇게 island가 생기기 쉽습니다. 또한 label끼리의 boundary도 다소 작위적이죠.

이 NN을 보완한 아이디어가 바로 k-NN(k-초근접 이웃)입니다. K개의 인접한 점들에서 각각의 label을 투표를 하여 가장 많은 표를 받은 label로 분류하는 아이디어인데요. K의 수가 늘어날수록 label들의 boundary가 smooth해지는 것을 확인할 수 있습니다. 또한 위 사진에서 흰 색으로 표시된 부분은 어떤 label에도 포함되지 않는, point가 존재하지 않는 지역으로 해석할 수 있습니다.

또한 점들끼리의 distance를 비교할 때, L1 이외에도 여러 distance를 사용할 수 있습니다. L1 distance가 점끼리의 거리의 절대값들의 합이었다면, L2는 두 점의 차이를 제곱해준 뒤, 그 제곱값들을 모두 더해 루트를 씌워준 값입니다. 이를 수학에서는 노름(norm)이라고 명명합니다.

Lp distance는 아래와 같이 수식으로 표현할 수 있습니다. (p는 1 이상의 자연수)

K=1일 때 NN에서, L1 distance가 아닌 L2를 사용해준다면 조금 더 natural한 label끼리의 boundary를 얻을 수 있습니다.

우리가 NN 알고리즘을 사용해 Image classification을 수행하기로 결정했다면,

• K의 값을 얼마로 결정해야 할지
• 어떤 distance를 사용해야 할지(L1, L2 ...)

등에 대해 직접 결정해주어야 할 것입니다.

이처럼 알고리즘에서 학습을 통해 update되는 parameter가 아닌 사람이 직접 setting해줘야 하는 값을 하이퍼파라미터(hyperparameter)라고 합니다.

이 하이퍼파라미터를 적절히 세팅하는 방법으로는,

• 데이터를 train, val, test set으로 나눈 뒤 train set으로 학습을 시키고, val set에서 최적의 값이 나오도록 하이퍼파라미터를 조정한 뒤 test set을 통해 evaluate하기
• train set 데이터를 몇 개의 fold로 나눈 뒤 각 fold를 마치 위에서 언급한 val set처럼 사용해 하이퍼파라미터를 조정해보고, 전체 fold에서 조정한 하이퍼파라미터 값의 average를 사용해 test set에서 evaluate하기 (Cross-Validation)

두 가지의 방법이 있습니다. 첫 번째 방법은 dataset의 크기가 클 때 사용하면 좋은 방법이고, 두 번째 방법은 dataset의 크기가 상대적으로 작을 때 활용할 수 있는 방법입니다. 다만, 딥러닝을 학습하기 위한 dataset의 크기는 보통 매우 크기 때문에 Cross-varidation을 거의 사용하지 않습니다.

실제로 K-NN 알고리즘은 Image Classification에 잘 사용되지 않습니다. 그 이유는 앞서 언급되었듯이 test time이 너무 오래 걸리기도 하고, 이미지 간의 distance라는 게 이미지 사이의 유사성을 썩 잘 설명하지는 못하기 때문이죠. 위 사진에서 보면 맨 왼쪽 사진과 같은 L2 distance를 가진 3가지 사진을 제시하고 있습니다. 이미지에 여러 가지 변환을 주었는데도 다들 distance가 같다는 사실을 확인할 수 있습니다. 이미지를 제대로 분류하기 위해선 더 좋은 기준이 필요할 것입니다.

또한 차원의 저주라는 문제 때문에도 k-NN을 사용하기 쉽지 않은데요. 점들을 잇는 선의 경우 1차원이기 때문에 다른 두 선의 distance를 구하는 데에 별 문제가 없겠지만, 우리가 사용하는 이미지는 RGB 채널로 이루어진 행렬들의 모임, 즉 3차원 텐서라고 했었습니다. 다른 두 텐서의 distance를 구하기 위해선, 엄청나게 많은 pixel들을 가지고 distance를 구해야 합니다. 계산 비용이 엄청나지겠죠?

그래서 우리는 NN보다 더 나은 classifier를 사용할 것입니다.

Linear Classification

Linear classifier는 Nerual Network를 구성하는 중요한 블럭 중에 하나입니다. 이 Linear Classifier를 통해 이미지의 category를 분류하거나, NLP와 Computer Vision이 결합된 Image captioning 등의 task에서도 특정 단어를 RNN이 분류할 수 있게 해줍니다. (사실 이후에 배우게 될 RNN을 공부하면 이 말이 아주 엄밀하지는 못한 워딩임을 알 수 있지만... 일단 그렇다 치고 넘어갑시다)

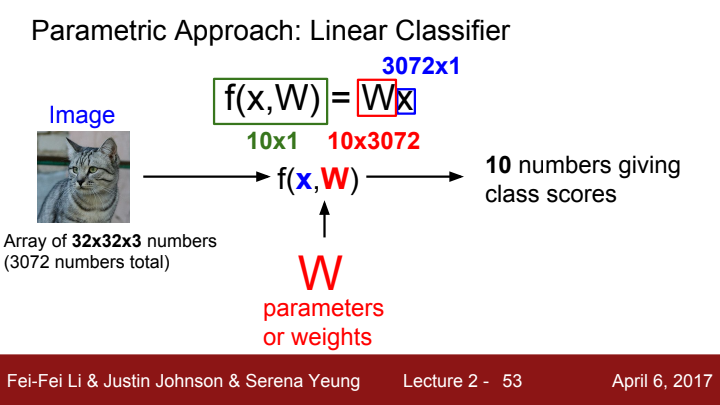
입력 x와 가중치 행렬 W을 input으로 하는 linear classifier의 score function f(x, W)는 가중치에 입력을 곱한 값 Wx입니다. 위 사진을 예시로 들 때, 사진을 구성하는 pixel의 수는 총 3072개임을 확인할 수 있습니다. 분류해야 할 category의 개수가 10개라고 치면, 우리가 원하는 출력값의 크기는 10x1 크기의 벡터입니다. 이 값을 걷기 위해선 행렬 W이 10x3072의 size를 가져야겠죠?

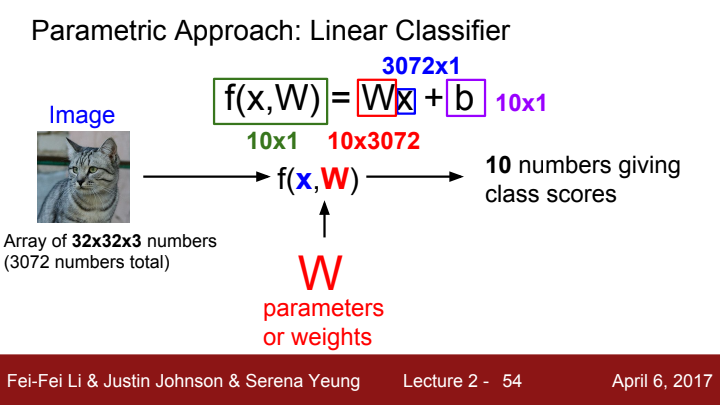
보다 정확한 classification을 위해 bias를 추가해줄 수도 있습니다.

위의 설명들에 대한 예시를 보여주고 있습니다. 사진의 각 픽셀 값에 가중치 행렬 W를 곱해주고 bias를 더해 각 클래스에 대한 score를 값으로 가지는 벡터를 출력으로 얻게 되었습니다. 여기서 W와 b의 초기값은 랜덤하게 정하는 것이 보통이며, 모델의 성능을 개선하고 loss function 값을 줄이기 위해 랜덤한 가중치 값들이 gaussian 분포를 가지도록 설정을 하는 등의 skill을 사용할 수 있습니다(이후 강의에서 소개될 예정입니다. 무슨 말인지 이해가 안 되더라도 걱정 마세요!).

Linear Classifier를 보기 쉽게 그래프로 표현한 모습입니다. bias의 존재로 인해 선들의 y절편이 0이 아니게 됨으로써 보다 정확한 분류를 할 수 있게 된 모습을 확인할 수 있습니다.

Linear Classifier는 NN보다는 비교적 정확하고 natural한 분류를 할 수 있지만, 한 개의 직선만으로 정확하게 두 그룹을 분리할 수 없는 경우가 있을 수도 있습니다. 두 번째와 세 번째 사진의 경우가 바로 그 경우인데요.
예를 들어 dataset에 말 사진과 label이 있다고 쳤을 때 이미지의 왼쪽에 말의 머리가 있는 말 사진이 있을 수 있고, 오른쪽에 말 머리가 있는 사진이 있을 수도 있습니다. 단일 classifier만을 가지고 이미지를 분류하게 될 경우, classifier는 말이라는 객체를 왼쪽과 오른쪽 모두 머리가 있는 동물로 인식할 문제가 발생할 수 있죠. 그렇기 때문에 linear classifier를 하나만 가지고 image를 분류하는 것은 위험(?)합니다.

지금까지 Image Classification의 개념과 Classifier의 종류 및 원리에 대해 알아보았습니다. 다음 강의에선 linear classifier의 score function의 가중치가 얼마나 좋은 값을 가지는 지를 알 수 있는 척도인 loss function, loss가 최소화되도록 하는 최적의 W 값을 찾는 과정인 optimization, linear classifier의 변형된 과정이자 우리가 CNN이라 부르는 ConvNet에 대해 알아보도록 하겠습니다.