[cs231n] Lecture 3 | Loss Functions and Optimization 리뷰
지난 시간엔 Image classification과 NN, Linear classifier 등에 대해 배웠습니다.

지난 시간에 미처 정리하지 못한 내용들을 정리하자면, Linear classifier를 정의한 이후에 최적의 W값을 찾기 위해선
- training data를 가지고 classifier가 출력한 score function이 얼마나 정답에 대해 만족하지 못하는지를 수량화해주는 Loss function을 정의한다.
- loss function을 최소화시키는 가중치 행렬(+bias)의 parameter를 효율적으로 찾을 수 있는 방법을 고안한다(Optimization).
위 두 과정을 거쳐야 합니다. 이 Loss function과 optimization이 이번 강의에서 우리가 다룰 내용이 되겠습니다.
위 사진에서 보면 각 사진에 대한 정답인 고양이, 차, 개구리에 대한 score vector를 확인할 수 있습니다. 두 번째 사진의 경우 정답인 car의 score가 가장 높은 것으로 보아 차에 대해선 classifier가 잘 분류를 하지만, cat은 score 값이 상대적으로 낮고, frog은 심지어 정답이 나와야 할 frog class의 score가 음수가 나와버리는 것을 확인할 수 있습니다.
이처럼 잘못된 W값에 따라 모델이 classification을 잘 하지 못 할 수도 있습니다. 우리는 이런 문제를 해결하기 위해 얼마나 W값이 잘못되었는지를 수량화하는 loss function을 정의하고, 이 loss function이 최소화되도록 optimization을 거쳐야합니다.
Loss functions

loss function의 수식은 다음과 같이 정의할 수 있습니다. score function 값을 통해 예측한 값과 label(정답) 사이의 관계를 설명하는 loss function을 정의하고 이를 sum해준 뒤 data의 개수로 나누어줍니다.
Multiclass SVM loss

loss function 중 하나인 Multiclass SVM loss에 대해 설명드리도록 하겠습니다. 수식은 위에 나와있는 식과 같습니다. s_j는 정답 레이블을 제외한 클래스들의 score, s_yi는 실제 레이블에 해당하는 score 값을 의미합니다. 예시로 위 사진에서 첫 번째 고양이의 경우 s_yi가 3.2, s_j는 5.1과 -1.7이라는 것을 확인할 수 있습니다.

그래프의 x축 값을 s_yi, y축을 loss라고 했을 때, 수식의 정의 상 s_j보다 s_yi이 1 이상으로 더 큰 값을 가지면 loss값이 0이 되기에, loss를 그래프로 그리면 위와 같이 hinge 형태를 보이는 것을 볼 수 있습니다.
L = max(0, s_j - s_yi + 1) 이 수식임을 상기해보세요!



각 이미지에 대해 classifier가 출력한 score vector를 가지고 loss들을 구하는 과정입니다. 파란색으로 쓰여진 수식 풀이 과정을 보니 Multiclass SVM loss를 구하는 과정이 조금 더 이해가 가죠? 두 번째 car의 경우 이미 차를 잘 분류하고 있기 때문에 loss 값이 0이 나오는 것을 확인할 수 있습니다. 세 번째 개구리의 경우 frog의 score가 음수가 나오기 때문에 loss 값이 매우 높게 나오는 것을 볼 수 있습니다.
Loss는 값이 작을 수록 좋습니다. 우리의 목표는 Loss가 0에 가능한 한 수렴하도록 모델을 학습시키는 것이 목표입니다.

마지막으로 각 데이터에 대한 Loss들을 모두 sum한 뒤 데이터의 총 개수(여기선 3개)로 나눠줌으로써 최종적인 Loss를 구하게 됩니다.
Q. 만약 2번째 사진에서의 car score의 값이 살짝 낮아지거나 높아지면 어떻게 되나요?
A. 값이 아주 살짝 바뀌는 것이라면, 수식 상 loss값은 그대로 유지될 것입니다.
Q. loss값의 min/max 값은 이론 상 얼마일까요?
A. 최소값은 0, 최대값은 무한대 입니다.
Q. 만약 가중치 행렬의 모든 값이 매우 작아 모든 s값이 0에 가깝게 나온다면 loss값은 어떻게 될까요?
A. 'class 개수 - 1' 이 나오게 됩니다. 수식 상 모든 loss 값이 1이 나오게 될 거고, 정답 class를 제외한 모든 class에서의 loss값들을 더한 값이 Multiclass SVM loss의 정의이기 때문입니다.
Q. 만약 loss의 정의를 모든 클래스의 loss의 합으로 바꾼다면 어떻게 될까요?
(즉, 정답 class에 대한 loss까지 모두 더해준다면 어떻게 될까요?)
A. loss += 1을 해준 값이 될 것입니다. s_j = s_yi이기에 정답 레이블에 해당하는 class의 loss는 1일 것이기 때문입니다.
Q. 만약 sum 대신 mean을 사용해준다면 어떻게 될까요?
A. 값이 scaling 되는 것 뿐, 크게 차이는 없습니다.
Q. 만약 max(0, s_j - s_yi + 1)^2 를 사용한다면 어떻게 될까요?
A. 아예 다른 알고리즘이 될 것입니다. 기존 loss와 달리 값이 비선형적으로 변하기 때문에 같은 score를 가지고 loss를 구하더라도 그 값이 확연히 차이가 날 것이기 때문입니다. 또한 차후에 배울 backpropagation 과정에서도 gradient가 다르기에 큰 차이가 있을 것입니다.

만약 L=0으로 만드는 W를 찾았다고 가정해봅시다. 그럼 이 W는 유일하게 L=0을 만드는 행렬일까요? 정답은 아닙니다. W을 a배 scailing해준 수 많은 aW들 또한 L을 0으로 만들어 줄 것입니다.
Overfitting
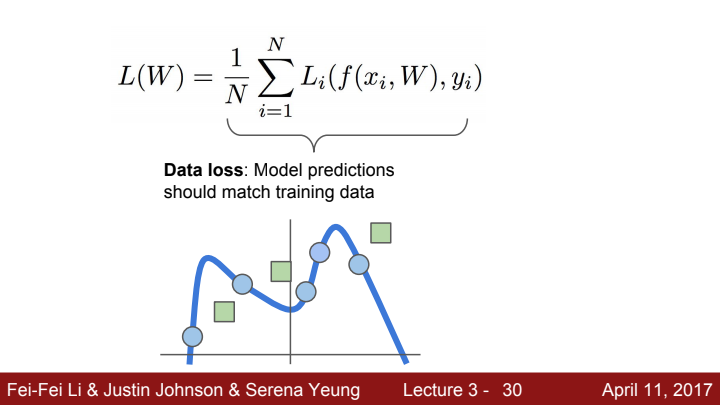
해당 Loss를 가지고 모델을 학습시킬수록, model은 training data에 맞도록 예측값을 내놓게 됩니다. 이는 얼핏 듣기에 좋은 말처럼 들릴 수 있지만, 위 사진처럼 새로운 데이터(초록 사각형)이 들어왔을 때 원하는 매칭값을 찾기 어려워 질 수 있다는 문제가 있습니다. 이러한 현상을 overfitting이라고 합니다.
우리는 모델이 training data에 overfitting하는 것을 막아야 합니다! 우리가 원하는 모델은 train set에 대해 완벽한 정답을 맞추는 모델이 아닌, train set에 대한 정확도가 다소 떨어지더라도 test 단계에서 보다 general한 prediction을 할 수 있는 모델이기 때문입니다.
Regularization

Loss가 train set에 overfitting하는 것을 막기 위해, Regularization term을 loss 수식에 추가하는 방법을 사용할 수 있습니다. 이 Regularization term은 오직 W에 대한 간단한 구조의 함수값인데요, W가 train set에 맞도록 overfitting이 되게 학습이 되려고 한다면 regularization term의 값이 커지게 되어 전체 loss 값이 상승하게 됩니다. 즉 data loss의 학습 방향과 모순을 일으킨다고 볼 수 있습니다. 모델 학습은 총 loss값이 최소값이 되도록 하는 방향으로 이루어지기 때문에, overfitting이 이뤄지지 않는 선에서 균형을 맞추도록 가중치 값이 update될 것입니다.
이 아이디어는 '오컴의 면도날'이라는 이론에서 착안되었다 볼 수 있는데요. 오컴의 면도날이란 '한 문제에 대한 여러 가지 가설이 있다면, 그 중 가장 간단한 것이 최고다'라는 내용의 이론입니다.(정확한 설명은 아니겠지만, 그냥 대충 이렇다 정도로 넘어갑시다) Regularization term을 통해 model이 train set에 정확히 맞춰지는 복잡한 구조를 가지는 것이 방지되고 보다 간단하고 general한 구조를 가지게 됩니다.

Regularization은 쉽게 이야기하자면 panelty term(=Regularization term)을 통해 model의 복잡성을 규제하는 것을 의미합니다. panelty term에 곱해지는 lambda는 regularization strength라 불리우며, 얼마나 강한 규제를 내릴지를 결정해주는 하이퍼파라미터입니다. 이 lambda 값이 매우 크다면, 가중치 행렬 W는 data loss term보다 regularization term의 크기를 줄이는 방향으로 update가 될 것이고 이는 즉 regularization term의 그래프에 가까운 형태의 loss 그래프를 얻을 수 있다는 의미일 것입니다.
regularization을 할 때 보통 L2 regularization을 사용하곤 합니다. L1, L2가 무엇을 의미하는지는 이전 강의에서 다룬 적 있죠? L2 loss와는 조금 다른 게 여기서의 L2는 제곱 후 sum을 한 뒤 루트를 씌우지 않습니다. 이 외에도 dropout, batch normalization, stochastic depth 등의 fancy한 방법들도 많이 사용되곤 합니다. 일단은 L2 regularization에 대해 주로 다뤄보도록 하겠습니다.
L2 regularization(Weight decay)

L2 regularization을 자세히 설명해보자면, 위의 수식처럼 가중치 행렬의 모든 element들을 제곱하여 더한 값입니다. Linear classifier의 경우 위 사진에서 w1, w2 모두 같은 값인 1이 나오게 될 것입니다. 하지만 regularization term의 경우, w1보다 w2를 더욱 선호하게 될 것입니다.
일단 의미론적으로 보자면 가중치가 고르게 분포되어 있을수록 한 element에 대한 영향보단 vector 전체에게 골고루 영향을 받기 때문에 w2가 더욱 선호될 수 있다고 생각할 수 있습니다. 특정 위치(pixel)의 element가 강한 값을 가지는 data에게 overfitting되는 것을 방지한다고 생각할수도 있겠군요!
또한 직접 L2 regularization을 구해본다면 w1은 1, w2는 4 * (0.25)^2 = 0.25 가 나오게 됩니다. 둘 중에 최종 loss 값이 더 작아지게 만들어주는 w2를 선호할 수 밖에 없다는 걸 수식적으로도 확인할 수 있습니다.
(베이지안이라 적힌 부분의 내용은 어렵기도 하고, 저도 아직 공부가 덜 된 부분이기 때문에 추후 확률 통계나 머신러닝 이론을 추가로 이 블로그에 정리하여 보도록 하겠습니다. 만약 제가 까먹지 않는다면...)
Softmax Classifier
지금까지 우리가 다룬 classifier는 linear classifier입니다. 하지만 단순한 선형으로는 data를 정확하게 분리하기 힘들 수 있습니다.
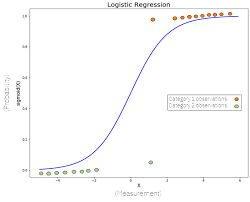
위 사진에서 데이터의 분포를 보면, 단순히 선형으로 두 데이터의 영역을 구분짓기보단 저렇게 S자 형태의 그래프(Sigmoid)로 데이터를 분류하는 것이 더욱 합리적으로 보입니다. 이와 같이 선형이 아닌 log 형태의 그래프로 regression을 하는 것을 logistic regression이라고 합니다.
참고! 머신 러닝 모델은 크게 두 가지의 종류가 있습니다.
classifier: 주어진 데이터의 카테고리로 분류하는 모델
regressor: 주어진 입력과 출력 관계를 설명하는 함수 식을 찾는 모델
classification은 출력 값을 찾는 과정, regression은 함수 관계를 찾는 과정이라고 볼 수도 있습니다.

Softmax Classifier의 score가 의미하는 바는 각 class에 대한 normalized되지 않은 log probability(말 그대로 unnormalized probability 값에 로그를 취한 것)를 의미합니다. 이 score를 normalize 해주는 함수가 바로 softmax function입니다. softmax function을 거친 후 얻게 되는 vector의 값이 바로 이미지가 해당 class에 해당될 확률이 되는 것입니다.

classifier가 보다 정확하게 분류를 하기 위해선 정답 class에 해당하는 log likelihood의 값이 최대가 되게 하거나, 혹은 negative log likelihood 값이 최소가 되게 해야합니다. 이러한 수행을 하기 위하여 우리는 위에서 정의된 수식인 Cross Entrophy라는 loss를 사용합니다.
왜 마이너스가 log 앞에 붙냐고 한다면, 확률이라는 것은 값이 0~1 사이이기 때문에 log를 태우면 음수가 나오기 때문입니다. 마이너스를 앞에 붙임으로써 마이너스 부호를 상쇄해 늘 0 또는 양수 값을 가지도록 하기 위함이죠.

수식이 진행되는 흐름을 보니 한 층 더 이해가 되는 것 같죠? 이 사진의 label은 cat이기 때문에, cat의 score 값이 커지고 나머지 score가 적어질수록 cross entrophy loss값이 줄어들게 될 것입니다.
Q. loss 값의 최대/최소값은 무엇인가요?
A. 확률값이 1일 때 최소값인 0, 확률값이 0일 때 최대값인 무한대를 가집니다.
Q. W 초기값이 작아 모든 s값이 0에 가깝게 나온다면 어떻게 되나요?
A. loss값이 무한대에 가깝게 나올 것입니다. 이를 가지고 backpropagation을 한다면 굉장히 큰 보폭으로 가중치가 업데이트가 되겠네요.

Softmax의 loss인 cross entrophy와 SVM의 loss인 hinge loss를 비교해보겠습니다. Softmax classifier의 loss는 정답 클래스는 무한대, 오답 클래스는 마이너스 무한대의 값을 가지도록 학습시킵니다. 즉 마음만 먹으면 무한대로 학습시킬 수 있습니다. 반면에 hinge loss는 SVM의 정답 클래스의 스코어와 예측 클래스의 스코어를 같게 하도록 학습시킵니다. 즉 학습이 계속되다보면 더 이상 학습이 되지 않는 지점에 이르게 됩니다.

지금까지 배운 내용에 대한 Recap입니다. 우리는 loss를 통해 가중치 W의 값들이 얼마나 좋은지 나쁜지를 판단할 수 있었습니다. W값에 대한 평가를 내린 후에는 그럼 어떻게 해야 최적의 W값들을 찾아갈 수 있을까요?
Optimization
optimization은 한 마디로 어떻게 W 값을 최적화시켜 나갈지에 대한 방법을 의미합니다.
W값이 우리가 원하는 결과를 도출할 수 있도록 최적화하기 위한 여러 전략들에 대해 소개해보겠습니다.
1. Random search
가장 안 좋은 방법입니다. W 행렬을 랜덤하게 생성한 후 loss를 구한 뒤, loss 값이 가장 최저값을 가질 때까지 반복해서 W 행렬을 다시 랜덤으로 초기화하고 loss를 구해 이전 loss와 비교합니다. 운이 참 좋으면 얼마 되지 않아 최적의 w값을 찾을 수 있겠지만, 그럴 확률이 희박하다는 건 깊게 생각해보지 않아도 알 수 있죠?
2. Follow the slope
최적의 W값을 구하는 과정을 흔히 협곡을 따라 내려가는 과정에 비유하고는 합니다. 현재 나의 위치는 loss function의 값, W의 값은 현재 모든 지점에서 보이는 풍경을 의미합니다. 우리의 목적은 협곡 맨 아래로 내려가는 것, 즉 loss의 값을 최소화하는 것입니다. 최대한 빠르고 확실하게 맨 아래로 내려가기 위해선 현재 내가 볼 수 있는 풍경 중 가장 기울기가 아래로 가파른 방향으로 걸어가야겠죠?
머신 러닝을 통해 학습시키고자 하는 모델의 입력은 1개가 아닌 여러 개입니다. 다변수 함수라고 볼 수 있죠. 다변수 함수에서 각 dimension 방향으로의 기울기 vector를 gradient라고 부릅니다.
각 방향으로의 slope는 각 방향에 gradient를 dot product한 값입니다. 가장 가파른 descent를 할 수 있는 방향은 gradient 값이 negative인 방향이겠죠? (gradient가 양수라면 계곡을 오히려 타고 올라가는 게 되기 때문입니다)

각 W에 대한 gradient를 numerical하게 계산하는 과정을 보여주고 있습니다. 함수 f를 loss로 정의하여 매우 작은 h만큼의 보폭의 차이만큼의 평균 기울기를 구하는 모습이죠?


다른 W의 원소들에 대한 gradient를 구하는 과정들입니다. 이러한 방법은 너무 느리고, 매 gradient를 구할 때마다 이렇게 계산을 하고 있으면 비용이 너무 많이 들 것입니다. 그리고 애초에 고등학교 수학 과정 및 대학 수학을 배운 우리로써는 이 과정이 본능적으로 답답하게 느껴질 것입니다. 당연하죠.

왜냐면 우리는 미적분 공식이라는, gradient를 구하는 최적의 tool을 알고 있기 때문입니다. 위와 같이 수치적으로 구한 기울기를 numerical gradient라고 한다면, 미적분을 이용해 계산한 gradient는 analytic gradient라고 합니다.
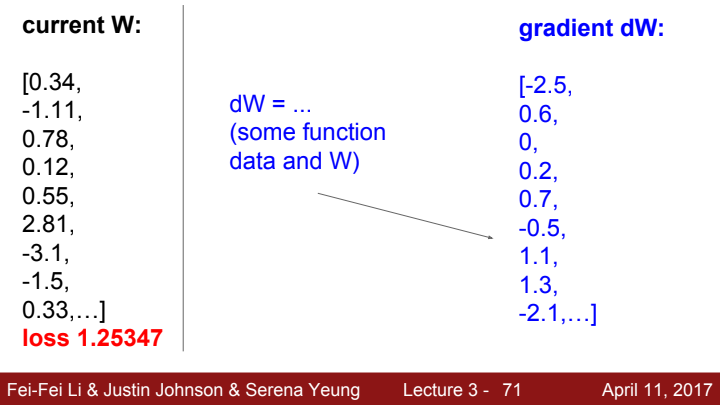
analytic gradient를 구하는 과정입니다. loss가 어떤 함수인지에 따라 각 방향으로의 gradient를 구할 수 있는 분석적인 expression을 미리 정해두고, 나중가선 W 값만 그 expression에 대입해 쉽게 gradient를 구해줍니다.
Q. 그러면 numerical gradient는 앞으로 사용할 일이 없겠네요?
A. 아닙니다. numerical gradient는 느리고 정확한 값이 아닌 근사값이지만, analytic gradient의 결과값이 error없이 잘 출력되고 있는지를 확인하는 데에 있어 유용한 tool이 되어줍니다. numerical gradient를 debugging 과정에서 사용해 implementation을 check하는 과정을 gradient check이라고 합니다.
Gradient Descent(GD)
def Gradient_Descent(step_size): #step_size는 hyperparameter
weights_grad = evaluate_gradient(loss, data, weights) #gradient를 우선 구해준다.
weights += -step_size*weights_grad Gradient Descent 아이디어의 코드를 간단하게 구현해보았습니다. 하이퍼파라미터인 step_size는 learning rate(학습률)이라는 이름으로 더욱 많이 불립니다. 매 backpropagation 과정에서 각 weights에 대한 gradient를 구해준 뒤, 이를 -learning rate에 곱한 만큼 더해줍니다.
weights -= step_size * weights_grad
weights += -step_size * weights_grad 왜 위의 식대로 적지 않고 아래처럼 굳이 (-)부호를 통해 수식을 정의했는지에 대해 의문이 드실 수 있습니다. 사실 위의 것처럼 코드를 작성해도 똑같이 돌아가기야 하겠지만... 아래의 수식이 우리가 Gradient Descent를 하는 의미와 조금 더 부합하기 때문에 저렇게 표현을 하는 것인데요.
우리는 앞서 계속 설명했듯이 gradient가 negative한 방향으로 발걸음을 내딛어야만 합니다. 그래야 loss의 최소값에 가까워지기 때문이죠. gradient가 negative할 때엔 해당 방향으로 나아가야 하기 때문에 (-)부호를 통해 negative를 상쇄시켜 가중치의 값을 증가시키고, gradient가 positive할 때는 우리가 경사를 거슬러 올라가고 있다는 의미이기에 (-)부호를 통해 가중치를 감소시켜 계곡의 골짜기로 향하도록 발걸음을 돌려줍니다.
step_size, 즉 learning rate가 의미하는 바는 바로 매 걸음마다 골짜기로 향하는 보폭의 크기를 의미합니다. 보폭의 크기가 만약 너무 크다면 어떻게 될까요? 최저점에 1m 거리밖에 남지 않았는데 내 보폭이 2m로 고정되어 있다면 우리는 결코 최저점에 도달할 수 없을 것입니다. 늘 최저점을 넘어 1m 만큼 더 이동할 수 밖에 없기 때문이죠.
반대로 보폭의 크기가 너무 작다면 어떻게 될까요? 최저점까지 100m가 남았는데 내 보폭이 1mm밖에 안 된다면, 최저점에 언젠간 확실히 도달할 수 있겠지만 도착하는 데 한 세월이 걸릴 것입니다...
이러한 이유로 learning rate 또한 신중하게 값을 결정해줘야 하는 중요한 hyperparameter이고, scheduler 등 이 hyperparameter를 optimization 하는 여러 방법들이 존재합니다. 이러한 방법들에 대해서는 추후 다룰 다른 강의들에서 확인하실 수 있을 것입니다.
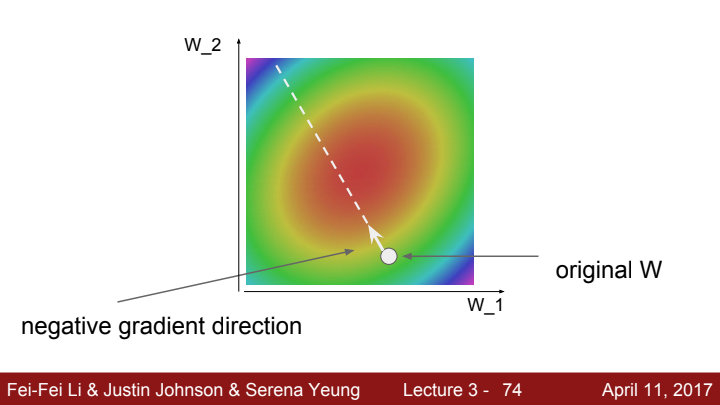
한 지점에서 Gradient Descent 한 step을 하는 과정을 보여주는 그림입니다. 저 흰 점에서 구한 negative한 gradient 값이 흰 점선과 같고, 우리는 우리가 정해준 learning rate만큼 보폭을 이동한 후 새로운 점에서 또 다시 새로운 gradient를 구한 후 새 방향으로 보폭을 또 옮기고 이를 우리가 정해준 학습 횟수(이를 epoch라고 합니다)만큼 반복해 줄 것입니다.
Stochastic Gradient Descent(SGD)

GD는 가중치를 optimization하기 매우 좋은 방법이지만 단점이 존재합니다. 바로 dataset의 크기가 방대할수록 한 번 가중치를 update하는 과정의 비용이 비싸진다는 점인데요. 컴퓨팅 파워뿐만 아니라 한 번 학습하는 데 걸리는 시간또한 막대하게 들어가겠죠?
이러한 문제를 해결하기 위해, 데이터셋을 여러 개의 작은 mini batch로 나누어 각각의 mini batch를 가지고 학습시킨 뒤 gradient descent를 하는 방법을 SGD라고 합니다.
RNN을 공부하다 보면 이와 비슷한 개념인 truncated BPTT라는 backpropagation 과정에 대해 배우게 됩니다. cs231n 강의에도 RNN에 대한 내용이 포함되어 있으니 자세한 내용은 그 때에 가서 다시 설명해 보겠습니다.
저는 이 SGD와 truncated BPTT를 배우며 무슨 생각이 들었냐면, 'Greedy Algorithm과 매우 닮아있다'라는 생각이 들었습니다. 무슨 뜻이냐고요?
그리디 알고리즘은 하나의 큰 문제를 여러 작은 부분 문제로 쪼개 각 부분 문제에 대한 최적값을 가지고 전체 문제의 최적값을 구하는 알고리즘입니다. 간단하고 실용적인 알고리즘이지만, 부분 문제에서의 최적해의 집합을 통해 구한 값이 전체 문제에서의 최적해라는 보장이 없다는 단점이 존재합니다. 무슨 뜻이냐고요? 이 글은 알고리즘 강의가 아니기 때문에 이해가 잘 되지 않으시면 그냥 글쓴이의 헛소리라 생각하고 무시하셔도 좋을 것 같습니다...
SGD는 각 미니배치에서 구한 gradient 방향으로 가중치를 미니배치의 개수만큼 업데이트시켜 한 epoch에서의 가중치 업데이트를 완료합니다. 이 과정에서 각 미니배치에서의 최적의 방향으로 가중치를 업데이트 시켰다 한들, 전체 데이터셋의 관점에서 이 SGD를 가지고 epoch 한 번을 돌려 업데이트 된 가중치가 GD를 통해 한 epoch동안 업데이트 된 가중치보다 나쁘면 나빴지 더 좋을 일은 없다는 의미입니다.
물론 수렴 속도가 GD보다 느릴 수는 있지만, 수렴의 효율성은 SGD가 더 뛰어나다고 볼 수 있습니다. 최적점 근처에 빠르게 도달할 수 있기 때문이죠. 수렴 지점의 정확한 값이 0.1234567이라고 쳐봅시다. GD를 통해 결국에 이 값에 SGD보다 accurate하게 결국 도달을 하게 되더라도, SGD를 사용한다면 저 값의 근접 구간에 훨씬 빠르게 도달할 수 있을지도 모릅니다. 0.123정도로 말이죠!
부분 문제에서의 최적해의 조합이 오히려 그냥 GD를 통해 구한 최적해보다 더 나은 결과를 보일 수도 있습니다. GD에서 발생할 수 있는 특정 데이터셋에 대한 과적합, 초기값 설정에 의해 local 최적값에 도달할 경우의 수 등을 고려한다면 말이죠.
또한, 미니배치 한 번에 대한 업데이트는 짧겠지만 결국 같은 수의 데이터셋을 가지고 epoch을 돌리기 때문에 전체 업데이트 시간은 크게 차이나지 않을 것이고 또한 수렴 속도는 오히려 느릴 수도 있습니다.
그럼에도 SGD를 사용하는 이유는 무엇이냐! 제 생각에는 학습 한 번에 사용되는 데이터의 크기가 상대적으로 작기 때문에 컴퓨터가 학습을 하는 데 드는 부담이 적다는 것이 가장 큰 이유일 듯 싶고(팔굽혀펴기 100번을 해야한다고 했을 때 1개씩 100번 나눠서 하는 게 100번씩 한 세트 하는 것보다 당연히 부담이 적겠죠?),
또한 만일의 경우 학습이 중간에 중단되는 참사가 발생하더라도 한 epoch의 중간중간 학습 상황을 저장해주었다면 끊긴 부분부터 transfer learning을 해주기 용이하다는 장점이 있을 것입니다.
(서류 작업으로 치면 한 줄 한 줄 적을때마다 ctrl+s로 문서 저장을 계속 해준다고 보면 될 거 같습니다. 귀찮지만 만일 정전으로 컴퓨터가 중간에 꺼지는 대참사가 발생해도, 한 장씩 쓰고 저장하는 옆 자리 신입사원보다는 큰 피해를 방지할 수 있는...)
SGD는 앞서 설명드린 부분 외에도 여러 단점들을 가지고 있어 이를 보완하기 위한 또 다른 Optimization 방법들이 여럿 존재합니다. 이에 대해서는 차후 강의에서 소개해드리도록 하겠습니다.
Aside: Image Features
추가적으로, 딥러닝이 본격적으로 사용되기 전 사람들은 어떻게 이미지로부터 feature를 추출했는지에 대한 방법들을 소개하고 있습니다.
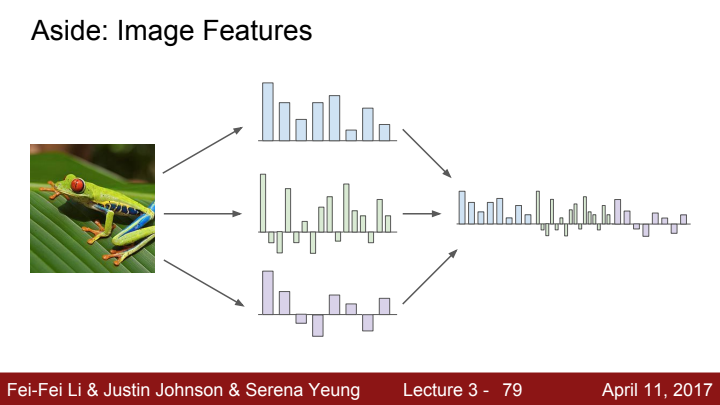
Raw data 자체를 가지고 linear classifier를 훈련시키는 것보단, 이미지에서 다양한 quantity들을 추출 후 cancatenate시킨 특징 벡터를 linear classifier에 태워주었다고 합니다. Raw data 자체를 활용하지 않는 이유는 multi modality 등의 문제 때문이라고 하네요(무슨 의미일까요...).
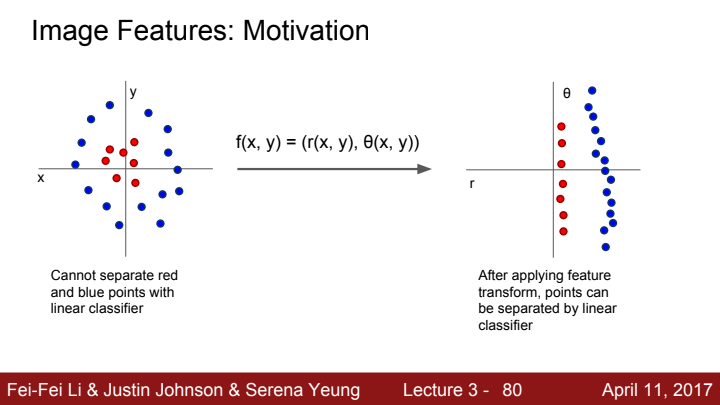
다음과 같이 직선으로 분류가 어려운 분포를 가지고 있는 데이터의 경우, 극좌표 변환 등과 같은 feature transform을 통해 직선으로 구분이 가능하도록 데이터 분포를 변경시켜주면 linear classifier를 가지고 feature를 추출할 수 있을 것입니다.
이 feature transform을 활용하는 방법론으로는 이미지의 색깔 분포를 가지고 histogram으로 표현하는 Color histogram, 각 픽셀의 orientation을 파악하는 HoG(Histogram of Oriented Gradient), 사진을 랜덤하게 patch들을 추출한 뒤 visual word를 할당한 후 patch들을 cluster하여 visual word들의 codebook형태를 만든 뒤 각 visual word의 빈도를 조사하여 classification하는 Bag of Words등이 존재합니다.
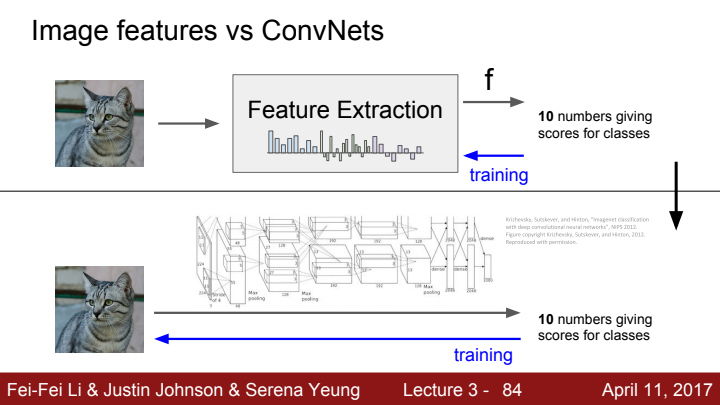
위의 사진에서처럼 Image feature를 활용하여 classification을 하는 방법의 경우, 알고리즘을 활용해 feature를 extract하고 그것을 linear classifier에 태워 결과를 도출합니다. training을 통해 학습될 수 있는 것은 linear classifier 뿐입니다.
반면에 Convolution Neural Network의 경우, Convolution layer로 구성된 Feature extracter와 FC layer로 구성된 linear classifier 모두 학습이 가능합니다. 고정된 하나의 알고리즘을 가지고 Feature extraction을 수행하는 Image feature에 비해 ConvNets은 Feature extraction마저도 학습을 할 수 있어 해당 과정에 대한 정확도가 더욱 상승하고 유연성 또한 가지게 되겠죠?
다음 강의에서는 이 머신러닝/딥러닝 모델을 학습시키는 방법인 backpropagation과 Neural Network에 대해 자세히 다뤄보도록 하겠습니다.
