1. O(nlogn) 정렬

지난 시간에 배웠던 정렬 알고리즘들은 O(n^2) 시간인 반해, 앞으로 소개할 정렬 알고리즘은 O(nlogn)이다.
참고로 O(nlogn)과 O(n^2)이 별로 차이가 안나보여도 엄청난 차이가 있다.
직접 종이를 가져와서 N = 10^5을 넣어보고 값의 차이를 보면 체감할 수 있다.

이전에 배웠던 정렬 알고리즘들은 왜 O(n^2)이 걸렸을까??
그건 아주 단순하다.

버블 정렬, 선택 정렬, 삽입 정렬 모두 비교 과정에서 자신의 옆 자리와 값을 비교하기 때문이다.
그렇기 때문에 N개의 원소들을 N-1개들 끼리 비교를 하다보니 O(N^2) 시간이 걸리는 것이다.

그렇다면 O(nlogn)은 어떻게 가능한 걸까??
아주 단순하다. 그럼 옆에 있는 원소들끼리 비교를 안하면 되지~

그걸 누가 몰라?

그렇다 이제부터 배울 정렬 알고리즘은 양 옆의 원소들끼리 값을 비교하지 않는다.
대신 아주 신박한 기법을 도입하는데 그것이 바로

분할 정복 이다.

분할 정복?? 'divide and conquer' 라고도 하는데, 정말 어려운 개념이지만 우리는 간단하게 생각하도록 하겠다. 어떤 문제가 있다면, 문제를 쪼개서 해결한 다음, 이들을 합쳐 해결하자는 것이다.

이것이 무슨 의미가 있고? O(nlogn)과 무슨 상관인가?? 한다면, 분할 정복이 잘 적용된 정렬 알고리즘인 병합 정렬을 알아가면서 이해해보도록 하자

2. 병합 정렬(merge sort)

합병 정렬, 병합 정렬 이라고 한다.

병합 정렬의 핵심

병합 정렬의 핵심은 앞서 소개한 분할 정복이다.
병합 정렬에서 사용된 분할 정복은 다음과 같다.

분할 : 배열이 있다면, 반으로 쪼개자
정복 : 쪼개진 배열을 합치자, 단 합칠 때는 서로 정렬을 하도록 하자

이렇게 분할된 배열을 정복(합쳐서 정렬)하면 정렬이 완성될 것이다.

역시 글로 보면 이해가 안된다.
그림으로 보도록 하자

다음과 같은 배열이 있다고 하자, 여기서 우리는 병합 정렬로 해당 배열을 정렬하려고 한다.
병합 정렬의 핵심이 무엇이라고??
분할 정복이다. 분할 정복이므로 분할이 먼저이다.
분할 : 배열이 있다면 반으로 쪼개자는 것이다.

이렇게 반으로 갈아버리면 된다.
그럼 언제까지 반으로 갈라버리는가??
원소가 더 이상 쪼개지지 않을 때까지 갈라버리면 된다

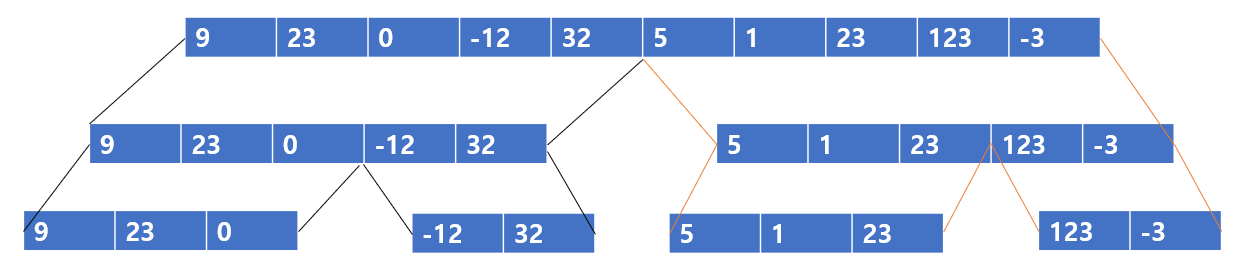
더 분할하자

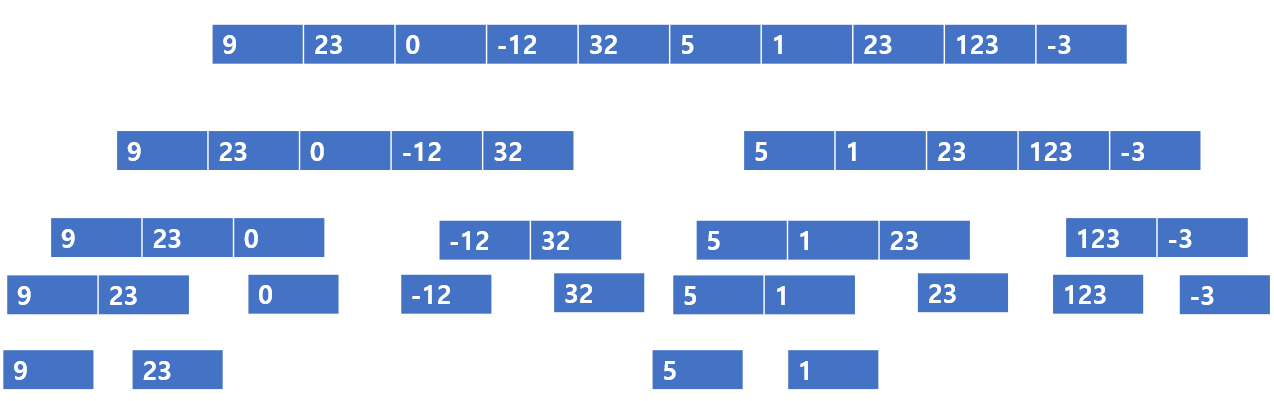
이것이 분할 연산의 마지막 모습이다. 각 배열에 원소 한 개씩 밖에 존재하지않아 더 이상 갈라질 수 없다. 분할 연산이 끝났으니 이제 무엇이다???
정ㅋ벅ㅋ이다.
정복이 의미하는 바는 여러 의미가 있는데, 보통 문제를 해결하는 로직이라는 의미이다. 따라서 우리는 정렬을 하고 싶어하므로, 정복은 정렬을 의미한다.

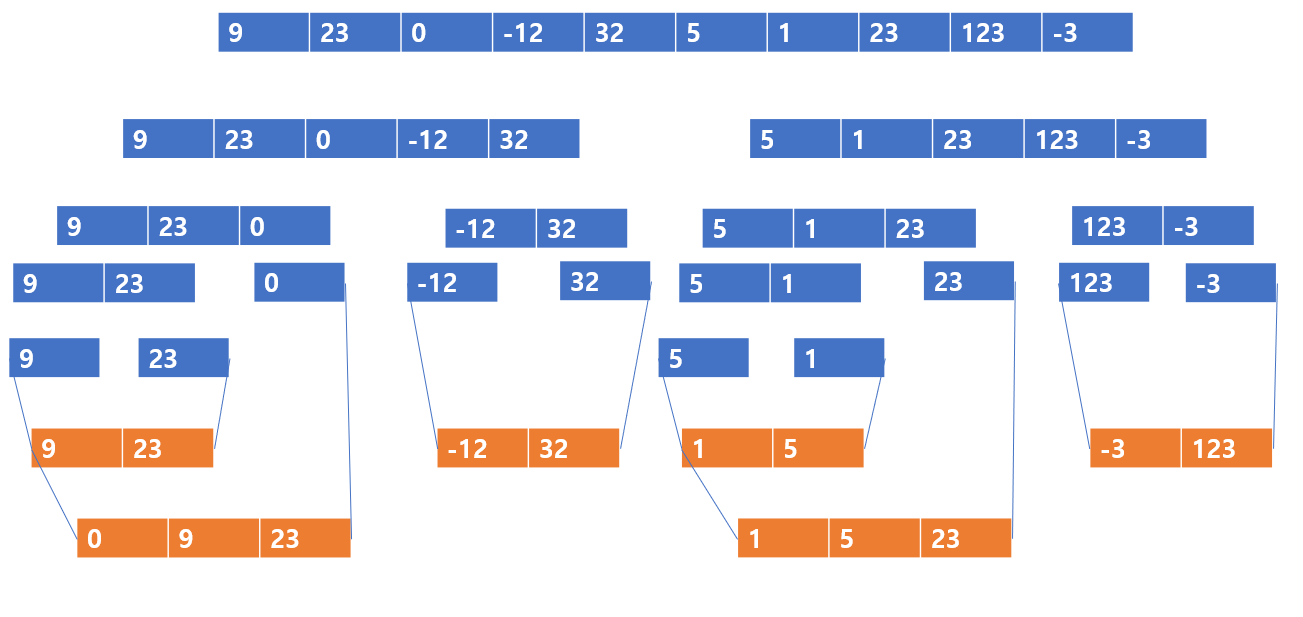
바로 이렇게 말이다. 주황색으로 표시한 부분을 보자
왼쪽부터 보면 [9,23] 으로 된 배열과 [0]으로 된 배열을 병합 시킨다.
병합에서 마무리 되는 것이 아니라, 크기에 따라 정렬을 시켰다.
그 다음 [-12] 와 [32] 역시도 병합시키고 정렬시켰다.
[1,5] 와 [23] 역시도 병학하고 정렬하여 [1,5,23]이 나왔다.

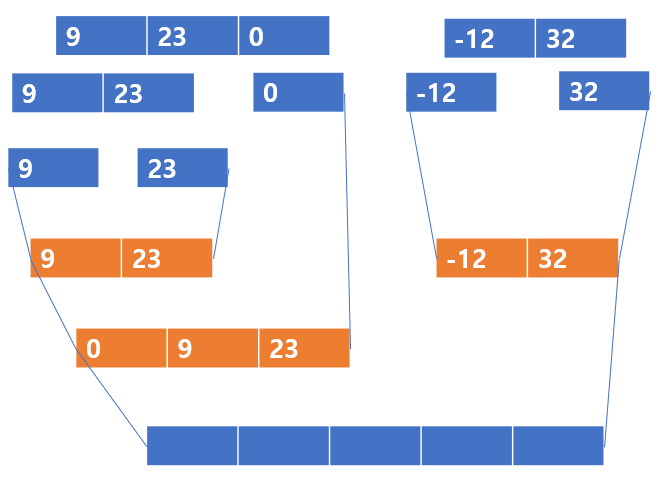
사실 병합은 어렵지 않다.
위의 예제의 경우 [0,9,23]과 [-12,23]을 병합한다면 배열 크기 5짜리 공간을 따로 만들어주고 값을 넣어주면 된다. 그런데, 어떻게 정렬을 하냐가 중요하다.

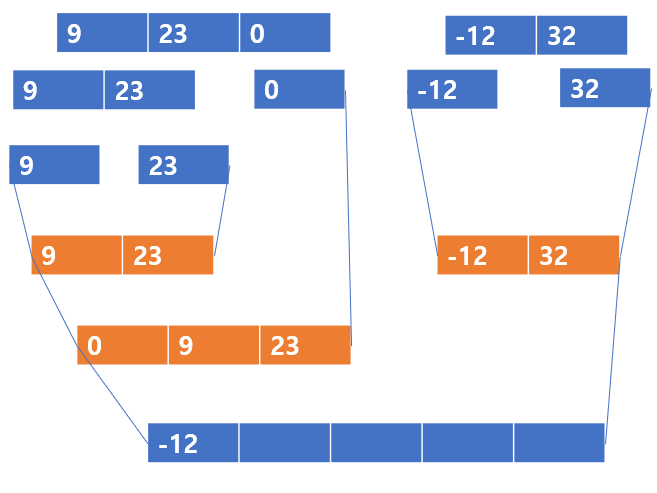
다음은 정렬의 예이다.
[0,9,23] 과 [-12,23] 을 보자, 이 두 배열 역시 이전의 정복(병합 후 정렬) 연산으로 정렬이 된 상태이다. 그럼 이 사실을 이용해보자
정렬이 된 배열에서(오름 차순이라고 하자) 맨 처음 값은 해당 배열에서 가장 작은 값일 것이다.
그렇다면, 두 배열을 병합한 배열에서 맨 처음에 나오는 값은 두 배열의 값 중 가장 작은 값 중에 작은 값을 것이다. 즉, [0,9,23] 에서는 0 이고, [-12,23]에서는 -12 일 것이다.

그럼 이 둘을 비교하면 병합된 배열에서 가장 작은 값이 될 것이다.
0 > -12 이므로, -12가 가장 작은 값이다.
따라서 병합된 배열의 가장 첫번재 값은 -12가 될 것이고, [-12, 23]에서 -12를 빼자
그럼 병합된 배열의 두 번째 값은 무엇일까?
위의 사실을 적용해서 생각해보자

어찌됐거나 [0,9,23] , [23] 에서 하나의 값인데, 두 배열 모두 정렬된 값이니까 또 맨 앞의 값이 병합된 배열의 두 번째 값이 될 수 밖에 없다. 병합된 배열의 두 번째 값은 두 번째로 가장 작은 값이기 때문이다.

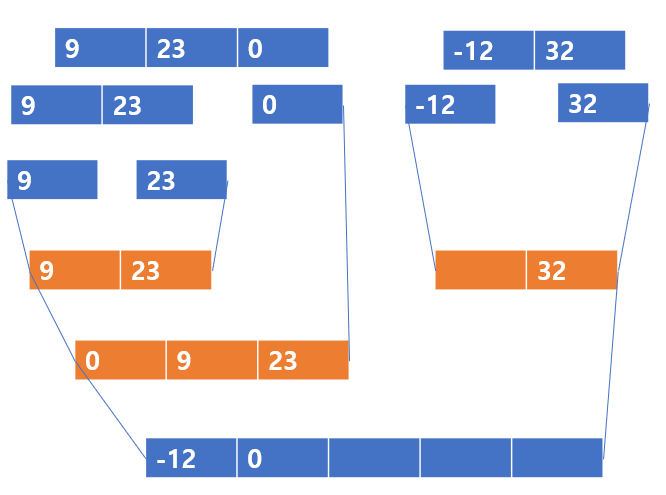
따라서 [0,9,23] 과 [32] 의 맨 앞 값을 비교하면 0 < 32 이므로 0 이 병합된 배열의 두 번째 값이 된다.
[-12, 0] 이 된다.

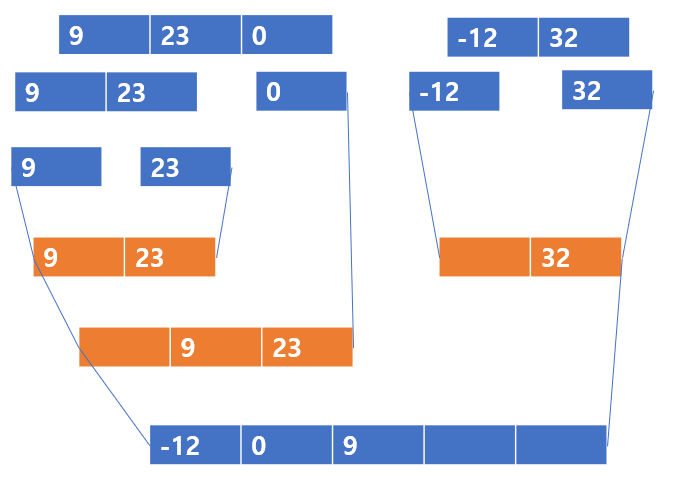
이렇게 세번째 값까지 비교해주면 9 < 32 이므로 9가 들어가고

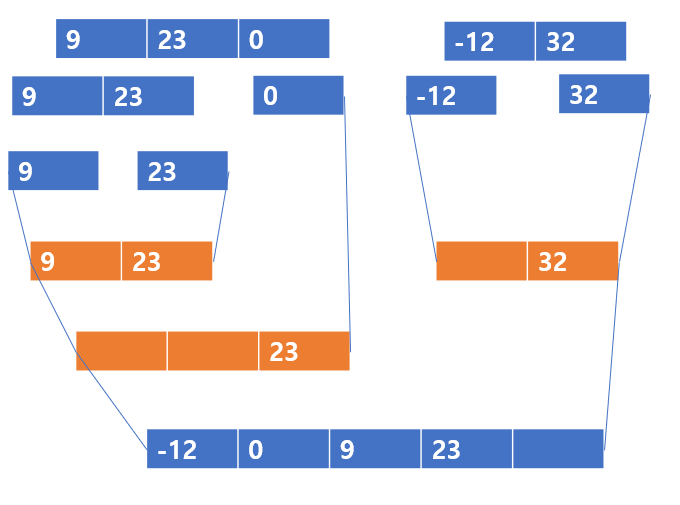
23 < 32 이므로 23이 들어가고

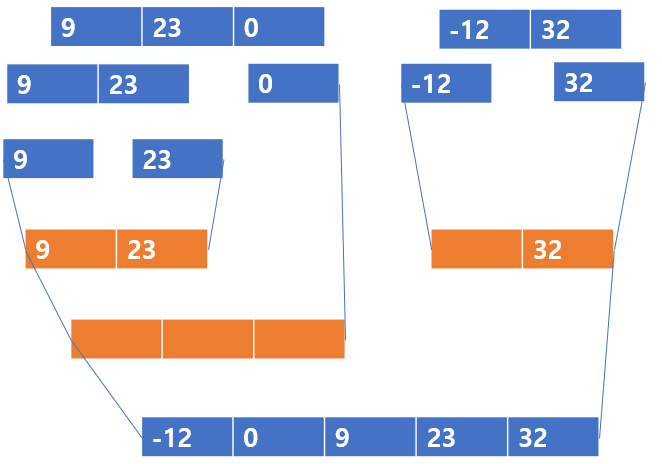
마지막으로 남은 값은 32를 넣어주면 끝이다.

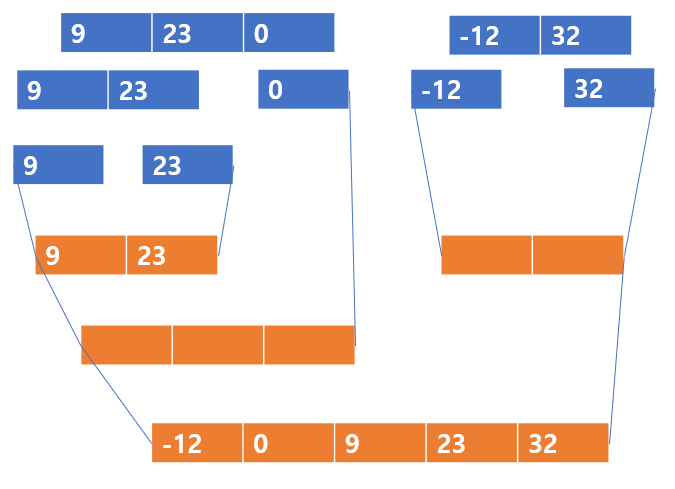
짜잔, 분할된 배열을 병합하여 정렬하는 정복 과정이 끝난 것이다.
이렇게 정렬된 배열을 얻고, 정렬된 배열끼리 또 정복 과정을 거치는 것이다.

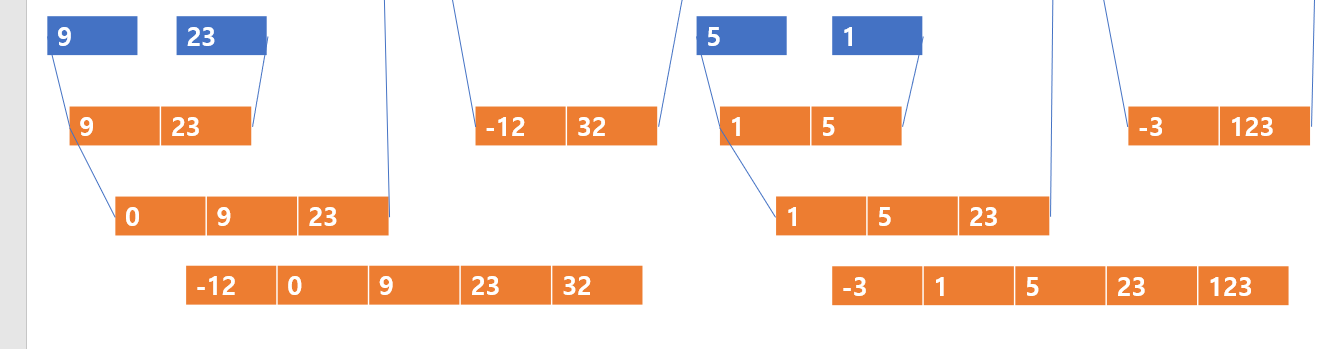
위의 전체 과정 그림을 보면 오른쪽 부분도 [1,5, 23] 과 [-3,123] 을 정복하여 [-3, 1, 5, 23, 123]을 얻었다. 이제 마지막으로 두 배열을 정복(병합하고 정렬)하도록 하자

이제 분할된 배열들이 정복 단계를 거쳐 마지막 단계의 정복에 대한 예를 보여주겠다.
[-12,0,9,23,32] 와 [-3,1,5,23,123] 두 개의 배열을 정복(합병 후 정렬)하도록 하자
가장 먼저 -12와 -3을 비교한다. -12이가 더 작으므로 병합된 배열에 들어간다.

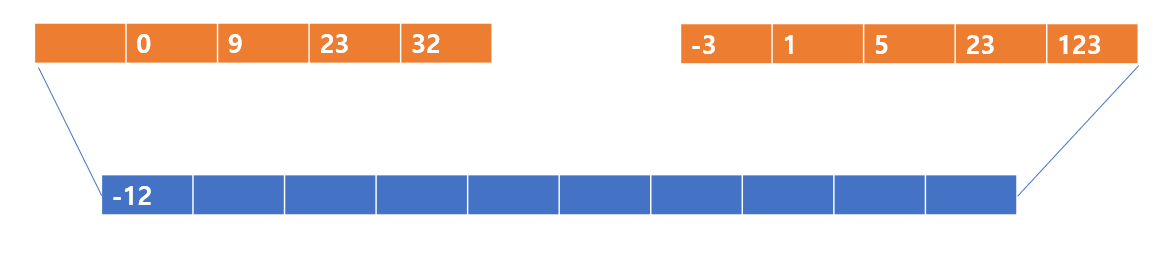
-12가 들어갔다. 그 다음은 0과 -3을 비교한다. -3이 들어가게 된다.

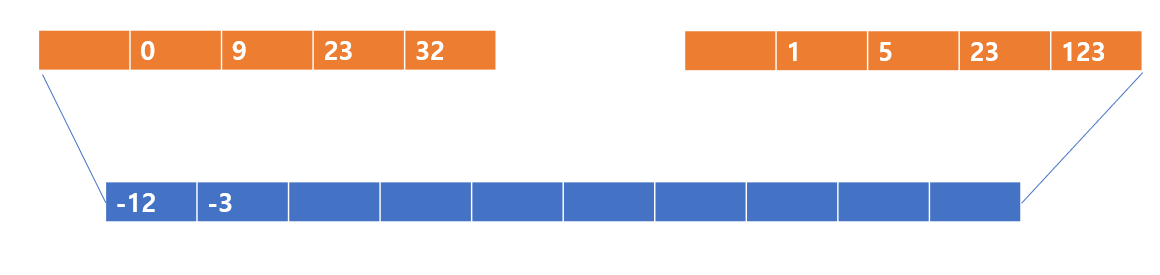
-3이 들어간 모습이다. 이 다음에는 0과 1을 비교하고 0이 들어간다.
그 다음은 9과 1을 비교하게 될 것이다.

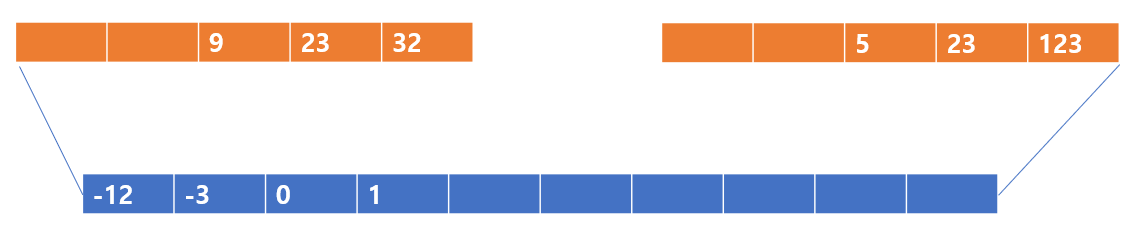
다음과 같은 모습이 될 것이다.
이제 9와 5를 비교하면 5가 들어갈 것이다.

여자저차 어기야 궁더러러 하다보면 이런 배열 모습이 된다.
즉, 오름차순으로 정렬된 모습이 된다.

이렇게 병합 정렬은 두 가지 연산
1. 분할
2. 정복(병합 후 정렬)

이라는 방법으로 정렬을 마칠 수 있는 것이다.
이것이 분할 정복인 것이다.

더 간단하게 말해서, 배열을 쪼개서 정렬한 다음 합쳐서 정렬시키면 정렬된 배열이 만들어 질 것이다. 라는 것이다.
이들은 서로 양 옆에 있는 원소들을 비교하여 자리를 바꾸는 것이 아닌, 분할된 배열을 기준으로 정렬을 시도한다. 따라서 O(nlogn)이 가능한 것이다.

오잉? 조금 의아할 것이다. 어떻게 O(nlogn)이라는 수가 나왔는 지 말이다.
일단, 우리는 분할을 해야한다. 배열 사이즈가 N이라면 N이라는 수를 N/2로 만들고, N/2를 N/4로 만들어야 한다. 계속해서 사이즈를 2로 나누는 것이다. 그리하여 원소가 하나 밖에 남지 않을 때까지 만드는 것이다. 또한, 여기서 나누어진 두 배열에 대한 비교 연산 시간이 필요하다. 이는 최대 N 번이 걸리게 된다.

그렇다면 시간 복잡도는 다음과 같다.
T(N) = 2T(N/2) + N --- 1번 식
여기서 N = N/2 를 넣어보자
T(N/2) = 2(T/4) + N/2 --- 2번 식

2번 식을 1 번식에 넣어보자
T(N) = 22T(N/4) + 2*(N/2) + N

정리하면
T(N) = 4*T(N/4) + 2N
이 된다.

따라서, 다음 N/4를 넣고, 그 다음 N/8을 넣고, 이 과정을 K번 반복하면
T(N) = (2^k)*T(N/(2^K)) + KN 이 된다.

여기서 N = (2^K)를 대입해보자, (참고로 왼쪽 식을 통해서 K = logN 임을 알 수 있다)
T(N) = N*T(1) + NlogN 이 된다.
T(N) = N + NlogN 이 되는 것이다
N보다 NlogN 이 더 크므로 대충 시간 복잡도는 O(NlogN)이 되는 것이다.

더 쉽게 이해하자면 반으로 나누어 원소가 1 개 밖에 안남게되면 이는 연산을 logN번 반복하게 된다. 이는 트리의 높이와 같기 때문이다.
그렇다면 남은 건 정복(병합 후 정렬)과정인데 이는 한 번에 N시간이 걸리지만 총 logN번 해야한다. 왜냐하면 트리의 높이와 같기 때문이다. 따라서 NlogN이 걸리는 것이다.

코드

#include <iostream>

using namespace std;

int n = 10;
int data[] = {9,23,0,-12,32,5,1,23,123,-3};

void merge(int left, int right){
	int mid = (left+ right)/2;
	int i = left;
	int j = mid+1;
	int c = left;
	int temp[10] = {0,};
	while(i <= mid && j <= right){
		if(data[i] <= data[j]){
			temp[c++] = data[i];
			i++;
		}
		else if(data[i] > data[j]){
			temp[c++] = data[j];
			j++;
		}
	}
	while(i <= mid) temp[c++] = data[i++];
	while(j <= right) temp[c++] = data[j++];
	for(int i = left; i <= right; i++){
		data[i] = temp[i];
	}
	
}

void mergeSort(int left, int right){
	if(left != right){
		int mid = (left + right)/2;
		mergeSort(left,mid);
		mergeSort(mid+1,right);
		merge(left,right);
	}
}

int main(){
	mergeSort(0,n-1);
	for(int i = 0; i < n ;i++){
		cout << data[i] << ' ';
	}
}

설명하면 다음과 같다.
분할과 정복 두 가지 연산으로 나뉜다고 했다.
여기에 집중해보자

void mergeSort(int left, int right){
	if(left != right){
		int mid = (left + right)/2;
		mergeSort(left,mid);
		mergeSort(mid+1,right);
		merge(left,right);
	}
}

해당 함수는 분할 부분이다.
mid를 중심으로 left와 right를 나누고 분할이 끝난 뒤에 merge를 시도한다.

void merge(int left, int right){
	int mid = (left+ right)/2;
	int i = left;
	int j = mid+1;
	int c = left;
	int temp[10] = {0,};
	while(i <= mid && j <= right){
		if(data[i] <= data[j]){
			temp[c++] = data[i];
			i++;
		}
		else if(data[i] > data[j]){
			temp[c++] = data[j];
			j++;
		}
	}
	while(i <= mid) temp[c++] = data[i++];
	while(j <= right) temp[c++] = data[j++];
	for(int i = left; i <= right; i++){
		data[i] = temp[i];
	}
	
}

다음은 정복(병합 후 정렬) 부분이다.
총 3개의 인덱스 변수가 필요한데, 왼쪽 배열의 맨 왼쪽 값과 오른쪽 배열의 맨 왼쪽 값을 비교하기 위한 인덱스 i, j와 이들을 병합한 배열의 인덱스(즉, 값이 들어갈 자리)를 나타내는 c변수이다.

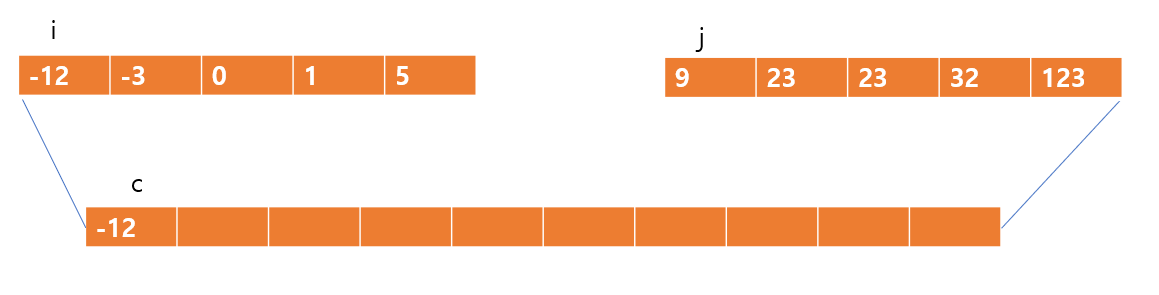
(왼쪽과 오른쪽 배열, 그리고 합병된 배열 위에 있는 인덱스에 유의하자)
-12와 9를 비교하게 되고, -12는 c가 가리키는 위치에 값을 넣는다. -12는 왼쪽 배열에서 사리지므로 i는 한 자리 옮기게 되고, c역시 한 자리 옮기게 된다. 반면 j는 9를 넣은게 아니므로 가만히 있는다.

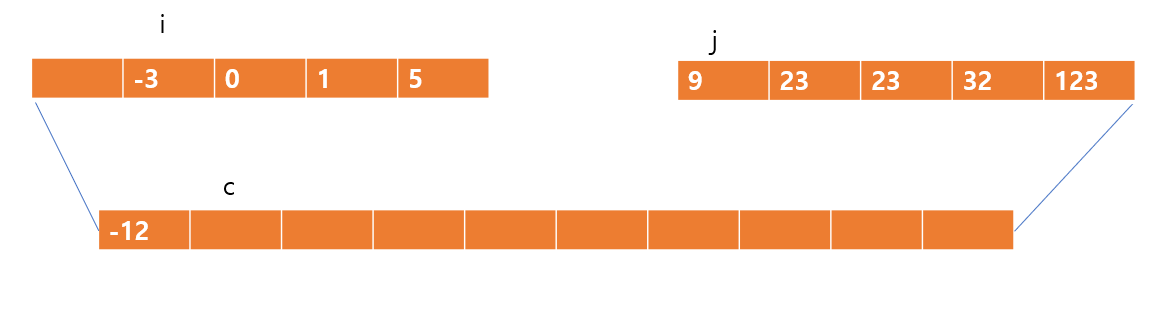
이렇게 옮겨진다는 것이다. 그러면 나머지 연산에 대해서 손으로 써보면 i,j,c의 움직임을 알 수 있다.

정리하자면
i : 왼쪽 배열에서 값을 비교하기 위한 인덱스
j : 오른쪽 배열에서 값을 비교하기 위한 인덱스
c : data[i], data[j] 중 더 작은 값이 병합한 배열에서 들어갈 위치를 나타내는 인덱스 변수
이다.

while(i <= mid && j <= right){
		if(data[i] <= data[j]){
			temp[c++] = data[i];
			i++;
		}
		else if(data[i] > data[j]){
			temp[c++] = data[j];
			j++;
		}
	}
	while(i <= mid) temp[c++] = data[i++];
	while(j <= right) temp[c++] = data[j++];

while() 문으로 data[i]와 data[j]를 비교한다.
while( i <= mid)와 while( j <= right)는 만약 왼쪽 배열이나 오른쪽 배열 중 한 배열이 텅 비게되었을 때 나머지 배열에서 남은 값을 모두 가져오는 연산이다.

가령 이런 것이다. 왼쪽 배열은 텅텅인데, 오른족 배열은 값이 남아있다.
따라서 이 남은 값을 병합한 배열에 넣어주는 것이다.
while( j <= right) j++; 이 된다.

for(int i = left; i <= right; i++){
		data[i] = temp[i];
	}

은 병합한 배열의 값을 원래 배열의 자리에 넣어주는 연산이다.

위 코드를 보아서 딱 느낌이 드는 것이 있을 것이다.
병합 정렬을 쓰려면 원래 배열의 크기 N 만큼의 크기를 가진 또 다른 배열이 필요하다.
이는 메모리 낭비가 매우 심하다는 이야기이고, 이것이 병합 정렬이 가진 최악의 단점이다.
그러나, 전반적으로 우수한 시간복잡도와 구현하기 편하고 이해하기 쉽다는 장점을 가져, 만약 O(nlogn) 정렬 알고리즘을 손코딩하라고 하면 병합 알고리즘을 짜기를 권장한다.

다음은 같은 O(nlogn) 시간인 쿽정렬에 대해서 알아보도록 하자

(+ 2024/06/20 Python code 추가
백준 2751번 문제에 대한 merge sort 정답이다.

https://www.acmicpc.net/problem/2751

import sys
inputs = sys.stdin.readline
print = sys.stdout.write

n = int(inputs())
nums = []
temp = [0] * n

for i in range(n):
    v = int(inputs())
    nums.append(v)

def merge(s, e):
    if s == e:
        return

    mid = (s + e) // 2
    i = s
    j = mid + 1
    c = s

    while i <= mid and j <= e:
        if nums[i] < nums[j]:
            temp[c] = nums[i]
            c += 1
            i += 1
        else:
            temp[c] = nums[j]
            c += 1
            j += 1

    while i <= mid:
        temp[c] = nums[i]
        c += 1
        i += 1
    while j <= e:
        temp[c] = nums[j]
        c += 1
        j += 1

    for k in range(s, e+1):
        nums[k] = temp[k]

def divide(s, e):
    if s < e:
        mid = (s + e) // 2
        divide(s, mid)
        divide(mid + 1, e)
        merge(s,e)

divide(0, n-1)

for i in range(n):
    print(str(nums[i]) + '\n')

전반적으로 c++구현하고 다를 바는 없다.