알고리즘 6일차 - O(n) 정렬, 계수 정렬

왜!! 정렬 알고리즘은 끝이 없는 것인가!!

하늘은 왜! O(N) 정렬까지 낳으신 것인가!!
라고 해도 어쩔 수 없다. 그러나 이전에 맛본 O(nlogn)보다 훨씬 더 쉽고 간단하다.

이전에 O(n^2) 알고리즘은 자신의 옆에 수와 비교해야하므로 n^2의 한계를 벗어나지 못한다고 하였다. O(nlogn) 알고리즘은 자신의 옆에 수 말고, 건너건너 수와 비교하여 하나 당 logn시간의 비교를 하여 O(nlogn)시간을 완성할 수 있었다. 그러나 이는 어떤 수와 비교를 하여 정렬을 한다면 결국 O(nlogn)시간을 벗어날 수 없다는 한계에 봉착한다는 것이다.

그래서 O(n) 정렬 알고리즘은 비교를 하지 않는다!! 뭔 개소리인가 싶은데 배워보면 이해가 된다.

O(n) 정렬 알고리즘은 두 가지가 있는데, 하나는 계수 정렬(counting sort), 하나는 기수 정렬(radix sort)가 있다. 둘 다 굉장히 단순하고 직관적인데, 어딘가 배우지 않았어도 구현해보았을 만도 한다. 그런적 없다면 같이 배우면 된다.

O(n) 정렬 알고리즘에는 제한 조건이 있는데, 바로 양수만 가능하다는 것과 숫자의 범위가 엄청 크지 않아야 한다는 단점이다. 이러한 이유 때문에 O(n) 정렬 알고리즘임에도 범용적으로 쓰이지 못하는 것이다. 그래서, 이번 O(n) 정렬 알고리즘은 가볍게 배우고 넘어가도 좋다.

1. 계수 정렬(counting sort)

기본적으로 다음의 제약 사항을 갖는다.

1. 데이터(값)은 양수여야 한다.
2. 값의 범위가 너무 크지 않아야 한다.(메모리 사이즈를 넘어서는 안된다.)

1과 2 제약사항이 존재하는 가장 큰 이유는, 우리가 배열의 인덱스를 이용하여 데이터를 저장할 것이기 때문이다. 따라서, 배열의 인덱스는 양수만 존재하고, 값이 너무 커지면 메모리 영역을 너무 많이 할당해버려 문제가 생기므로 위의 두 조건이 붙게되는 것이다. 이 제약 사항은 계수 정렬 뿐만 아니라, 다음 시간에 배우는 기수 정렬(radix sort) 역시 마찬가지이다.

2. 계수 정렬의 원리

각설하고, 계수 정렬의 원리에 대해 알아보자.

계수 정렬의 아이디어는 굉장히 단순하다.
[3,4,1,2,4,6,1]

이라는 배열이 있다고 하자
우리는 O(n^2), O(nlogn) 정렬 알고리즘으로 이 배열을 정렬할 수도 있지만, O(n)안에 해결할 수도 있다.

어떻게?? 해당 배열에서 각 숫자가 몇 개 나오는 지 세어보도록 하자

1 : 2개
2 : 1개
3 : 1개
4 : 2개
6 : 1개

그렇다면, 1부터 6까지 갯수대로 나열해보자

[1,1,2,3,4,4,6]

아주 자연스럽게 정렬이 되었다.
이게 끝이다 ㅎㅎㅎ;;

시시해서 죽고싶어졌다....

계수 정렬은 정말 이게 끝이다. 각 숫자가 몇 번 나오는 지를 알고, 이를 앞 순서대로 차례대로 써주기만 하면 정렬이 된 것이다.

더 자세히 원리를 정리해두고 예제를 보자,

1. 계수 정렬(counting sort)는 정렬되지 않은 배열의 수들이 몇 번 나왔는지 적어둔다.
2. 몇 번 나왔는 지 기록한 배열을 count 배열이라 하자, count 배열을 앞부터 순회하여, 자신이 정렬된 배열에서 몇 번째에 나와야 하는 지 기록하도록 하자.
3. 정렬된 배열에서 자신이 몇 번째에 나와야하는 지 기록한 배열을 sum 배열이라 하자, sum 배열의 맨 마지막 값부터 순회하여, 정렬 배열에 값을 써둔다.
4. 값을 쓸 때, count배열과 sum배열의 값을 하나씩 줄이고 0 될 때 까지 반복한다.

뭔가 복잡해보이지만 아래의 예제를 보고 다시보면 간단하다.

다음의 정렬되지않은 배열이 있다고 하자, 이걸 계수 정렬을 하도록 하자
먼저 count 배열, 즉, 각 숫자가 몇 번 나왔는 지를 세어보도록 하자

0 : 1개
1 : 3개
3 : 2개
23 : 2개
32 : 1개
123 : 1개

다음과 같이 count 배열이 나오게 된다. 그럼 해당, count 배열을 통해 sum 배열을 만들어주자, sum 배열은 내 앞에 숫자가 몇 개 있느냐를 세어주는 것이다.

0 : 1개
1 : 4개
3 : 6개
23 : 8개
32 : 9개
123 : 10개

즉 , 현재 숫자 앞의 숫자들의 개수 + 현재 숫자 개수를 저장해주는 것이다.

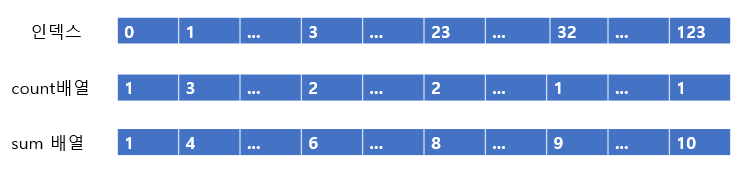
정리하면 다음과 같다.
왜 sum 배열을 만들어주는가? sum배열은 현재 숫자 앞의 개수 + 현재 숫자이다.
그 말은 현재 숫자가 정렬된 배열에 어디에 위치해야하는 지 표시한 것과도 같다. 즉 0은 1개이므로 1번 인덱스에 위치하고, 1은 3개이지만 앞에 0이 한 개 있으므로 3이다. 따라서 2 ,3, 4 번 인덱스에 1 1 1 을 위치시키면 된다는 것이다.

이 과정을 아래에 계속 반복하여 예제로 보여주겠다.

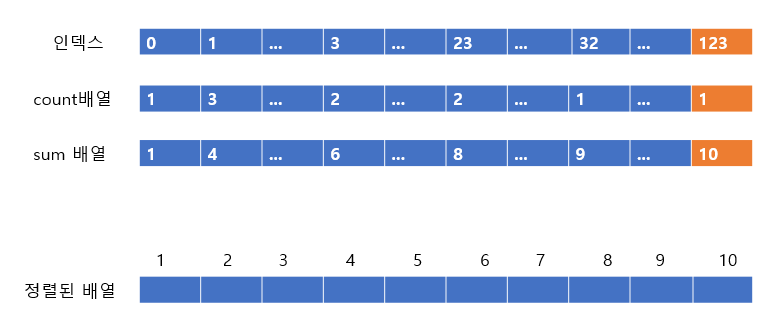
이후에 정렬 배열을 정리하며 할 이야기인데 배열에서는 stable과 unstable이 있다. stable은 정렬이 안된 배열에서 같은 숫자가 있을 때, 정렬할 때도 이 순서가 지켜짐을 의미한다.
[4, 1 , 2, 1] 이 있다면

1이 두번 나오는데, 맨 처음에 나오는 1을 ㄱ1, 두번째에 나오는 1을 ㄴ1이라고 한다.
정렬 알고리즘을 돌리면
stable한 경우 : [ㄱ1,ㄴ1,2,4]
unstable한 경우 : [ㄴ1,ㄱ1,2,4]

이렇게 된다. 즉, 정렬하여 같은 숫자들의 위치가 바뀌냐 안바뀌냐에 따라 결정되는 것이다. 계수 정렬(counting sort)는 stable함을 유지하기위해 맨 뒤의 수부터 값을 채워준다. 만약 unstable해도 상관없다면 앞에서부터 채워도 문제가 될 것은 없다.

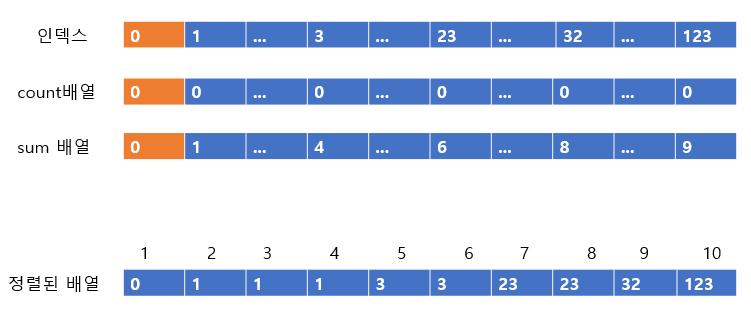
위의 사진에서 주황색으로 표시한 부분을 보도록 하자, 주황색 부분에서 인덱스 123은 count 배열에서 1이다. 즉 1개 있다는 거싱고, sum 배열에서는 10이다. 이는 앞에 9개의 값이 있기 때문에 자신이 있어야할 자리는 10번째라는 것이다. 따라서 아래에 정렬된 배열에 123을 10번째 인덱스에 넣어주고 count배열과 sum배열의 값을 줄여준다.

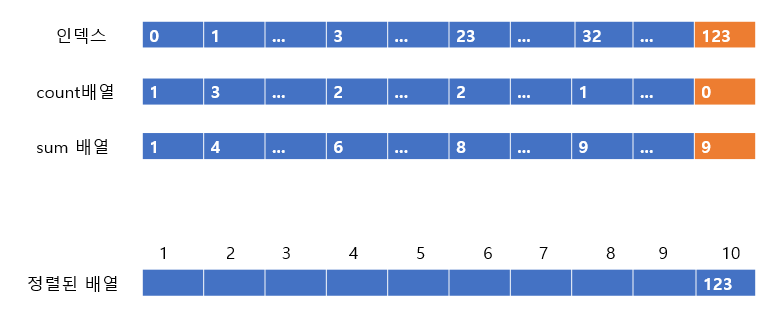
이렇게 된다.

다음 값으로 넘어가보자

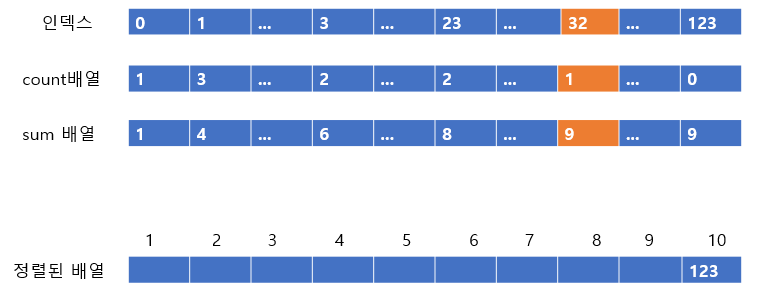
다음 값은 32이다. 32의 count 배열은 1이고, sum은 9이다. 따라서 9번째 인덱스에 32를 넣어주고 count 배열과 sum 배열의 값을 줄여주도록 하자

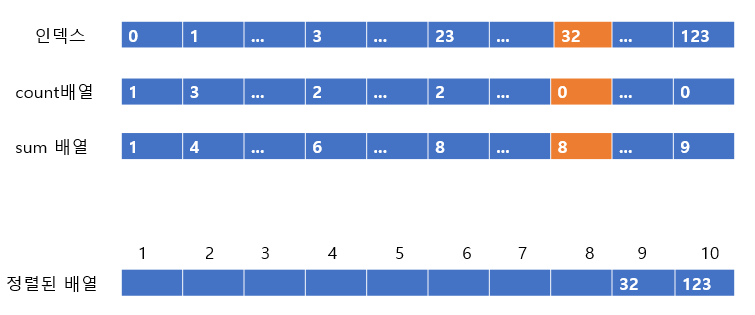
count가 0이 되었으니 다음 칸으로 넘어가도록 하자

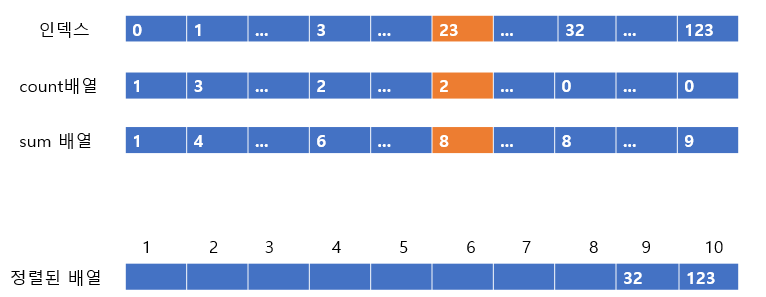
23은 count배열 값이 2이므로, 2번 넣어주어야 한다. 일단 sum배열의 값이 8이므로 8번째 인덱스에 23을 넣어주도록 하자

그리고 count배열과 sum배열의 값을 하나씩 빼준다.

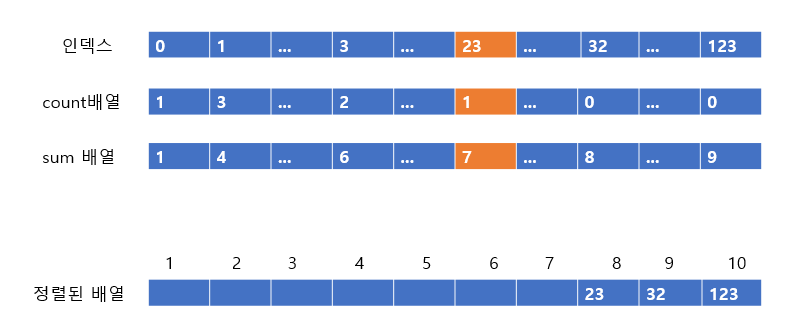
아직 23의 count배열 값이 남아있으므로 sum배열의 값인 7을 보고 정렬된 배열 7번째 인덱스에 23을 넣고 count배열과 sum 배열을 하나씩 줄여준다.

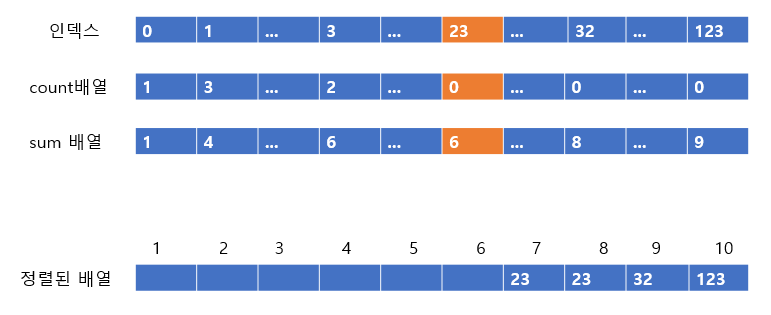
count배열이 0이 되었으므로 다음 칸으로 간다.

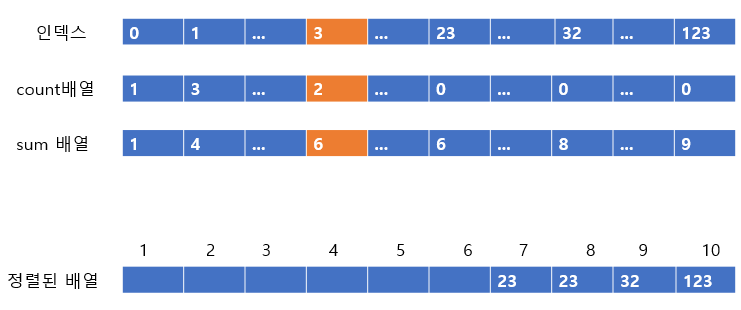
다음 3은 count 배열이 2이고 sum 배열이 6이다. 따라서 6번째 인덱스에 3을 넣어주고 count배열 값과 sum 배열 값을 줄여주도록 한다.

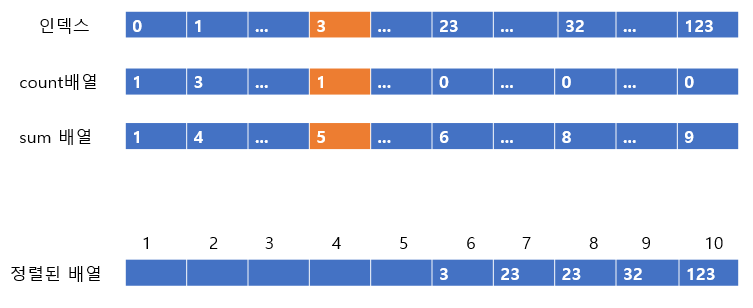
아직 count배열의 값이 남아있으므로 계속 진행한다. sum 배열의 값이 5이므로 3을 5번째 인덱스에 넣어주고 count 배열과 sum 배열 값을 줄여준다.

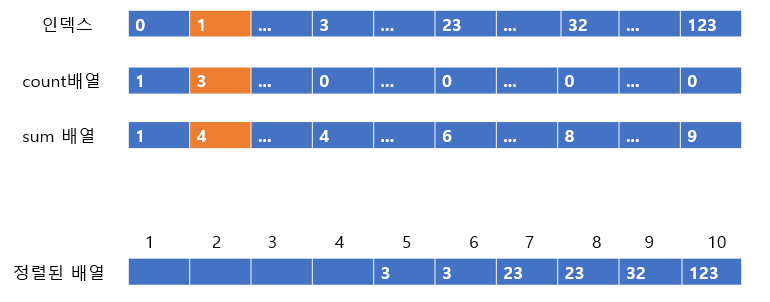
3은 count배열이 0이 되므로 다음 칸으로 간다. 1은 3개가 있다. 이제 필자는 힘들어지고 독자도 지루어질 타이밍이 왔다. 직접 넣으면 어떻게 되는가?

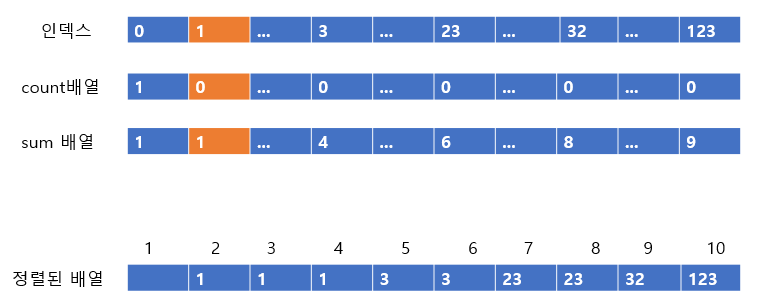
요코롬롬 된다. 마지막 0까지 넣어주면

끝이 된다.

정렬된 배열 [0,1,1,1,3,3,23,23,32,123] 이 된다.

굉장히 쉽고 단순하다.
그런데, 한계는 위의 그림을 보듯이 정렬되지 않은 값의 수들을 인덱스로 지정하여 저장한다는 것이다. 즉, 위의 예에서는 최대 숫자가 123이었으므로, count배열은 최소 124사이즈를 갖어야한다는 것이다.

int count[124];

이렇게 말이다. 잘 생각해보면 엄청난 메모리 낭비라는 것을 알 수 있다. 123사이즈의 메모리에서 사용한 메모리는 결국 0 , 1 , 3, 23, 32, 123 총 6개만 사용했다는 것을 알 수 있다. 이는 엄청난 메모리 낭비이다.

또한, 최대 단점으로는 숫자가 커지면 메모리가 너무 커져 사용할 수 없다는 단점과 음수가 있을 경우 사용하지 못한다는 단점이 있다.

그렇다면 언제 쓰면 되는가?? 사실 문제 풀 때 말고는 구현해 본 적이 없기도 하고 면접 때 설명하는 일 말고는 딱히 없다. 그러나, 쓰이는 곳이 분명하게 존재한다는 것은 안다. 바로 수능 시험 점수를 점수 별로 나열할 때이다.

만약 수능 시험을 보는 인원이 50만 명이라고 하자, 50만명의 국어점수를 정렬하여 백분위를 구해야할 텐데, 50만명의 데이터를 정렬한다면 O(n^2)은 터무니 없고, O(nlogn)이나 O(n)안에 해결해야한다.

그런데, 잘 보면 수능 시험 점수라는 것은 음수도 없고 0~100까지의 점수만을 요구한다. 따라서 이를 계수 정렬로 정렬하는 것이 어렵지 않고 시간 복잡도 이득도 많이 볼 수 있어 사용하면 좋다.

이렇게 명확한 데이터의 제한이 있다면 계수 정렬은 O(nlogn)정렬보다 더 큰 이득을 볼 수 있다.

3. 시간복잡도 분석

O(n) 시간이 어떻게 나오는 걸까??

우리가 만들어야 하는 배열은 단 두 가지이다.

1. count 배열을 만드는 데 필요한 시간은 O(n)이다. 왜냐하면 정렬되지 않은 배열을 쭉 돌아서 해당 값이 몇 개 있는 지 count만 하면 되기 때문이다.

2. sum 배열을 만드는 데 필요한 시간 역시 O(n)이다. 왜냐하면 count 배열을 앞에서부터 순회하여 앞에서 더한 값을 현재 값과 더해주기만 하면되기 때문이다. 여기서는 sum배열을 따로 두었지만, 그냥 count배열과 sum배열을 하나로 합칠 수도 있다. 이는 구현에서 보여드리겠다.

그럼, sum배열과 count배열을 뒤부터 순회하여 값을 채우는 것은 얼마나 시간이 들까?? 이것도 O(n)이다. 결국 sum배열의 0이 나올 때까지 반복하게 되는데, sum배열의 count배열의 합이고, 이는 결국 n과 똑같다. 따라서 O(n)이다.

위와 같은 이유로 계수 정렬은 O(n) 시간 복잡도를 갖게 되는 것이다.

4. 코드

#include <iostream>
#define MAX_DATA_VALUE 200
//계쑤정렬
using namespace std;

int n = 10;
int data[] = {1,23,0,3,32,1,1,23,123,3};
int cnt[MAX_DATA_VALUE];
int ans[MAX_DATA_VALUE];
int main(){
    for(int i = 0; i < n; i++) cnt[data[i]]++;
    for(int i = 1; i <= MAX_DATA_VALUE; i++){
        cnt[i] += cnt[i-1];
    }
    for(int i = n-1; i >= 0; i--){
        int target = data[i];
        ans[cnt[target]-1] = target;
        cnt[target]--;
    }
    for(int i = 0; i < n; i++){
        cout << ans[i] << ' '; 
    }
}

코드만 봐도 굉장히 단순하다.
먼저 , 이 계수 정렬의 최대값은 MAX_DATA_VALUE로 200으로 선정하였다. 즉 0~200까지의 숫자만 나올 뿐 다른 값은 나오지 않는다고 가정하였다.

for문이 총 4개 등장하는데, 마지막꺼는 출력이므로 제외하면 총 3개이다.

첫번째 for문을 보면

for(int i = 0; i < n; i++) cnt[data[i]]++;

각 데이터에 해당하는 수가 몇 번 등장했는 지 세어주도록 한다.

두번째 for문을 보면

for(int i = 1; i <= MAX_DATA_VALUE; i++){
        cnt[i] += cnt[i-1];
    }

cnt를 앞에서부터 순회하여 이전 값을 더해준다. 이는 위에서 sum 배열을 만들 때와 같은데, 이런 식으로도 만들 수 있고, 너무 찜찜하거나 명확하지않다면 sum배열을 만드는 것을 추천한다.

세번째 for문을 보면

for(int i = n-1; i >= 0; i--){
        int target = data[i];
        ans[cnt[target]-1] = target;
        cnt[target]--;
    }

데이터의 맨 뒤부터 순회하기 위해 n-1로 시작하였다. 그리고 data[i]을 통해 target데이터를 가져왔고, target 데이터 몇 번째 인덱스에 저장되어야하는 지 알기위해 cnt[target]을 사용하였다. 여기서 -1을 해주었는데, 이는 기존 계수 정렬은 ans배열을 1부터 채우기 때문에 -1을 하면 0부터 채우는 효과가 있어서 해주었다.

가 다음 cnt을 하나씩 줄이면 된다.
이전 두 번째 for문에서 data에 없는 값도 count해주는 모습을 보았는데, 어차피 data에 해당하는 값만 순회하므로 data에 없는 값도 count해주어도 문제는 없다.

다음은 기수 정렬을 맛보고 정렬 알고리즘을 종료하겠다.