🧭 주제
행렬 기초 완전 통합 정리 — 사칙연산, 항등/역/전치/직교 행렬, 그리고 벡터와의 곱 연산까지
📚 개념
행렬(Matrix)은 2차원 숫자 데이터의 집합으로, 행(row)과 열(column)로 구성된 표 형태를 가진 수학적 개념이다.
하지만 단순한 숫자 배열 그 이상으로, 게임 개발, 그래픽스, 3D 공간 처리에서 매우 중요한 역할을 한다.
특히 3D 그래픽스에서는 객체의 위치(Position), 방향(Rotation), 크기(Scale)을 다루는 데 있어 필수 도구로, 이동(Translation), 회전(Rotation), 크기 변경(Scale) 같은 변화를 수학적으로 표현할 수 있다.
이러한 변화들은 각각 별개의 행렬로 구성할 수 있지만, 실무에서는 이들을 하나의 4x4 행렬로 통합(SRT 변환 통합)하여 효율적으로 처리한다.
즉, 이 행렬은 일종의 '변화의 포탈' 역할을 하며, 벡터가 이 포탈을 통과하면서 위치, 방향, 크기 등이 한 번에 바뀐다.
이처럼 행렬은 단순히 숫자를 담는 구조물이 아닌, 변화 그 자체를 담는 도구이다.
🧾 용어 정리
✅ 행렬과 상수 곱셈
- 행렬의 각 원소에 동일한 스칼라 값을 곱하는 연산
- 예:
k × [a b; c d] = [ka kb; kc kd]

✅ 행렬의 덧셈/뺄셈
- 동일한 크기(같은 행 수와 열 수)의 행렬끼리만 가능
- 같은 위치의 값끼리 더하거나 뺀다
- 예:
[1 2] + [3 4] = [4 6]

✅ 행렬 곱 (행렬 × 행렬)
- 조건: 앞 행렬의 열 수 = 뒤 행렬의 행 수
- 결과: (앞 행렬의 행 수 × 뒤 행렬의 열 수) 크기
- 예:
A (3×2) × B (2×4) = C (3×4) - 곱셈은 내적(dot product)으로 구성된다

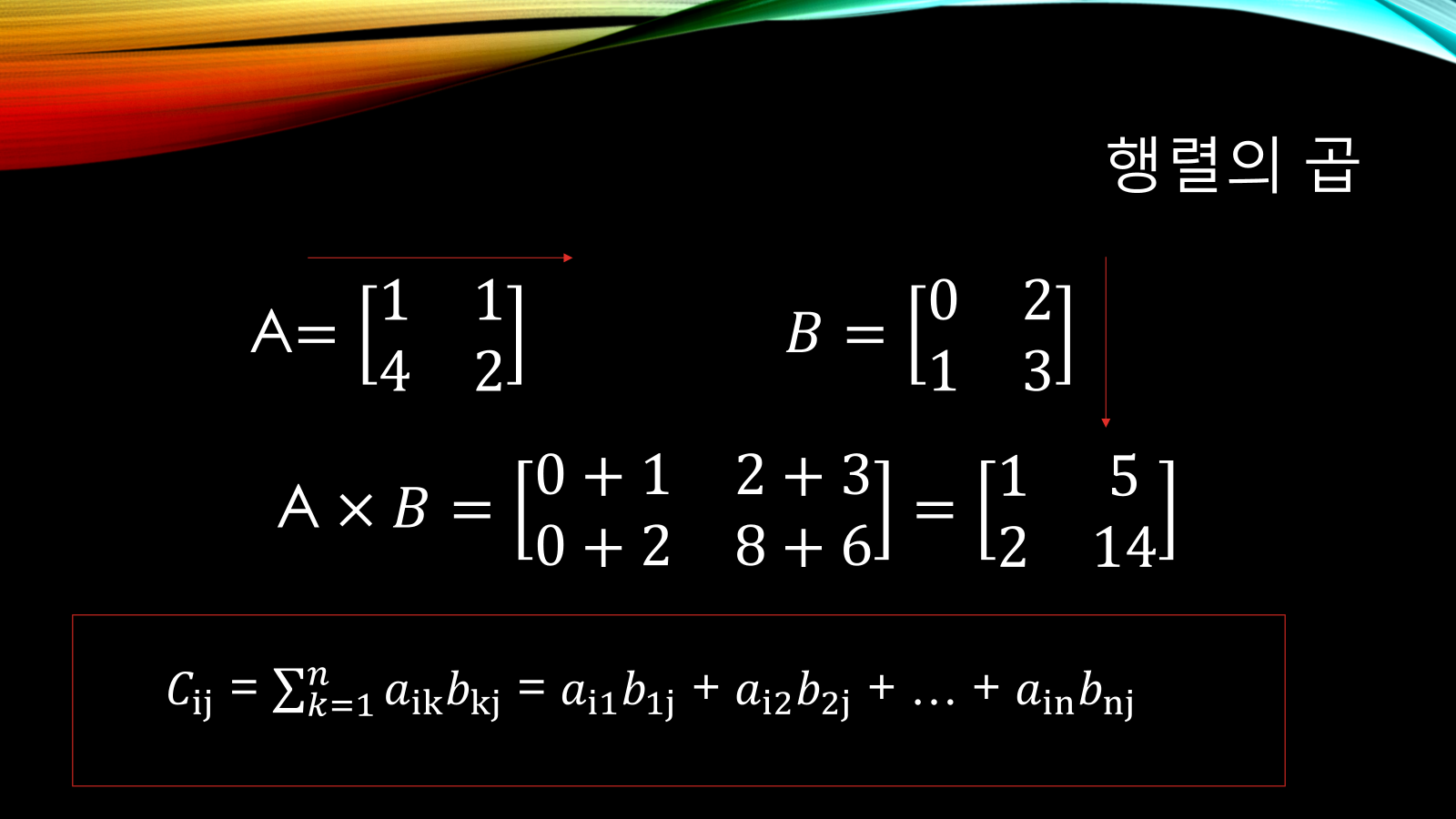
✅ 교환법칙
- 정의: 연산의 순서를 바꿔도 결과가 같아야 성립
- 행렬에서는 성립하지 않음
- 즉,
A × B ≠ B × A
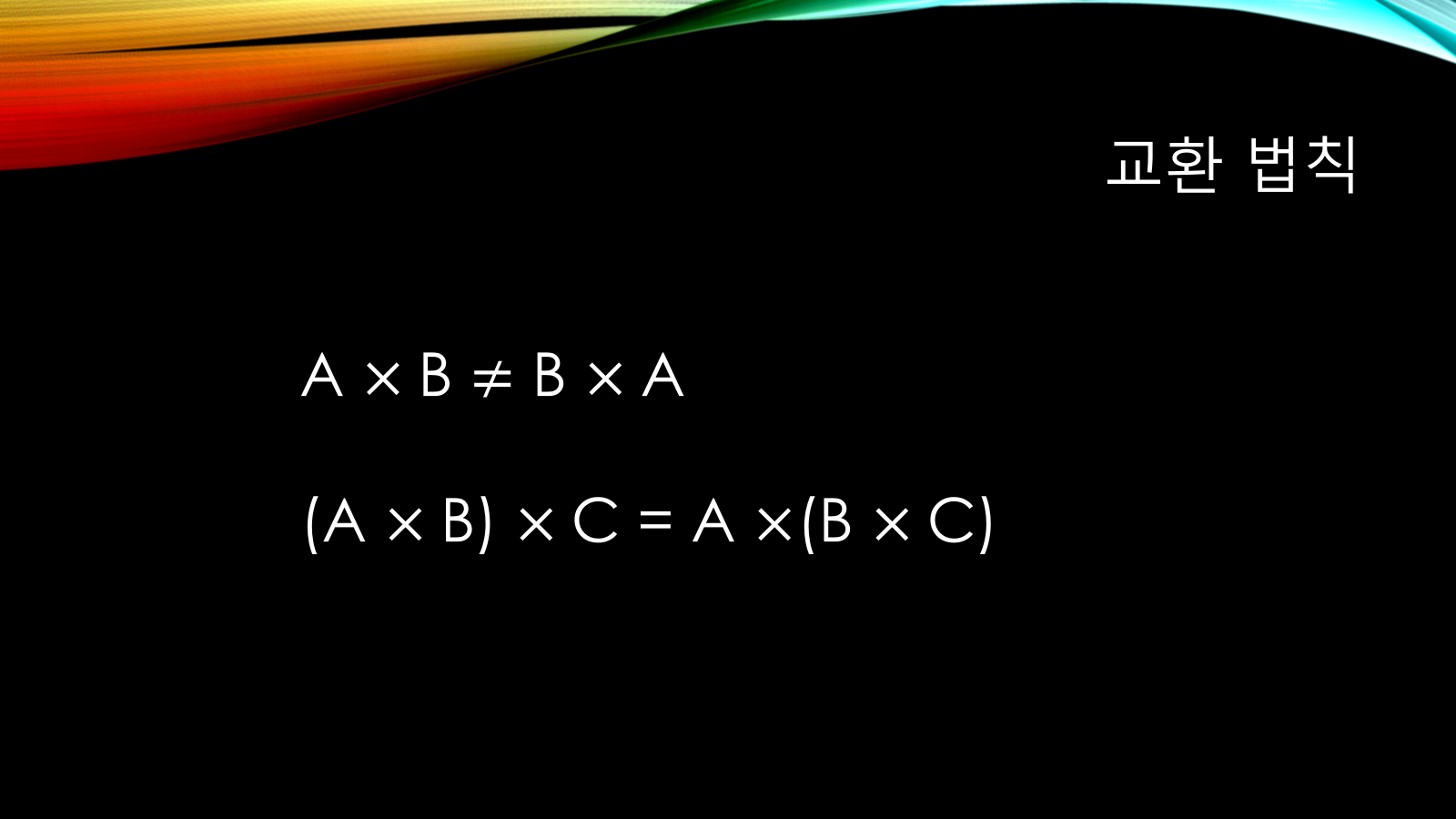
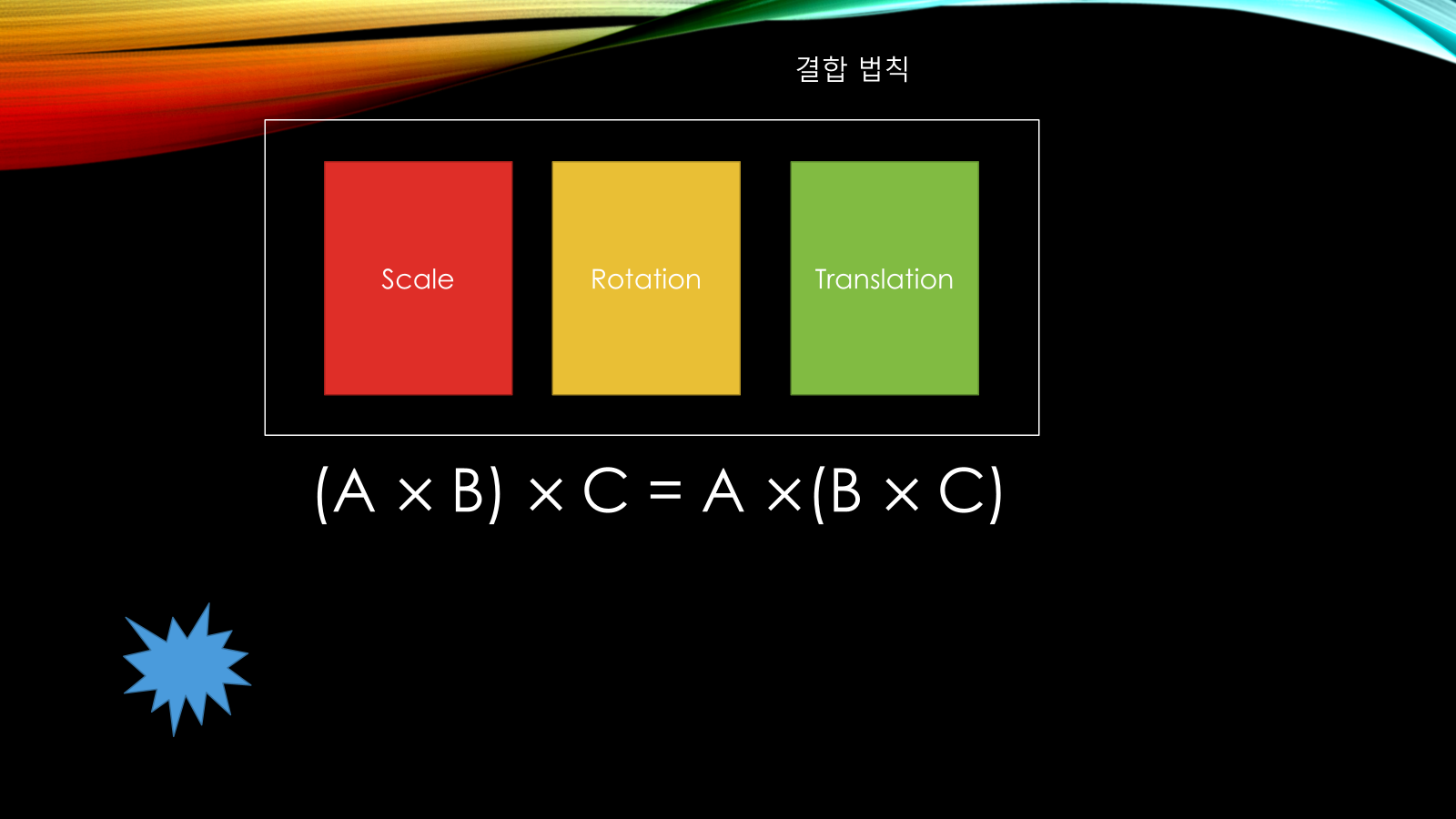
✅ 결합법칙
- 정의: 연산의 그룹을 바꿔도 결과는 같음
- 행렬에서는 성립함
- 즉,
(A × B) × C = A × (B × C)
✅ 항등행렬 (Identity Matrix)
- 모든 성분이 0이고, 대각선만 1인 정사각형 행렬
- 2×2 예시:
I = [1 0; 0 1] - 어떤 행렬 A에 곱해도 A 그대로 나온다
A × I = A I × A = A

✅ 역행렬 (Inverse Matrix)
- 어떤 행렬 A에 대해, A × A⁻¹ = I가 되는 행렬
- A의 효과를 완전히 상쇄시키는 행렬
- 예:
A = [a b; c d], A⁻¹ = 1/(ad - bc) × [d -b; -c a] (단, ad - bc ≠ 0) - 조건: 행렬식(det) ≠ 0 → 그래야 역행렬이 존재함
- 증명식도 가능:
A × A⁻¹ = I A × (A⁻¹ × A) = (A × A⁻¹) × A = I × A = A
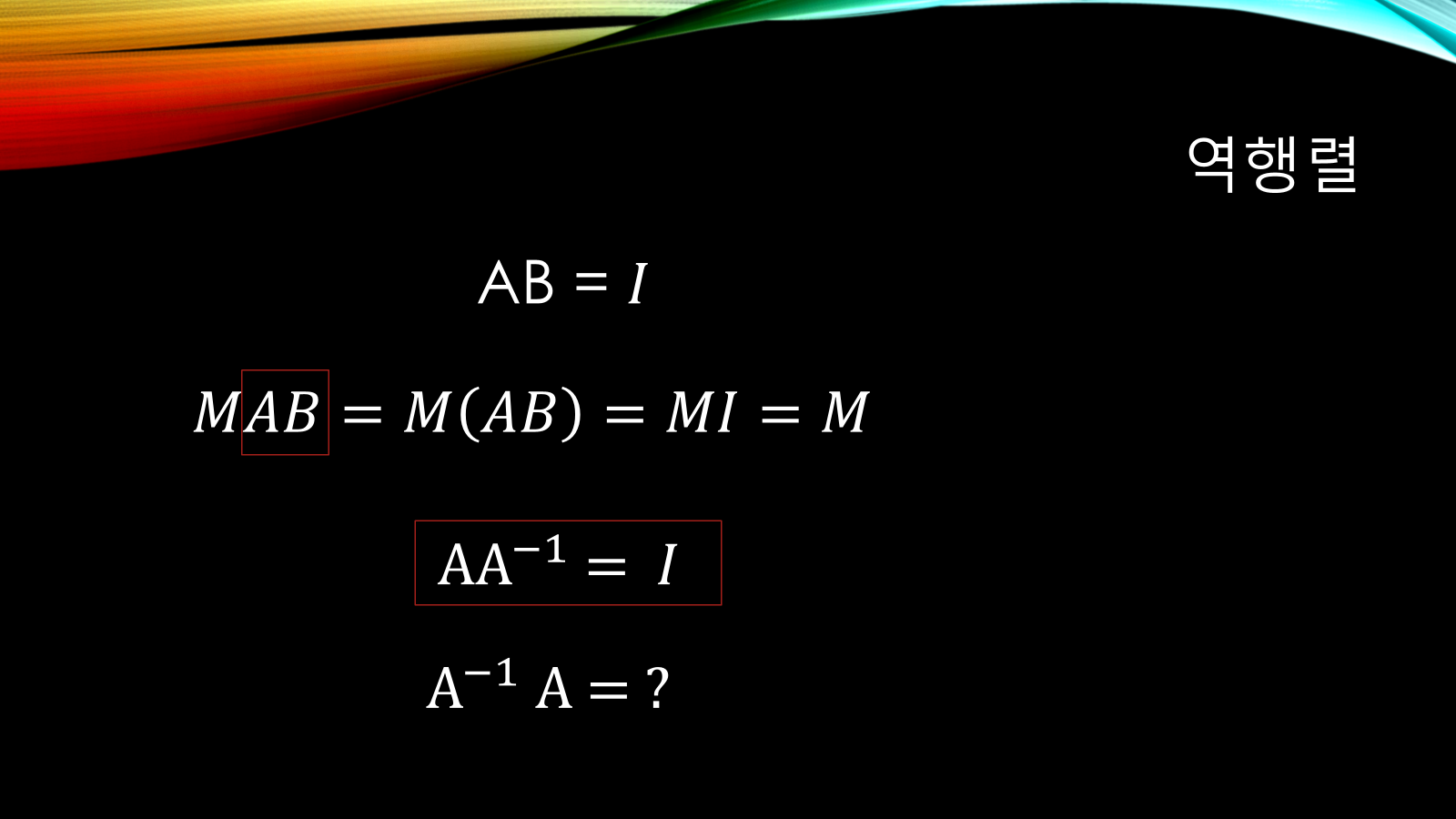
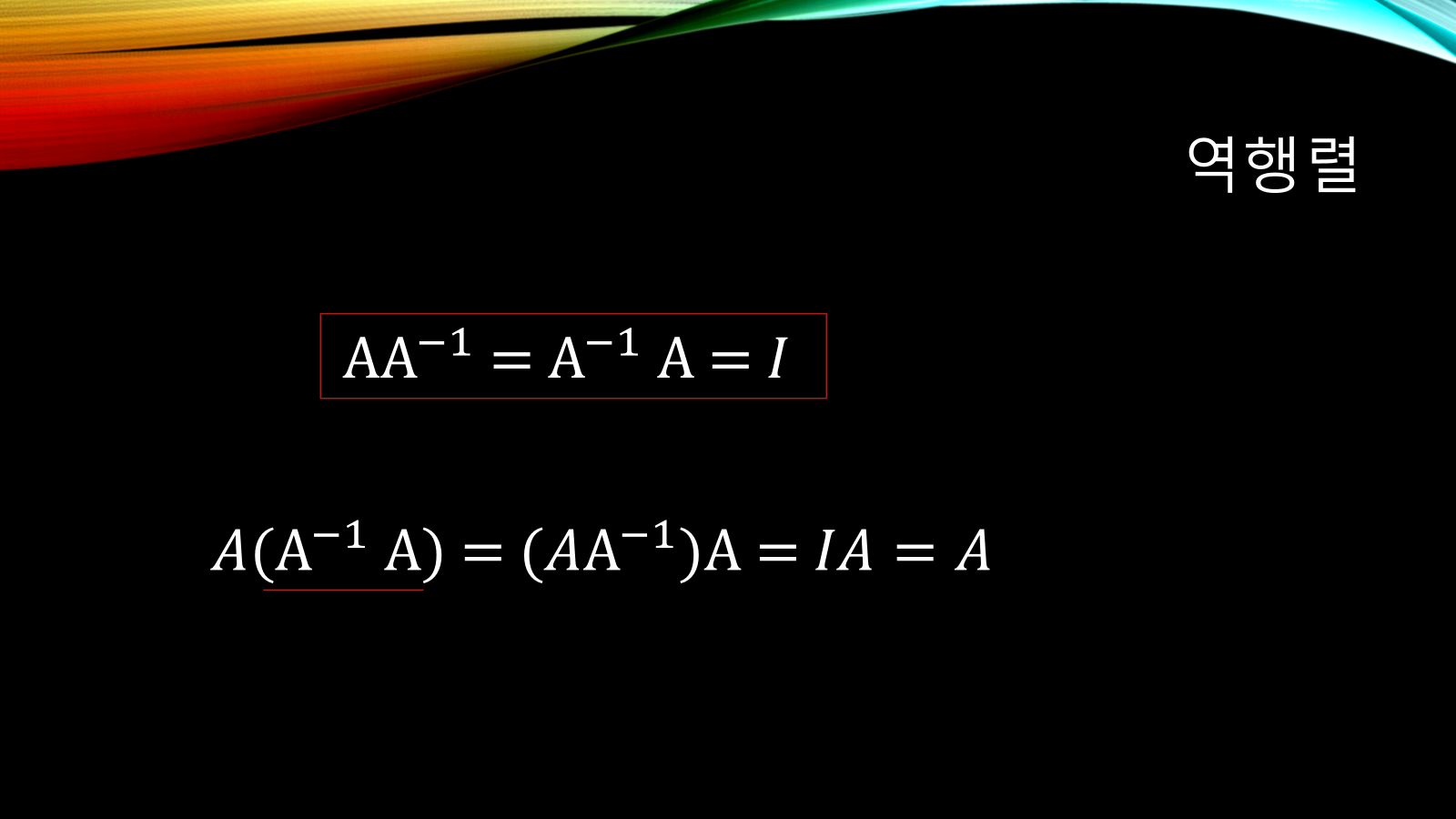
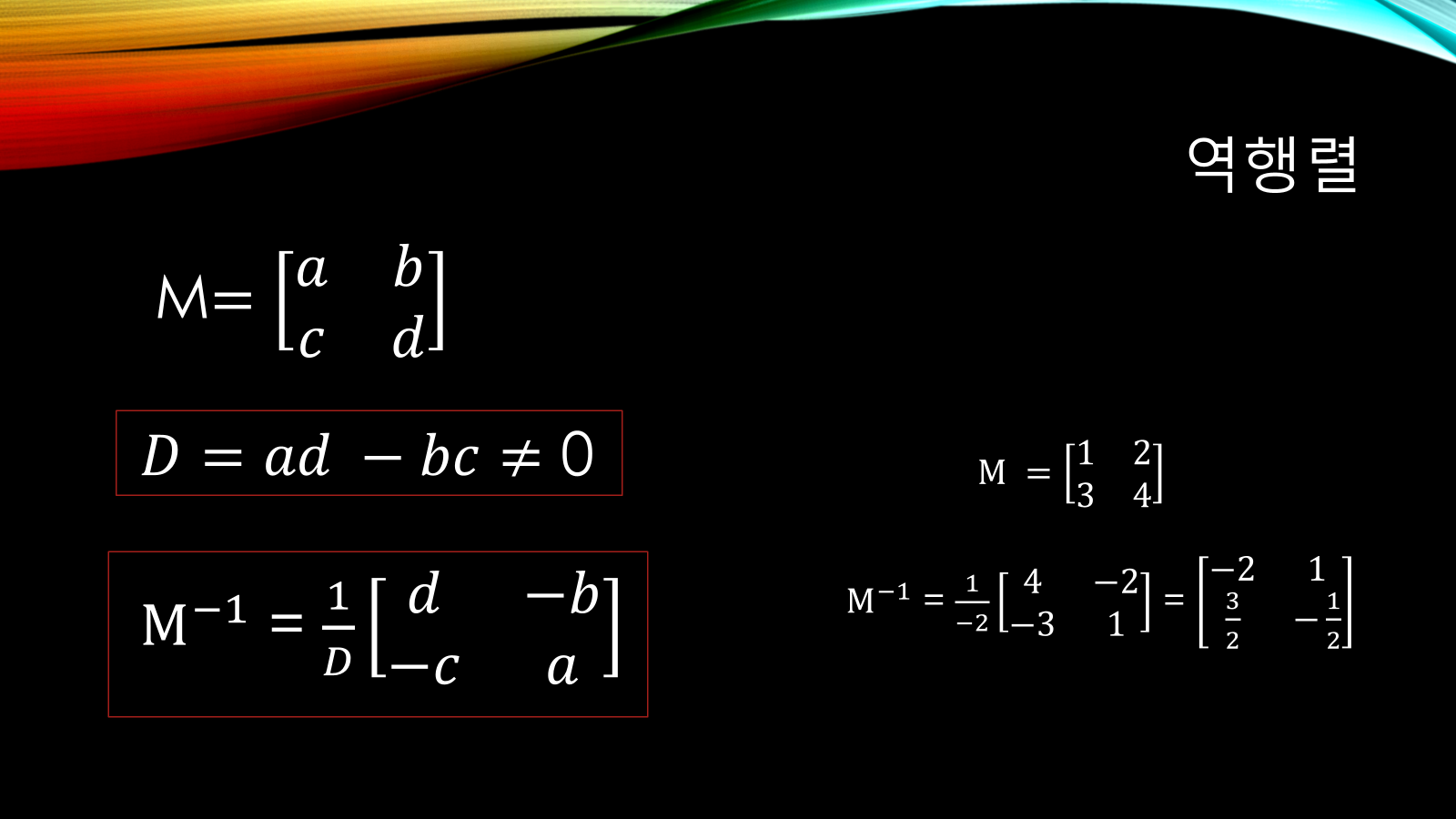
✅ 전치행렬 (Transpose Matrix)
- 행과 열을 뒤바꾼 행렬
- 원소 mᵢⱼ → mⱼᵢ로 바꿈
- 예:
M = [1 2 3; 4 5 6; 7 8 9] Mᵗ = [1 4 7; 2 5 8; 3 6 9] - 성질:
- (Mᵗ)ᵗ = M
- (AB)ᵗ = Bᵗ × Aᵗ
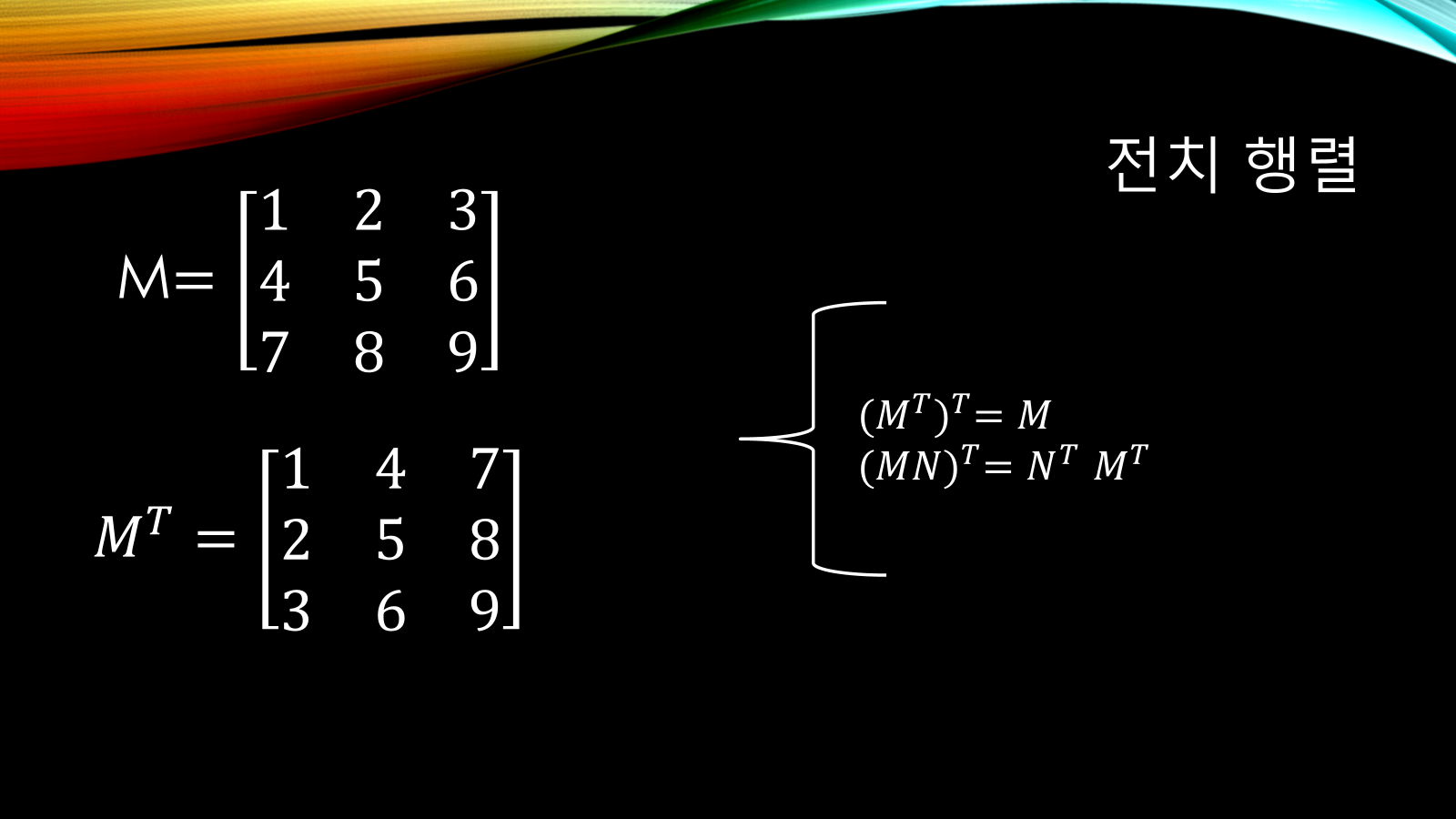
✅ 직교행렬 (Orthogonal Matrix)
- 각 행 또는 열 벡터가 서로 직각(수직) 관계
- 즉, 벡터 간 내적 = 0
- 예시:
M = [0 0 1; 1 0 0; 0 1 0] v₁·v₂ = 0, v₂·v₃ = 0, v₃·v₁ = 0 - 성질:
Mᵗ × M = I M × Mᵗ = I → 전치행렬 = 역행렬
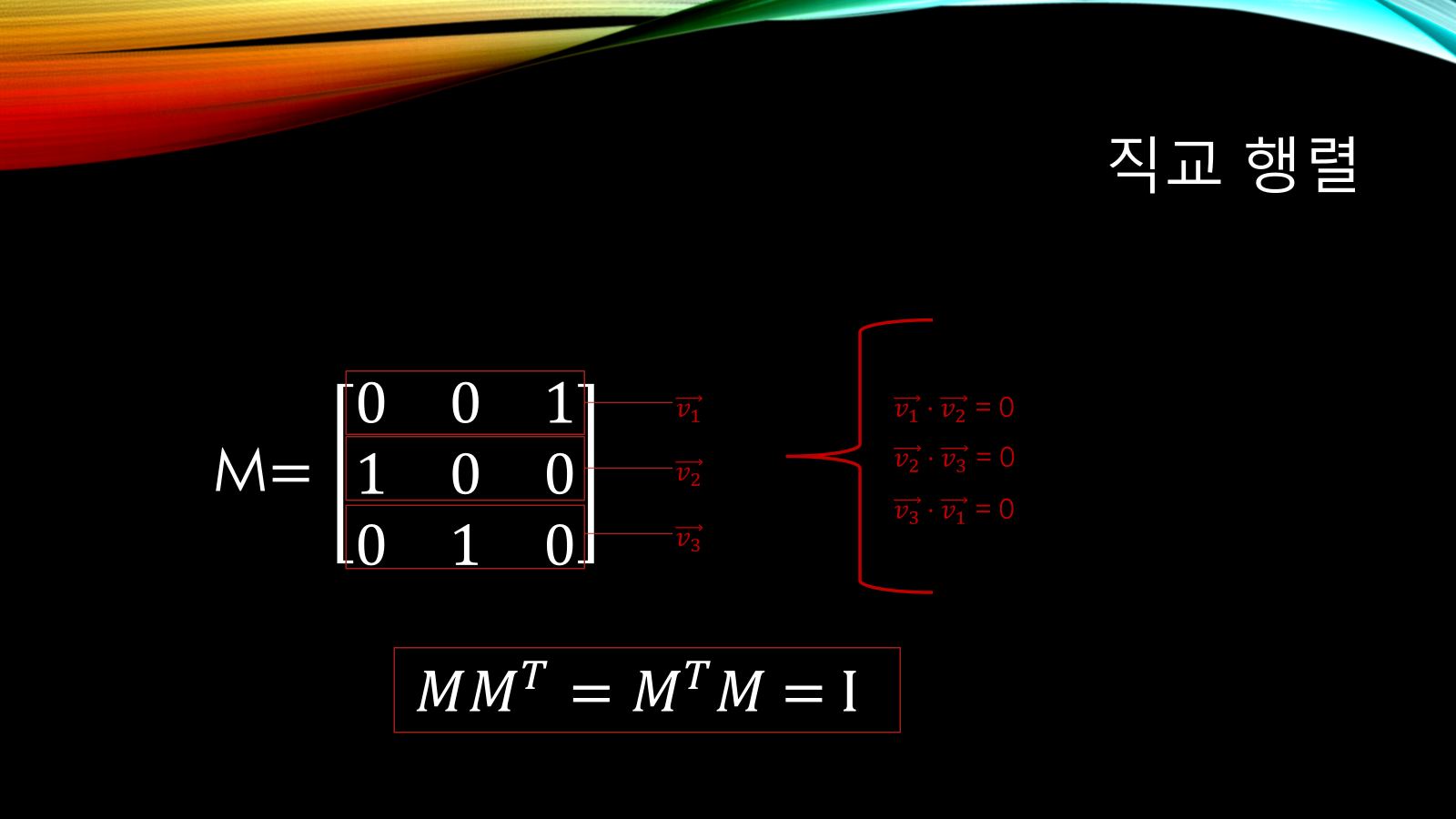
- 직교행렬의 역행렬

✅ 내적 (Dot Product)
- 두 벡터 간의 방향 유사도
- 결과는 스칼라
- 공식:
A · B = |A||B|cosθ - θ가 0일수록 값 ↑, 90°면 0, 180°면 음수
- 용도: 광원 계산, 벡터 간 유사도, 정면 여부 판별
✅ 외적 (Cross Product)
- 두 벡터로부터 수직인 벡터 생성
- 결과는 벡터
- 공식:
A × B = (AyBz − AzBy, AzBx − AxBz, AxBy − AyBx) - 용도: 법선 벡터 계산, 물리 시뮬레이션의 토크 등
🧪 코드 분석 (수식 포함)
✅ 전치행렬
입력
M = [1 2 3; 4 5 6; 7 8 9]출력
Mᵗ = [1 4 7; 2 5 8; 3 6 9]- 대각선을 기준으로 행과 열을 교환한 것
- (i, j) 성분 → (j, i) 성분
✅ 직교행렬 확인
M = [0 0 1; 1 0 0; 0 1 0]- 각 행을 벡터로 보면 서로 수직이다
- v₁·v₂ = 0, v₂·v₃ = 0, v₃·v₁ = 0
- M × Mᵗ = I, Mᵗ × M = I → 전치가 곧 역행렬
✅ 벡터와 4×4 행렬 곱
벡터
v = [x y z 1]행렬
M = [m₁₁ m₁₂ m₁₃ m₁₄
m₂₁ m₂₂ m₂₃ m₂₄
m₃₁ m₃₂ m₃₃ m₃₄
m₄₁ m₄₂ m₄₃ m₄₄]결과
X = x·m₁₁ + y·m₂₁ + z·m₃₁ + m₄₁
Y = x·m₁₂ + y·m₂₂ + z·m₃₂ + m₄₂
Z = x·m₁₃ + y·m₂₃ + z·m₃₃ + m₄₃- 이 연산을 통해 3D 벡터가 스케일, 회전, 이동 변환을 한 번에 적용받음
- 1은 동차좌표계에서 평행 이동 처리에 필요
🎯 핵심
- 행렬은 변화 자체를 담는 구조이며, SRT 변환을 하나의 4x4 행렬로 통합 가능하다.
- 행렬 곱은 여러 변환을 순서대로 적용할 수 있으며, 순서 중요 (교환법칙 불성립, 결합법칙 성립)
- 항등행렬은 연산에 영향을 주지 않고, 변화를 무효화하는 데 사용된다.
- 역행렬은 변화를 되돌리는 도구이며, 존재 여부는 행렬식으로 판단한다.
- 전치행렬은 계산을 단순화하거나 역행렬로 바로 활용될 수 있는 경우(직교행렬) 매우 유용하다.
- 직교행렬은 전치 = 역행렬, 수직성 기반으로 정규화된 변환 행렬이다.
- 벡터 × 행렬 연산은 게임 개발의 본질이다. 위치, 회전, 스케일을 하나의 연산으로 적용 가능하다.
- 동차 좌표계와 4x4 행렬은 3D 연산의 핵심 구조이며, 이 기반 위에서 모든 그래픽 연산이 수행된다.
