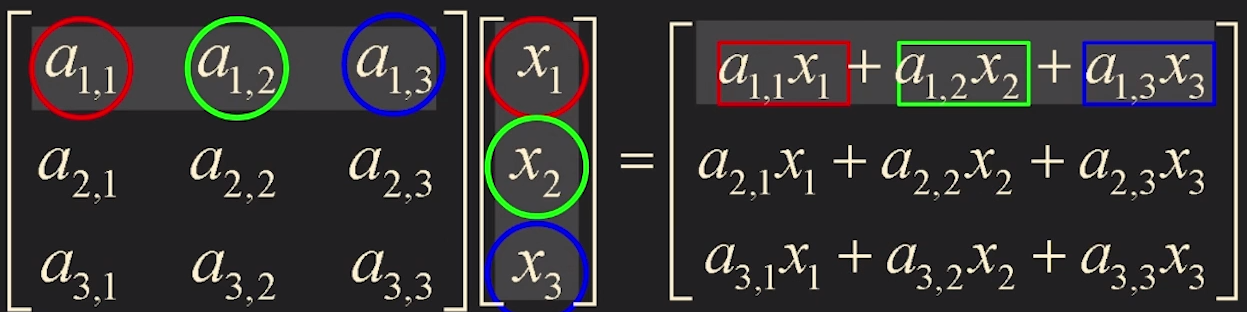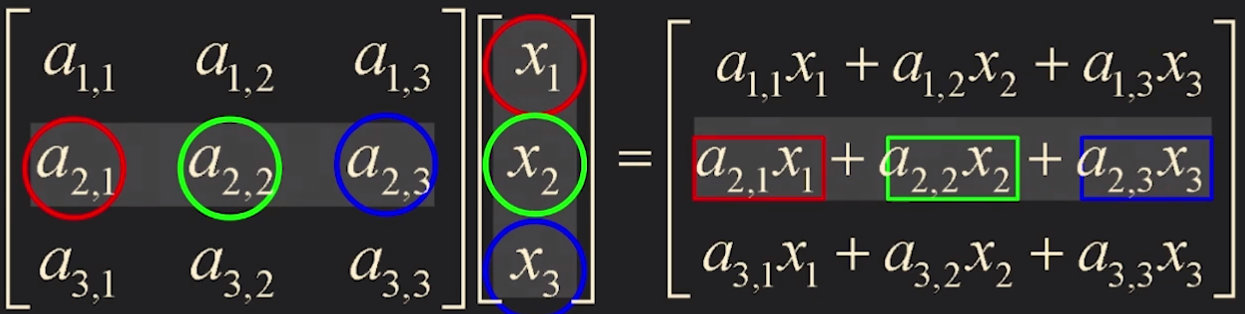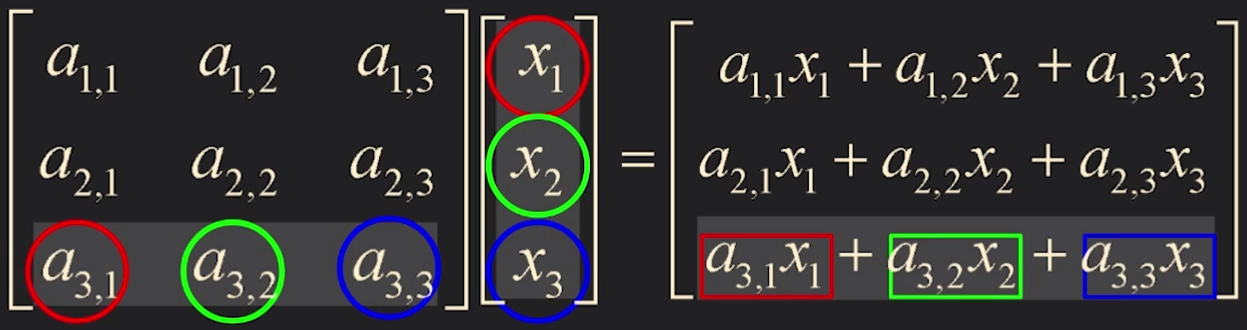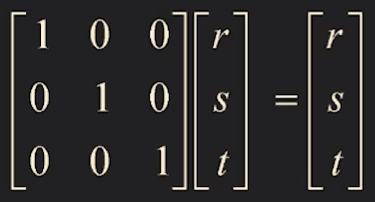1.4 The Matrix Equation Ax=b

조범희 선생님의 선형대수학개론 강의를 듣고 공부하며 정리한 내용입니다.
정말 좋은 강의힙니다. 강추합니다. 링크

Ax: product of A and x

A is m x n matrix, with columns $a_1, \cdots, a_n$

x is in $\mathbb{R}^n$

$A\bold{x} = \begin{bmatrix}a_1\ a_2\ \cdots\ a_n\end{bmatrix} \begin{bmatrix} x_1\\ \vdots\\ x_n\end{bmatrix} = x_1\bold{a_1} + x_2\bold{a_2} + \cdots + x_n\bold{a_n}$

A x is the linear combination of the columns of A using the corresponding entries in x as weights

 

Example 1. Matrix Equation

$\begin{bmatrix} 1 & 2 & -1\\ 0 & -5 & 3 \end{bmatrix} \begin{bmatrix} 4\\ 3\\ 7 \end{bmatrix} =4\begin{bmatrix} 1\\ 0 \end{bmatrix} +3\begin{bmatrix} 2\\ -5 \end{bmatrix} +7\begin{bmatrix} -1\\ 3 \end{bmatrix} =\begin{bmatrix} 3\\ 6 \end{bmatrix}$

$\begin{bmatrix} 2 & -3\\ 8 & 0\\ -5 & 2 \end{bmatrix} \begin{bmatrix} 4\\ 7 \end{bmatrix} =4\begin{bmatrix} 2 \\ 8 \\ -5 \end{bmatrix} +7\begin{bmatrix} -3\\ 0\\ 2 \end{bmatrix} =\begin{bmatrix} -13\\ 32\\ -6 \end{bmatrix}$

 

Example 2. Vector equation to matrix equation

$x_1\bold{v_1} + x_2\bold{v_2} + x_3\bold{v_3} = \begin{bmatrix} \bold{v_1} & \bold{v_2} & \bold{v_3} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}$

순서가 중요하다. x가 앞에 있으면 안된다. 절대로!

 

Example 3. System of linear equations to matrix equation

$\begin{aligned} x_1 + 2x_2 - x_3 = 4\\ -5x_2 + 3x_3 = 1 \end{aligned}$

$x_1\begin{bmatrix} 1\\ 0 \end{bmatrix} +x_2\begin{bmatrix} 2\\ -5 \end{bmatrix} x_3\begin{bmatrix} -1\\ 3 \end{bmatrix} = \begin{bmatrix} 4\\ 1 \end{bmatrix}$

$= \begin{bmatrix} 1 & 2 & -1\\ 0 & -5 & 3 \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} =\begin{bmatrix} 4\\ 1 \end{bmatrix}$

 

Example 4. More efficient way to compute matrix equation

$\begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3}\\ a_{2,1} & a_{2,2} & a_{2,3}\\ a_{3,1} & a_{3,2} & a_{3,3} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} =\begin{bmatrix} a_{1,1}x_1 + a_{1,2}x_2 + a_{1,3}x_3\\ a_{2,1}x_1 + a_{2,2}x_2 + a_{2,3}x_3\\ a_{3,1}x_1 + a_{3,2}x_2 + a_{3,3}x_3 \end{bmatrix}$

더 쉽게는 빨간 + 초록 + 파랑 을 자리에 맞게 넣어주면 된다

 

 

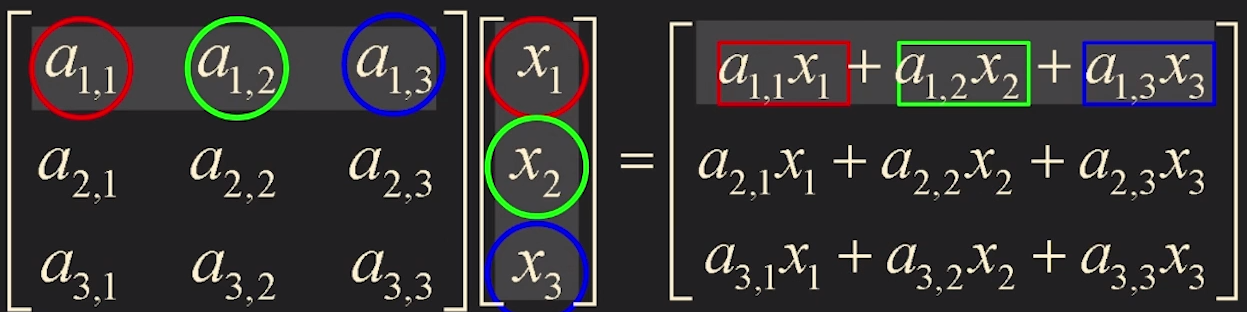
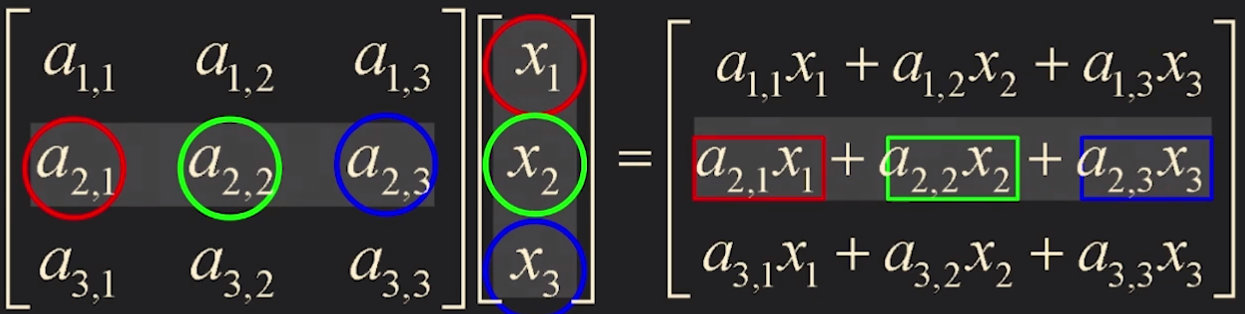
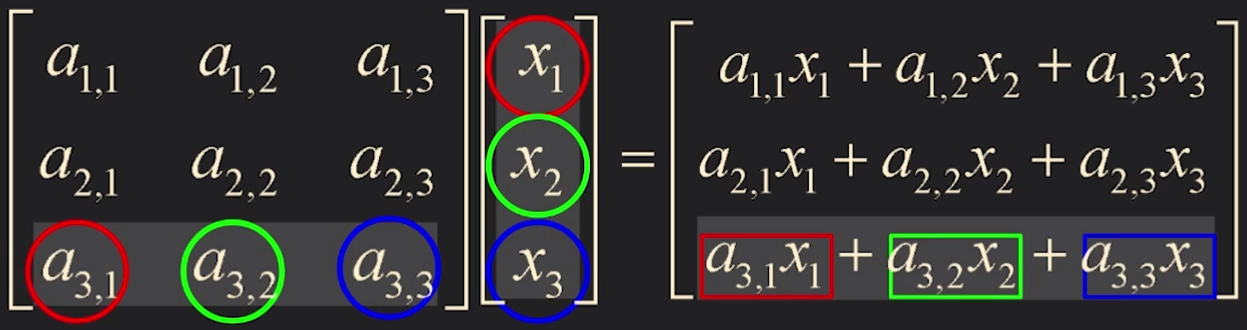
Identity Matrix I

$*\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}$*

A x = b 꼴에서 matrix A가 Identity Matrix 이면 A x = x가 된다.

 

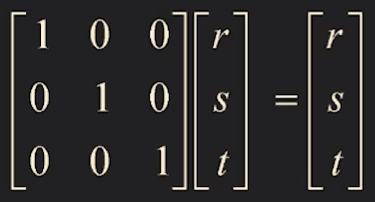
Theorem 3.

A is m x n matrix, with columns $a_1, \cdots, a_n$

x is in $\mathbb{R}^n$

matrix equation : $A\bold{x} = \bold{b}$

vector equation : $x_1\bold{a_1} + x_2\bold{a_2} + \cdots + x_n\bold{a_n} = \bold{b}$

augmented matrix : $\begin{bmatrix} \bold{a_1}\ \bold{a_2}\ \cdots\ \bold{a_n}\ \bold{b} \end{bmatrix}$

have the same solution set!

여기까지는 무리없이 이해가 가능하다.

 

Theorem 4.

A is m x n matrix, with columns $a_1, \cdots, a_n$

The followings are all true or all false;

a. For each b in $\mathbb{R}^n$, A x = b has a solution

b. Each b in $\mathbb{R}^n$ is a linear combination of the columns of A

c. The columns of A span $\mathbb{R}^n$

d. (Not augmented matrix) A has a pivot position in every row.

 
여기서는 c에 유의해서 이해해야 한다.

A가 $\mathbb{R}^n$ 을 span 한다는 것은, A의 column vector들을 a1, a2, ..., an이라 했을때,

$\mathbb{R}^n$ 내의 $c_1, c_2, \cdots, c_n$ 에 의해 생긴 ($c_1, c_2, \cdots, c_n$ 등은 실수라는 뜻)

$c_1a_1 + c_2a_2 + ... + c_na_n$이 $a_1$부터 $a_n$에 의해 span된 space라는 뜻이다.

즉 이는 a, b, d와 동치가 된다 (조범희 선생님 답변을 참고하여 이해하였다)

 

Theorem 5.

If A is an m x n matrix, u and v are vectors in $\mathbb{R}^n$, and c is a scalar, then;

$A(\bold{u}+\bold{v}) =A\bold{u}+A\bold{v};\\ A(c\bold{u})=c(A\bold{u})$

너무나 당연한 것처럼 보이지만, c가 scalar일 때만 가능하다는 것을 명심하자. c가 vector라면 성립할 수도 있고 성립하지 않을 수도 있다