목차

• 이진탐색트리
• 이진탐색트리 연산

---

이진탐색트리

이진탐색트리(Binary Search Tree) 정의

• 이진탐색(binary search)의 개념을 트리 형태의 구조에 접목한 자료구조
  

필요성

• 단순한 구조
• 노드의 키들의 정렬된 결과를 쉽게 얻을 수 있음
• 이진 검색과 비슷하게 아주 빠른 탐색

이진탐색트리 조건

• 각 노드 키가 왼쪽 서브트리에 있는 키들보다 크고, 오른쪽 서브트리에 있는 키들보다 작다.
• 일반적으로 키 값이 같은 노드는 복수로 존재x (딕셔너리와 유사)
  ![]

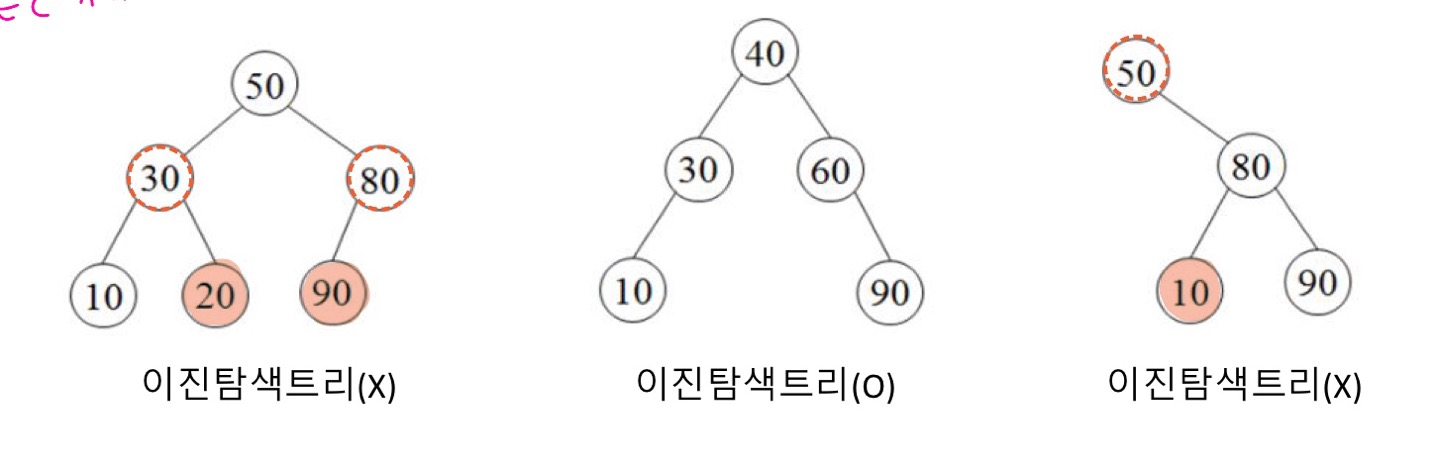
첫 번째 그림은 이진탐색트리가 아니다.
1) 30의 오른쪽 노드인 20은 30보다 커야 함
2) 80의 왼쪽 노드인 90은 80보다 작아야 함

두 번째 그림은 이진탐색트리이다.
1) 모든 왼쪽 노드는 점점 작아지고
2) 모든 오른쪽 노드는 점점 커지기 때문

세 번째 그림은 이진탐색트리가 아니다.
1) 50의 오른쪽 노드는 모두 50보다 커야 한다.
2) 10은 50보다 작다.

이진탐색트리 구조

• 노드a의 왼쪽 서브트리는 a보다 작은 값들을 지닌 노드들로 이루어짐
• 노드a의 오른쪽 서브트리는 a보다 큰 값들을 지닌 노드들로 이루어짐
• 루트의 왼쪽 서브트리와 오른쪽 서브트리는 이진탐색트리(재귀적 정의)

이진탐색트리 클래스

이진탐색트리에 사용되는 노드

• key: 키 값을 저장
• value: 값
• left: 왼쪽 자식 참조
• right: 오른쪽 자식 참조

class Node:
	def __init__(self, key: int, value: Any):
      self.key = key # 키
      self.value = value # 값
      self.left = None # 왼쪽 자식
      self.right = None # 오른쪽 자식

이진탐색트리 클래스

• BinarySearchTree: 클래스 명
• 생성자는 멤버변수 root 생성

class BinarySearchTree:
	def __init__(self):
    	self.root = None # 멤버변수가 root뿐 # 빈 탐색트리

노드 삽입

삽입 연산

• 이진탐색트리의 조건을 유지한 채 새로운 노드 삽입하기
• 왼쪽 자식노드 작게, 오른쪽 자식노드 크게
• 이진탐색트리는 노드로 구현함

노드 삽입 과정

1) 삽입 위치 찾기(=k의 부모 찾기)

• k: 삽입할 노드의 키🗝️
• k가 루트 키🗝️보다 작으면 왼쪽 서브트리 삽입
• k가 루트 키🗝️보다 크면 오른쪽 서브트리 삽입
• 위 과정 반복하며 최종 삽입 위치 선정

2) 새로운 노드 삽입위치에 추가

재귀적으로 노드 삽입하는 방법

이진탐색트리의 구조🏗️

• 노드a의 왼쪽 서브트리는 a보다 작은 값들을 지닌 노드들로 이루어짐
• 노드a의 오른쪽 서브트리는 a보다 큰 값들을 지닌 노드들로 이루어짐
• 루트의 왼쪽 서브트리와 오른쪽 서브트리는 이진탐색트리(재귀적 정의)

• sroot: (전체)서브트리의 루트노드
• k: 삽입할 노드의 키🗝️
• sroot<k: 오른쪽 서브트리에 전체 트리에서 노드 삽입하는 함수 호출(재귀)
• sroot>k: 왼쪽 서브트리에 전체 트리에서 노드 삽입하는 함수 호출(재귀)

노드 삽입 구현

• insert(): 전체 트리에 노드 삽입하는 함수
  - key: 삽입할 노드 키🗝️
  -value: 삽입할 노드 값🔢
  -return: 없음(동작만 수행)
• insert_to_subtree(): (오/왼) 서브트리에 노드 삽입하는 함수
  - key: 삽입할 노드 키🗝️
  -value: 삽입할 노드 값🔢
  -sroot: 서브트리의 루트 노드🪢
  -return: 없음

class BinarySearchTree:
    def __init__(self):
        self.root = None
    
    def insert(self, key: int, value: Any):
        """전체 트리에 노드 삽입"""
        if self.root: # 루트 노드가 있다면
            self.insert_to_subtree(key, value, self.root) #서브트리에 새 노드 삽입
        else: # 루드 노드가 없다면
            self.root = Node(key, value) # 새 노드 루트노드로 지정
        
    def insert_to_subtree(self, key: int, value: Any, sroot: Node): # sroot의 자식으로 새로운 노드 삽입(오/왼은 후에 정함)
        """서브트리에 노드 삽입"""
        if key < sroot.key: # 새 노드의 키가 서브트리의 루트(sroot) 노드의 키보다 작다면 왼쪽 서브트리에 넣는다.
            if sroot.left:
                # sroot의 왼쪽자식이 이미 있으면,  자식의 자식으로 새 노드 삽입(왼쪽자식의 서브트리에 새 노드 삽입)
            else:
                # sroot의 왼쪽자식이 없으면, sroot의 왼쪽자식으로 노드 삽입
                sroot.left = Node(key, value)
        elif key > sroot.key: # key가 서브트리의 루트의 키보다 크면 오른쪽 서브트리에 새 노드를 넣는다.
            if sroot.right:
                # sroot의 오른쪽자식이 이미 있으면, 자식의 자식으로 새 노드 삽입(= 오른쪽자식의 서브트리에 새 노드 삽입)
                self.insert_to_subtree(key, value, sroot.right)
            else:
                # sroot의 오른쪽자식이 없으면, sroot의 오른쪽자식으로 새 노드 삽입
                sroot.right = Node(key, value)

노드 탐색

탐색 연산(≒ 삽입 연산)

• 노드의 키로 노드를 탐색하여 노드의 값🔢을 리턴

탐색 알고리즘

• k: 탐색하는 노드의 키🗝️
• root: 전체 노드 루트의 키🗝️
• k == root: 첫 번째 탐색에서 성공, 루트노드의 값🔢 리턴
• k > root: 오른쪽 서브트리에서 k 탐색
• k < root: 왼쪽 서브트리에서 k 탐색
• 위 과정 반복, 더 이상 서브트리가 없다면 탐색 실패🚫

노드 탐색 구현

• find(): 전체트리에서 노드 탐색
  • 탐색 성공 시 노드의 값 리턴🔢
  • 탐색 실패 시🚫 None 리턴
• find_in_subtree(): 서브트리에서 노드 탐색
  • 탐색 성공 시 노드의 값 리턴🔢
  • 탐색 실패 시🚫 None 리턴

    def find(self, key: int)-> Any:
        """전체트리에서 노드 탐색 후 값 리턴"""
        return self.find_in_subtree(key, self.root)
        """서브트리 노드 탐색에서 sroot를 root로 변경하면 전체 탐색
    def find_int_subtree(self, key: int, sroot: Node) -> Any:
        """서브트리에서 노드 탐색 후 값 리턴"""
        if not sroot: # 노드가 존재하지 않으면(None) => 빈 트리
            return None # 탐색 실패 🚫
        elif key == sroot.key: # 찾는 키와 srooot 키 동일
            return sroot.value # 원트 성공
        elif key < sroot.key: # 찾는 키가 sroot 키보다 더 작음
            return self.find_in_subtree(key, sroot.left) # 오른쪽 서브트리에 대해 재귀호출
        else: # 찾는 키가 sroot 키보다 더 큼
            return self.find_in_subtree(key, sroot.right) # 왼쪽 서브트리에 대해 재귀호출

최소키 탐색

• 이진탐색트리에서 키 값이 가장 작은 노드 찾기
  - 왼쪽 서브트리가 더 이상 없을 때까지 왼쪽 서브트리만 살펴보면 됨
  

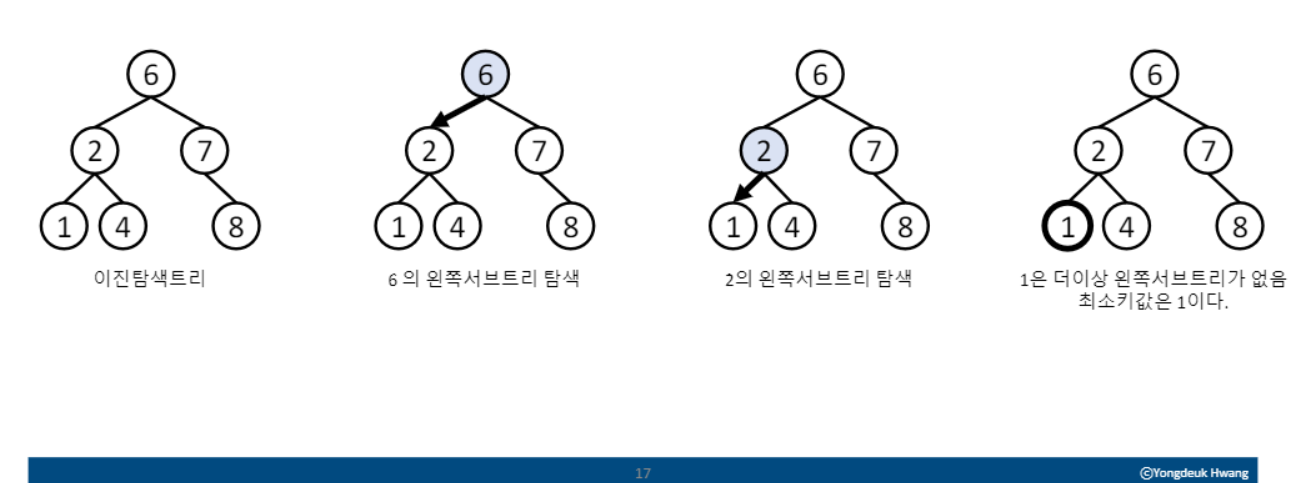
최대키 탐색

• 이진탐색트리에서 키 값이 가장 큰 노드 찾기
  - 오른쪽 서브트리가 더 이상 없을 때까지오른쪽 서브트리만 살펴보면 됨
  

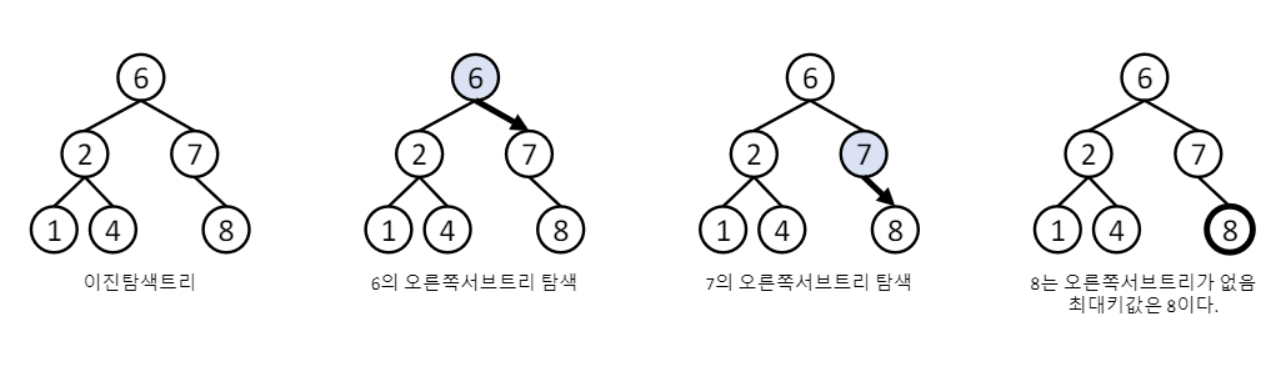
최소키/최대키 탐색 구현

• min_node(): 서브트리에서 최소키를 가지는 노드 리턴🪢
• max_node(): 서브트리에서 최대키를 가지는 노드 리턴🪢

def min_node(self, sroot: Node):
    """서브트리에서 최소키값을 가지는 노드 리턴"""
    if not sroot: # 빈 트리
        return None # 탐색 실패 🚫
    else: # 빈 트리가 아니면
        if sroot.left: # 왼쪽 자식이 존재할 경우
            return self.min_node(sroot.left) # 재귀적으로 탐색
        else: # 왼쪽 자식이 존재하지 않을 경우
            return sroot # 현 서브트리의 루트 노드

def max_node(self, sroot: Node):
    """서브트리에서 최대키값을 가지는 노드 리턴"""
    if not sroot: # 빈 서브트리
        return None # 탐색 실패 🚫
    else:
        if sroot.right: # 오른쪽 서브트리가 존재할 경우
            return self.max_node(sroot.right) # 재귀적으로 서브트리 탐색 
        else: 
            return sroot # 탐색 성공

노드 삭제

• 삽입, 탐색보다 훨씬 복잡함

삭제 경우

1. 자식 노드가 없는 노드를 삭제하는 경우 -> 짱 쉬움
2. 자식이 1개인 부모 노드를 삭제하는 경우 -> 쉬움
3. 자식이 2개인 부모 노드를 삭제하는 경우 -> ⭐복잡

1. 자식 노드가 없는 노드를 삭제하는 경우

1) 삭제할 노드를 탐색한다.
2) 부모노드를 이용하여 삭제할 노드가 있는 위치로 간다.
3) 삭제할 노드를 None으로 대체한다.

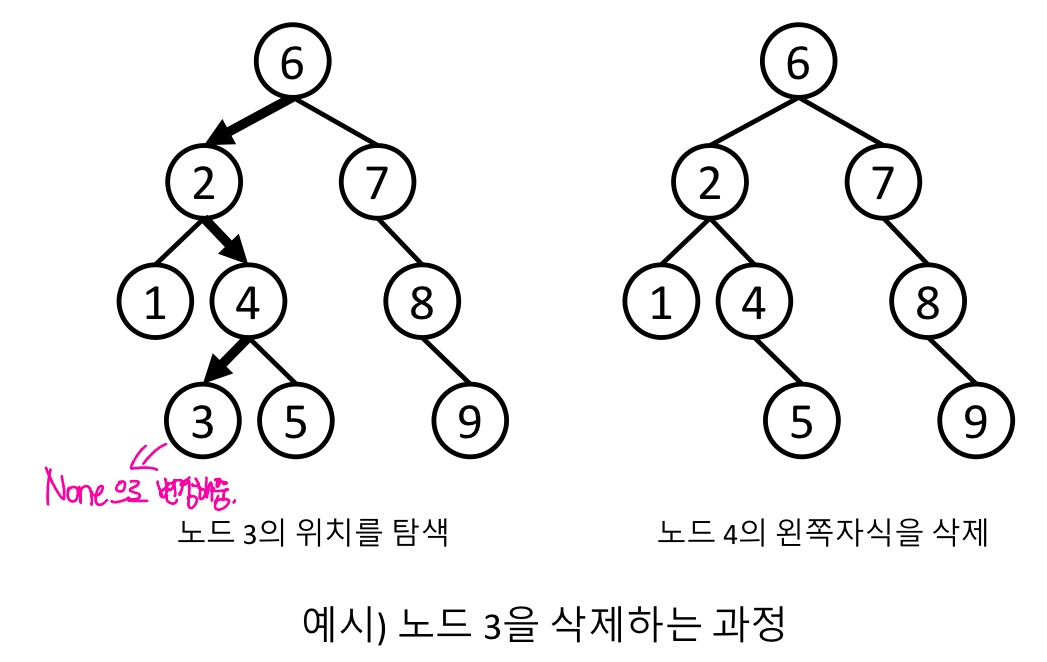
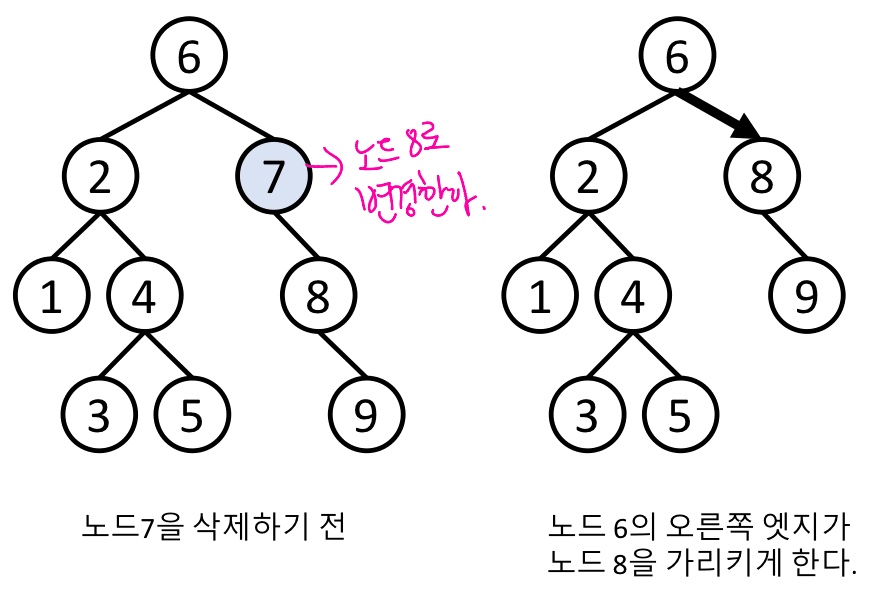
2. 자식 노드가 1개인 노드를 삭제하는 경우

1) 삭제할 노드를 탐색한다.
2) 삭제할 노드의 자식노드를 탐색한다. -> 1개이면 3)으로, 0개이면 1번으로간다.
3) 삭제할 노드의 자식노드를 삭제할 노드의 부모노드와 연결시킨다.

⭐3. 자식노드가 2개인 노드를 삭제하는 경우

• 이진탐색트리에서는 자식노드의 수가 최대 2개이다.
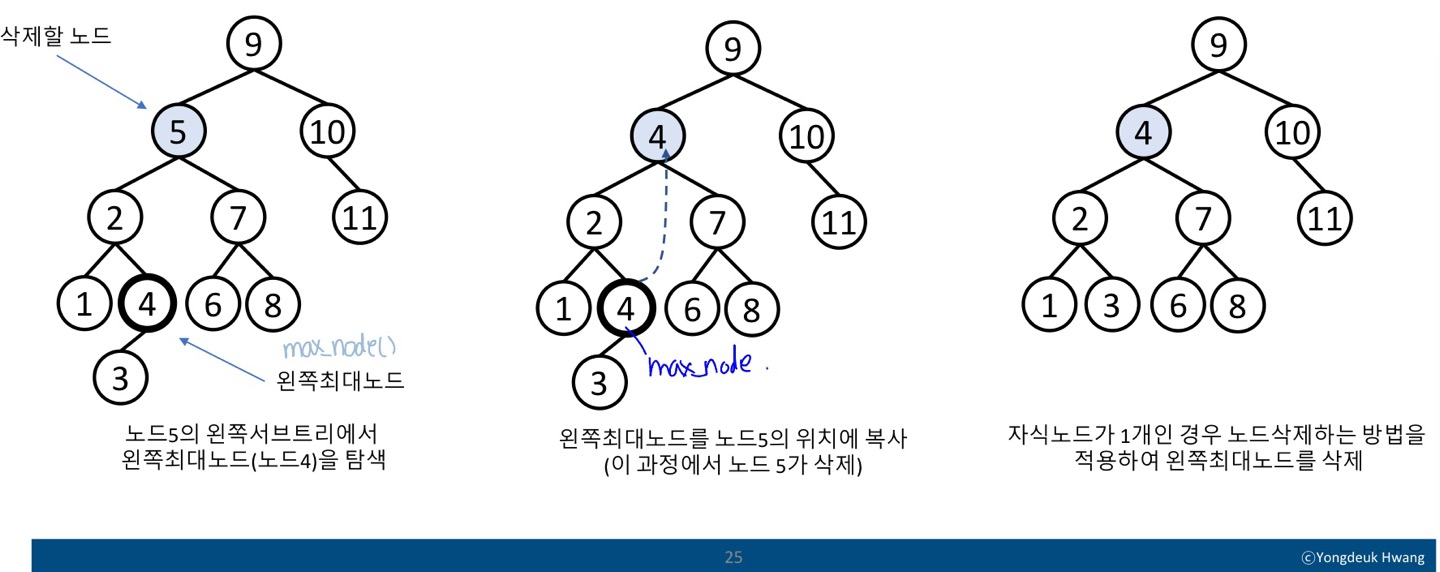
  1) 삭제할 노드의 왼쪽서브트리에서 키값이 가장 큰 노드 탐색
• 이 노드를 왼쪽최대노드라 하자.
  2) 왼쪽최대노드의 키와 값을 삭제할 노드에 복사한다. -> 삭제할 노드 대체
  3) 기존에 있던 왼쪽최대노드를 삭제한다. -> 중복제거

• 예: 노드 5를 삭제하는 과정
  

• 오른쪽이 아닌 왼쪽최대노드를 탐색하는 이유

• 그래야 왼쪽 서브트리의 값은 항상 더 작고 오른쪽 서브트리의 값은 항상 더 크다는 이진탐색트리의 조건을 유지할 수 있다.

노드 삭제 구현

• delete(): 전체트리에서 노드 삭제
• delete_in_subtree()
  • 서브트리에서 특정 key값을 갖는 노드 삭제
  • ⭐⭐⭐삭제 후 서브트리의 루트노드🪢 리턴⭐⭐⭐

def delete(self, key: int)-> Node:
    """전체트리에서 노드 삭제"""
    self.root = self.delete_in_subtree(key, self.root)

def delete_in_subtree(self, key: int, sroot: Node)-> Node:
    """서브트리에서 노드 삭제"""
    if not sroot: # 서브트리가 비어있으면
        return None
    
    if key < sroot.key: # 삭제할 키가 서브루트 키보다 작으면 왼쪽 서브트리 탐색
        sroot.left = self.delete_in_subtree(key, sroot.left) # 재귀
    elif key > sroot.key: # 삭제할 키가 서브루트 키보다 크면 오른쪽 서브트리 탐색
        sroot.right = self.delete_in_subtree(key, sroot.right) # 재귀
    else: # if key == sroot.key:
        if sroot.left and sroot.right: # 자식이 둘인 노드 삭제
            # 서브트리의 루트노드를 왼쪽서브트리의 최대 노드로 교체(key와 value만)
            max_node = self.max_node(sroot.left) # 왼쪽에서 최대키값을 가지는 노드
            sroot.key = max_node.key
            sroot.value = max_node.value

            # 왼쪽서브트리에서 최대 노드를 삭제
            sroot.left = self.delete_in_subtree(max_node.key, sroot.left) # 재귀
        elif sroot.left: # 왼쪽 자식만 있는 노드삭제
            sroot = sroot.left
        elif sroot right: # 오른쪽 자식만 있는 노드 삭제
            sroot = sroot.right
        else: # 자식이 없는 노드 삭제
            sroot = None
            
    return sroot # 서브트리의 루트노드를 리턴

트리순회

• 모든 노드를 한번씩만 방문
• 노드 방문 순서에 따라 종류 구분(깊이우선탐색/너비우선탐색)

깊이우선탐색(Depth-first search, DFS)

• 서브트리를 재귀적으로 순회
• 세로 방향을 우선적으로 순회

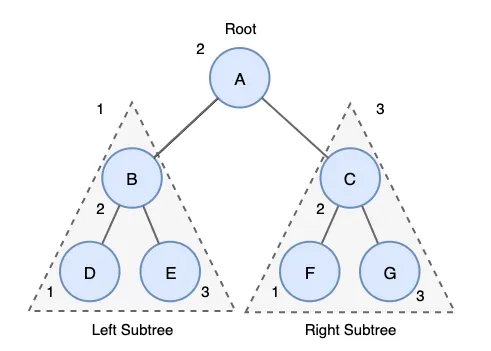
중위순회

• L→N→R 순서로 방문하는 것
• 예) D → B → E → A → F → C → G
  

이미지 출처

중위순회 구현

• inorder(): 중위순회
  • 왼쪽서브트리를 중위순회
  • 루트를 방문
  • 오른쪽서브트리를 중위순회

def inorder(self, sroot: Node)-> None:
    """중위순회"""
    if sroot: # sroot가 존재해야 함
        self.inorder(sroot.left) # 왼쪽서브트리를 중위순회
        print(sroot.key, end = ' ') # sroot 방문 <=> key 출력
        self.inorder(sroot.right)

전위순회

• N→L→R 순서로 방문하는 것
• 예) A → B → D → E → C → F → G
  

이미지 출처

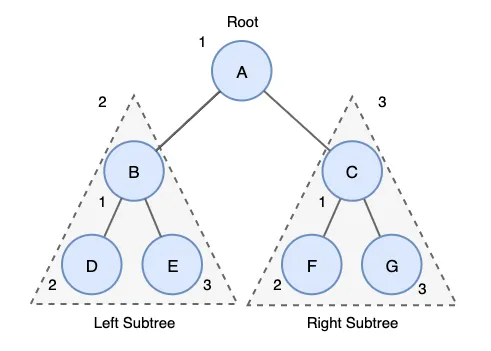
전위순회 구현

• preorder(): 전위순회
  • 루트 방문
  • 왼쪽 서브트리를 전위순회
  • 오른쪽서브트리를 전위순회

def preorder(self, sroot: Node)-> None: 
    """전위순회"""
    if sroot:
        print(sroot.key, end = ' ') # sroot 키 출력
        self.preorder(sroot.left) # 왼쪽서브트리 전위순회
        self.preorder(sroot.right) # 오른쪽서브트리 전위순회

후위순회

• L→R→N 순서로 방문하는 것
• 예) D → E → B → F → G → C → A
  

이미지 출처

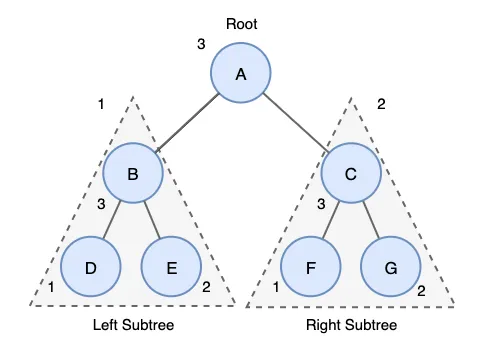
후위순회 구현

• postorder(): 후위순회
  • 왼쪽서브트리를 후위순회
  • 오른쪽서브트리를 후위순회
  • 루트 방문

def postorder(self, sroot: Node)-> None:
    """후위순회"""
    if sroot:
        self.postorder(sroot.left) # 왼쪽서브트리 후위순회
        self.postorder(sroot.right) # 오른쪽서브트리 후위순회
        print(sroot.key, end = ' ') # sroot 키 출력

너비우선탐색(Bread-first search, BFS)

• 큐를 이용하여 레벨순서대로 순회
• 가로 방향을 우선적으로 탐색
• 지그재그
  

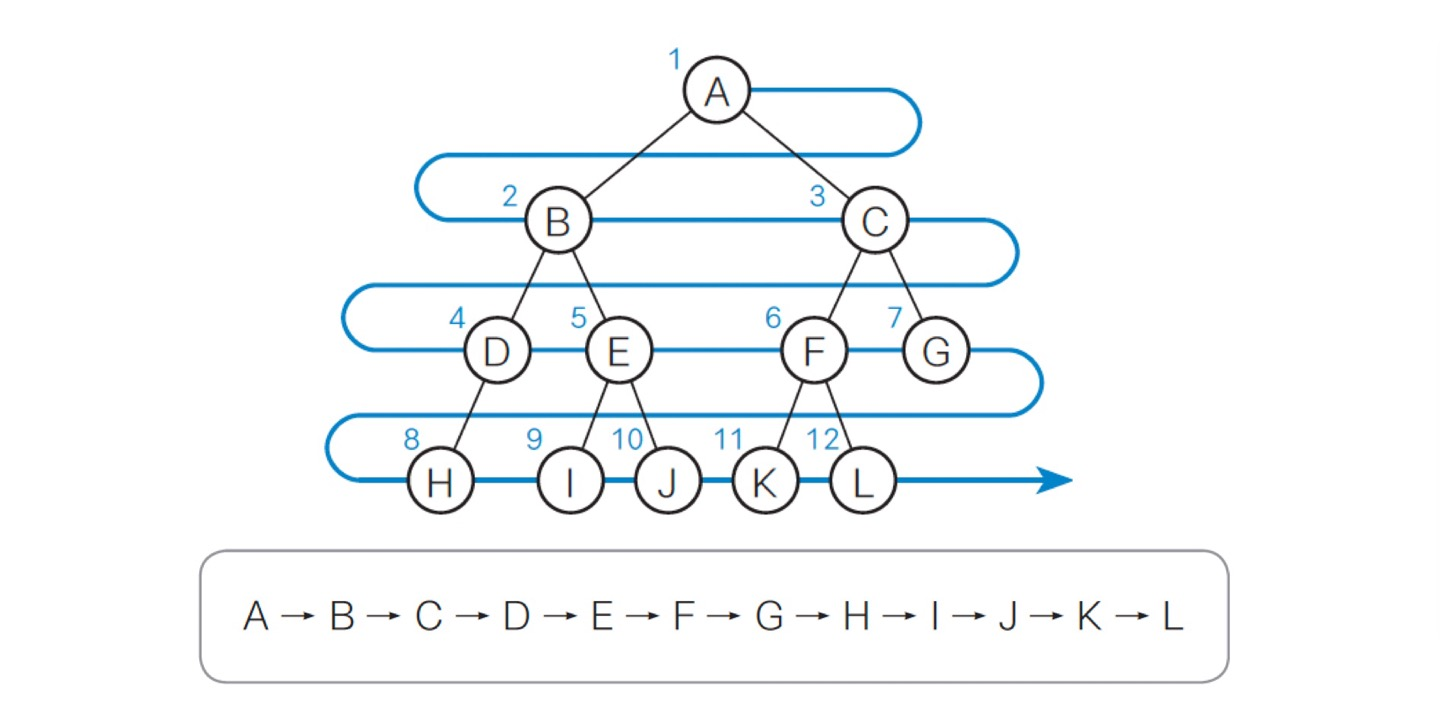
• 레벨순회 알고리즘
  • 큐가 비어있지 않으면
    1) 큐에서 노드를 꺼낸다.
    2) 노드를 방문한다.
    3) 노드의 자식들을 큐에 넣는다.

레벨순회 구현

def levelorder(self, sroot: Node)-> None:
    """레벨순회"""
    queue = deque()
    queue.append(sroot) # 큐에 노드를 넣는다.
    while queue:
        node = queue.popleft()
        if node: # 노드가 비어있지 않는 경우
            print(node.key, end = ' ') # 노드 방문
            queue.append(node.left) # 노드왼쪽자식 큐 추가
            queue.append(node.right) # 노드 오른쪽자식 큐 추가

트리순회 연습하기

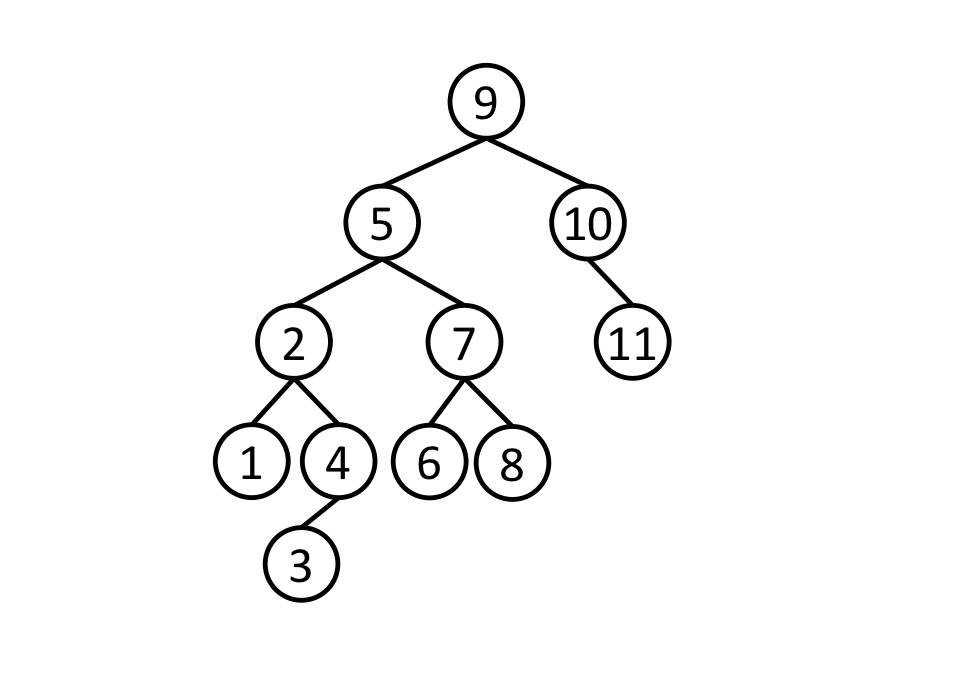
• 중위순회(L→N→R): 1→2→3→4→5→6→7→8→9→10→11
• 전위순회(N→L→R): 9→5→2→1→4→3→7→6→8→10→11
• 후위순회(L→R→N): 1→3→4→2→6→8→7→5→11→10→9
• 레벨순회: 9→5→10→2→7→11→1→4→6→8→3

• 주의: 노드가 아닌 서브트리 관점으로 봐야 한다.
  4보다 3이 후위순회에서 더 우선순위가 높은 것도 같은 맥락이다.
  4는 N(중앙)노드이고 3은 L(왼쪽)노드이기 때문이다.

이진탐색트리 특징

이진탐색트리의 단점

• 트리의 모양이 한쪽으로 치우치면 탐색/삽입/삭제 연산의 시간복잡도가 O(N)에 가까워진다.

이진탐색트리의 단점을 보완한 자료구조

• AVL 트리
  • Adelson-Velsky and Landis가 개발한 트리로 어려워서 수업 시간에 다루지 않았음
• 레드-블랙 트리
  • 각 노드가 레드 or 블랙의 속성을 가진 트리

이진탐색트리 연산 시간복잡도 비교

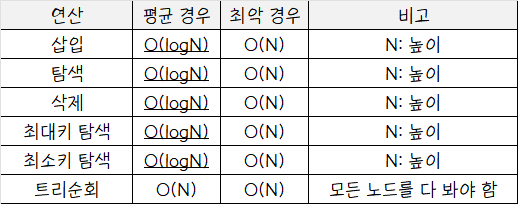
• 삽입, 탐색, 삭제연산 대부분의 경우 O(logN)이지만 트리의 모양이 한쪽으로 치우치는 등 특별한 경우에만 O(N)이다.