Method 중심으로 리뷰 진행했습니다. 먼저 3D Reconstruction의 개념부터 보고 넘어가겠습니당
Preliminary
3D Reconstruction
3D Reconstruction이란 2D 이미지로부터 3D 장면을 생성하고 렌더링하는 컴퓨터 비전 기술이다.
기존 3D Representation 기술
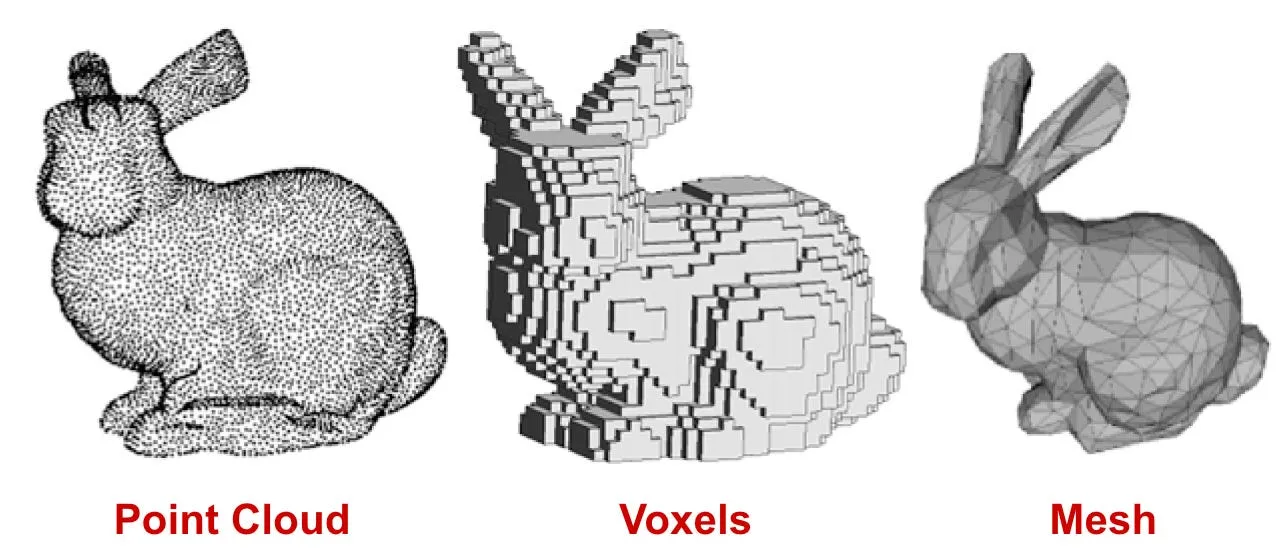
1. Explicit Representation - Point cloud, voxel, mesh
-
point cloud: 3D 공간을 점들의 집합으로 표현하는 방법이다.
-
voxel: 3D 공간을 격자 형태의 부피 픽셀로 나누어 표현하는 방법으로, 부피 픽셀의 크기에 따라 해상도가 결정된다.
쉽게 2D에서는 픽셀 단위로 나누는 것처럼, 3D에서는 voxel단위로 나눈다고 생각하면 된다.
3D 공간을 작은 정육면체로 나누고 물체가 점유하는 공간을 채우면 voxel 형태로 표현할 수 있게 된다.
-
mesh: 3D 공간을 2D 다각형이 서로 연결된 형태로 표현하는 방법이다. 꼭짓점(vertex), 엣지(edge), 면(face)으로 구성돼 있다.
2. Implicit Representation - NeRF

(a)
scene을 통과하는 camera ray를 쏜 다음에 샘플링하여 sampled set of 3D point를 생성한다.
그리고, 위의 point들의 위치 정보(Position)인 (x,y,z)와 카메라의 방향 정보(Direction)인 (θ,ϕ)을 구한다.
(모델의 input: 5D coordinate (x,y,z,θ,ϕ))
(b)
위의 정보를 입력으로 사용하여 신경망(MLP)에 넣고, 출력값으로 RGB 색상 값과 volume density 밀도 값 σ 을 얻는다.
(모델의 output: (RGBσ))
(c)
Volume Rendering 방법을 사용하여 RGB값과 density값을 누적하여 2D image로 만든다.
(d) 다음 과정은 미분 가능하기 때문에 **예측값과 Ground Truth (실제값) 차이의 loss값을 줄이며 모델을 최적화**하는 Gradient Descent를 사용한다.
3DGS란?
3차원 공간에 있는 점들을 Gaussian 분포로 표현하여 3D 데이터의 밀도와 형태를 효과적으로 시각화하는 3D reconstruction 기법이다.
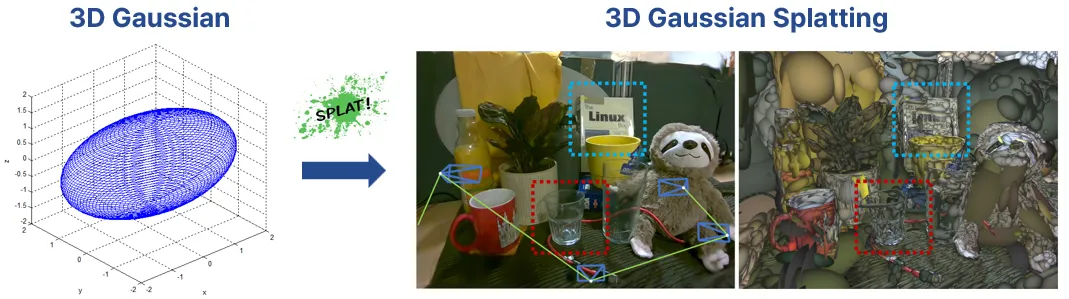
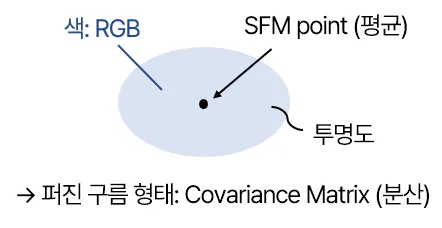
3D Gaussian은 타원체의 형태로, 평균과 공분산(3x3행렬) 값을 갖고 있다. 색상, 투명도 값까지 정의하면 3D Gaussian Splatting이 가능하다. 투명도(opacity)는 해당 가우시안이 scene에 얼마나 기여하는지 나타낸다.
3D Gaussian을 흩뿌린(splatting) 것이 3D Gaussian Splatting이다.
Geometry를 세세하게 묘사할 수 있도록 Gaussian의 수, 위치, 크기, 회전, 색상값, 투명도를 조절하여 정밀한 scene을 묘사한다.
Splatting ??
Splatting은 데이터를 공간적으로 확산시키는 기술이다. 따라서 3D Gaussian Splatting은 어떤 공간 상에서 3D Gaussian들이 분포되어 있는 형식을 뜻한다.
SfM ??
SfM은 하나의 객체를 여러 시점에서 찍은 multi-view 이미지들로부터 3D structure와 camera pose를 복원하는 과정이다.
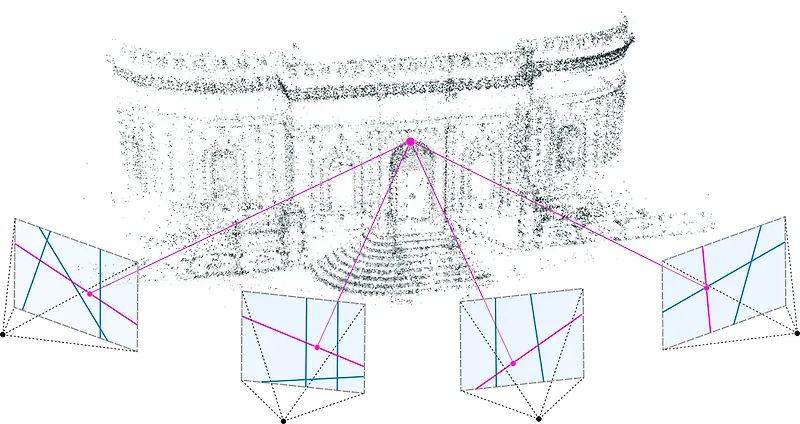
3DGS Method
특징
-
Sparse set of SfM(Structure from Motion) points가 input으로 들어간다.
-
Explicit scene representation
→ Optimization of 3D Gaussian position, opacity, covariance, SH 계수
→ 가우시안을 구성하는 파라미터가 explicit하게 설계되어 GT와 비교하여 최적화시킨다. -
Tile-based Rasterization
→ Parallel execution of kernels in CUDA & Differentiable Volumetric Representation
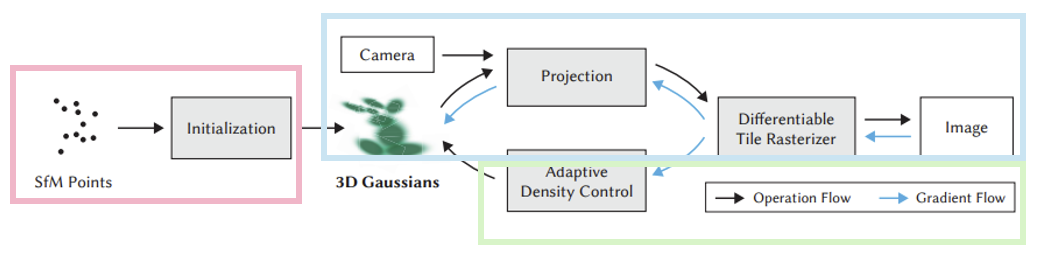
-
Initialization: COLMAP과 같은 SfM 알고리즘으로 camera pose와 point cloud 정보를 얻는다. 이때 얻은 point cloud가 3D Gaussian의 초기값으로 사용된다.
-
Projection: 3D Gaussian이 Image plane으로 projection되어 2D Gaussian 형태가 된다. 이 과정은 GT 이미지와 비교하여 파라미터를 update하기 위해 필요하다.
-
Differentiable Tile Rasterizer: 2D Gaussian을 하나의 이미지로 생성한다.
-
Gradient Flow: 생성된 이미지와 GT 이미지 간의 loss를 계산하고, loss만큼 gradient를 전파한다.
-
Adaptive Density Control: Gradient를 기반으로 Gaussian의 형태를 변화시킨다.

Psuedo code를 보면 크게 Initialization, Rasterization, Optimization, Densification 과정으로 나뉜다.
-
Initialization: 파라미터 초기화하는 부분
-
Rasterization & Optimization: 가우시안 구성하는 전체 파라미터 최적화한다. Inference 결과와 GT를 비교하여 loss를 계산하여 update한다.
-
Densification: 특정 iteration마다 수행되며, 가우시안을 remove, clone, split 하면서 개수를 변화시키고, 큰 구조를 변화시킨다.
Initialization
가우시안을 구성하는 파라미터들이 정의된다.
M, S, C, A가 있다.

: the center point of initial gaussian = mean
타원의 중심점이다. SfM으로 만든 point cloud로 초기화된다.
: covariance of gaussian = symmetric matrix
공분산으로, 대칭 행렬로 정의된다.
이때, 대칭행렬로 정의되는 이유는 Transpose가 곱해진 공분산 행렬의 성질 때문이다.
Pseudo code에서는 S로 표기 돼 있는데, 수식에서는 으로 표기 된다.
공분산은 R, S로 정의된다.
-
R: Rotation matrix
가우시안이 얼마나 기울어져 있는지 나타낸다.
: 4x1 quaternion vector to 3x3 rotation matrix
→ quaternion 표기법으로 하면 4개의 변수로 정의되는데, 학습 과정에서 최적화되며 quaternion 값이 3x3 rotation matrix로 변환되어 사용된다. -
S: Scale matrix
가우시안의 크기를 나타낸다.
: 3x1 scale vector to 3x3 scale matrix
: alpha of gaussian = opacity of gaussian = a real number
투명도를 나타낸다.
α-blending이란??
여러 이미지들을 합성할 때, 투명도(α)값을 사용하여 부드럽게 혼합하는 기술이다.
α 값이 작을수록 투명하고, α 값이 클수록 불투명하다.
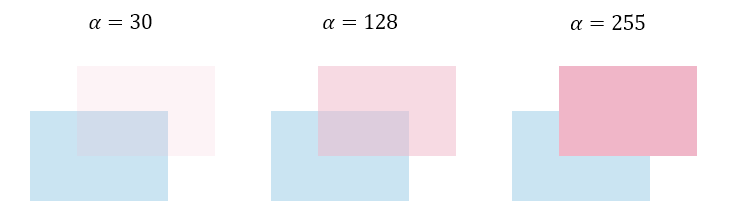
원래 이미지는 RGB 3가지로 표현되지만, 이미지에 투명한 효과를 주거나 이미지를 합성할 때 각 픽셀의 가중치를 제어하기 위해 RGB에 α를 추가하여 RGBA 4가지로 표현한다. α를 추가하여 투명도를 표현할 수 있게 된다.
: color of gaussian
Spherical Harmonic function으로 표현된다.
Spherical Harmonic function ?
구면 좌표계(Spherical coordinate system)로 color를 표현하는 함수이다. 구의 표면에서 정의된다.
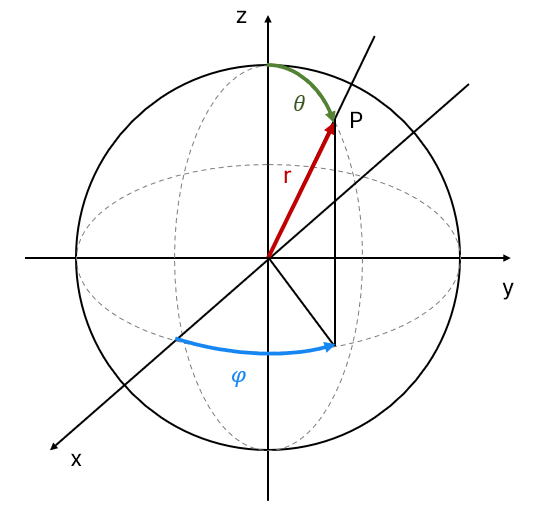
Camera Pose ()가 입력으로 들어가서 구의 표면 위치 P의 값을 출력한다.
수식에 대입하면 다양한 SH 값들이 정의된다.
-
: polar angle
-
: azimuthal angle
-
: SH 함수의 차수를 나타낸다.
- 함수의 공간적 복잡성 결정
- 작을수록 단순하고, 클수록 복잡하다.
- 정수 단위로 증가한다.
-
: 주어진 차수 에서 가능한 모든 방위 순서를 나타낸다.
- 함수의 대칭성과 관련 있다.
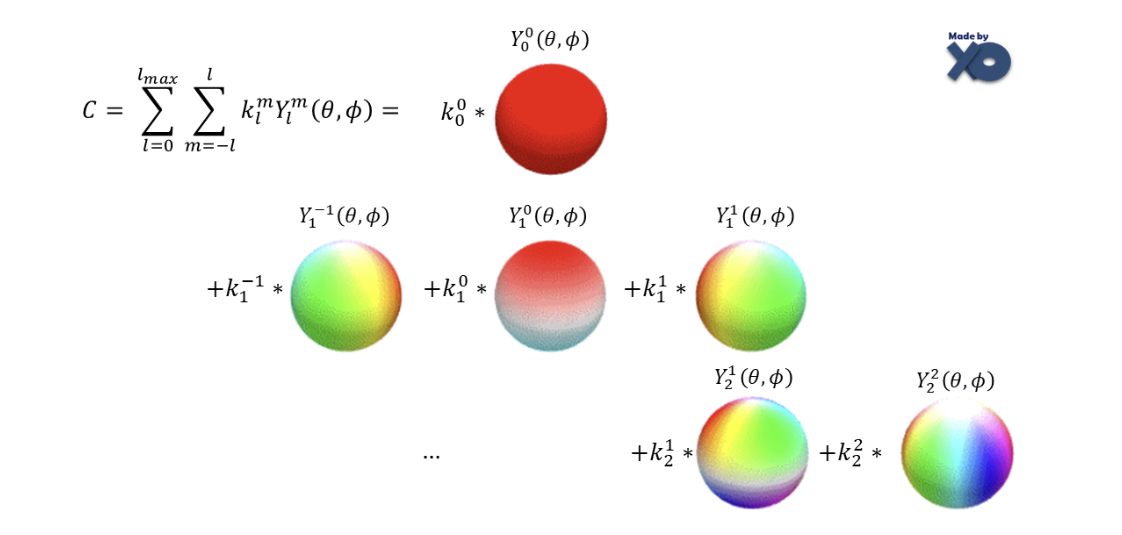
각 구를 쉽게 컬러 팔레트라고 생각하면 된다.
위 수식에서 는 최종적으로 계산되는 컬러이다.
Input은 view direction 값인 ()이고, output은 이다.
첫번째 는 에 대해 summation이 되고, 두번째는 m에 대해 계산된다.
값은 정답 컬러와 비교해서 최적화되는 파라미터이다. 팔레트 각각에 가중치 를 줘서 weighted sum한다.
정리하자면, 함수 Y라는 색상 팔레트에 대해 서로 다른 가중치를 매긴 값을 조합하여 최종 한 가지 색상 C를 만들어 낸다고 할 수 있다.
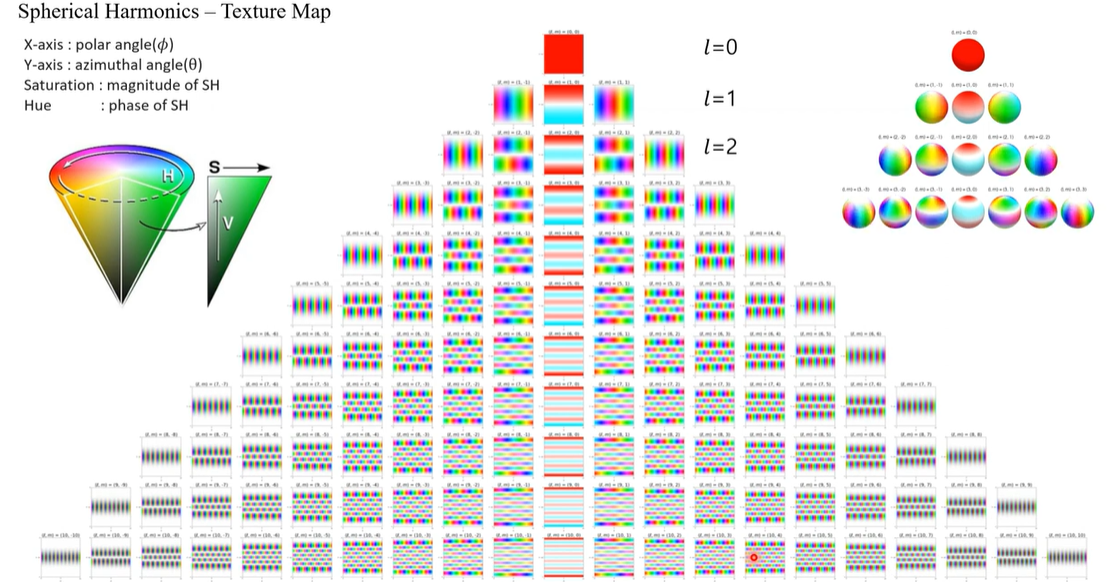
(SH 차수)이 증가할 수록 high frequency feature를 가진다. 더 복잡해진다는 것을 확인할 수 있다.
이제 파라미터 정의가 다 끝났다~ 3D Gaussian을 구성하는 파라미터는 position(M), covariance(S), color(C), Opacity(A)로 네 가지가 있다는 것을 알 수 있다.
Rasterization

Rasterization & Optimization 단계는 가우시안을 구성하는 파라미터를 최적화하고, 이미지를 렌더링하고, 렌더링된 이미지와 GT 이미지 간 loss를 계산하여 update하는 과정이다.
Sample Training View, Rasterize, Loss, Adam 단계로 구성된다.
Sample Training View
Input 데이터를 읽는 단계이다.
- Input: V(View Direction), I(GT 2D 이미지)
Rasterize
Tile-based rasterizer를 사용한다. View direction에 따라 M, S, C, A로 모델링된 가우시안을 2D 이미지로 렌더링한다. 중요한 단계임 !
- Input
- M (Mean = xyz)
- S (Covariance)
- C (Color)
- A (Opacity)
- V (View Direction)
- Output: I (2D 이미지)

Frustum Culling: 카메라 시야 밖의 Gaussian을 제거
Transform: 3D 공간의 Gaussian을 2D 스크린 공간으로 변환
Create Tiles: 이미지 좌표를 타일(Tile) 단위로 나눔
Duplicate With Keys: 각 타일마다 Gaussian의 Key(Depth 값 등)를 생성
Sort By Keys: Gaussian을 Depth 기준으로 정렬 (Radix Sort 활용)
Identify Tile Ranges: 각 타일별로 Gaussian 리스트 구성
Get Tile Range: 병렬 처리 시 Gaussian 데이터를 효율적으로 로딩 및 공유
Blend In Order: Depth 가까운 순서대로 색상(Color)과 알파(Opacity) 값 축적🤔❓ 이때, Tile-based rasterizer가 무엇일까 ?0?
단계별로 설명해보자면 . .
1. Cull Gaussian: Frustum culling
먼저 카메라의 frustum을 벗어나는 부분의 가우시안은 제거한다.
시야 벗어나는 가우시안은 제거한다고 이해했다. 이로써 불필요한 가우시안은 제거돼서 연산 비용을 줄일 수 있다.
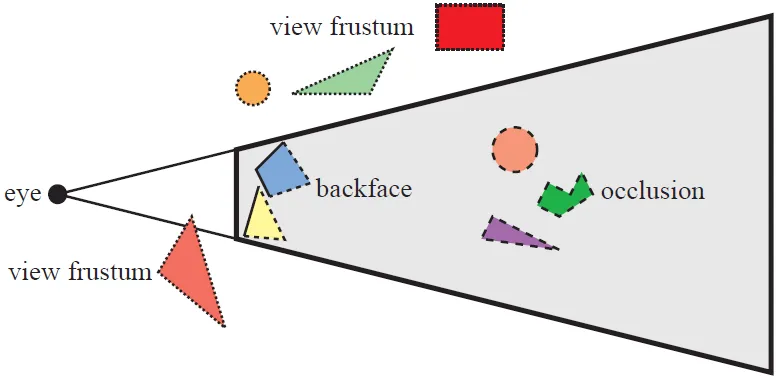
2. Screen Space Gaussian: 3D to 2D projection
이제 불필요한 3D 가우시안이 제거됐으니, 2D로 projection 해야 한다.
이때 3D 가우시안을 카메라 위치에서 1만큼 떨어진 2D image plane으로 projection한다.

변환 과정은 <World 좌표계 (3D) → Camera 좌표계 (3D) → 2D 이미지> 이다.
3D 가우시안이 2D로 projection되는 수식이다.
Transpose는 공분산의 성질인 대칭 행렬을 만들기 위해 곱해진다.
-
: Jacobian 행렬
-
Camera 좌표계에서 2D 이미지 좌표로 변환될 때 사용되는 미분 행렬이다.
-
원래 3D 좌표 에서 2D 좌표 로 사영(projection)할 때, 선형 변환이 아니라 비선형적인 변환이 일어난다.
-
이를 해결하기 위해 미분을 사용한 근사(linear approximation) 를 수행하는데, 이때 사용되는 행렬이 Jacobian 행렬이다.
-
는 3D 좌표에서 2D 이미지 좌표로 변환될 때의 변화율을 포함하며, 대략적으로 아래 형태를 가진다.
- 즉, 는 비선형 변환을 국소적으로 선형 변환처럼 다룰 수 있도록 도와주는 행렬이다.
-
-
: world 좌표계 → camera 좌표계 변환 행렬
-
Camera 내부에서 보는 좌표계로 변환하는 과정에서 사용되는 회전(R) + 이동(T) 변환 행렬이다.
-
Homogeneous coordinates를 사용하면, 일반적으로 아래와 같은 형태로 표현된다.
여기서 은 3×3 회전 행렬, 는 3×1 이동 벡터이다.
-
3. Create Tiles: split the screen into 16x16 pixel tiles
병렬 처리를 위해 나눠준다.

4. Duplicate with Keys: generate keys of each gaussian every tile
타일마다 각 2D 가우시안에 key를 할당한다.
key = depth + ID
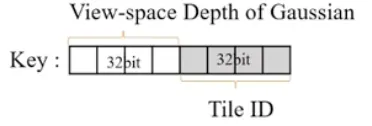
카메라 포즈값 기준으로 depth를 넣어준다. Tile ID는 타일 번호이다.
5. Sorted by Keys: depth ordering by Radix Sort each tile
앞 과정에서 할당한 key로 가우시안을 sorting한다.
타일마다 존재하는 가우시안들을 depth 값을 기준으로 정렬하는 과정이다. 각 타일 내에서 가까운 가우시안부터 차례로 처리할 수 있도록 한다.
6. Identify Tile Ranges: identify Gaussians list each tile
앞 과정에서 가우시안들을 깊이 순서대로 정렬했다. 이제 depth-sorted된 가우시안으로 가우시안 리스트를 생성한다.
각 타일마다 가우시안의 리스트가 구성되었다.
7. Get Tile Range: read Gaussian list
모든 타일에서 range를 불러온다
- 병렬처리할 때 데이터를 loading, sharing
- forward/backward processing
을 효율적으로 할 수 있게
8. Blend in Order
Depth 순서대로 색상과 투명도 값을 축적하면서 최종 이미지를 생성하는 단계이다.
Accumulates color and values by traversing the lists front=to-back each pixel.
When a target saturation of in a pixel, the corresponding thread stops.
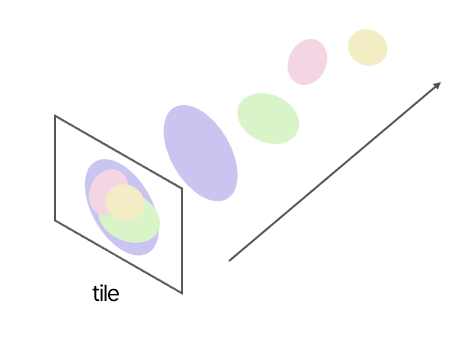
타일 별로 thread block를 실행한다. 각 타일을 병렬적으로 처리하기 위해 thread block을 할당한다.
그 후, 가까운 가우시안부터 순차적으로 색상, 투명도 값을 누적하여 가우시안을 blending한다.
값이 saturation에 도달하면 중지하고, alpha compositing을 적용하여 앞쪽 가우시안의 투명도 비율을 고려하여 색상을 혼합한다.
타일 단위로 병렬 처리하기 때문에 빨리 렌더링할 수 있다!
+backward process
propagate gradients following the ratio of the opacity of gaussian
가우시안의 opacity 비율에 따라 gradient(기울기)를 전달하는 과정이다. Opacity를 기준으로 하는 이유는 최종 이미지에 큰 영향 주는 가우시안을 중심으로 학습하기 위해서라고 이해했다.
- 가우시안의 opacity 비율이 클수록 gradient를 더 많이 전달한다. (불투명한 가우시안일수록 이미지에 더 큰 영향 주니까 중요하다.)
- Depth가 먼 가우시안은 gradient가 적게 전달된다.
- Depth가 가까운 가우시안일수록 최적화해서 중요한 역할을 수행한다.
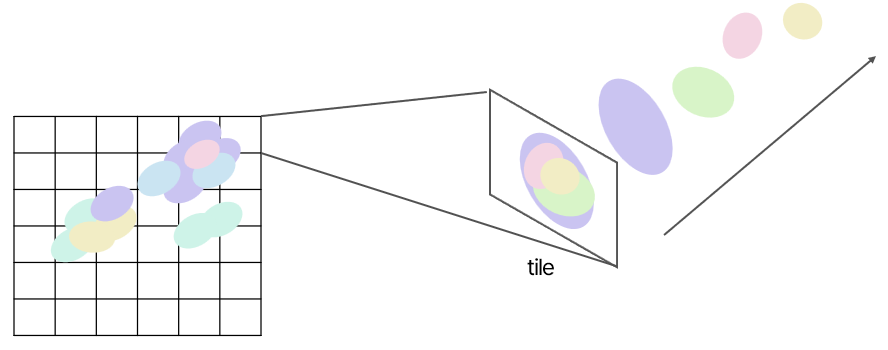
요론 느낌.. (귀찮아서 16x16으로 안그림)
각 Tile이 병렬적으로 가우시안들을 처리하고, 픽셀 단위에서 depth 순서대로 blending이 이루어진당
Loss
GT 이미지와 Inference 이미지 사이의 차이를 계산한다.
Adam
가우시안을 구성하는 4가지 파라미터는 Adam optimizer로 update 된다.
Densification
→ Adaptive control of gaussians

Densification은 특정 iteration마다 수행되며, 가우시안을 제거하거나 복제하거나 쪼개서 수를 변화시킨다.
100 iteration마다 한번씩 실행되며, 특정 threshold보다 투명도()가 작으면 가우시안이 제거된다. 논문에서는 threshold가 0.005로 설정되었다. 너무 작은 opacity의 가우시안은 최종 이미지에 영향을 거의 주지 않기 때문이다. 이렇게 가우시안 개수를 줄이면서 정리한다.
또한, position threshold가 0.0002보다 크면 가우시안이 scene을 제대로 모델링하지 못했다고 판단하고 가우시안을 split하거나 clone한다.
특정 scale threshold보다 크면 split하고, 작으면 clone한다. 너무 크게 확장된 경우, 하나의 가우시안을 2개로 나누고 크기를 1.6배 감소시킨다.
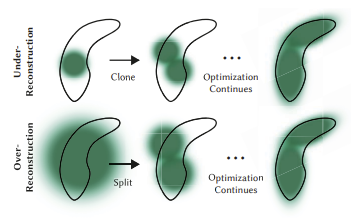
검정 선은 GT 이미지의 경계로, loss를 줄이기 위해 검정 선을 기준으로 reconstruction한다.
Under-reconstruction, over-reconstruction을 remove, split, clone을 통해 해결한다.
Isotropy vs. Anisotropy
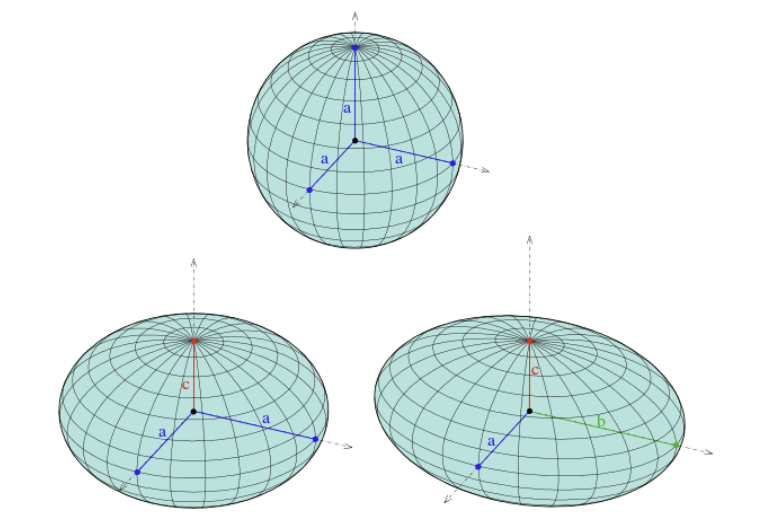
Isotropic는 방향에 따라 변하지 않는 특성이고, Anisotropic은 방향에 따라 다르게 보이는 특성이다.
Isotropic gaussian은 방향에 상관없이 반지름이 같은 3차원 구라고 할 수 있고, Anisotropic gaussian은 구 아래에 입체 타원..?처럼 방향에 따라 다른 반지름 갖는 형태라 할 수 있다.
Anisotropy 일 때 렌더링 퀄리티가 더 좋다.
