Camera Calibration

chaenyang·2025년 1월 17일

Camera Camera Calibration

self-driving

목록 보기

7/9

Preliminary

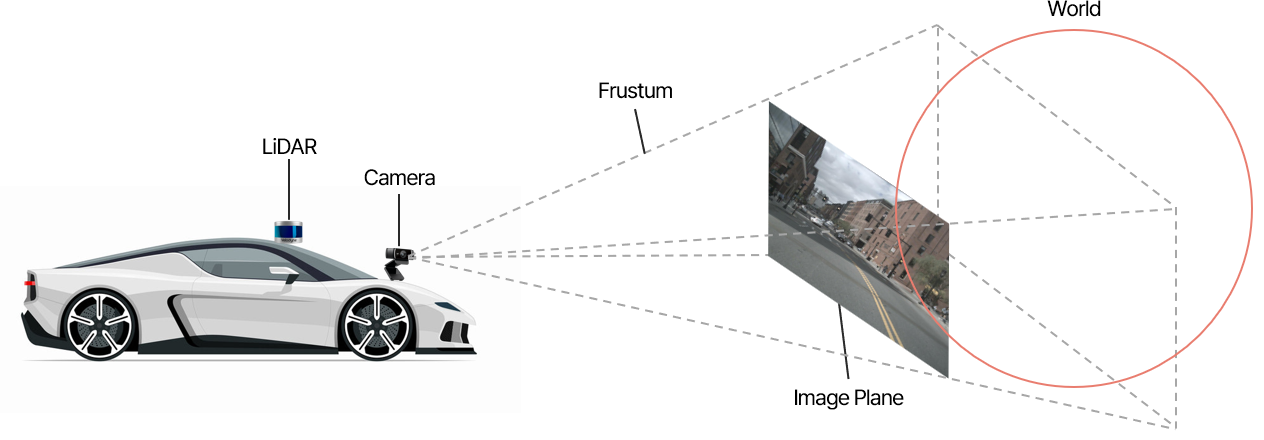
세상은 3차원인데 카메라나 우리 눈은 2차원 평면으로 보이게 만든다.

카메라 움직일 때 화면이 달라지는 이유는 Camera Extrinsics가 변하기 때문이다.

zoom in/out 할 때 화면이 달라지는 이유는 Camera Intrinsics가 변하기 때문이다.

오이현상이 발생하는 이유는 Camera Distortion이 존재하기 때문이다.

→ Camera Extrinsics, Intrinsics, Distortion 정보를 모두 알고 있다면 카메라가 세상을 2차원으로 만드는 것을 그대로 구현할 수 있다.

→ 3가지 정보를 잘 조작하여 원하는 방식대로 3차원 세상을 2차원으로 만드는 것이 가능하다.

STEP

STEP 1. 월드 좌표계 설정

3차원 세상에서 임의의 점을 잡고 원점으로 설정하면, 모든 물체의 위치를 좌표로 나타낼 수 있다.

임의로 원점을 잡는 것을 월드 좌표계를 설정한다고 한다.

STEP 2. 월드 좌표계의 위치좌표를 카메라 좌표계의 위치좌표로 변환

화면에 세상을 담기 위해서는 우선 카메라가 세상을 어떤 시야로 보고 있는지 알아야 한다.

카메라의 시야에서 세상을 바라보고 있으므로, 월드 좌표계를 카메라 좌표계로 변환한다.

월드 좌표계 기준의 위치좌표에 Camera Extrinsics 행렬을 곱하면 카메라 좌표계 기준의 위치좌표로 변환된다.

즉, Camera Extrinsics는 카메라의 위치 및 바라보는 방향 등의 카메라의 외부 정보를 담고 있다.

Step 3. 카메라 좌표계의 위치좌표를 픽셀 좌표계의 위치좌표로 변환

카메라의 위치가 고정돼 있어도 카메라 내부의 설정에 따라 보이는 것이 달라진다.

카메라 좌표계에 Camera Intrinsics 행렬을 곱하면 픽셀 좌표계로 변환된다.

즉, Camera Intrinsics는 카메라의 초점거리, 주점의 위치 등 카메라 내부 정보를 담고 있다.

→ 이 과정들을 통해 3차원 세상(월드 좌표계의 위치좌표)이 2차원 화면(픽셀좌표계의 위치좌표)으로 매핑된다.

Concepts

1. Camera Extrinsics

P = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ 0 & 0 & 0 & 1 \end{bmatrix}

Camera Extrinsics는 2가지 정보, 카메라가 바라보는 방향과 카메라의 위치를 가지고 있는 행렬이다.

계산의 편의성을 위해 homogeneous coordinate를 활용한다.

$R \in \mathbb{R}^{3\times3}$ 은 카메라의 회전 정보(x, y, z축)를 모두 담고 있는 행렬이다.
t\in \mathbb{R}^{3\times1}는 카메라의 위치 정보를 담고 있는 행렬이다.

Homogeneous Coordinate란?

(x, y)를 (x, y, 1)로 표현하는 것이다.

Homogeneous 좌표계를 사용하면 Affine 변환이나 perspective(projective) 변환을 하나의 행렬로 표현할 수 있다.

Affine 변환은 회전, 평행이동, 스케일 뿐만 아니라 shearing, 반전(reflection)까지를 포함한 변환이다.

\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix} + \begin{bmatrix} e \\ f \\ \end{bmatrix}

\begin{bmatrix} x' \\ y' \\ 1 \\ \end{bmatrix} = \begin{bmatrix} a & b & e\\ c & d & f \\ 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}

장점은..
- 복합 변환의 효율성과 일관성을 높임 → 미리 곱해 하나의 행렬로 변환해놓기 가능
- 코드의 간결성과 유지보수성을 개선함 → 코드 짧아짐
- GPU 가속을 통한 계산 효율성 향상에도 기여함 → 행렬곱만으로 변환을 구성하기 때문

2. Camera Intrinsics

K = \begin{bmatrix} f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}

Camera Intrinsics는 3가지 정보, 초점거리, 주점의 위치, 비대칭 계수를 가지고 있는 행렬이다.

$f_x$ : x축 초점거리
$f_y$ : y축 초점거리
$(c_x, c_y)$ : 주점의 위치
$s$ : 비대칭 계수

3. Camera Distortion

렌즈 특성상 발생하는 이미지의 왜곡이다.

Radial Distortion, Tangential Distortion이 있다.

1. Radial Distortion (방사 왜곡)

이미지의 중심에서 멀어질수록 커지는 왜곡으로, 넓은 시야를 가진 광각 렌즈에서 특히 두드러진다.

x_{distorted} = x(1 + k_1r^2 + k_2r^4 + k_3r^6)

y_{distorted} = y(1 + k_1r^2 + k_2r^4 + k_3r^6)

$(x, y)$ : 왜곡 전 좌표
$(x_{distorted}, y_{distorted})$ : 왜곡된 좌표
$r = \sqrt{x^2 + y^2}$
$k_1, k_2, k_3$ 는 방사 왜곡 계수로, 각각 2차, 4차, 6차 방사왜곡을 설명한다. 보통 $k_1$ 과 $k_2$ 만 사용하며, $k_3$ 는 무시되기도 한다.

2. Tangential Distortion (접선 왜곡)

렌즈와 이미지 센서가 완전히 평행하지 않을 때 발생하는 왜곡이다.

x_{distorted} = x + [2p_1xy + p_2(r^2 + 2x^2)]

y_{distorted} = y + [p_1(r^2 + 2y^2) + 2p_2xy)]

$p_1, p_2$ 는 접선 왜곡 계수이다.

왜곡 계수란 . . ?

카메라 왜곡을 보정하기 위해 왜곡 계수 d를 다음과 같이 정의한다.

d = [k_1 \, k_2 \, p_1 \, p_2 \,k_3]

OpenCV와 같은 카메라 보정 라이브러리에서 사용되며, camera calibration 과정에서 얻어진 값을 통해 방사 및 접선 왜곡을 보정할 수 있다.

Camera Calibration

개념

카메라의 외부 파라미터(Camera Extrinsics)와 내부 파라미터(Camera Intrinsics)를 정확히 계산하는 것이다.

3D 공간에 있는 물체의 좌표와 이를 촬영한 이미지 상의 2D 좌표를 이용한다.

필요한 이유

3차원 세상이 2차원 평면(이미지 센서)에 어떻게 매핑되고 있는지 확인하기 위해 필요하다.

2D 좌표만으로 3D 깊이를 파악할 수 있다.

자율주행에서 매순간 Camera Extrinsics와 Camera Intrinsics가 달라지게 된다.

준비물

준비물: 체커보드, 카메라, OpenCV

체커보드를 사용하는 이유는 3D 좌표를 설정하기 편하고 2D 좌표 인식의 정확성 때문이다.

체커보드의 특징

Gradient Change
- 체커보드는 검은색과 흰색 사각형으로 구성돼 있다.
- 두 색 사이의 경계에서 픽셀 값이 급격하게 변하기 때문에 이미지에서 기울기 변화가 뚜렷하게 나타난다.
  - 흰색 픽셀 값: 255
  - 검은색 픽셀 값: 0
  - 이 경계에서는 픽셀 값이 급격히 변화하기 때문에 경계 감지 알고리즘이 쉽게 해당 위치를 찾을 수 있다.
교차점 구조의 규칙성
- 체커보드는 정렬된 격자 형태로 구성된다.
- 각 사각형의 모서리 교차점은 서로 일정한 간격을 갖기 때문에, 알고리즘이 이를 체계적으로 탐지할 수 있다.
특이한 패턴으로 인해 잘못 탐지할 가능성 감소
- 체커보드의 모서리 패턴은 매우 독특하다.
- 다른 물체나 배경 요소가 체커보드처럼 보일 가능성이 낮기 때문에, 교차점을 정확히 감지할 확률이 높아진다.