[GGP] 11. Screen-space Object Manipulation

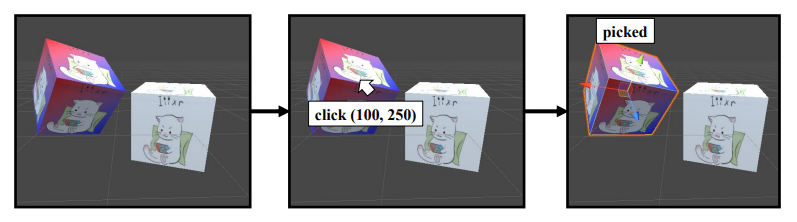
☁️ Object Picking

🔎 Picking

touch screen을 손가락으로 누를 때 object가 선택되는 과정을 의미한다.

• 클릭한 좌표
  = screen space 좌표
  = 2D pixel coordinate $(x_s, y_s)$
  

🔎 Ray-object intersection

• 클릭을 하면 z 축 방향으로 ray(screen space에서 정의)를 쏴서 가장 가까운 object를 선택
• 이때 object와 부딪히는 지 확인하려면 screen space에서 object space까지 거슬러 올라가야함. 이전의 space들에서는 개별 object에 대한 정보를 가지고 있지 않기 때문..
• screen space -> clip space -> camera space -> world space -> object space
  
  
  

전체적인 흐름
1. camera space ray의 시작점을 $(x_c,y_c,n)$로 둔다.
2. projection transform = clip space 좌표를 얻는다.
3. viewport transform = screen space 좌표를 얻는다.
4. 3에서 구한 결과와 우리가 클릭한 좌표 $(x_s,y_s,0)$가 같음을 이용하여
camera space 좌표 $(x_c,y_c,n)$을 구한다.
5. $(x_c,y_c,n)$를 이용해서 direction vector(ray)를 계산한다. = $(x_c,y_c,n)$ - 원점
6. Inverse view transform, world transform을 통해서 ray를 각 object space로 가져온다.
7. BV나 Ray-Triangle Intersection을 통해 오브젝트와의 충돌을 감지한다.

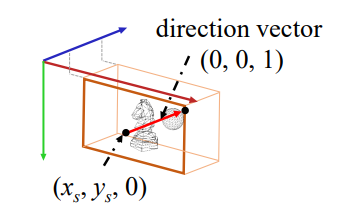
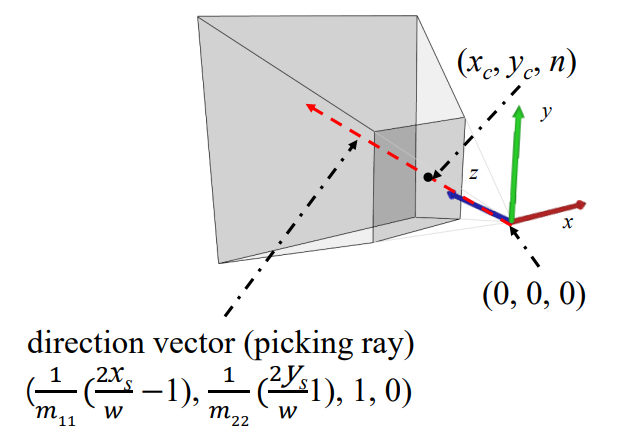
☁️ Camera-space Ray

🔎 Ray in the camera-space

• camera space ray의 시작점 : $(x_c,y_c,n)$
  = near plane 위의 점
  

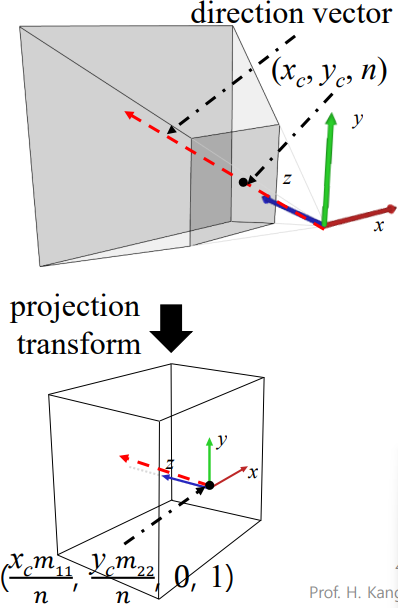
1. projection matrix를 통해 projection transform 진행
   = 결과로 clip space 좌표를 얻는다.
   
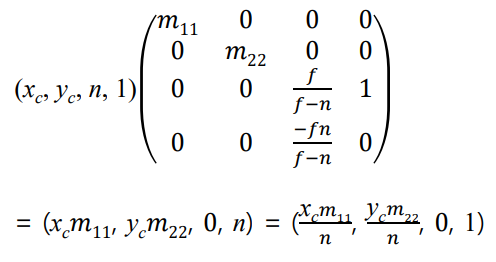
2. viewport matrix를 곱해서 screen-space transform
   
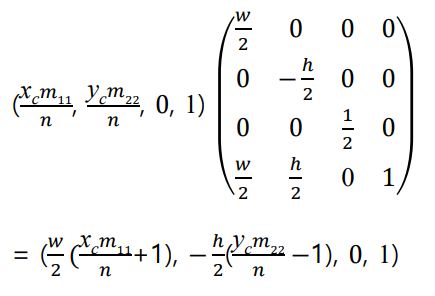
3. 2에서 구한 결과와 우리가 클릭한 좌표 $(x_s,y_s,0)$가 같아야 한다.
   
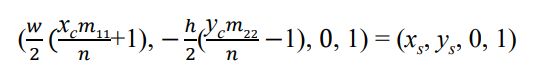
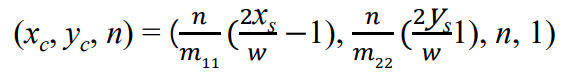
4. $(x_c,y_c,n)$를 이용해서 direction vector를 계산한다.
   direction vector = camera space 시작지점 - 원점
   

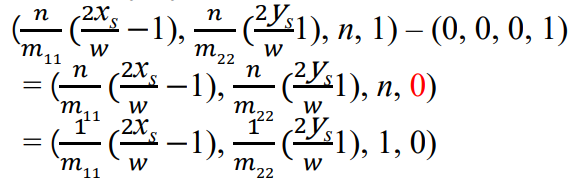
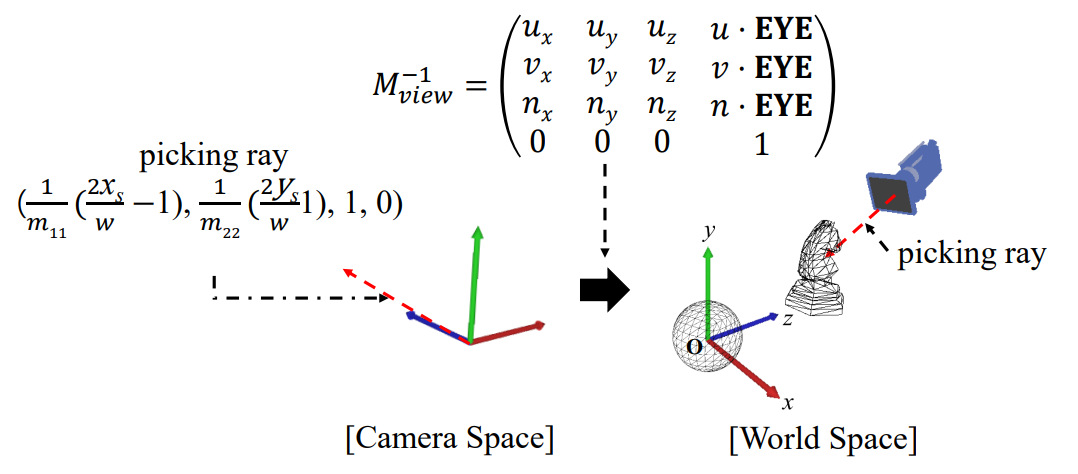
☁️ World-space Ray

🔎 Camera-space ray to the object-space ray

= inverse of view transform

• Mview = TR
• T는 -EYE로 translation 되지만 T-1는 EYE로 translation
  
• picking ray = 앞에서 구한 것
  

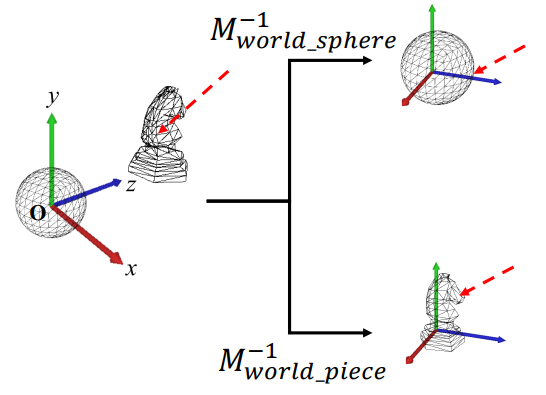
☁️ Object-space Ray

🔎 Intersection per object

• 물체 각각의 object space로 날아간다.
• 각 물체가 ray와 충돌했는지 알기위해서는 ray-triangle intersection test가 필요
• 하지만 더 빠른 방식인 vounding volume (BV)를 이용할 것이다.
  

☁️ Bounding Volumes (BV)

= BV는 물체를 감싸는 간단한 geometry이다.
= BV를 기준으로 ray 충돌 여부를 체크한다 -> cost가 줄어든다

• AABB (Axis aligned bounding box)
  x , y , z축 위에 범위 설정
• bounding sphere
  중심까지의 거리로 판단

🔎 Ray equation

• bounding sphere equation을 통해 ray와 sphere의 교점을 구한다.
  
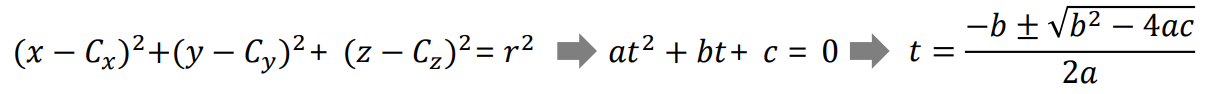
• 해의 개수로 ray와 충돌했는지 판단
  
• 이후 정밀한 결과가 필요하면 ray-triangle intersection test나 multiple bounding volume test를 한다.

☁️ Ray-Triangle Intersection

= BV보다 정밀한 체크가 가능하다.
= 무게중심 좌표(barycentric coordinate)를 이용한다.

• triangle <a, b, c> is hit by a ray at p
• p를 기준으로 3개의 sub-triangle로 나눠진다.

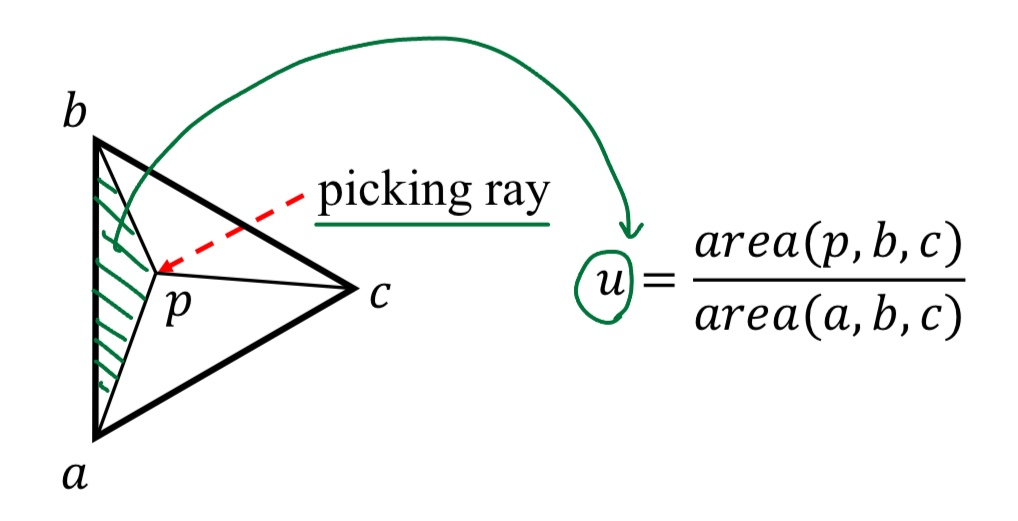
• $u,v,w$는 sub triangle들의 넓이비
  
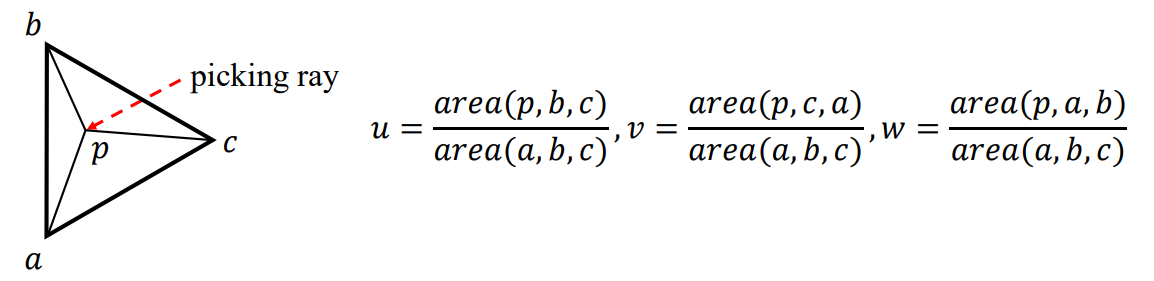
• $u+v+w = 1$ , Cramer's rule을 이용해서 식을 정리한다
  
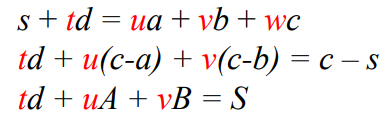
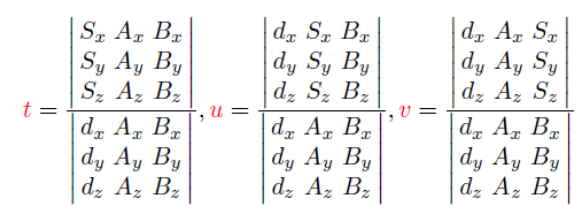
• $u,v$ 값의 합으로 p의 위치를 판단한다.
  
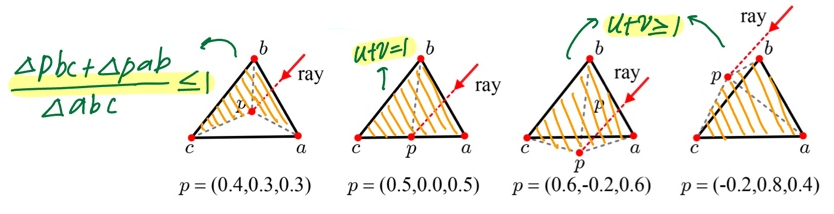
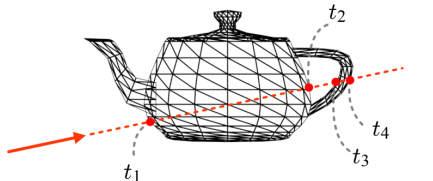
• multiple intersection인 경우 smallest positive t를 선택한다.
  

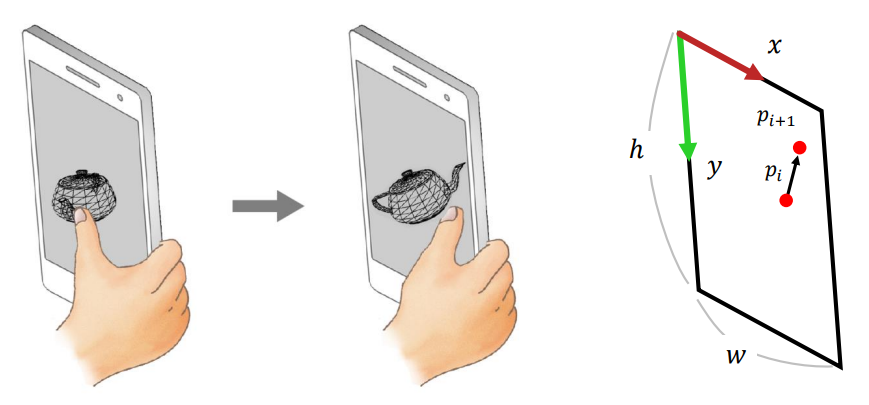
☁️ Rotating an object

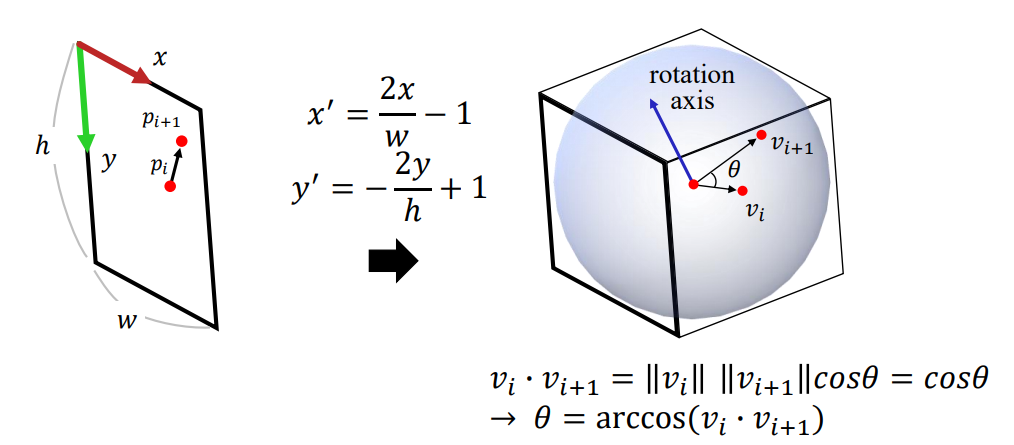
• pi 에서 pi+1로 sliding.
  

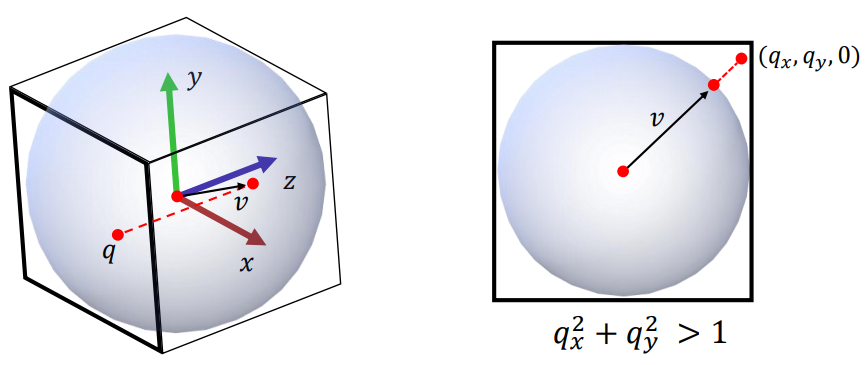
🔎 Arcball

= screen 뒤의 virtual ball
= unit sphere

• 2D screen은 2x2 square로 normalize 된다.
  
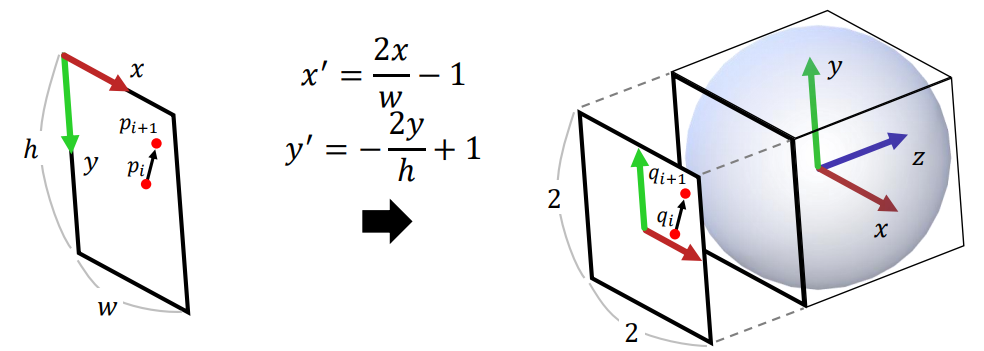
• 우리가 screen에서 클릭한 점 $q$는 arcball 위의 점 $v$으로 projection 된다.
• $v_x = q_x , v_y = q_y$
  
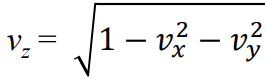
• rotation axis : 어느 축으로 회전을 할 것인가?
  = vi 와 vi+1의 cross product
• rotation angle : 얼마나 회전을 할 것인가?
  = vi 와 vi+1의 dot product
  

☁️ Object-space Rotation Axis

• 그럼 이 회전을 언제 적용함?
  • 월드 변환 전에 적용
  • 아크볼 공간은 랜더링 파이프에 원래 있던 공간이 아님 = 회전축을 마치 camera space에서 정의됐던 것 처럼 하자.. trick인 거임
  • 아크볼 공간에서 정의된 3차원 회전축을 카메라 space로 그대로 옮김
• arcball은 가상의 space(camera space)이기 때문에 object space로 보내줘야 한다.
• object space에서 world space로 바꾸는 world transform을 할 때 rotation 과 transition이 일어나기 때문에 world transform 전에 먼저 회전을 적용시켜야 한다.