오늘 살펴볼 내용의 비유 ver. [이미지 출처]: 하용호, 자습해도 모르겠던 딥러닝, 머리속에 인스톨 시켜드립니다.

Batch Size

1) Stochastic Gradient Descent

각 반복(iteration)마다 단일 데이터 샘플을 사용하여 파라미터를 업데이트한다.

• 특징
  • 매 반복마다 빠른 업데이트가 가능하지만, 각 업데이트가 노이즈에 민감하다. 따라서 훈련 데이터 샘플에 의해 크게 변동하므로 최적화 과정이 불안정할 수 있다.
  • 그러나 매우 큰 데이터 세트에서 빠르게 최적화를 수행하고자 할 때 유용합니다.
    
    
    

2) Mini-batch Gradient Descent

가장 많이 사용되는 방법이다. 각 반복마다 소규모 배치(batch)로 나눈 훈련 데이터 샘플을 사용하여 파라미터를 업데이트한다.

• mini batch size는 매우 중요하다.
  우리는 flat minimizer에 도달하는 것이 중요한데, 배치 사이즈가 너무 크면 sharp minimizer에 도달하게 된다. 즉, overfitting될 가능성이 크다는 것이다. 따라서 적당히, 128, 256개 정도의 mini batch size로 gradient 구하여 update할 필요가 있다.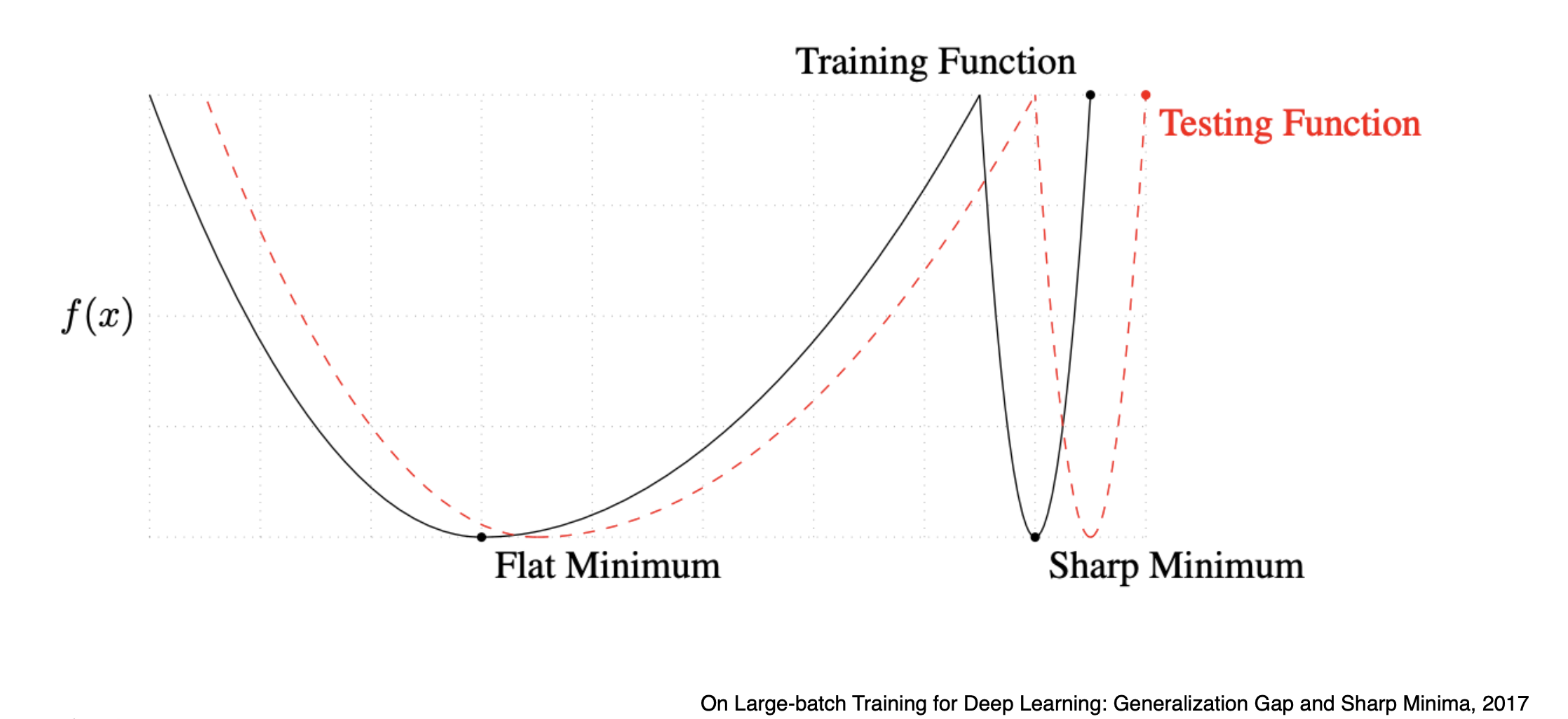

3) Batch Gradient Descent

각 반복마다 전체 훈련 데이터 세트를 사용하여 파라미터를 업데이트한다.

가장 안정적이지만 업데이트가 느리다는 단점이 있다. 따라서 데이터 세트가 작고, 메모리 제한이 없을 때 적합하다.

---

Gradient Descent 방법

1) Stochastic Gradient Descent

SGD는 Learning rate를 적절하게 잡는 것이 매우 어렵다는 문제가 있다.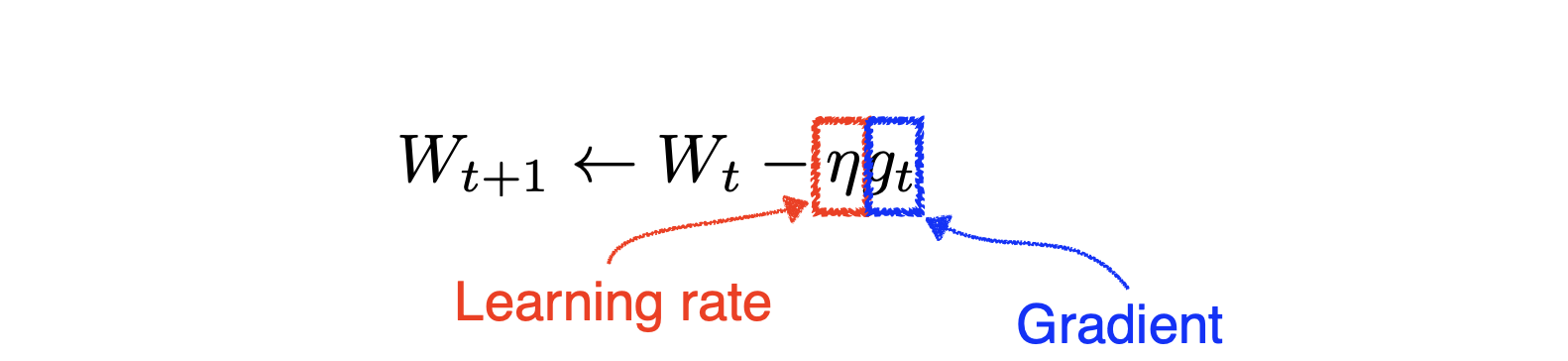

2) Momentum

모멘텀을 사용한다는 것이 가장 큰 특징이다. Momentum은 한번 흘러가기 시작한 gradient reduction 방향을 어느정도 유지시켜주며 gradient를 update한다. 즉, 이전 기울기(gradient)의 영향을 현재 기울기에 추가하여 관성 효과를 만듦으로써 경사하강법의 진동을 줄이고 수렴 속도를 높인다. 더불어 경사하강법이 깊은 골짜기에서 빠져나오도록 도와준다고 한다.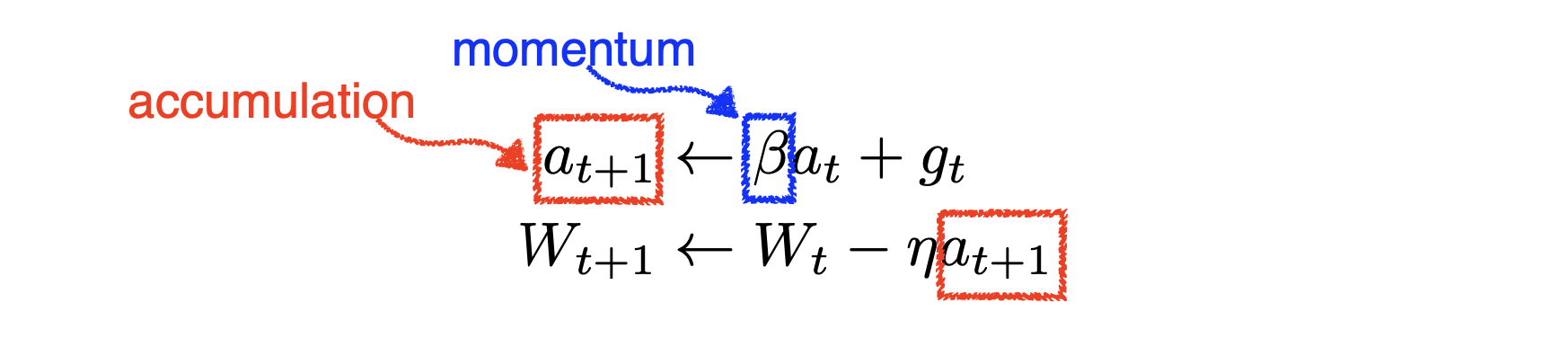

3) Nesterov Accelerated Gradient

4) Adagrad

Adagrad는 neural network의 파라미터가 얼마나 변화왔는지를 추가로 보게 된다. 이를 통해 많이 변한 파라미터에 대해서는 더 적게 변화시키고, 안 변한 파라미터는 더 많이 변화시켜본다. 즉, 파라미터 값을 계속 제곱으로 더해준다는 뜻인데, 그렇게 되면 G가 계속 커져서 결국 무한대로 가게 된다. 그런데 아래 식에서 알 수 있다시피, G는 분모에 있으므로 뒤로 갈수록 가중치 w가 업데이트가 되지 않고 학습이 점점 멈추는 문제가 발생한다. 이에 다음의 후속작들이 등장하였다.

(참고) 적게 변한 곳은 많이 변화시키게 하고, 많이 변화한 곳은 적게 변화하도록 하는 이유가 무엇일까?
적게 변한 곳 = Gradient가 작다 = 평평하다 = 평평한 곳은 많이 가도 얼마 바뀌지 않는다 = 빨리 가자!

경사를 보고 가파른 쪽은 좀 조심조심 가고, 완만한 쪽은 과감하게 가자!
출처: 혁펜하임 https://www.youtube.com/watch?v=-oHYAUhq5ao

5) Adadelta

AdaDelta는 AdaGrad의 $G_{t}$값이 계속 커지는 현상을 방지하기 위해서 고안되었다. 이를 위해 AdaDelta는 윈도우 방식을 이용한다. 윈도우 방식을 이용한다는 것은 현재로부터 기울기의 누적합을 윈도우 크기만큼만 고려한다는 뜻이다. 하지만, 이를 구현하기 위해선 윈도우 크기만큼의 공간을 할당해야한다. 이는 불필요한 메모리 낭비를 야기한다. 따라서, 원리는 윈도우 방식이 맞지만 지수 가중 평균(exponentially weighted average)을 이용한다.
출처: https://imlim0813.tistory.com/18

목적
Adagrad의 학습률 감소 문제를 해결하기 위해 사용된다.

개념
과거의 기울기 제곱 합 대신 지수적으로 가중치를 부여(지수가중평균, exponential window moving average)하여 학습률을 조정한다.

(참고) exponential window moving average란? 이전의 정보는 조금 잊어가면서 값을 업데이트하는 함수

(참고) $G_{t}$는 gradient를 제곱하여 더한 것이므로 gradient 그 자체(방향+크기)가 아니라 크기를 누적한 것이다.

특징
Adaelta의 특징은 learning rate를 조정하지 못한다는 것이다. 이것이 장점이 될 수도 있겠으나, Naver 강의에서는 우리가 조정할 수 있는 요소가 그만큼 적은 것이기 때문에 잘 사용하지 않는다고 하였다.

6) RMSprop

개념
지수 이동 평균을 사용하여 기울기의 제곱을 계산하고 학습률을 조정한다.

Adadelta와 유사하다. 다만 stepsize(learning rate)가 추가되었다는 점이 다르다! 다시 한 번 이야기하지만, $G_{t}$는 gradient를 제곱하여 더한 것이므로 gradient 그 자체(방향+크기)가 아니라 크기를 누적한 것이다.

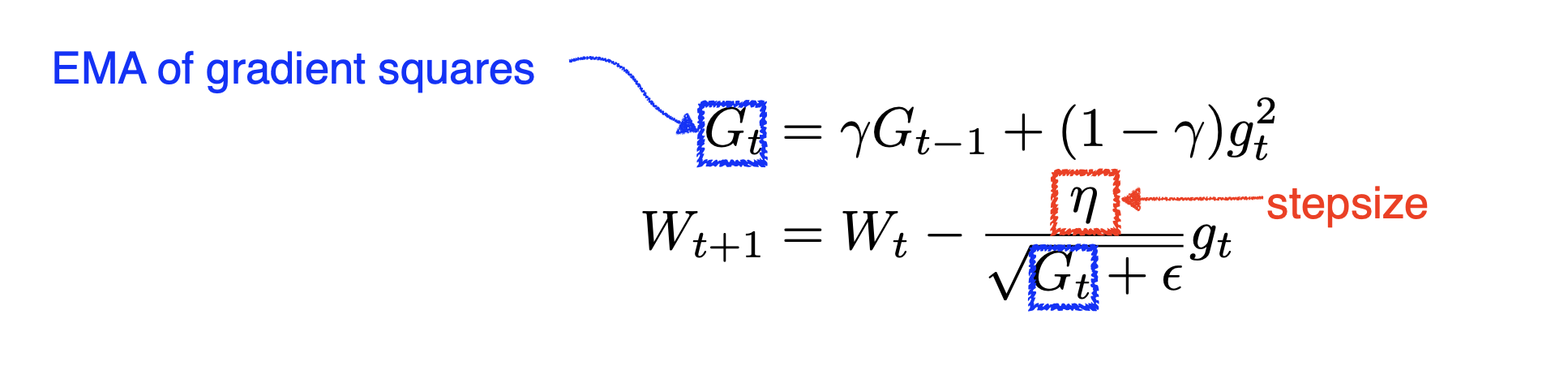
7) Adam

목적
모멘텀과 RMSprop을 결합하여 더 빠르고 안정적인 학습을 위해 사용된다.

개념
모멘텀을 사용하여 1차 모멘트(기울기)와 2차 모멘트(기울기의 제곱)를 추정하여 학습률을 조정한다.

위 식에서 알 수 있듯, 분자에 momentum이, 분모에 RMSProp이 들어간 식이다.
즉, 적게 탐색한 축으로는 많이 탐색하게끔, 많이 탐색한 축으로는 적게 탐색하게끔 함.
출처: 혁펜하임 https://www.youtube.com/watch?v=wVBuPlBBbAE

좀 더 practical한 level로 들어가서 이야기하자면 입실론 $\epsilon$ 숫자를 잘 바꿔주는 것이 매우 중요하다. 입실론은 전체 gradient descent가 unbiased estimator가 되도록 수학적으로 넣어준 값이지만, 이 값이 영향을 꽤나 주나보다!

Adam이 대부분 가장 좋은 성능을 보인다. 그러나 Adagrad나 RMSprop이 더 적합한 경우도 존재함!