
안녕하세요 첫번째 생성 심화 세미나 강의를 맡게된 투빅스 16기 김건우입니다. 오늘 주제는 생성 모델 중 기초이자 근본인 VAE (Variational Auto-Encoder)를 준비했습니다.
Introduction
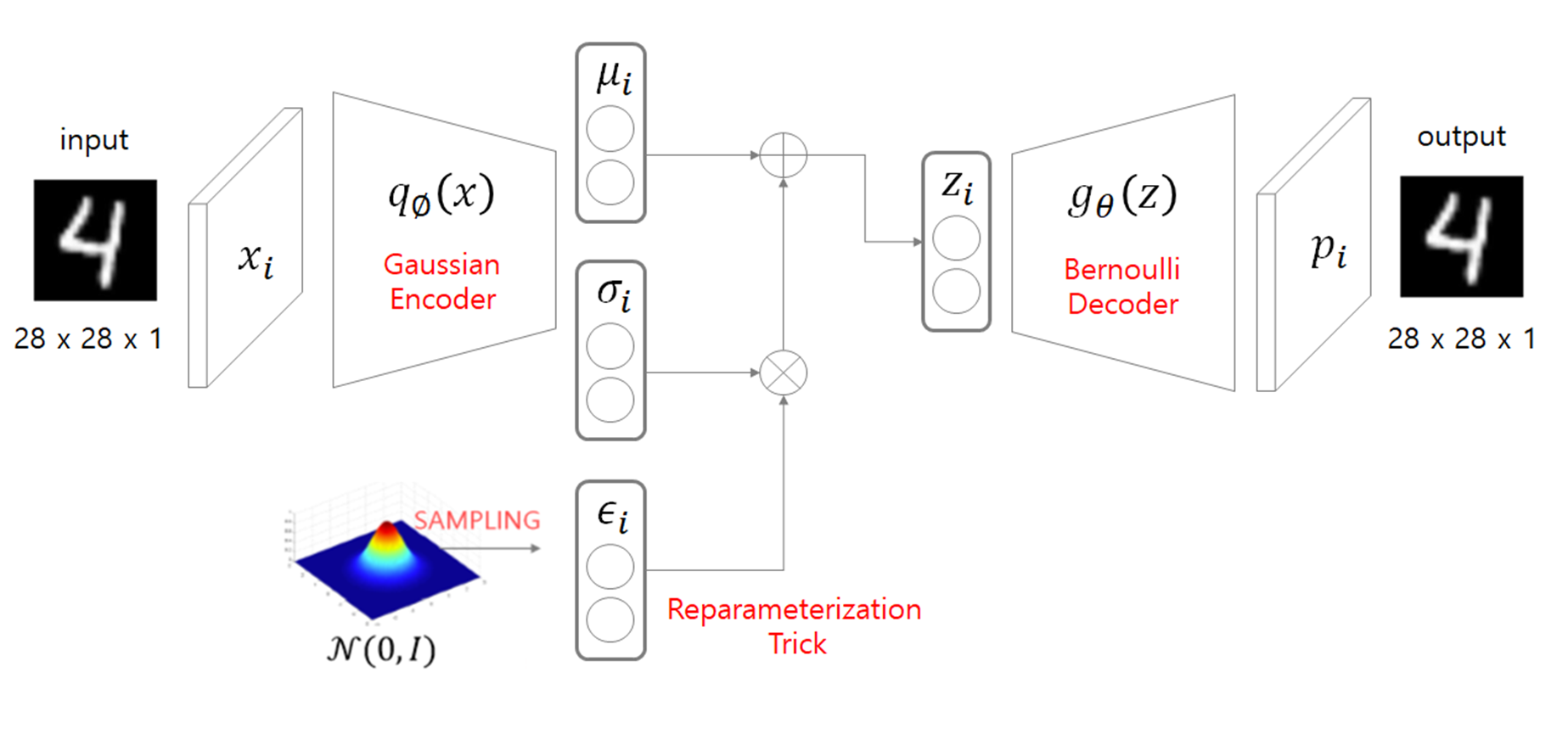
여기 보이는 그림은 VAE의 전반적인 과정을 나타냅니다. 여기서 기억을 해주시면 되는 부분은 오직, VAE 모델은 특정 이미지가 입력으로 들어오면, 해당 이미지를 똑같이 출력해내는 과정이구나 정도의 기본적인 느낌만 받아들이시면 됩니다. 저기 보이는 중간 구조들은 등은 일단은 무시해주세요!
여기 예시에서는 4가 들어오고 거의 똑같은 4가 나온거가 보이시죠?

방금과 같은 원리로, 다음 보이는 그림은 VAE 모델을 가지고 MNIST 데이터셋을 생성한 사진입니다. 밑에 latent space의 크기에 따라 미묘하게 다르게 생성된 사진들을 확인할 수 있는데요, 이 latent space 개념은 뒤에가서 설명을 자세히 드리겠습니다.
Background
본격적으로 VAE를 설명 드리기 전에, VAE를 이해하기 위해서 알아둬야할 몇가지 개념들을 설명해드리겠습니다.
Auto-Encoder
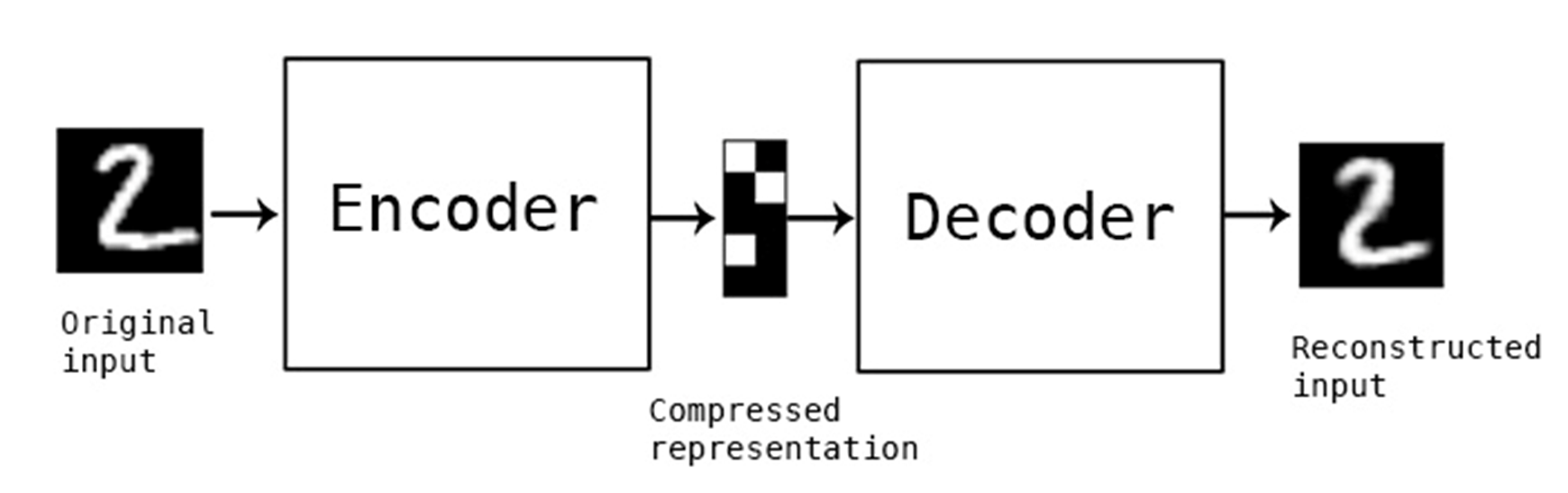
먼저 Auto-Encoder 개념부터 설명을 드리겠습니다.
VAE의 근간이 되는 AutoEncoder역시 Input을 집어 넣어 Input과 동일한 Output을 출력하는 식으로 학습되는 모델입니다.
여기 보이는 예시에서는 2라는 image를 입력을 해주고, encdoer를 통해 encoding을 해주고 -> latent vector를 만들어 준뒤에 latent vector를 Decoder로 넣어 decoding을 거쳐 동일한 2라는 image를 출력을 해줍니다.
하지만 Autoencoder는 VAE와 다르게 기본적으로 Encoder를 구축해서 latent vector를 만들어주기 위해 Decoder를 사용한 개념입니다. 뭐 뒤에 가서도 설명을 드리겠지만, 여기서 간단하게 설명을 드리면 VAE는 Decoder를 구축해서 output을 생성해주기 위해 encoder를 사용했습니다. 따라서, Encoder는 compressed representation이 주된 목적이고, decoder는 generative task가 주된 목적인 점에서 두 모델의 목적이 근본적으로 다르다고 할 수 있습니다.

따라서 방금 구조에서 input을 x라고 보고 output을 y라고 두고 어떻게 학습되는지 알아보겠습니다.
Autoencoder는 원래 기존의 label이 없는 input을 사용하는 비지도학습 기반 문제에서 자기 자신 input을 output과 동일하게 생성해내 게끔 지도학습 기반 문제로 바꾸어서 해결합니다.
먼저 각각의 notation부터 설명 드리면, X,Y는 Input과 output을 의미하고 / h()와 g()는 Encoder와 Decoder를 의미하고 / z는 encode로부터 나온 latent space를 의미합니다.
따라서, latent vector z는 x input이 encode를 통과한 h(x)로 표현이 되고, output y는 z가 input으로 들어가 decoder를 통과한 g(z) 즉, g(h(x))로 표현이 됩니다.
그래서 input X, output Y의 차이인 loss function은 L(x,y)로 표현이 될 수 있고 여기 loss function으로는 MSE를 사용하거나 Cross-Entropy loss를 활용할 수 있습니다.
다만 각 image pixel의 차이를 계산하는 MSE가 더 직관적으로 사용되긴 합니다만, MLE 관점에서 봤을 때, 여기서 사용되는 확률분포가 가우시안 분포를 따르면 MSE를 사용하고 / 베르누이 분포를 따른다고 가정을 하면 CrossEntropy를 사용할 수 있습니다.
그래서 최종적으로 다음 학습을 하면, Autoencoder는 앞서 말씀 드린대로 Encoder가 목적인 모델이었기에, Encoder만 latent vector로 축소하는 차원축소 기법으로 사용을하고/ decoder는 생성하는 성능이 매우 낮기에 따로 사용하지는 않습니다.
Kullback Leibler Divergence
그 다음으로 설명드릴 개념은 KL divergence입니다. 다음 개념에 대한 이해가 없다면, 이따가 뒤에서 다루는 VAE loss function을 이해하기 어렵기 때문에 여기서 간단하게 짚고 넘어가겠습니다.
KL divergence는 단순히 두개의 확률 분포에 대한 차이를 비교하는 개념이라고 이해하시면 됩니다.
만약 우리가 특정 확률 분포 P와 Q의 차이를 알고 싶을 때, KL divergence를 활용할 수 있습니다.
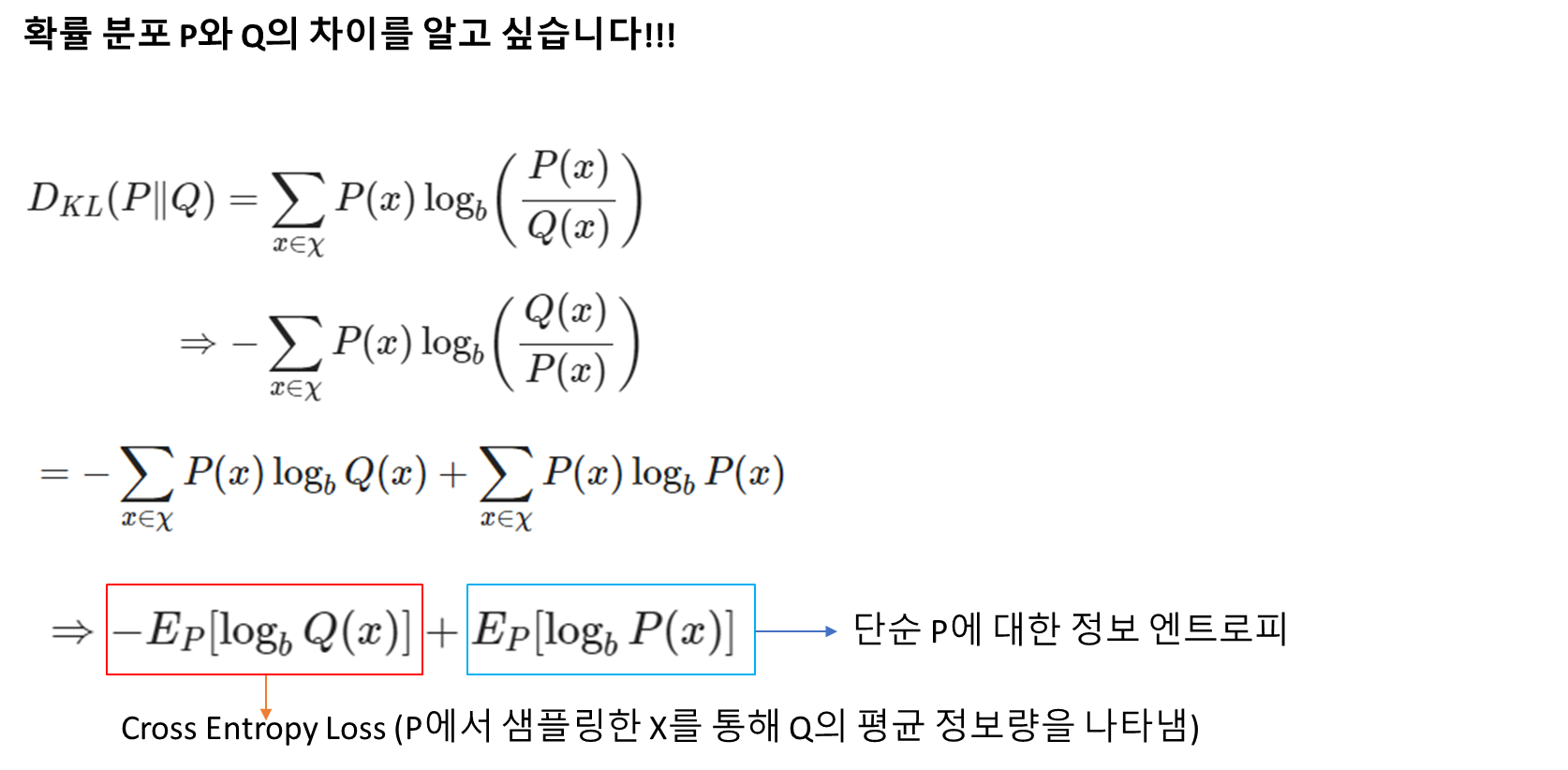
우리가 알고싶은 확률 분포는 P라고 두고 KL divergence를 적용하면, 다음과 같은 식이 나올 수 있습니다. 이 식을 log의 분모 분자 위치를 바꿔 식에 대한 변형을 조금 가해주면, 다음과 같이 두개의 항으로 나타낼 수 있습니다.
그리고 식을 자세히 보시면 두 term에 대해 다 P(x)가 곱해져있기에, 모두 x가 P의 분포를 따를 때의, 기대 값으로 나타내줄 수 있습니다.
최종적으로 보면 KL divergence는 Cross Entropy와 Entropy의 조합으로 이루어져 있다는 것을 볼 쉬 있습니다.
즉 이를 통해서, Q의 분포와 P의 분포가 어느 정도 닮았는지 수치적으로 파악을 할 수 있게 됩니다.
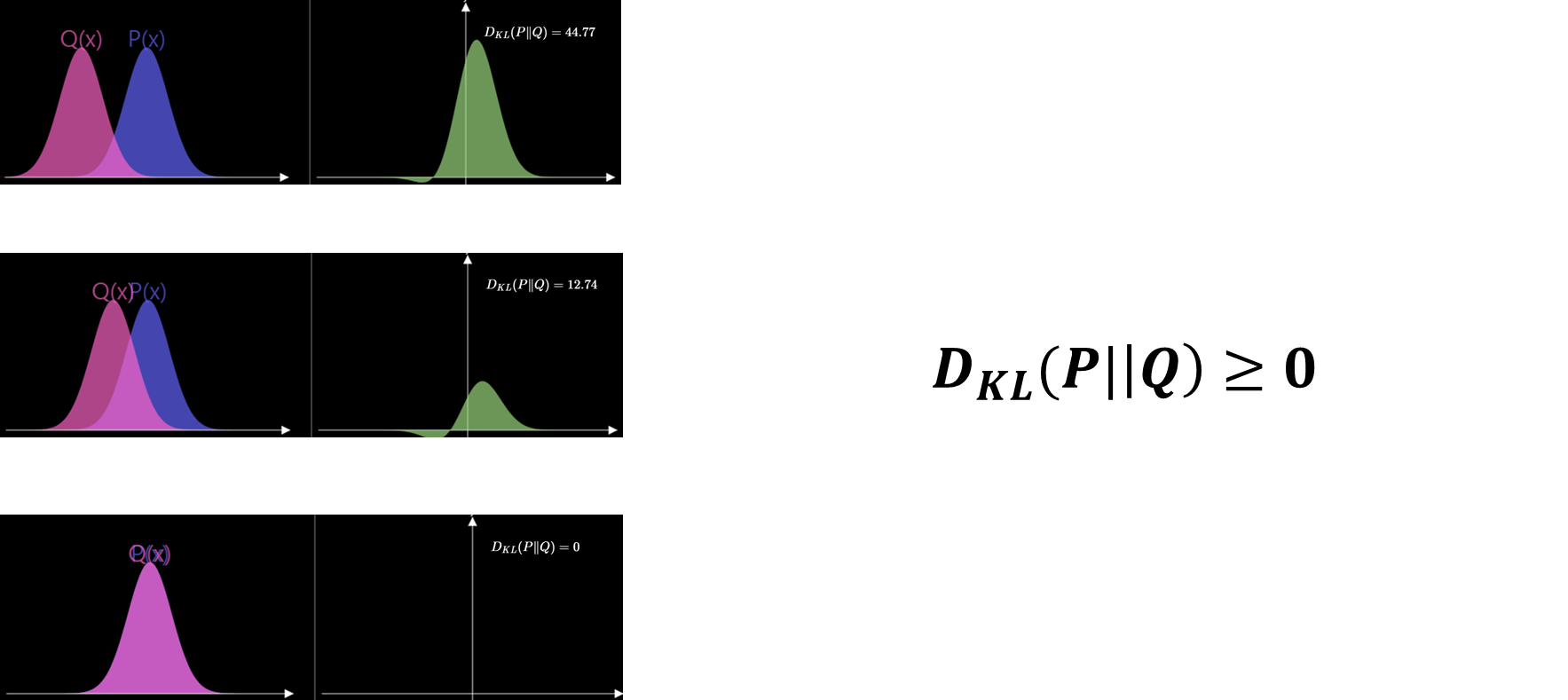
KL divergence의 몇가지 특징을 설명해드리면, 다음 그림을 보면 알 수 있듯이 두 확률 분포간의 차이가 가까워 질수록 KL Divergence 값도 작아지게 됩니다. 두 확률분포가 완전히 동일하게 된다면, KL Divergence 값은 0이 되기 때문에, KL Divergence 값은 모두 0이상인 값을 갖는 것을 알 수 있습니다.
VAE
Architecture
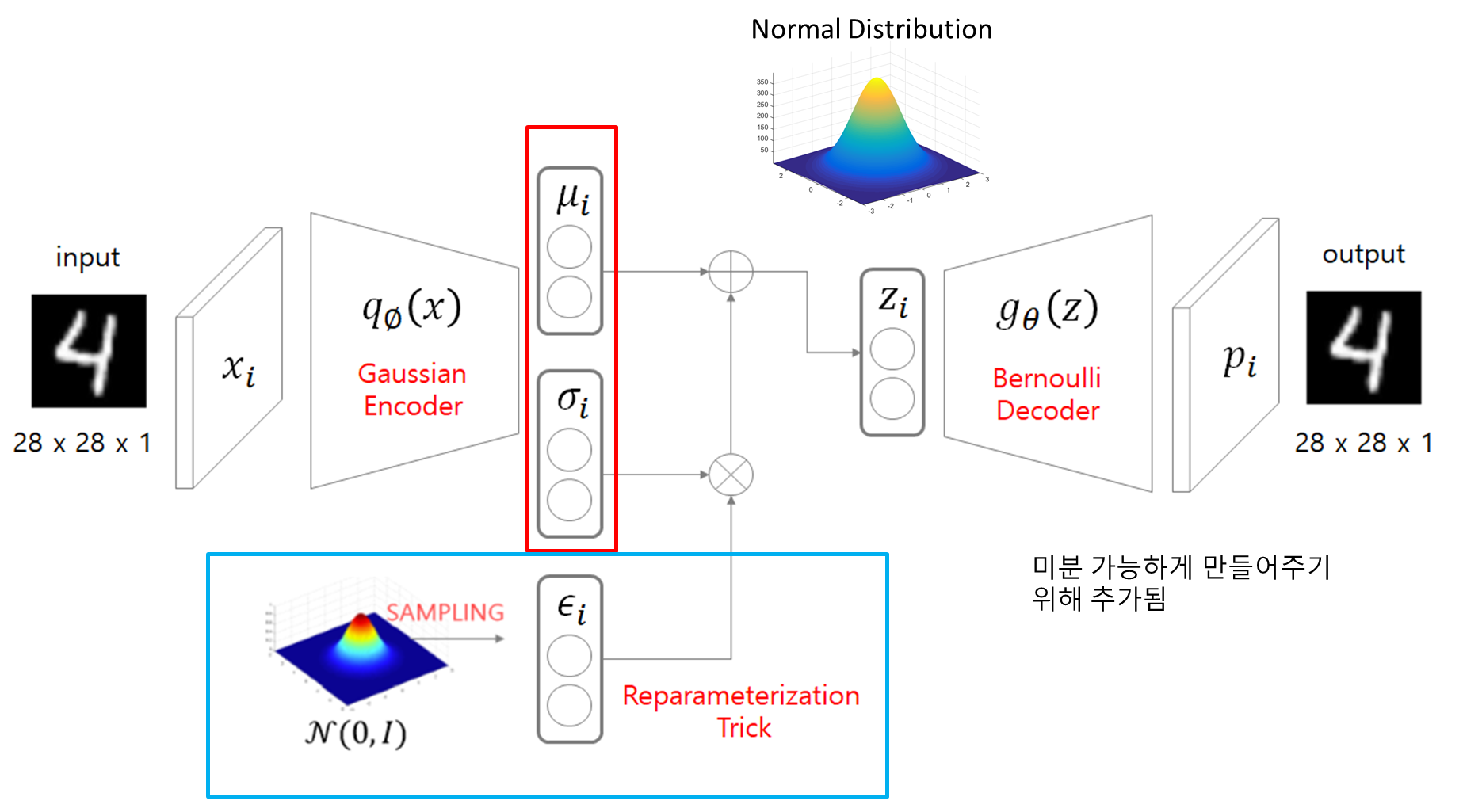
자 이제 기본적인 background 개념들을 알았으니, 본격적으로 VAE의 구조에 대해서 설명을 드리겠습니다.
앞에서 설명드린 바와 같이, VAE는 새로운 데이터를 생성하기 위해서 사용되는 모델이기에 생성하는 Decoder가 주된 목적인 모델입니다.
먼저 Autoencoder는 input image를 Encoder로 들어가게 되면 latent vector z를 출력하는데, 여기 VAE는 Input image가 input으로 들어가게 되면 Encoder를 통해서 평균과 표준편차 (뮤, 시그마)를 출력해냅니다.
따라서 평균과 표준편차를 알 수 있기에, 이 둘을 활용해서 Normal Distribution을 만들어줄 수 있습니다. 그래서 만들어진 정규 분포로부터 샘플링을 통해 z latent variable을 만들어내고, z를 다시 Decoder로 통과시켜 input과 동일한 output값을 출력해줄 수 있습니다.
그리고 저렇게 평균과 표준표차를 통해 만들어진 정규분포에서 샘플링하는 것은 학습과정에서 역전파를 실행할 때, 불가능합니다.
그래서 여기 파란색 박스로 박스쳐진, Reparameterization trick을 도입해 역전파를 가능하게 만들어줍니다.
전체적인 개요는 다음과 같고 이제 하나하나 수식적으로 해당 과정을 구체적으로 설명드리겠습니다.

다음은 VAE의 loss function에 대해서 알려드리겠습니다
VAE Loss function 에러는 크게 두가지가 있는데, 하나는 Reconstruction Error가 있고 다른 하나는 Regularization이 있습니다.
Reconstruction Error는 방금 설명드렸던 AutoEncoder와 동일하게 원본 입력값을 출력으로 생성할 수 있게 복원해주는 loss function 입니다.
확률을 Normal Distribution으로 가정하면 MSE가 되고, 베르누이 분포로 가정하면 Cross Entropy가 되는데, 다음 Reconstruction error의 확률은 베르누이 분포를 가정했기에 cross entropy와 같이 됩니다.
두번째 에러는, VAE는 정규분포에서 샘플링한 z를 뽑기에, z가 정규분포를 따른다는 가정을 앞선 장표에서 설명 드렸는데, 그러한 가정을 충족시켜주기 위해 Regularization loss term을 넣어주어 optimizing할 때, 정규분포로 근사하게 만들어 줍니다.
따라서, 파란색으로 적힌 식을 확인해보면, p(z)는 정규분포라고 가정을 했을 때, i번째 input x가 인코더를 통과하는 z값에 대한 확률분포가 p(z)의 확률분포인 정규분포와 비슷해지게 만들어줍니다.
Loss Function

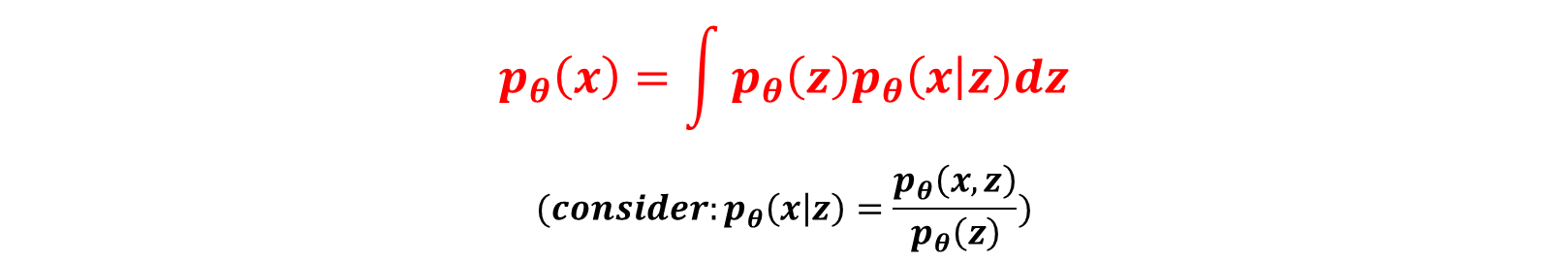
VAE는 AE와 마찬가지로 z latent variable에서 x를 생성합니다.
저희가 알고 싶은 것은 일단 x에 확률 분포이기 때문에, x의 likelihood를 최대화하는 식으로 MLE를 진행하면 되겟다는 생각을 할 수 있습니다.
그래서 밑에 식을 보시면 베이지안 rule에 따라서 p(x)를 다음과 같이 적분 형태로 표현해줄 수 잇습니다.
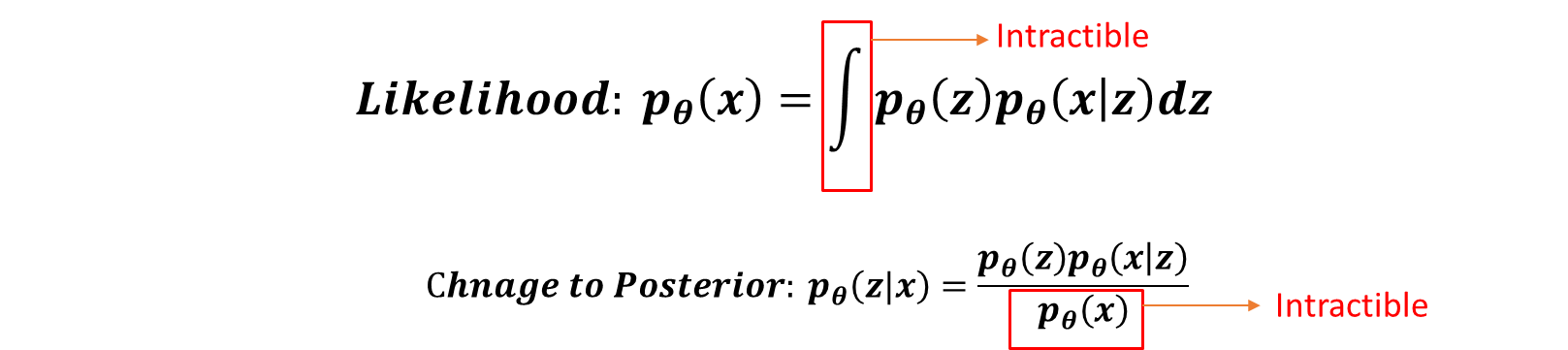

자 다시 likelihood 식을 보시면, 적분 안에 있는 첫번째 term인 p(z)는 저희가 gaussian distribution을 따른다고 가정을 해서 아는 값이고, p(x|z)도 latent space z가 들어올 때, x를 출력하는 구조인 Decoder를 생각하면 되니 아는 값이지만 모든 z에 대해서 적분을 할 수 없다는 문제가 있기 때문에, 이 값을 구할 수가 없습니다.
그래서 다음 likelihood를 posterior 사후 확률로 바꿔서 문제를 바라봐도 , 분모의 p(x)부분이 애초에 위에 몰라서 구하려고 했던 likelihood 값이기 때문에 구할 수가 없다는 것을 알 수 있습니다.
따라서, Decoder만 가지고 학습을 하는 것은 불가능하다고 판단이 되니 Encoder를 사용해서 이런 계산이 안되는 부분을 해결하려는 시도가 있었습니다. 즉, z given x의 인코더 확률분포와 z given x의 디코더 확률분포와의 근사를 시키도록 만들어줬습니다.

여기 위에 보이는 장표는, loss function을 풀어쓴 수식입니다. 해당 수식 과정을 통해 reconstruction error와 regularization이 어떻게 도출되었는지 설명 드리겠습니다. 위에서 data likelihood인 p(x)를 maximize하겠다고 말씀을 드렸습니다. 해당 log(p(x))는 단조 증가함수 log를 씌워주고 Expectation 형식으로 바꿔줄 수 있습니다. 다만 조건으로 z의 분포가 x가 인코더를 거쳐서 나오는 확률 분포를 걸어줘야 합니다. 그러면 Bayes 규칙으로 인해 log 안에 값을 변형시켜 줄 수 있고, 다음에 분모 분자에 같은 q_pi 값을 곱해줄 수 있습니다. 따라서, 해당 expectation 식을 3개의 항으로 분리해 줄 수 있는데(분모, 분자 항을 cross over형태로 묶어주어 정리), 두번째 항과 세번째 항은 앞에서 간단하게 설명드린 KL divergence의 꼴로 변형시켜줄 수 있습니다. 다만 세번째 항은 decoder에서의 x given z 확률을 구해야 값을 구할 수 있는데, 이는 본래 decoder가 z given x의 상황을 생각해보면 구할수 없는 값이라는 것을 알 수 있습니다. 다만 세번째 항도 KL divergence로 부터 나오는 값이니깐 저희는 0이상인 값이라는 것을 알 수 있습니다.

즉, 결론적으로 저희는 해당 식을 maximize하는 것을 고려하고 있었기에, 앞에 두개의 항을 lower bound("ELBO")로 생각할 수 있고, 세번째 항은 무시해줄 수 있습니다.

방금까지 설명을 드린 부분의 term에 각각 의미를 부여해주면 reconstruction error 와 regularization 부분 으로 나누어 볼 수 있습니다.
MLE 문제를 따라서, NLL form으로 바꿔 부호를 바꿔주면 다음과 같은 식으로 바뀌게 되어서 다음 세타와 파이 파라미터를 찾는 최적화 문제로 바뀌게 됩니다.
Regularization
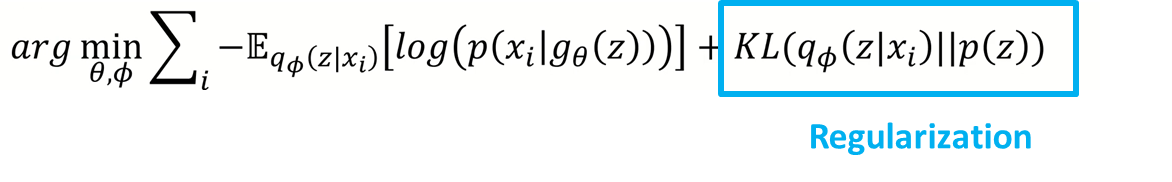

Regularization loss term부터 먼저 보시면, 두가지 가정이 들어가는데, 첫번째 가정은 Encoder를 통과해서 나오는 분포는 다변량 정규분포를 따르는 것입니다.
그리고 두번째 가정은 latent space z의 분포는 표준정규분포를 따른다고 간단하게 가정을 했습니다.
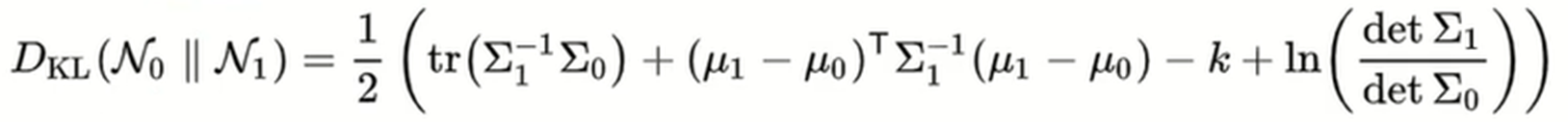
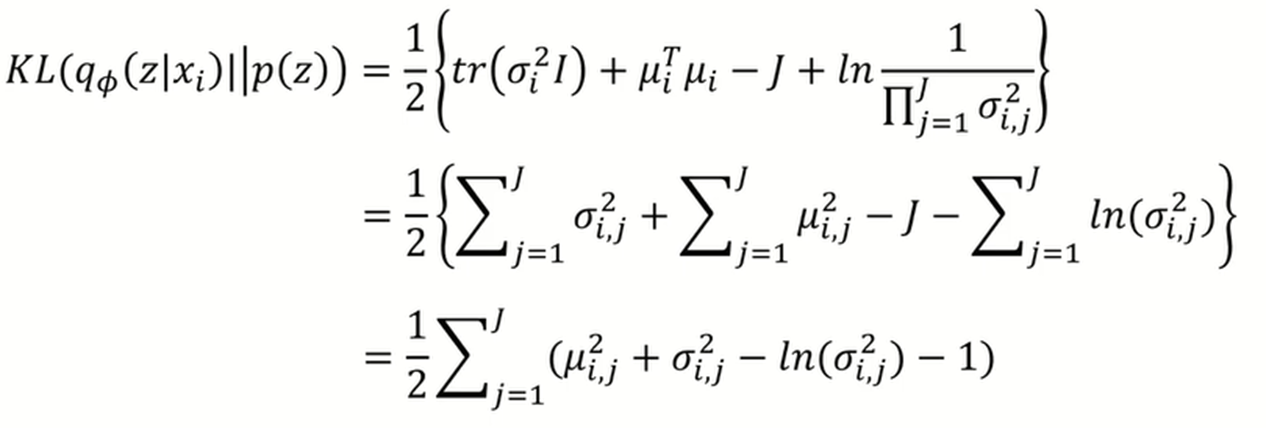
먼저 다변량 정규분포에서의 KL divergence는 다음과 같은 식으로 표현이 되는데, P(z)는 앞에서 표준 정규 분포를 따른다고 가정을 했으니, 이 N1 부분의 식에가다가 평균이 0이고 표준편차가 1인 값들을 대입해주면 식은 다음과 같이 정리가 됩니다.
Reconstruction Error


이번에는 Reconstruction Loss를 확인해보겠습니다.
Expectation이기 때문에, 따르는 분포 값과 안에 값을 곱해주어서 다음과 같이 나타내주고 모든 z에 대해서 적분하는 것으로 나타내줄 수 있습니다.
그런데 앞에서 설명드렸다시피 모든 z에대해서 적분하는 것은 어렵기때문에 여기서 또 다시 sampling 기법을 적용해주어서 해결합니다.
몬테 카를로 시뮬레이션 방법을 적용해서 z를 적당히 큰 수 만큼 샘플링해서 평균내는 식으로 대표값을 정해줄 수 있는데, 이것은 학습시에 연산량에 있어 bottleneck이 될 수 있어 연산량을 올리기 위해 되게 naïve한 가정으로 한 번만 추출을 해서 그 z값을 대표값으로 사용했습니다.
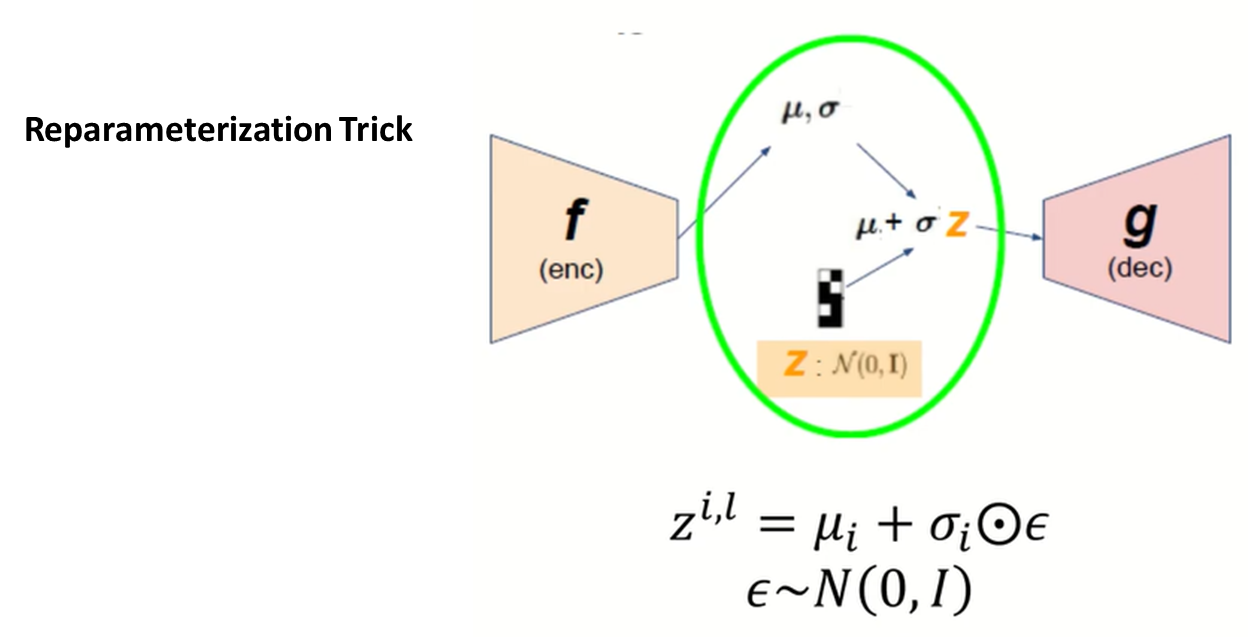
다음은 Reconstruction error에서 사용된 reparameterization trick에 대해서 설명해드리겠습니다.
Encoder에서 나온 평균과 시그마로 바로 정규분포를 구축하고 이에 대해서 샘플링을 하면 미분을 할 수 없는 문제가 있었다고 앞에서 설명드렸습니다.
그래서 이렇게 표준정규분포를 따르는 엡실론에 대해서 Encoder에서 나온 표준편차에 곱해주고 이를 다시 평균과 더해주는 연산을 취해준다면 미분을 할 수 있게 됩니다.


따라서 저기 reconstruction error를 다시 정리해서 말씀 드리면, 저 값을 적분해서 구해야하는데, 그렇게 못하니 샘플링 기법을 통해 근사화를 시켜야하는데, 그것조차도 연산시에 문제가 생겨서 한 번만 샘플링해서 나온 저 녹색값을 구하는 거라고 아시면 될 것 같습니다.
그래서 log x given z를 전체 데이터셋에 대해서 취해주면, 디코더에서 사용되는 p의 확률분포가 베르누이 분포를 따른다고 가정을 했을 때, 단순히 확률의 곱으로 표현을 해줄 수 있고 로그의 성질에 따라 전체 값을 log의 summation으로 나타내줄 수 있습니다.
그리고, 베르누이 식으로 바꿔주게 되고 log의 정리를 하면 최종적으로 cross entropy식으로 나타내 줄 수 있습니다.
여기 p의 확률분포를 베르누이가 아닌 가우시안 분포로 가정을 했을 때, 결국에는 mean squared error로 표현이 되는데, 위 설명이 궁금하신 분은 따로 연락주시면 감사하겠습니다.
Summary
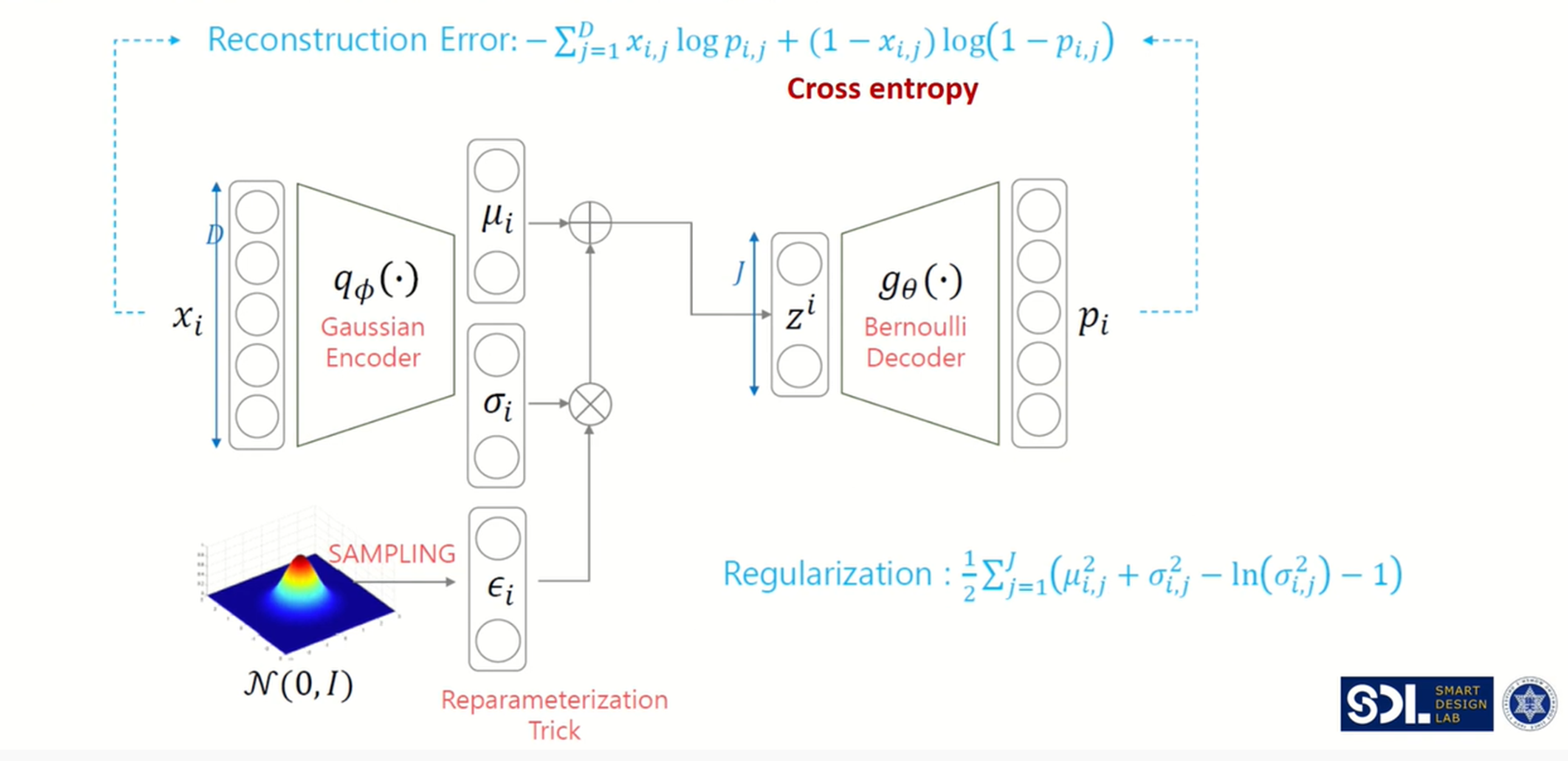
다시 한 번 전체 VAE에 대해서 복습을 하고 마무리를 하겠습니다.
X input data가 Gaussian Encoder로 들어가면 평균과 표준편차를 출력으로 나타내주고, (여기서 평균과 표준편차가 정규분포를 따른다고 가정했으니 Encoder는 Gaussian Encoder라고 부른다고 합니다), 해당 평균과 표준편차를 갖는 정규분포를 통해 z값을 sampling 해주는데, 바로 sampling을 적용하면 미분을 할 수 없어 역전파가 안된다는 문제가 생겨 아래와 같이 reparameterization trick을 적용해줍니다. 그리고 latent vector z를 베르누이를 따르는 디코더를 통과하게 되면 다음과 같은 두 개의 loss function인 reconstruction error와 regularization error를 갖게 됩니다.

VAE의 특징은 다음과 같습니다. Decoder는 최소한 학습 데이터를 생성해 낼 수 있고, Encoder는 최소한 학습 데이터를 latent vector로 잘 represent할 수 있다는 성질이 있습니다. 그래서 VAE의 목적이 사실 생성이었던 Decoder였지만, 결과론적으로 latent vector를 더 잘 만들어서 주로 Encoder를 활용하기 위해 사용이 많이 됩니다.

안녕하세요 좋은 글 감사합니다. 오타가 있는거 같아서 댓글 남깁니다!
"다만 세번째 항은 decoder에서의 x given z 확률을 구해야 값을 구할 수 있는데" 부분에서
z given x 로 정정해야할 거 같습니다.