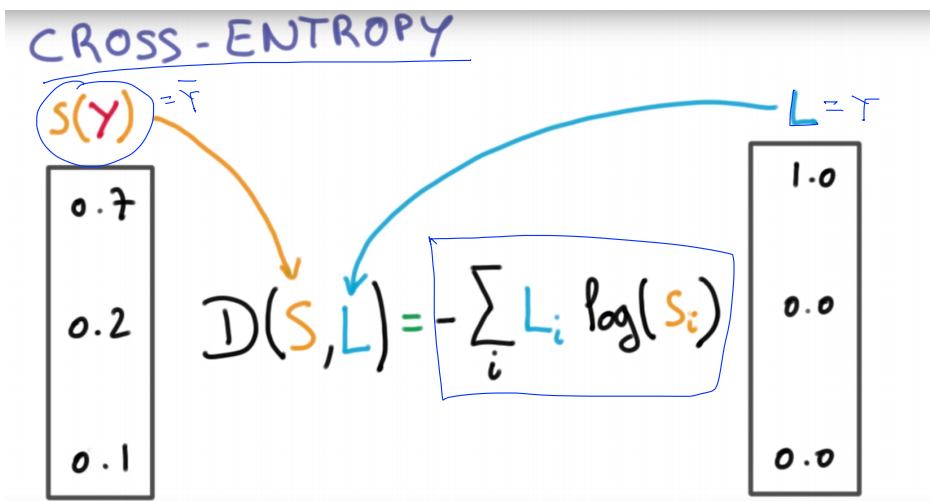
앞에서 살펴봐왔던 Classification 이라는 지도학습을 통해, 모델이 예측한 클래스가 라벨링 되었다면, 이를 기반으로 모델이 잘 예측했는 지에 대해 Cost Function (Loss 함수)을 정의해 평가를 해준다.
Cost function = (sotmax가 예측한 값)과 (실제 Y의 값)의 차이를 계산 = Distance(S, L)
예측이 맞을 경우 작은 값이 되고, 틀릴 경우 큰 값이 된다.

그 중에 하나인, 'Cross Entropy' 라는 것을 살펴보기 전에, '정보이론'을 먼저 살펴본다.
정보이론(Information Theory)
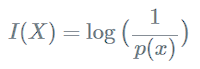
- 정보(information)란 불확실성의, 미지의 정도를 수치화
- 확률 함수를 이용해 정의
- 정보량은 확률에 반비례
- 어떤 사람이 정보를 더 많이 알수록 새롭게 알 수 있는 정보는 적어짐
자주 발생하는 사건 (정보량이 비교적 낮다)
희박한 확률로 발생하는 사건 (정보량이 비교적 많다)
예시 ) 미국 복권 (메가밀리언) vs 한국 복권 (로또)
메가밀리언 당첨 확률 : 1/3억 260만
로또 당첨 확률 : 1/814만 5,060
→ 메가밀리언이 로또보다 정보량이 많다.
Entropy
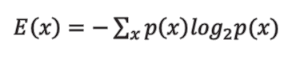
확률적으로 발생하는 사건에 대한 정보량의 평균을 의미.
어떤 데이터가 나올지 예측하기 어려운 경우라는 의미의 '불확실성'과 실제 데이터 간의 차이.
즉, '내가 갖고 있는 정보와 실제로 일어난 정보 간의 격차'처럼 말이다.
Entropy는 정보량에 대한 기댓값이며, 동시에 사건을 표현하기 위해 요구되는 평균 자원이라고도 할 수 있다.
Cross Entropy
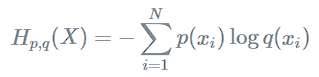
두 개의 확률분포 와 에 대해 하나의 사건 가 갖는 정보량으로 정의.
즉, 서로 다른 두 확률분포에 대해 같은 사건이 가지는 정보량을 계산한 것.
실제 분포 에 대하여 알지 못하는 상태에서, 모델링을 통하여 구한 분포인 를 통하여 를 예측하는 것.
와 가 모두 들어가서 Cross Entropy라고 함.
- 머신러닝을 하는 경우에 실제 환경의 값과 를, 예측값(관찰값) 를 모두 알고 있는 경우,
- "머신러닝의 모델은 몇 %의 확률로 예측했는데, 실제 확률은 몇 %야 !" 라는 사실을 알고 있을 때 사용.
Cross Entropy에서는 실제값과 예측값이 맞는 경우에는 0으로 수렴하고, 값이 틀릴 경우에는 값이 커지기 때문에, 실제 값과 예측 값의 차이를 줄이기 위한 Entropy라고 보면 될 것 같다.
- 모델을 잘 학습한다는 것은 정답의 분포를 모델이 잘 따라 하도록 하는 것.
→ 즉, 정답 분포와 모델이 예측한 값의 분포가 비슷해지도록 하면 좋은 것.