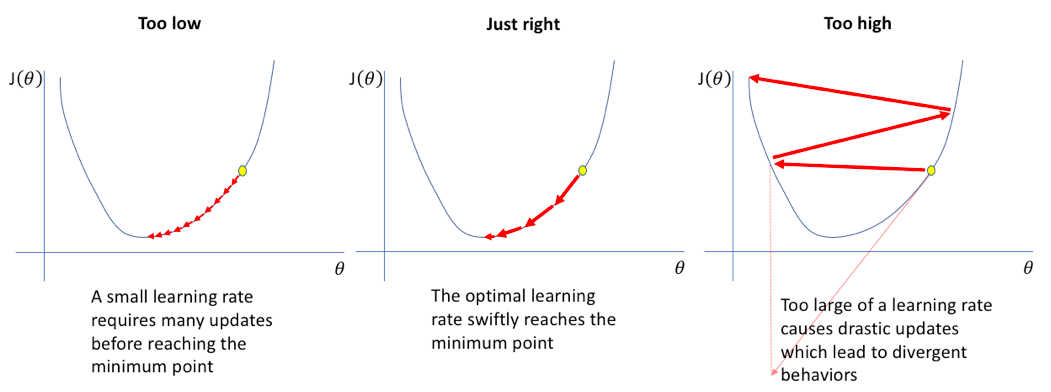
Gradient Descent
-
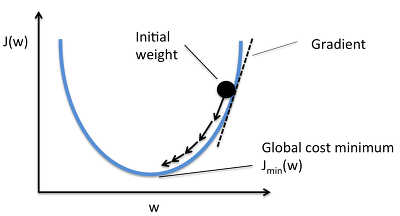
현재 네트워크의 weight에서 내가 가진 데이터를 다 넣어주면 전체 에러(Cost Function)가 계산된다.
-
미분을 하면 에러를 줄이는 방향을 알 수 있다.
-
그 방향으로 정해진 스텝량(learning rate)을 곱해서 weight을 이동시킨다.
-
계속 반복해서 학습.

Gradient Descent의 경우 항상 전체 데이터 셋을 가지고 한 발자국 씩 전진 (step = learning)할 때마다, 최적의 값을 찾아 나아가고 있는 모습을 볼 수 있다.
Learning Rate (Step Size)
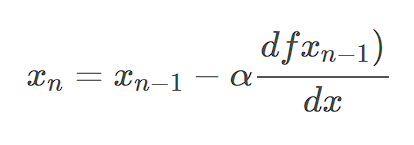
경사하강법 알고리즘은 기울기에 학습률(Learning rate) 또는 보폭(Step size)이라 불리는 스칼라를 곱해 다음 지점을 결정
Local minimum에 효율적으로 도달할 수 있도록, 너무 크지도 작지도 않은 적절한 학습률을 세팅해야 함.
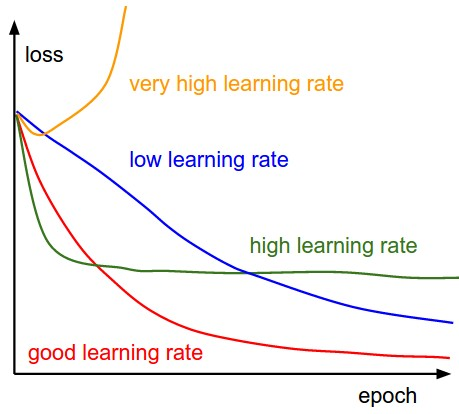
- loss : cost function
- epoch : number of iterations
-
low learning rate: 손실(loss) 감소가 선형의 형태를 보이면서 천천히 학습됨.
-
high learning rate: 손실 감소가 지수적인(exponential) 형태를 보이며, 구간에 따라 빠른 학습 혹은 정체가 보임.
-
very high learning rate: 매우 높은 학습률은 경우에 따라, 손실을 오히려 증가시키는 상황을 발생.
-
good learning rate: 적절한 학습 곡선의 형태로, Learning rate를 조절하면서 찾아내야 함.
한 걸음 나아가기 위한 보폭이 낮으면 학습하는데 오래 걸리고, 너무 크면 최적의 값을 찾지 못하는 문제가 있다.
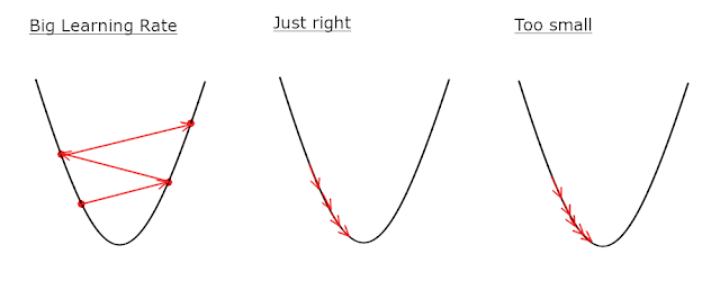
학습률이 큰 경우 : 데이터가 무질서하게 이탈하며, 최저점에 수렴하지 못 함.
학습률이 작은 경우 : 학습시간이 매우 오래 걸리며, 최저점에 도달하지 못 함.
미분값과 Gradient Descent와의 관계
이론상으로는 미분값(미분계수)가 0인 지점을 찾는 방식(단순 mse 체크)도 분명히 유효하다.
그러나 미분값으로만 gradient descent를 진행하지 않는 이유는 아래와 같다.
-
우리가 주로 실제 분석에서 맞딱드리게 되는 함수들은 닫힌 형태(closed form)가 아닌 경우가 많음.
-
함수의 형태가 복잡해 (가령, 비선형함수) 미분계수와 그 근을 계산하기 어려운 경우가 많음.
-
실제 미분계수를 계산하는 과정을 gradient descent는 컴퓨터로 비교적 쉽게 구현할 수 있다.
※ 일차미분을 그대로 step size로 하는 것은 너무 이동량이 크기 때문에 실제 문제에서는 일차미분에 (1보다 작은) 가중치 상수를 곱해서 빼준다.
ref)
https://seamless.tistory.com/38
https://bioinformaticsandme.tistory.com/130
https://angeloyeo.github.io/2020/08/16/gradient_descent.html
https://darkpgmr.tistory.com/133