#27 Gradient Descent (경사 하강법)

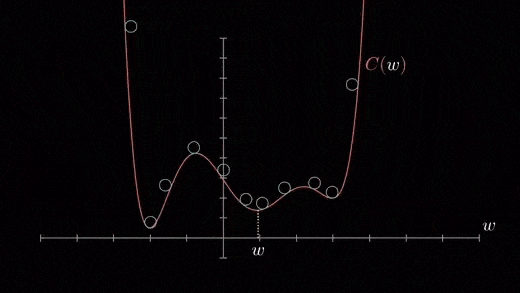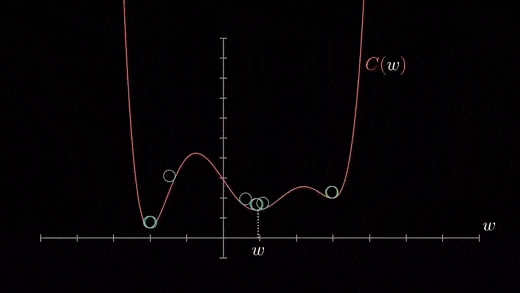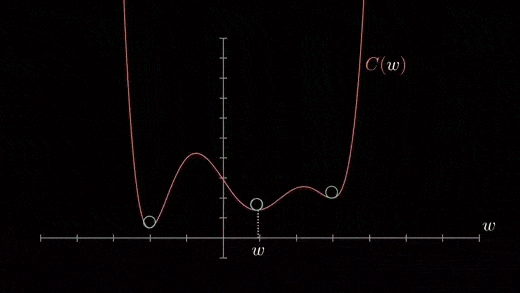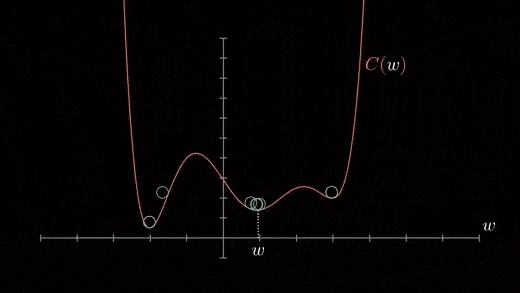
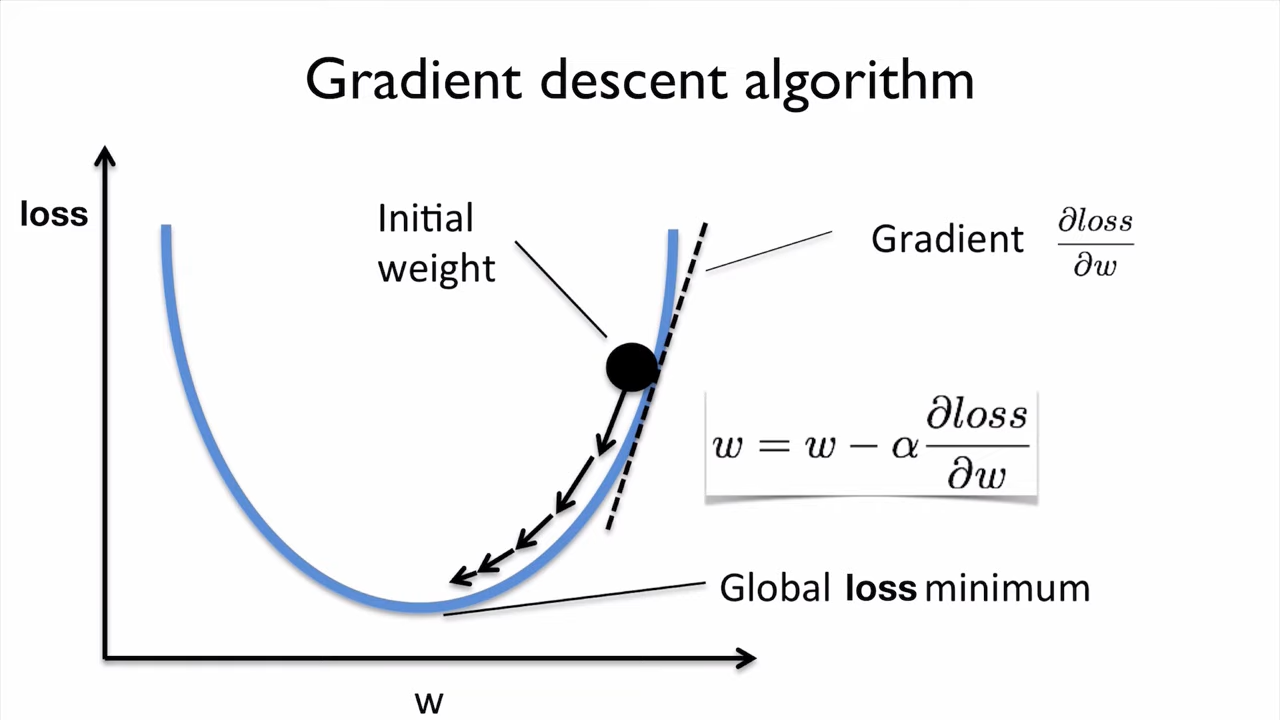
경사 하강법

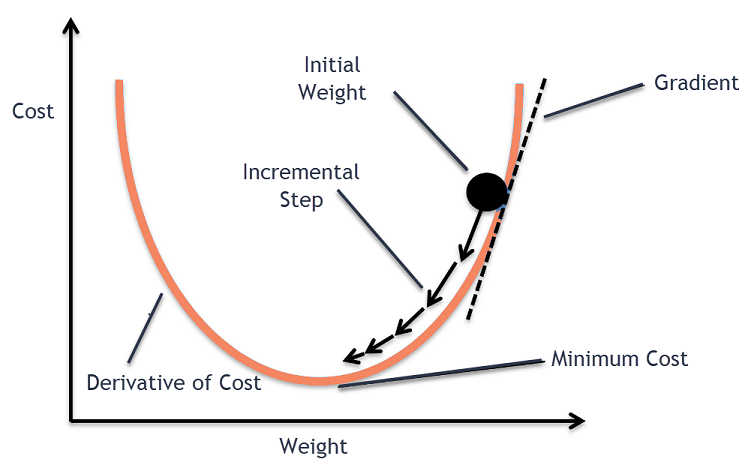
함수 값이 낮아지는 방향으로 이동하며 최솟값을 탐색하는 방식

→ 아무 것도 보이지 않는 산에서 낮아지는 방향으로 이동하여 한 발자국 씩 산을 내려가는 방법.

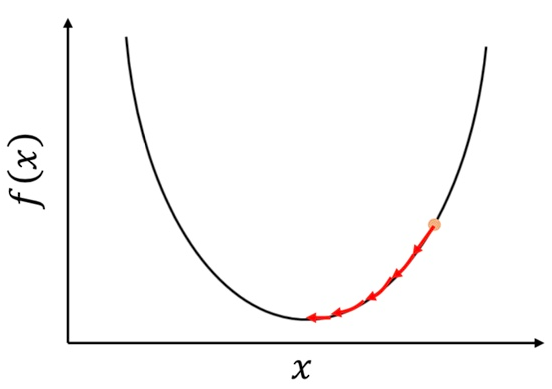
기울기가 양수: x가 커질수록 값이 커짐
기울기가 음수: x가 커질수록 값이 작아짐

기울기 부호의 반대로 움직여야 최솟값으로 가는 방향

경사 하강 알고리즘은 비용 함수 $J(θ(0),θ(1))$를 최소화 하는 $θ$를 구하는 알고리즘이다.

$θ$ 는 parameter들을 의미하는데, $θ_0$ 는 bias (편향) 를, $θ_1$ 는 Weight (가중치, 가설 함수에서의 기울기) 를 의미한다.

$α$는 최적화 프로세스의 조정 매개변수(Hyper-Parameter)인 학습률(Learning Rate)이라고 한다. 단계의 길이를 결정한다.

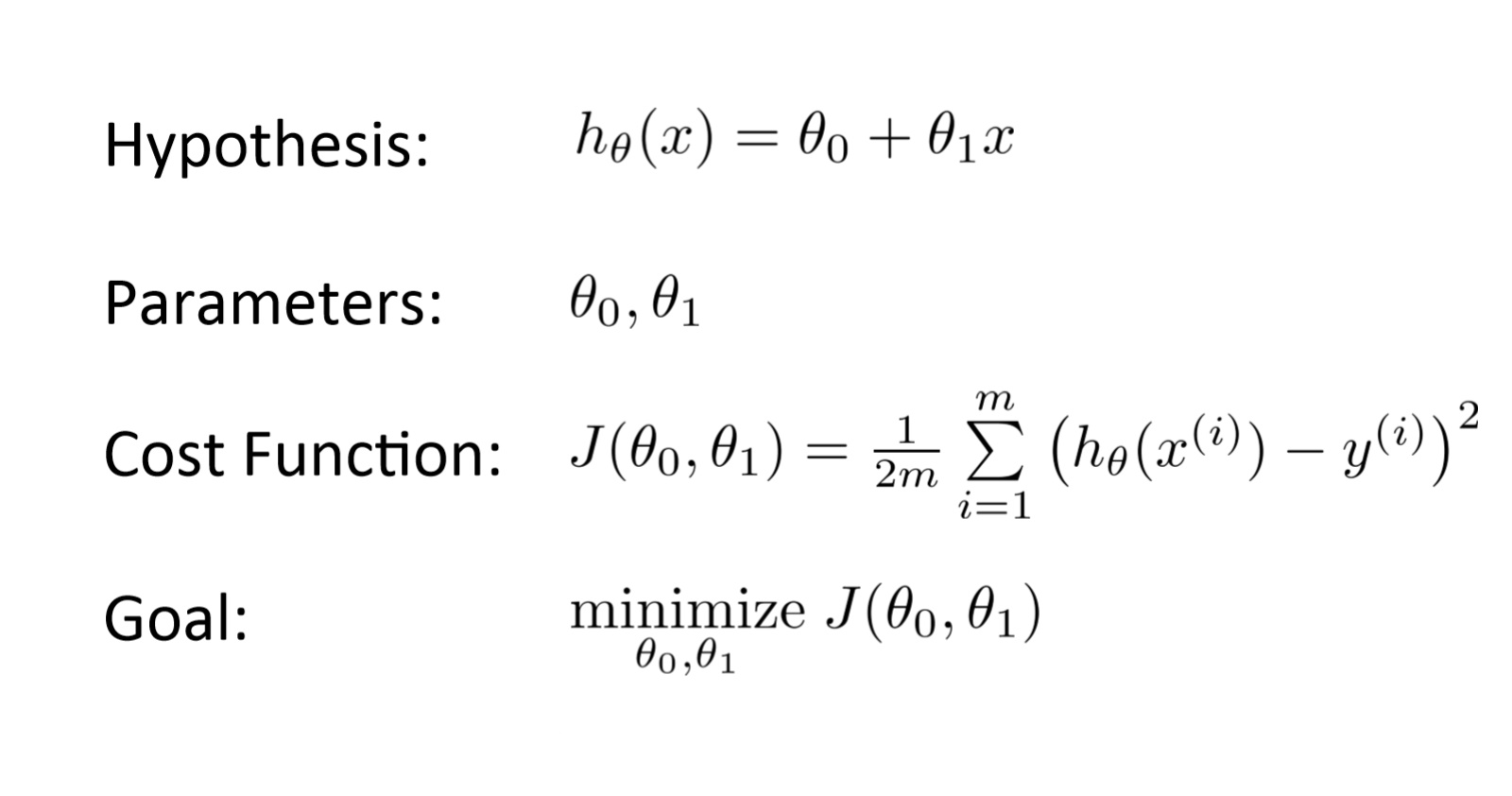
작동 방식

경사하강법 알고리즘의 목표는 주어진 함수 (예: 비용 함수) 를 최소화하는 것이다. 이 목표를 달성하기 위해 두 단계를 반복적으로 수행한다.

1. 해당 지점에서 함수의 1차 도함수인 기울기(Weight)를 계산한다.

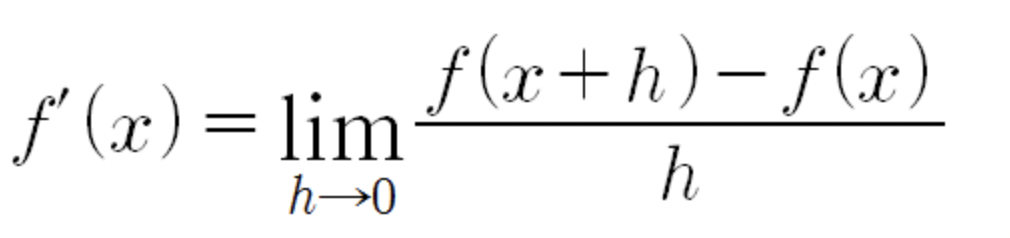
2. 기울기의 반대 방향 으로 스텝(이동)을 하고 기울기의 반대 방향은 현재 점에서 그 점에서의 기울기를 $α$배만큼 증가시킨다.

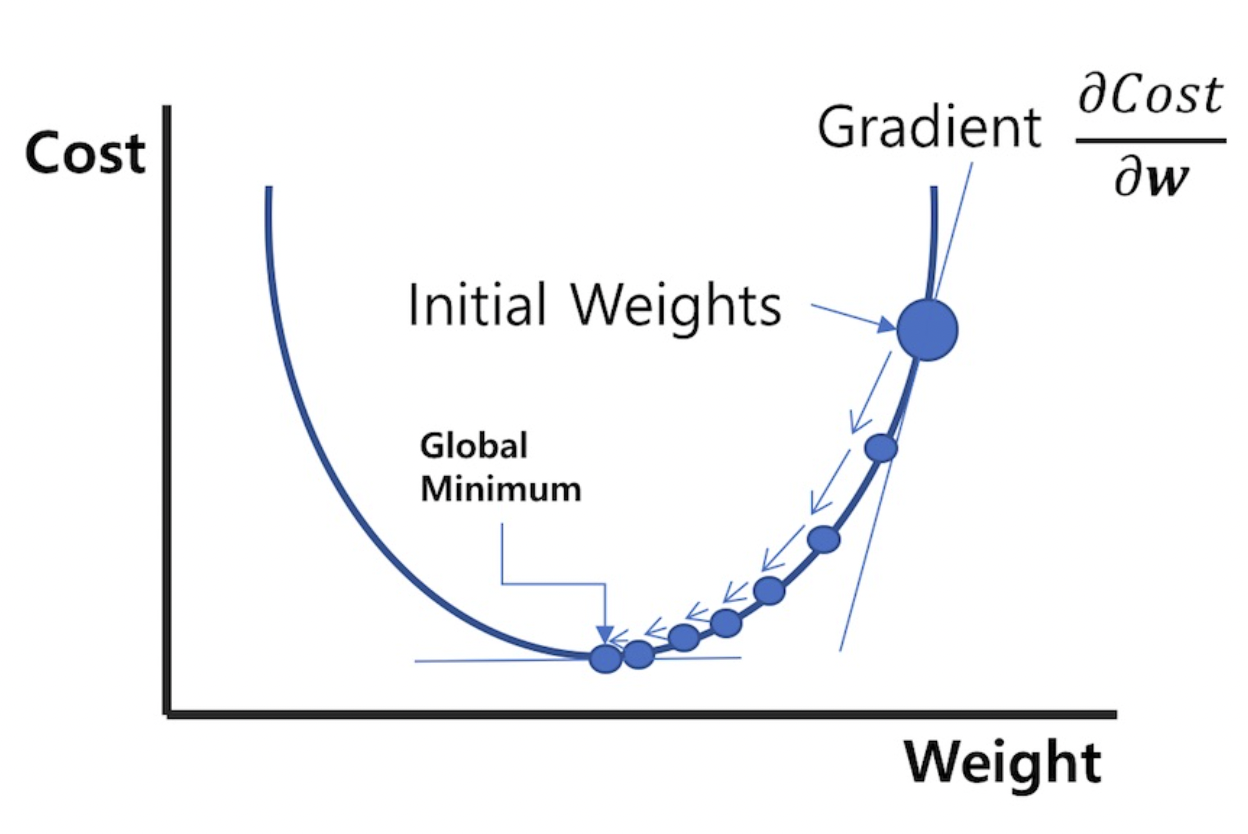
좀 더 풀어서 설명하자면,

1. $θ$에 대해 임의의 초기값 즉, 시작점을 잡는다.

2. 그리고 $J$가 최소가 될때까지 $θ$값 갱신을 반복하여 최솟값에 도달했을 때 해당하는 $θ$를 찾아낸다.

ref) https://www.analyticsvidhya.com/blog/2020/10/how-does-the-gradient-descent-algorithm-work-in-machine-learning/