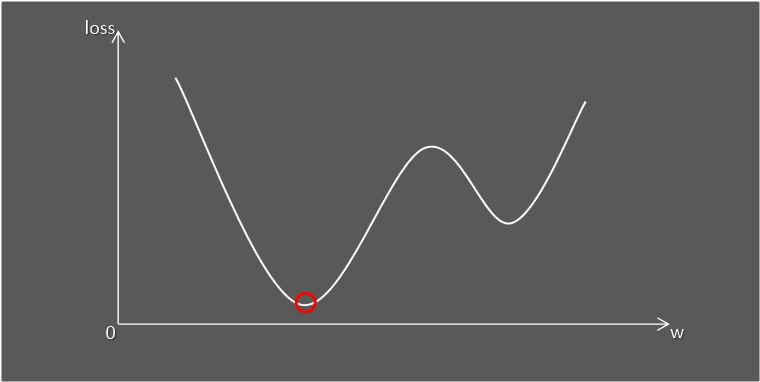
현대 인공지능의 큰 축을 만든 개념 경사하강법(Gradient Descent)에 대해 공부하려고 합니다.
저도 다시 공부할 겸 매우 중요한 개념이니 이렇게 글로 작성해봅니다.
피드백은 언제나 환영입니다.😉
경사하강법(Gradient Descent)
앞서 위에서도 설명했지만 경사하강법은 딥러닝의 시대를 열었다고 해도 과언이 아닙니다.
경사하강법을 이용하면서 "기계가 스스로 학습한다"라는 개념이 더 명확해졌기 때문입니다.
이름에서도 알 수 있듯이 미분을 통해 손실함수의 Global Minima부분으로 갈 수 있도록 하는 방법입니다.
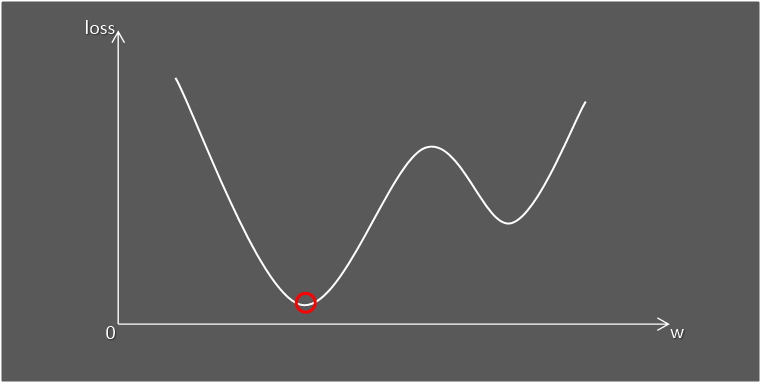
예를들어, 산 꼭대기에 갇혀있는 상황을 생각해봅시다.
날은 어두워서 앞이 아예 보이지 않습니다.
이런 상황에서 어떻게 하면 가장 아래로 내려갈 수 있을까요?
이때 이 '어떻게'가 경사하강법입니다.
우리는 모델이 예측하고 그에 따른 에러값을 보게 됩니다. 이렇게 파라미터에 따라 나타나는 에러값의 집합을 손실함수(Loss Function)라고 부릅니다.
우리는 이런 손실함수를 최소화하는 것을 목표로 합니다.
어떤 회귀문제를 풀어야 한다고 할 때
손실함수 MSE(Mean Squared Error)를 최소화해야 한다면 MSE의 공식은 다음처럼 표현할 수 있습니다.
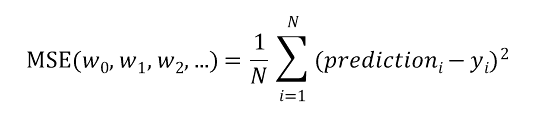
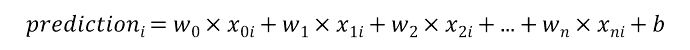
앞서 저희는 손실함수가 최소가되는 Global Minima를 찾아야 한다고 했습니다.
즉, MSE를 최소화하는 w값을 찾는 것이 목표라고 할 수 있습니다.
하지만, 위처럼 식이 복잡해지는 경우 최솟값을 찾기 힘들어집니다.
이때, 경사하강법은 손실함수를 각 변수에 따라 편미분을 적용시켜 Global Minima를 찾습니다.
쉽게 설명하기 위해 w변수는 2개가 존재한다고 가정하겠습니다.
이때 MSE를 풀어서 표현하면 다음과 같습니다.
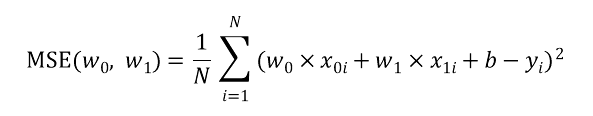
이제 MSE함수를 w0와 w1에 대해 각각 편미분 시켜보겠습니다.
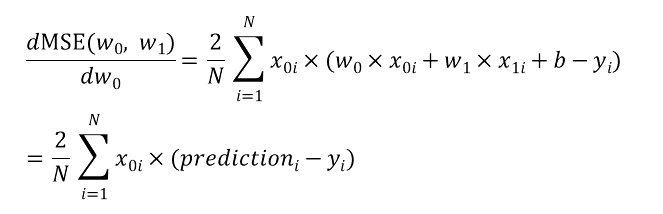
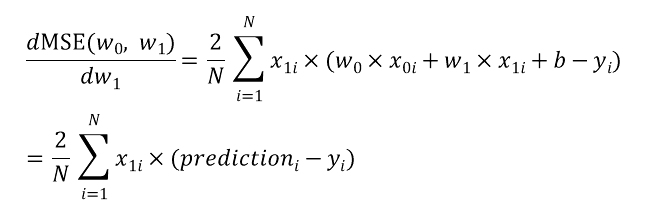
이렇게 각 변수에 대해 편미분한 미분값을 각 변수(w)에 learning rate와 기존 값을 통해 업데이트 되는 값을 보면 다음과 같습니다.
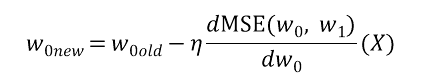
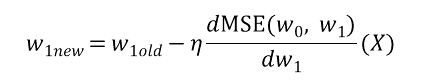
이렇게 계속해서 '특정 변수에 대해 편미분을 적용시켜가며 변수를 업데이트 하는 것'이 경사하강법입니다.
직접 선형함수를 만들어 경사하강법을 이용해 해결하는 로직을 만들어보면 다음과 같습니다.
최종적으로 w0=2, w1=-30에 근접해야 하는 true_function을 만들어줍니다.
import numpy as np
def true_function(X):
return 2*X[:,0] - 30*X[:,1]
def Gradient_Descent(X, Y, w0, w1, learning_rate=0.001):
N = X.shape[0]
prediction = w0*X[:, 0] + w1*X[:, 1]
diff = prediction - Y
w0_update = w0 - learning_rate*(2/N)*(np.dot(X[:, 0].T, diff))
w1_update = w1 - learning_rate*(2/N)*(np.dot(X[:, 1].T, diff))
return w0_update, w1_update, diff
def iteration(X, Y, iter=1000, learning_rate=0.001):
w0 = 1
w1 = 1
global_minima_mse = 10**9
final_w0, final_w1 = 0, 0
for i in range(iter):
w0, w1, diff = Gradient_Descent(X, Y, w0, w1, learning_rate=learning_rate)
N = X.shape[0]
mse = np.mean(np.square(diff))
print('[{0}/{1}] w0:{2}, w1:{3}, MSE: {4:.3f}'.format(i+1, iter, w0, w1, mse))
if mse < global_minima_mse:
global_minima_mse = mse
final_w0 = w0
final_w1 = w1
return global_minima_mse, final_w0, final_w1
np.random.seed(0)
X = 12*np.random.randn(100,2)
Y = true_function(X)
global_minima_mse, final_w0, final_w1 = iteration(X, Y, iter=500, learning_rate=0.00002)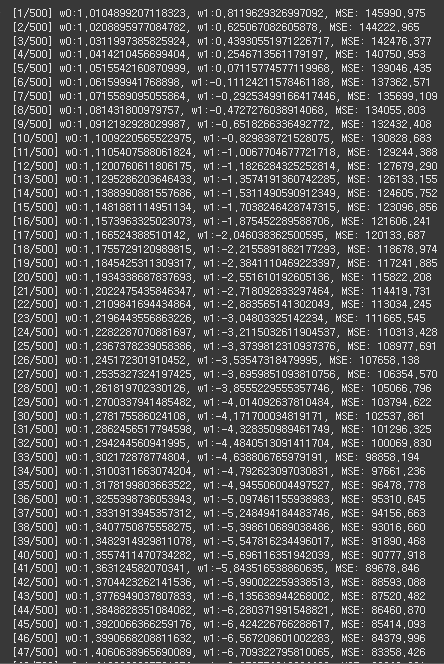
Function(MSE)점점 줄어드는 모습을 보면 학습이 잘 진행되고 있음을 알 수 있습니다.
이런경사하강법에는 크게 3가지 종류가 있습니다.
아카데믹한 경사하강법인 Batch Gradient Descent, 하나의 데이터만으로 진행하는 SGD(Stochastic Gradient Descent), Mini Batch형태로 데이터를 나누어 진행하는 Mini-Batch Gradient Descent가 있습니다.
1. Batch Gradient Descent
흔히 우리가 경사하강법이라고 하면 Batch Gradient Descent를 의미합니다.
Batch Gradient Descent는 모든 데이터셋에 경사하강법을 적용한다는 특징이 있습니다.
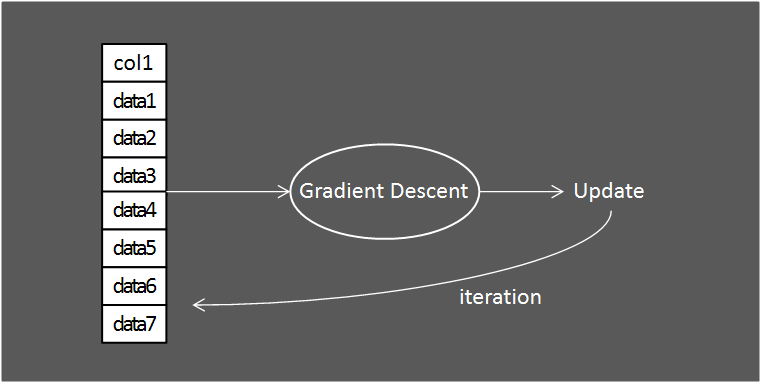
이렇게 학습하면 모든 데이터셋에 대해 학습을 진행하기 때문에 Model의 성능이 좋아질 수 있습니다.
하지만 저장공간, 컴퓨팅 비용 등 여러 문제로 인해 Batch Gradient Descent는 딥러닝에서 잘 사용하지 않습니다.
특히나, CNN에서 데이터 수는 기존 전형적인 데이터에 비해 기하급수적으로 많다는 걸 생각해보면 됩니다.
2. SGD(Stochastic Gradient Descent)
Batch Gradient Descent는 잘 사용하지 않는다고 했습니다.
이를 보완하기 위해 SGD(Stochastic Gradient Descent)라는 기법이 있습니다.
SGD는 하나의 데이터만 추출해 경사하강법을 적용하는 방식입니다.
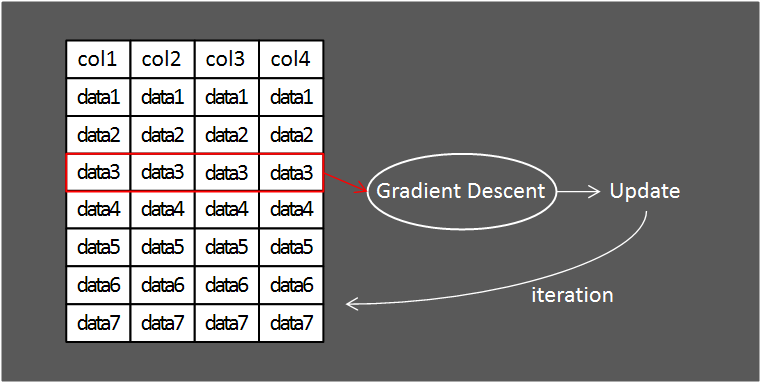
전체 데이터셋중 1개의 데이터만 가지고 와 학습하면 학습이 잘 이루어지지 않을 것 같지만 꼭 그렇지는 않습니다.
경사하강법에서 사용한 함수에서 SGD를 구현하고 성능을 파악하겠습니다.
import numpy as np
def true_function(X):
return 2*X[:,0] - 30*X[:,1]
def SGD_Gradient_Descent(X, Y, w0, w1, learning_rate=0.001):
idx = np.random.choice(100, 1)
N = X.shape[0]
prediction = w0*X[idx, 0] + w1*X[idx, 1]
diff = prediction - Y[idx]
w0_update = w0 - learning_rate*(2/N)*(np.dot(X[idx, 0].T, diff))
w1_update = w1 - learning_rate*(2/N)*(np.dot(X[idx, 1].T, diff))
return w0_update, w1_update
def SGD_iteration(X, Y, iter=1000, learning_rate=0.001):
w0 = 1
w1 = 1
global_minima_mse = 10**9
final_w0, final_w1 = 0, 0
for i in range(iter):
w0, w1 = SGD_Gradient_Descent(X, Y, w0, w1, learning_rate=learning_rate)
N = X.shape[0]
diff = w0*X[:, 0] + w1*X[:, 1] - Y
mse = np.mean(np.square(diff))
print('[{0}/{1}] w0:{2}, w1:{3}, MSE: {4:.3f}'.format(i+1, iter, w0, w1, mse))
if mse < global_minima_mse:
global_minima_mse = mse
final_w0 = w0
final_w1 = w1
return global_minima_mse, final_w0, final_w1
X = 12*np.random.randn(100,2)
Y = true_function(X)
global_minima_mse, final_w0, final_w1 = SGD_iteration(X, Y, iter=500, learning_rate=0.002)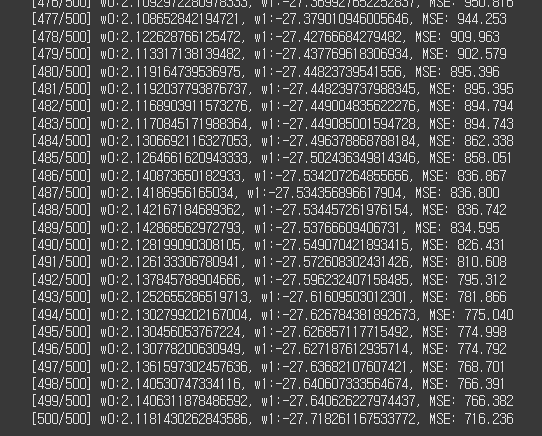
앞에서 언급은 안했지만 일반적인 GD를 적용했을 때 w0=2.1, w1=-29정도가 나왔습니다.
SGD를 적용했을 때는 w0=2.11로 2에 거의 근사했지만 w1=-27.71로 GD에 비해 조금 떨어진 성능을 보입니다.
하지만, 중요한 점은 전체 데이터에서 랜덤으로 1개만 선택했지만 성능의 떨어짐은 그에 비해 적었다는 점입니다.
3. Mini-Batch Gradient Descent
Mini-Batch Gradient Descent는 데이터를 특정 Batch Size로 나누어 그 데이터만큼 경사 하강법을 적용하는 방식입니다.
Batch Gradient Descent와 SGD의 사이 그 어디쯤이라고 생각하시면 될 것 같습니다.
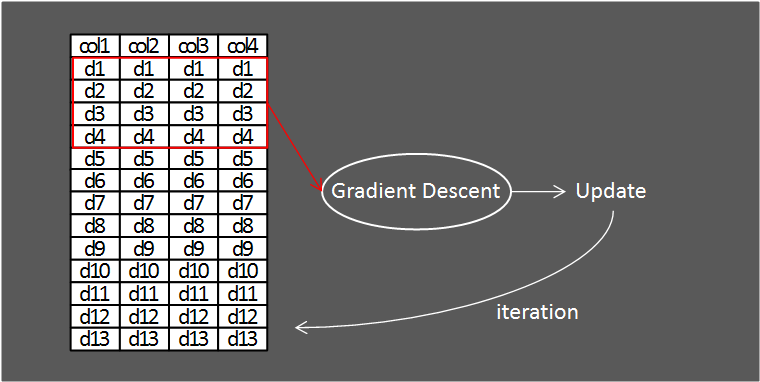
대부분의 딥러닝 프레임워크는 모델을 학습시킬 때 Mini-Batch Gradient Descent를 사용합니다.
하지만, 위 방법은 학습 시 성능의 문제때문에 조금 변형해서 사용합니다.
기존의 Mini-Batch Gradient Descent에서 Batch를 모든 데이터셋에 적용해 학습시키는 것입니다.
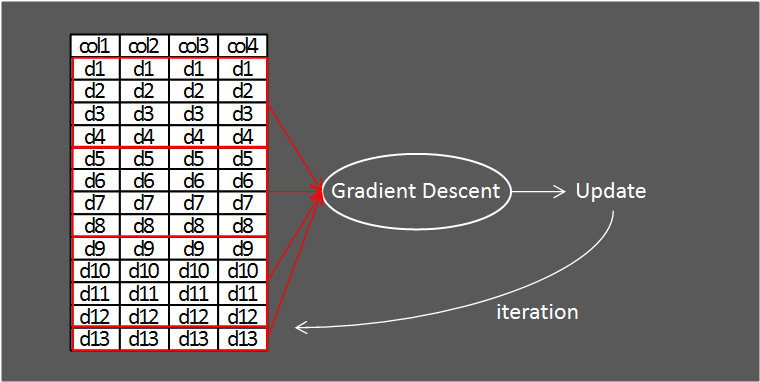
이렇게 각 Batch를 모두(위 그림의 경우 4번) 경사하강법을 적용시키면 한번의 iteration을 끝냈다고 표현합니다.
일반적인 딥러닝 프레임워크에서 사용하는 방식을 함수로 구현하며 이번 장을 마무리 하겠습니다.
import numpy as np
def true_function(X):
return 2*X[:,0] - 30*X[:,1]
def Mini_Batch_Gradient_Descent(X, Y, w0, w1, learning_rate=0.001):
N = X.shape[0]
prediction = w0*X[:, 0] + w1*X[:, 1]
diff = prediction - Y
w0_update = w0 - learning_rate*(2/N)*(np.dot(X[:, 0].T, diff))
w1_update = w1 - learning_rate*(2/N)*(np.dot(X[:, 1].T, diff))
return w0_update, w1_update
def Mini_Batch_iteration(X, Y, iter=1000, learning_rate=0.001, batch_size=30):
w0 = 1
w1 = 1
global_minima_mse = 10**9
final_w0, final_w1 = 0, 0
N = X.shape[0]
for i in range(iter):
for idx in range(0, N, batch_size):
w0, w1 = Mini_Batch_Gradient_Descent(X[idx:idx+batch_size, :], Y[idx:idx+batch_size], w0, w1, learning_rate=learning_rate)
diff = w0*X[:, 0] + w1*X[:, 1] - Y
mse = np.mean(np.square(diff))
print('[{0}/{1}] w0:{2}, w1:{3}, MSE: {4:.3f}'.format(i+1, iter, w0, w1, mse))
if mse < global_minima_mse:
global_minima_mse = mse
final_w0 = w0
final_w1 = w1
return global_minima_mse, final_w0, final_w1
X = 12*np.random.randn(100,2)
Y = true_function(X)
global_minima_mse, final_w0, final_w1 = Mini_Batch_iteration(X, Y, iter=500, learning_rate=0.00001)제가 이번 장에서 임의로 구현한 코드는 설명을 위해 회귀 함수를 true_function으로 사용했습니다.
실제로는 비선형 함수로 설명하기엔 경사하강법을 설명하기에 어려울 것 같아 임시로 설정했음을 알립니다.😁
