오늘은 퍼셉트론에 대해 공부하려고 합니다.
이게 참.. 공부하긴 했는데 퍼셉트론을 따로 빼서 작성하기엔 분량이 너무 적고, 그렇다고 다른 부분에 끼워넣기엔 동떨어진 느낌이 나서 그냥 "공부 기록을 작성하자"라는 의미에서 짧게 작성하려고 합니다.😊
📚 Perceptron (퍼셉트론)
퍼셉트론이란, 다수의 입력으로부터 하나의 결과를 도출하는 알고리즘입니다.
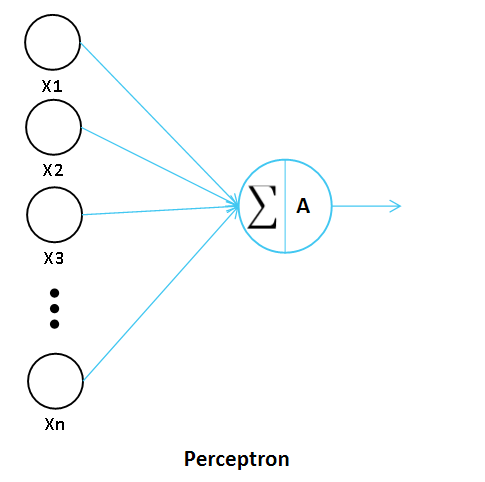
즉, 데이터를 입력받아 이를 가중치에 따라 계산한 후 Activation 함수를 거쳐 최종적으로 결과 값을 도출하는 알고리즘입니다.
앞서 회귀를 공부할 때도 다뤘지만, 회귀에서 최종적으로 모델이 찾고자 하는 것은 가중치 값입니다.
Neural Network에서도 마찬가지 입니다. 각 뉴런들은 가중치 값을 가지고 있으며, 최종적으로 가중치 값을 찾는 것을 목표로 합니다.
딥러닝에서도 경사하강법을 이용해 값을 직관적으로 도출하게 됩니다.
경사하강법 또한, 앞에서 공부했으니 참고하시기 바랍니다.
[ML] 회귀와 Gradient Descent(경사 하강법)
✅ MultiLayer Perceptron (다층 퍼셉트론, MLP)
앞에서 살펴본 그림은 단층 퍼셉트론입니다. 퍼셉트론이 한개라는 의미입니다.
퍼셉트론이 여러개 합쳐지면, 이를 다층 퍼셉트론이라고 부릅니다.
퍼셉트론 개념이 중요한 이유는 딥러닝의 기본 골격인 Neural Network가 단층 퍼셉트론으로 이루어진 다층 퍼셉트론이기 때문입니다.
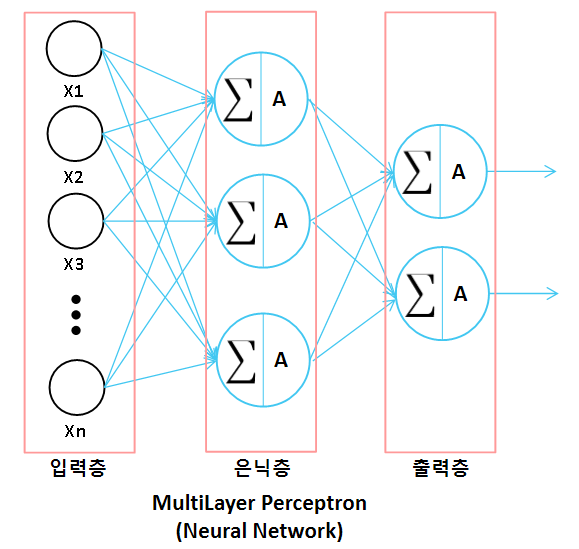
다층 퍼셉트론은 여러개의 Layer로 구성될 수 있습니다.
입력층, 은닉층, 출력층으로 나뉩니다.
- Input Layer(입력층): 데이터가 입력되는 Layer
- Hidden Layer(은닉층): 입력층과 출력층 사이에 있는 여러개의 Layer
- Ouput Layer(출력층): 최종 값을 반환하는 Layer
이중에서도 은닉층은 여러 층이 존재할 수 있는데, 이를 Deep Neural Network(심층 신경망)라고 부릅니다.
✅ Neuron (뉴런)
다층 퍼셉트론은 3가지 Layer가 있음을 알았습니다.
이때, 은닉층과 출력층에는 각 층을 연결해주는 뉴런이 존재합니다.
뉴런은 Net Input Function(순입력 함수)과 Activation Function(활성화 함수)로 구성됩니다.
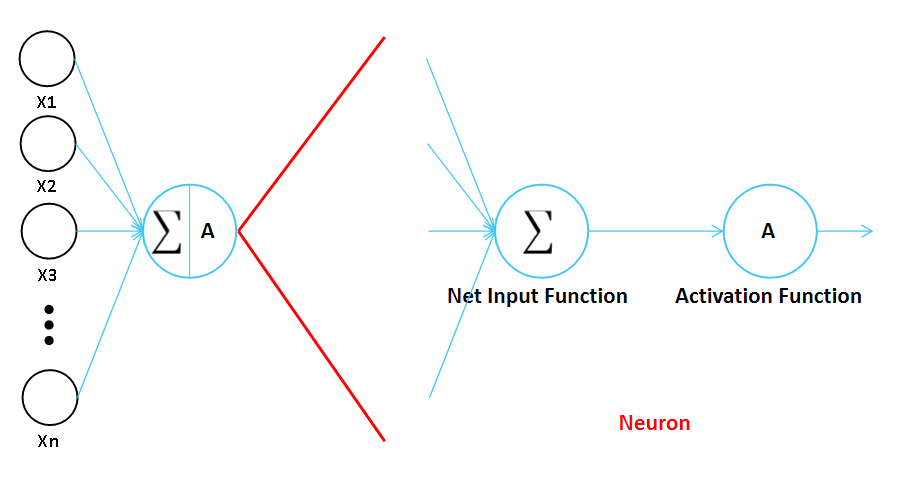
- Net Input Function: 입력값들과 가중치 값들의 곱을 하나의 신호로 표현하는 함수
- Activation Function: 입력 신호의 총합을 최종 출력 신호로 표현하는 함수
순입력 함수는 회귀에서와 마찬가지로 뉴런마다 연결된 가중치 곱의 합을 진행합니다.
여기까지는 회귀 모델과 완전히 동일하지만, 이렇게 출력된 값을 활성화 함수의 입력값으로 넣어줍니다.
활성화 함수는 일반적으로 비선형 함수를 사용하며, 활성화 함수를 사용함으로써 모델의 비선형성을 높여주게 됩니다.
여기서 활성화 함수까지 본격적으로 소개하진 않겠지만, 활성화 함수로는 로지스틱 회귀에서 봤던 Sigmoid, tanh, ReLU 등 다양한 종류가 있습니다.
활성화 함수에 대해서는 기회가 된다면 다뤄볼 예정입니다.
