Gradient Descent & Stochastic Gradient Descent

gradient descent

• sympy library를 사용한 gradient descent

import numpy as np
import sympy as sym
from sympy.abc import x 
from sympy.plotting import plot

def func(val):
    fun = sym.poly(x**2 + 2*x + 3)
    return fun.subs(x, val), fun  #fun(x)에 val 대입한 값(== y값), fun함수식 반환, val == x값

def func_gradient(fun, val):
    ## TODO
    diff =  sym.diff(fun(val)[1]) #도함수
    return diff.subs(x, val), diff  #diff(x)에 val 대입한 값(==기울기), 도함수 반환

def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5):
    cnt = 0
    val = init_point  #초기값
    grad = func_gradient(fun,val)[0]  #초기값에서의 기울기
    ## Todo
    while abs(grad) > epsilon: #epsilon 보다 작으면 종료
        val = val - lr_rate * grad  #val값 update
        grad = func_gradient(fun,val)[0]  #update된 val값의 기울기 계산
        cnt += 1
    print("함수: {}\n연산횟수: {}\n최소점: ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))  #(x값,y값)

• 결과
  

• sympy를 사용하지 않고 직접 구현한 gradient descent

def func(val):
    fun = sym.poly(x**2 + 2*x + 3)
    return fun.subs(x, val)

def difference_quotient(f, x, h=1e-9):
    ## Todo
    result = (f(x+h) - f(x-h)) / (2*h)  #미분식 (f(x+h) - f(x))/h)를 사용해도 상관없음
    return result

def gradient_descent(func, init_point, lr_rate=1e-2, epsilon=1e-5):
    cnt = 0
    val = init_point
    grad = difference_quotient(func,init_point)
    ## Todo
    while abs(grad) > epsilon: #epsilon 보다 작으면 종료
        val = val - lr_rate * grad  #val값 update
        grad = difference_quotient(func,val)  #update된 val값의 기울기 계산
        cnt += 1
    print("연산횟수: {}\n최소점: ({}, {})".format(cnt, val, func(val)))

• 결과
  

Stochastic Gradient Descent

train_x = (np.random.rand(1000) - 0.5) * 10
train_y = np.zeros_like(train_x)

def func(val):
    fun = sym.poly(7*x + 2)
    return fun.subs(x, val)

for i in range(1000):
    train_y[i] = func(train_x[i])

# initialize
w, b = 0.0, 0.0

lr_rate = 1e-2
n_data = 10
errors = []

for i in range(100):
    ## Todo
    #mini_batch 생성
    idx = np.random.choice(1000, 10, replace=False) #replace : 중복 허용x
    mini_x = train_x[idx]
    mini_y = train_y[idx]

    #예측
    pred_y = w * mini_x + b

    #오차(생략,미분식에 바로 대입)

    #미분
    gradient_w = (2/n_data) * np.sum((mini_y - pred_y)*(-mini_x))
    gradient_b = (2/n_data) * np.sum(-(mini_y - pred_y))

    #값 업데이트
    w = w - lr_rate * gradient_w  #학습률을 곱해 기존의 값을 업데이트
    b = b - lr_rate * gradient_b


    error = np.sum((mini_y - pred_y)**2)/n_data #MSE (평균제곱오차) : (정답과의 거리를 통해서 성능측정)
    # Error graph 출력하기 위한 부분
    errors.append(error)

print("w : {} / b : {} / error : {}".format(w, b, error))

• 결과
  

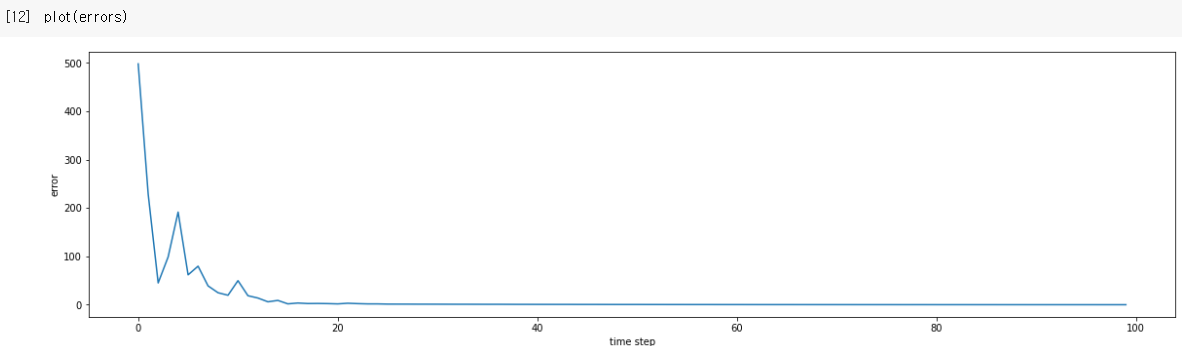
• 시각화