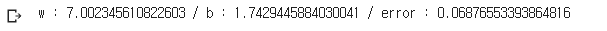Linear Regression

Linear Regression

1. 예측
2. 정답과의 오차 측정
3. 미분
4. 값 업데이트

train_x = (np.random.rand(1000) - 0.5) * 10
train_y = np.zeros_like(train_x)  #정답

def func(val):
    fun = sym.poly(7*x + 2)
    return fun.subs(x, val)

for i in range(1000):
    train_y[i] = func(train_x[i])

# initialize
w, b = 0.0, 0.0

lr_rate = 1e-2
n_data = len(train_x)
errors = []

for i in range(100):  #epoch = 100
    ## Todo
    # y예측
    pred_y = w * train_x + b  # pred_y에 w와b가 대입된 예측값이 들어감  ####
    
    # 오차(생략, 미분식에 바로 대입)
    
    # gradient : w와b를 구하는것이 목적이므로 w와b로 편미분
    gradient_w = (2/n_data) * np.sum((train_y - pred_y)*(-train_x))
    gradient_b = (2/n_data) * np.sum(-(train_y - pred_y))

    #학습률을 곱해 기존의 값(w,b)을 업데이트
    w = w - lr_rate * gradient_w  #학습률을 곱해 기존의 값을 업데이트
    b = b - lr_rate * gradient_b

    # error를 시각화 하기위해 MSE 정의
    error = np.sum((train_y - pred_y)**2)/n_data #MSE (평균제곱오차) : (정답과의 거리를 통해서 성능측정)

    # Error graph 출력하기 위한 부분
    errors.append(error)

print("w : {} / b : {} / error : {}".format(w, b, error))

• 결과
  

• 시각화

from IPython.display import clear_output
import matplotlib.pyplot as plt
%matplotlib inline

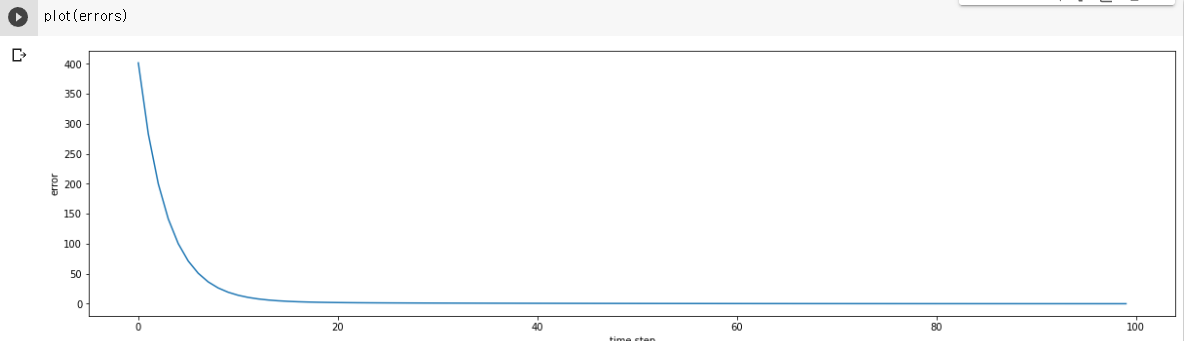
def plot(errors):
    clear_output(True)
    plt.figure(figsize=(20,5))
    plt.ylabel('error')
    plt.xlabel('time step')
    plt.plot(errors)
    plt.show()

• 결과
  

조금 더 복잡한 선형식에 대한 Regression

$y = w_0x_0 + w_1x_1 + w_2x_2 + b$
$y = x_0 + 3x_1 + 5x_2 + 7$

train_x = np.array([[1,1,1], [1,1,2], [1,2,2], [2,2,3], [2,3,3], [1,2,3]])
train_y = np.dot(train_x, np.array([1,3,5])) + 7  #두번째 식 y값
print(np.shape(train_y))
# random initialize
beta_gd = [9.4, 10.6, -3.7, -1.2]
# for constant element
expand_x = np.array([np.append(x, [1]) for x in train_x]) #각 element에 상수항 추가

for t in range(5000):
    ## Todo
    #예측
    pred_y = np.dot(expand_x,beta_gd)
    #정답과의 오차 측정
    error = train_y - pred_y
    #미분 : expand_x 는 (6,4) error는 (6,)이므로 expand를 transpose시켜야 내적 가능
    grad = -np.dot(np.transpose(expand_x),error)
    #값 업데이트  (lr_rate = 0.01)      # @
    beta_gd = beta_gd - 0.01 * grad

print("After gradient descent, beta_gd : {}".format(beta_gd))

• 결과